流动空气压差比拟与风电叶片翼型线确定理论的探讨

张维恩，王娅萱，张淼淼，吴 彤，刘舒萱

（北京工业大学 环境与能源工程学院，北京 100124）

1 研究背景

文献[1]研究发现，目前，风力发电叶片翼型基本沿用航空器翼型，尽管根据风力发电叶片自身工况研制出了一些风电叶片翼型，但这些所谓的风电叶片专用翼型仍以探索为主，在流动空气与叶片相互作用规律的认识及以这种认识为基础的风电叶片翼型理论尚须进行更深入的研究工作。风力发电叶片就是其翼型沿风轮径向的分布，因此，翼型影响着流动空气与风电叶片的相互作用，也就影响着风电叶片捕获风能的能力，所以研究风电叶片翼型线设计理论就是研究流动空气与风电叶片的相互作用规律。常见的风电叶片翼型主要有三种表达方法：形函数扰动法、外形参数化方法[2]和解析函数法。形函数扰动法是在原始翼型基础上添加扰动形函数进行线性叠加而产生翼型的方法[3]，形函数较多采用Hicks-Henne函数[4]，但此种方法对原始翼型依赖性强。外形参数化法是用数个参数描述翼型各个部位的几何尺寸，设计变量的几何意义明确，但难以用解析式表达[5]。解析函数法是用函数式直接表示翼型，如早期用多项式表达的NACA 4位数、5位数系列翼型等。目前仍有学者对翼型进行较深入的研究工作，文献[6]提出了一种基于Trajkovski共形变换理论的风力发电翼型的广义函数，此函数可用于拟合现有的翼型型线，可通过调整广义函数系数创建新的翼型型线，并以FX66-S196-V1翼型为例，通过选取适当的拟合项数，求解出了其解析式，为风力发电专用翼型设计理论和方法的研究拓宽了思路；文献[7-9]分别基于保角变换、儒可夫斯基翼型变换和西奥道生法，提出了翼型型线的集成设计理论及方法，推导出了能够广泛应用的翼型集成的级数表达形式；文献[10]提出了一种设计大型风力发电叶片翼型系列的集成方法。对于给定的转子直径和叶尖速比，基于局部速度比设计最佳翼型。文献[11]基于梯度算法、XFOIL代码以及与贝塞尔曲线的原始参数化相结合描述翼型，结果表明新翼型与现有候选翼型相比具有更好的气动性能和控制性能；文献[12]根据一种演化算法优化工具链接到几何模块以生成翼型的几何形状；文献[13]提出了一种基于翼型积分表达式和B样条曲线设计出了两种具有相似厚度的新翼型；Yiu等[14]利用流逸技术和最小二乘法设计翼型；Shenoy[15]结合优化算法和流程代码以及实施一次性方法解决最佳翼型设计问题；Thinakaran[17]使用人工神经网络（ANN）研究了翼型的反设计方法，测试表明该方法可以准确地预测翼型型线[16]；SOBIECZKY提出可通过控制翼型几何参数来设计现代翼型，并命名为PARSEC翼型设计法。文献[18]通过研究流动空气与风力发电叶片的相互作用分别提出了风力发电叶片迎风面流出角的确定理论和相应公式及流动空气从风力发电叶片背风面后缘流出角的确定理论和相应公式，文献[19]还给出风力发电风轮出力的计算公式。对已有翼型设计的研究发现：领域学者非常重视研究风电叶片翼型，但研究方法基本以翼型优化或对已有翼型变量取值的优化提高风力发电叶片的气动性能为主；而研究流动空气与风电叶片的相互作用，提出并建立风电叶片翼型线设计理论并进行应用的研究，在公开资料中尚未看到。为此，我们认真观察了流动空气吹向风电叶片，尤其是与风电叶片前缘接触瞬时状态的变化及沿风电叶片表面的流动情况，提出并建立了风力发电叶片翼型线设计理论并进行了相应研究，导出了根据流动空气压差比拟确定的风电叶片翼型线理论公式。

2 流动空气的压差比拟

风将空气吹向风电叶片迎风面，当其触碰到叶片相应处的翼型线时，该空气将沿此翼型线的切线方向向风电叶片尾缘运动，见图1所示。容易理解，此空气是在其前后空气压差的作用下流动的。因为，流动空气的空气压差难以精确测量，且不同风速流动的空气前后压差也不相同，但总存在某个常数C，其流动的空气压差等于或近似等于该流动空气质点的重量△mg（其中，△m为该空气质点的质量，g为重力加速度）与该常数C的乘积。忽略空气及空气与风电叶片间的摩擦，则，可将此空气质点在其前后空气压差作用下沿翼型线的流动看成是在真空条件下，在其重力作用下沿相应翼型线的运动。此即流动空气的压差比拟。

图1 流动空气与风电叶片迎风面翼型线作用模型

3 压差比拟条件下的空气运动能量转换

流动空气触碰到风电叶片时，由于叶片的节流效应，将促使空气流动速度加快，亦即，在空气压差的作用下，空气将由其接触到的风电叶片前缘向后缘快速流动，此过程中，该空气质点前后压差沿风电叶片翼型线做的功将转化为其动能增加量。

在这里，功Es转化为了空气质点运动的动能E，包括沿矢径运动的动能和绕坐标原点转动的动能，则

式中：v为空气质点沿矢径运动的速度；ω为空气质点绕坐标原点转动的角速度。

根据上述分析，有

此即压差比拟条件下空气运动能量的转换关系式。

4 风电叶片翼型线确定理论

其中q介于r′与p之间，而p为极值曲线场中极值曲线的斜率，其它符号意义同前。

即勒让德条件满足勒让德强条件，则式（11）为极大值曲线方程，说明空气质点由风电叶片前缘运动到后缘所需要的时间较长，即在任一瞬时，作用在风电叶片翼型线上的空气质点与翼型线上的对应点都有着较强作用，从而使风电叶片具有较强捕风能力。

5 风电叶片新翼型线确定理论的验证和评价

为验证式（11）给出的翼型线的正确性，从翼型库中选取翼型几何参数与式（11）给出的翼型弦长相等、最大相对厚度相差2.896%的BRUXEL36翼型，见图2（a）所示，图2（b）即为式（11）确定的风电叶片新翼型。

图2 风电叶片新翼型(b)和对比翼型(a）

利用Xfoil软件，分别计算出两种翼型的升力系数Cl和阻力系数Cd随攻角alpha的变化关系曲线，如图3所示。从图3可以看出，攻角在-2°～6°范围内，风电叶片新翼型的升力系数明显高于BRUXEL36翼型的升力系数，同时，风电叶片新翼型的阻力系数明显低于BRUXEL36翼型的阻力系数。软件给出的两种翼型的升阻比见图4所示，从图4可以看出，风电叶片新翼型在-2°～6°的攻角范围内拥有较高的升阻比，其中在攻角alpha=3°时，新翼型升阻比高出BRUXEL36翼型25左右。由此可见，在攻角alpha=-2°～6°工况下，选择风电叶片新翼型比BRUXEL36翼型具有更好的风能转化率和利用率，尤其在攻角alpha=3°时，新翼型具有更好的优越性能。

图3 风电叶片新翼型和对比翼型升阻力系数随攻角的变化关系曲线

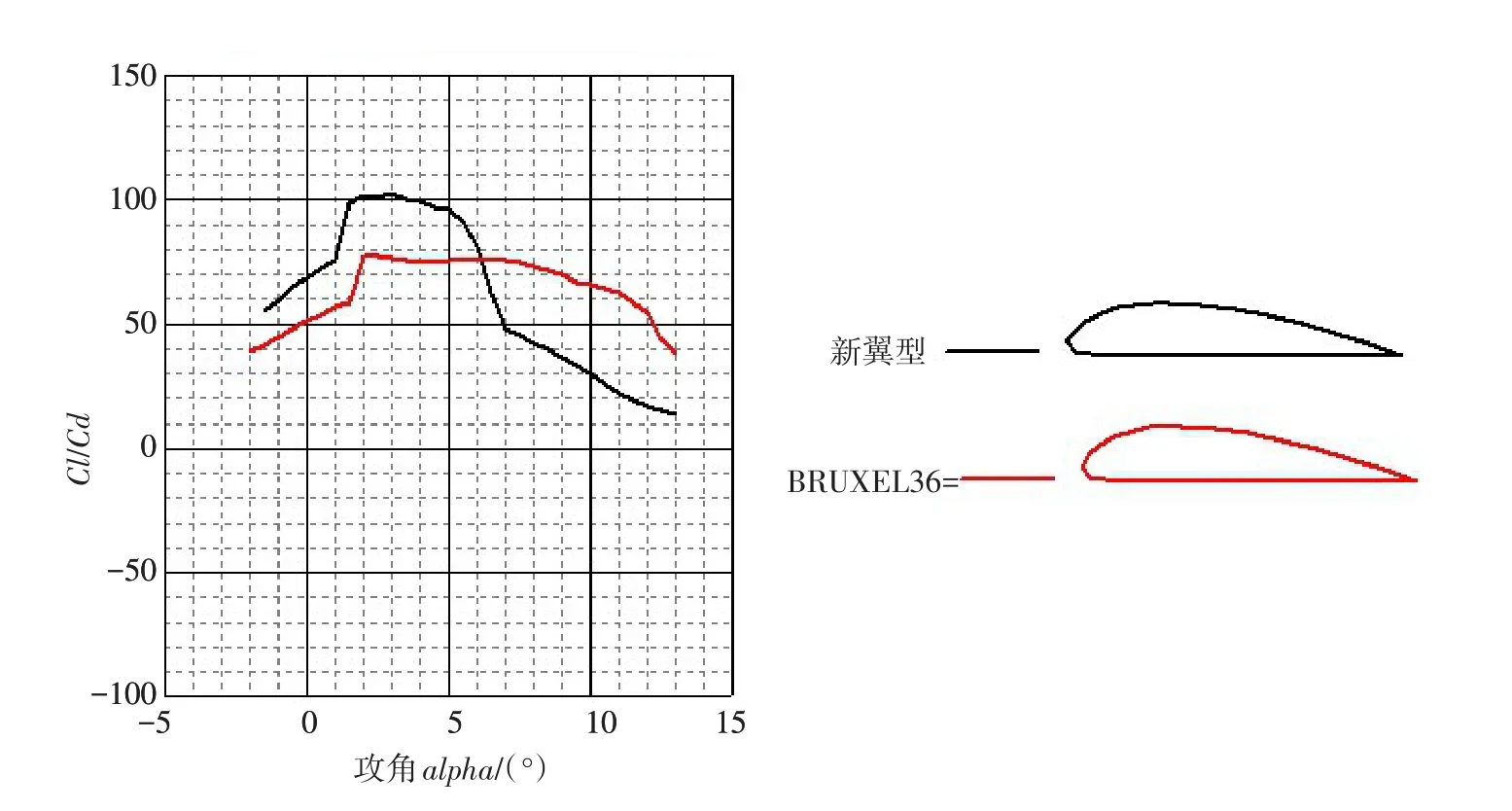
图4 风电叶片新翼型和对比翼型升阻比随攻角的变化关系曲线

6 结论与讨论

目前，风电叶片翼型线的设计基本借用航空翼型或借鉴航空翼型的设计方法，因此，论文通过对流动空气与风电叶片相互作用的研究及根据这样研究设计风电叶片翼型线的理论在领域内是非常有益的新尝试和发展。将论文理论设计的新翼型与翼型库中相似翼型BRUXEL36通过Xfoil软件对比研究发现：（1）新翼型在攻角-2°～6°范围内，升力系数明显高于对比翼型BRUXEL36，而阻力系数明显低于对比翼型BRUXEL36；（2）新翼型在攻角-2°～6°范围内，升阻比明显高于对比翼型BRUX⁃EL36，尤其在3°攻角时，新翼型升阻比高出BRUXEL36翼型25左右。因此，新翼型在攻角-2°～6°工况下，优于与之相似的对比翼型BRUXEL36。