基于自适应蒙特卡洛法评定测量不确定度程序开发与应用

王高俊，黄河清，章明洪

(1.上海化工院检测有限公司，上海 200062； 2.上海化工研究院有限公司，上海 200062）

社会生活的很多方面需要化学分析及其结果，例如贸易结算中商品的有效成分含量是否达标，环境检测中关注的污染物是否超标，化学品的安全性能是否达标或具有何种危险性等。化学分析结果质量的高低，往往对生产和生活产生较为重大的影响。在分析化学中，过去常以误差或精密度作为测量结果质量的表征，误差是指测量结果与被测量的真值之间的差值，但是使用误差对测量结果的质量进行评价存在普遍的局限性，因为真值往往是不可知的；精密度指按照规定方法进行分析得到的测量结果的分散性，其要求必须按照统一的“官方”方法进行测量，且其不能反映测量结果的置信度，因此使用精密度对测量结果进行质量评价，也存在局限性。现代化学分析领域，测量不确定度常常被用来表征测量结果的可信度。

测量不确定度表征了被测量的真值所处量值的范围，通常采用95%的概率下，被测量真值落在被测量结果附近的范围。测量不确定度评定的经典方法为GUM 法，此方法由ISO 于1993 年提出［1］。GUM 法将测量不确定度的来源分为A、B 两类，基于不确定度传播理论，通过分析测量不确定度的来源，进行计算合成，最终得到测量不确定的评定结果。但是此方法存在一些难以解决的问题，如复杂模型中不确定度传播的计算难以进行、不确定度来源的重复计算和遗漏等。为了解决这些问题，有人提出采用蒙特卡洛法进行测量不确定度的评定。我国的JJF1059.2-2012《用蒙特卡洛法评定测量不确定度》对蒙特卡洛法进行测量不确定度的评定进行了详细的规定和说明［2］。

自适应蒙特卡洛法评定测量不确定度，其主要优势在于有效地解决了传统评定方法中高阶项展开困难、不确定度信息遗漏或重复计算等问题。自适应蒙特卡洛法评定测量不确定度在测量领域已经得到了一定的应用［3-15］。采用自适应蒙特卡洛法评定测量不确定度，需要对测量模型进行多次“海量”数值模拟采样，通常需要采用计算机编程的方式进行大量计算，因此该方法的推广存在一定的难度。现有用于蒙特卡洛法进行测量不确定度评定的计算分析软件，存在不支持自适应计算［16］、支持独立分量较少［17］、不支持过程变量和自定义变量名称［18-19］等问题。笔者基于Python 语言，设计了自适应蒙特卡洛法进行测量不确定度评定的计算分析程序，为该方法提供更为高效便捷的工具。

1 程序设计框架

设计的自适应蒙特卡洛法评定测量不确定度，主要分为5 个阶段，其测试步骤如图1 所示。

（1）输入阶段。确定被测量与输入量，输入数学模型，输入独立变量的概率分布情况。首先需建立被测量的数学模型，并将数学模型中的输入量分解至独立变量。较为复杂的数学模型，需经过多层分解，才能使输入量成为独立变量。

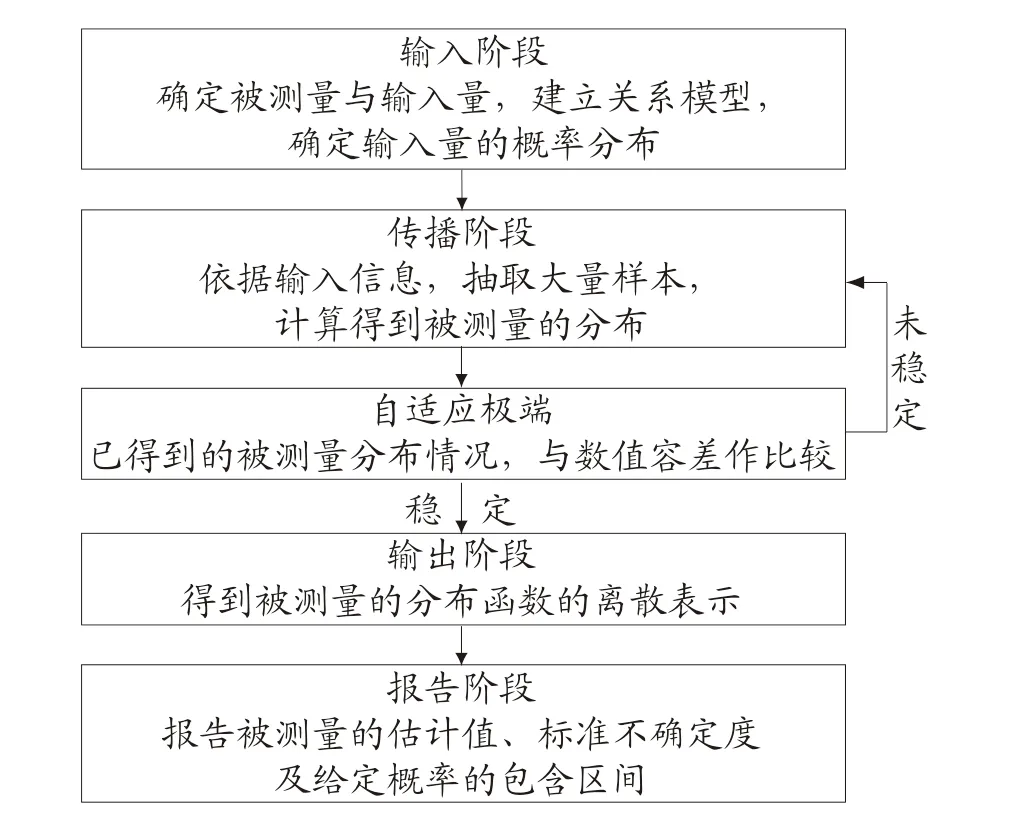
图1 自适应蒙特卡洛法评定测量不确定流程图

例如化学分析中常见的使用分析仪器进行定量的测量过程，被测量通常为目标物质的浓度cy，其数学模型通常按照式(1)计算：

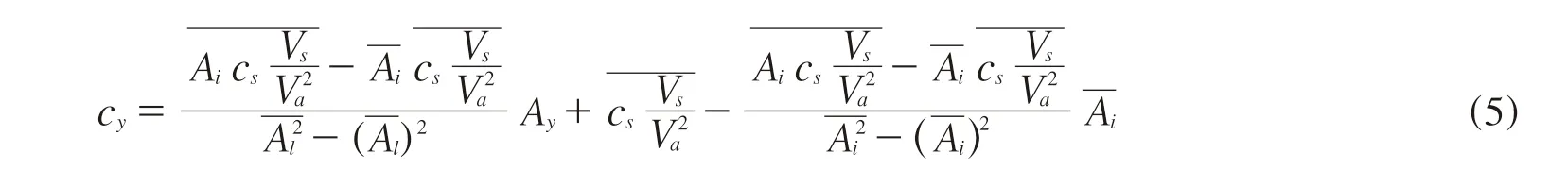
现有的一些采用蒙特卡洛法评定测量不确定度的软件，通常要求对被测量的数学模型进行一次性输入，即输入上文中的数学模型ci。复杂的数学模型，不仅会增加输入错误的可能性，同时降低了模型的可读性。因此，本程序引入了过程参数的设计，降低被测量数学模型的复杂度，以提高模型的可读性与易用性。

（2）传播阶段。依据输入信息，抽取大量样本，计算得到被测量的分布。通过对独立变量进行数值模拟，测量不确定度由独立变量传递至过程参数，进一步传递给被测量，进而完成测量不确定度的传播。

（3）自适应阶段。依据已得到的被测量分布情况，与数值容差做比较，若被测量未稳定，则返回传播阶段，继续采样，直至被测量分布稳定。每轮采样次数及数值容差，依据JJF 1059.2-2012 《用蒙特卡洛法评定测量不确定度》进行设计，每轮采样次数默认设置为10 000 次。

（4）输出阶段。将采样阶段得到的所有被测量进行排序，得到其分布函数的离散表示。

（5）报告阶段。报告被测量的平均值及测量不确定度。

2 界面设计

自适应蒙特卡洛法评定测量不确定度的程序由Python 语言编写，打包转为exe 程序，方便使用，亦可通过Python 编译器直接对源文件进行使用。程 序 已 开 源 至github.com／kiddog99／Adaptive_MCM_workspace。程序的界面如图2 所示。

图2 自适应蒙特卡洛法评定测量不确定度程序界面

3 应用示例

以CNAS-GL006: 2019 《化学分析中不确定度的评估指南》中的例子A2 为例，说明本软件的应用方法。例中，使用邻苯二甲酸氢钾标准物质对氢氧化钠溶液进行标定。其中，被测量为氢氧化钠的浓度cNaOH，其终点数学模型为式(6)：

模型需要进一步分解至独立变量，其中过程模型：（1）m(KHP)通过差减称量获得，即m(KHP)=m(KHP1)-m(KHP2)；（2）m(KHP)的计算包含分子式里4 种不同元素，即m(KHP)=M(C8)+M(H5)+M(O4)+M(K)；（3）V取决于温度和测量系统的校准，即V=V(T) (1+αdT)。

本测量过程涉及的独立变量共10 个，列于表1。程序使用界面如图3 所示，右侧为输入内容展示界面，由上至下分别为终点数学模型、过程参数模型、独立变量。其中，过程参数模型显示框中，内容包括过程参数名称[如m(KHP)]，计算过程[如m(KHP1)-m(KHP2)]，以及包含的独立变量[如m(KHP1)、m(KHP2)]。独立变量显示框中，内容包括独立变量名称、分布方式及其关联的过程参数。将终点数学模型、过程参数模型、独立变量分别输入自适应蒙特卡洛法评定测量不确定度的程序，即可点击“自动采样”按钮，得到模拟计算结果。

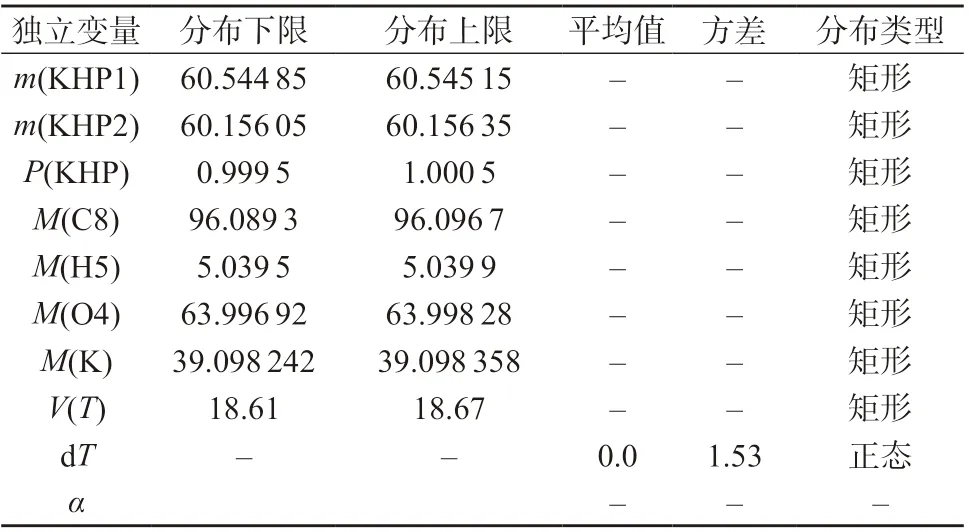
表1 氢氧化钠的浓度数学模型中的独立变量

如图3 所示，以NaOH 溶液浓度的计算为例，点击“开始采样”按钮，程序开始数值模拟采样，并经过自适应算法，达到数值稳定后，输出计算结果。采样结果中，被测量c(NaOH)的平均值为0.102 1，标 准 偏 差 为0.000 1，95% 置 信 区 间 为［0.102 0，0.102 3］。此输出结果与CNAS-GL 006: 2019 《化学分析中不确定度的评估指南》中给出的参考结果一致，可以认为程序的自适应蒙特卡洛法模拟计算在本例中是准确的。

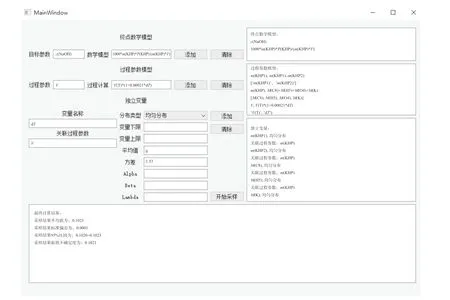
图3 程序使用界面及计算结果

4 结果与讨论

基于Python 语言开发的自适应蒙特卡洛法评定测量不确定度程序，界面简洁，操作简单，计算准确，适用于任意多个独立变量、任意多个过程参数及单一被测量的数学模型。其中，过程参数的设计，与蒙特卡洛法对被测量数学模型的分解思路相适应，降低了被测量数学模型的复杂度，提高了模型的可读性与程序的易用性。自适应蒙特卡洛法评定测量不确定度计算程序的开发，可以有效地降低使用自适应蒙特卡洛法进行测量不确定评定的难度，相关的从业人员，不需要具备专业的编程知识，即可使用该软件快速简易地进行测量不确定度的评定。这有利于从业人员提高对化学分析结果的认识，提高我国化学分析行业的整体水平。

同时，应该意识到，自适应蒙特卡洛法，利用足够大量的数值模拟采样，达到获取被测量真实分布情况。因此，自适应蒙特卡洛法每次进行模拟采样，均存在随机性。具体而言，每次采样，每个独立变量的数值均由random 模块依据变量的分布概率密度生成。这导致自适应蒙特卡洛法的评定结果总会有轻微的偏差，即评定结果无法再现，这也是自适应蒙特卡洛法评定测量不确定度程序的优化方向。