含分布式电源配电网的智能故障诊断方法
2021-01-25陈佳慧靳一玮
陈佳慧,靳一玮
(上海电力大学 电子与信息工程学院,上海 201306)
1 概述
近年来,随着分布式发电技术的发展,含分布式电源配电网的故障诊断技术也受到了各界的关注,成为分布式电源配电网发展不可或缺的重要核心技术之一,可及时精确处理电网故障、确保其稳定运行。
目前,人工智能方法被广泛用于电网故障诊断研究中,使得故障诊断的速度和精度得到了不断地改善[1-2]。刘科研等[1]采用支持向量机法对有源配电网进行故障分类和定位,得到了较高的故障分类精度;孙洁娣等[2]利用卷积神经网络和长短期记忆网络(Long Short-Term Memory networks,LSTM)实现了智能和可靠的轴承故障诊断。其他研究还会同时利用小波变换对信号进行特征提取,它可对信号进行时频分析,能较好地处理暂态和噪声等信号。
本文采用了最大重叠离散小波变换(Maximum overlap discrete wavelet transform,MODWT)和 LSTM 神经网络进行故障诊断,其中,LSTM 网络在预测时间序列和故障诊断等方面有应用,它可以较好地处理时序数据,利用状态的时间序列来学习故障信息[2];MODWT 变换是一种高度冗余的非正交变换,它能较快地检测瞬态,对起始点的选择没有要求,还能处理任何长度的信号,适用于分析故障检测等问题[3-4]。因此,文中考虑了LSTM 网络能较好分析时序数据和MODWT 变换具备快速检测暂态等特点,将两者应用到含分布式电源配电网中,旨在提高故障检测和分类的准确率。
2 故障诊断方案
文章主要研究将MODWT 变换和LSTM 网络结合应用到含分布式电源配电网的输电线路短路故障诊断中。具体的故障诊断方案如下:(1)通过SIMULINK 搭建相应的含分布式电源配电网模型,并获取数据。(2)进行故障检测。对电流信号进行MODWT 变换,通过分析小波的第一级细节系数可以判别是否发生故障,若发生故障还需要检测出故障发生时刻。(3)进行特征提取。选取故障发生前后1 个工频周期的 A、B、C 三相电流 IA、IB、IC以及零序电流分量 IC作为特征提取的对象,并计算相应的特征向量。(4)进行网络训练、测试。将(3)中得到的特征向量输入到搭建好的神经网络模型中进行训练和测试,得到故障分类结果。
2.1 模型的建立和数据的产生
为评估文中所提方法的性能,通过MATLAB 软件搭建修正的IEEE13 总线标准系统模型进行算例分析[5],如图1所示。以下是对该系统的一些说明:
(1)这是一个小型、高负载且三相不平衡的4.16kV馈线系统。(2)原系统的节点650 和节点632 通过稳压器连接,此系统将4.16kV 的三相电压源直连节点632。(3)一个4.16kV/480V 的变压器将光伏发电单元连接到节点680,从而实现并网。(4)不改变系统其他数据,具体参数参考文献[5]。
文中考虑了随机的故障发生时刻、故障发生线路、过渡电阻和短路故障类型等不同影响因素下的故障工况,具体设置如下:(1)故障发生时刻:故障发生的时刻具有随机性,在[0,0.5s]上服从均匀分布,仿真过程中设置了三个故障发生时刻分别为 t1、t2、t3。(2)可能发生故障线路:line632-633、line632-671、line671-680。(3)过渡电阻:0.01、1、10。(4)短 路 故 障 类 型 :AG、BG、CG、AB、AC, BC、ABC、ABCG、ABG、ACG、BCG。共产生3*3*3*11=297 种故障工况。
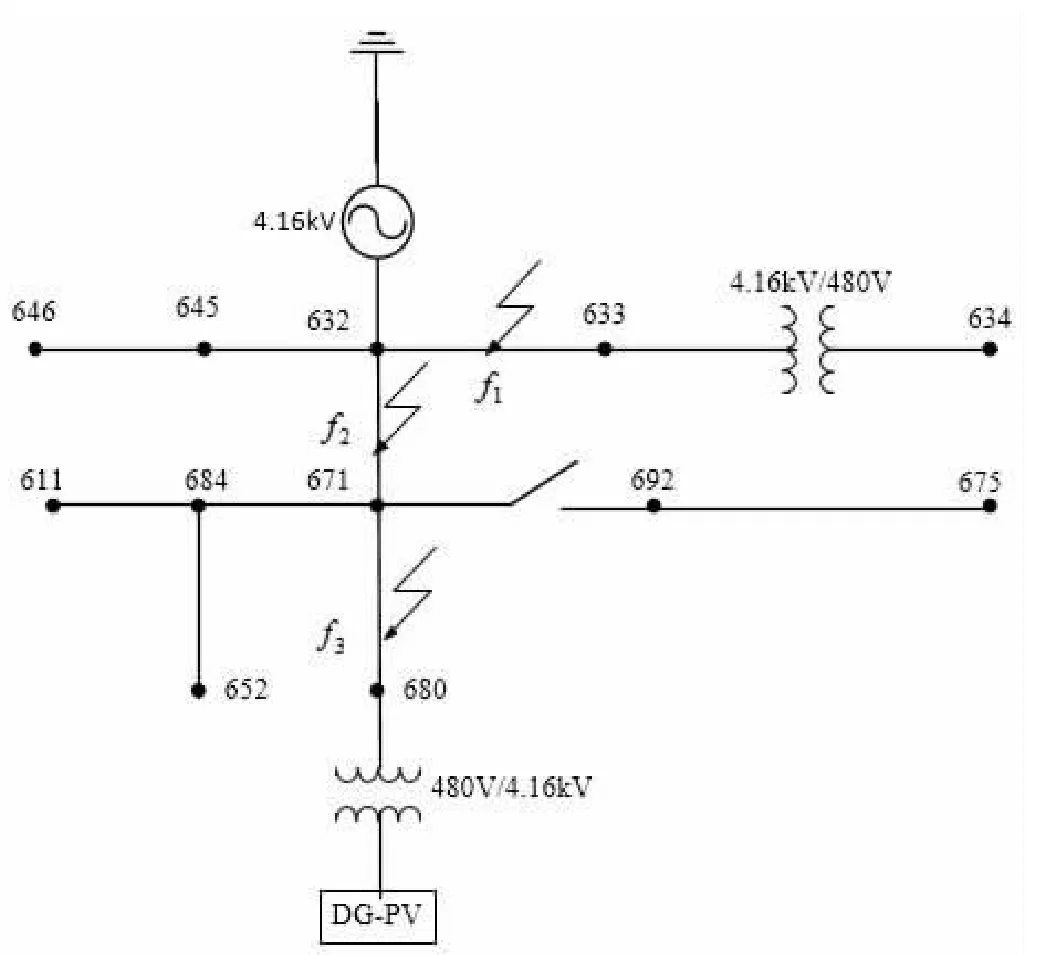
图1 修正的IEEE13 总线标准系统图
2.2 故障检测
2.2.1 MODWT 变换理论简介
MODWT 变换具备以下几个特点[3-4]:它对所处理的信号长度没有要求,因此适用范围广;它没有降采样过程,可以在每个采样过程之后立即计算小波系数;同时,它对时间序列的起始点没有要求,可以任意选择。这些特点使得MODWT 变换相对于DWT 变换分析暂态信号时更具优势,尤其适合于分析具有任意故障初相角的故障检测和分类问题。
MODWT 变换将信号 Y(N)分解成 log2N 级,其中,N 为信号的长度。另外,MODWT 变换的细节系数和尺度系数的公式[5]分别为
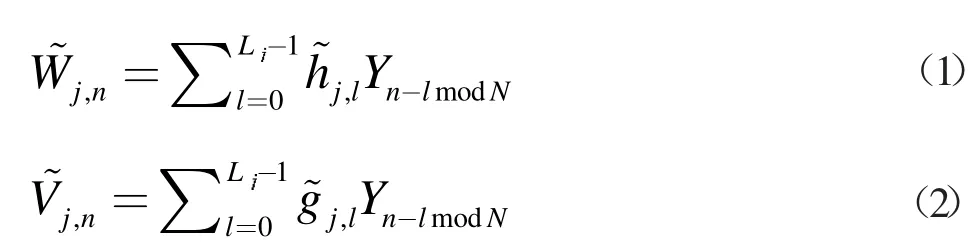
式中,N 为信号的长度;l=0,1,2,...L-1;L 为滤波器的宽度为第 j 级的尺度滤波器为第 j 级的小波滤波器。
2.2.2 检测算法
故障检测算法的作用是判断是否发生故障,同时,若发生故障则还需检测出故障的发生时刻。当得到数据后,首先需要进行故障检测来判断是否发生故障,若发生故障,电流将发生突变,并产生短暂的瞬态现象。通过提取、分析MODWT 变换第一级系数的高频分量,可检测到故障发生时刻,否则检测结束。相关研究提出了利用阈值法来检测故障[6],即对电流进行小波变换,再提取、分析第一级小波细节系数,若系数超过设置的阈值,则可以检测是否发生故障并确定故障发生时刻。然而,此方法存在难以选择合适阈值的问题,若阈值设置不当,可能会出现漏检或误检等现象。为了避免及提高检测率,本文提出基于信号本身幅值大小的阈值选取方法,即基于相邻系数差的阈值法,而不是常规的经验法。具体的故障检测算法如下:(1)使用“Haar”小波对电压进行 MODWT 变换;(2)提取每相的第一级细节系数,并去除前1000 个和最后1000 个细节系数;(3)计算并确定基于相邻系数差的阈值。对于(2)中获得的系数,首先计算出相邻点之间系数差的绝对值Dk,如公式(3)所示。接着进行比较,并找到最大值Dkmax及其所在相,设定的阈值即为Dkmax,

(4)将Dkmax所在相的细节系数绝对值与阈值进行比较,若首次出现大于阈值的,则对应的为故障发生时刻。
以发生C 相接地短路(CG)为例,图2 为使用基于相邻系数差的阈值法检测CG 故障发生时刻的结果图。
由图2 可以看出,采用文中的故障检测算法可以精准地检测出故障的发生时刻,并且不存在延时现象,至于故障检测的识别率,将和故障分类的准确率一起讨论,详见3 中的结果与分析。
2.3 特征提取
特征提取的目的是选择合适的特征向量来作为神经网络的输入。当检测到故障发生时刻后,选取故障发生前后1个工频周期的 A、B、C 三相电流 IA、IB、IC以及零序电流分量IC作为特征提取的对象,并得到经过MODWT 变换后的各级小波细节系数,若直接用小波系数作为特征向量输入到神经网络中将会导致存储空间大和分类精度差等问题,通常特征向量的选取会使用相关的统计量。本文选择“总标准偏差的变化量”和“总均值的变化量”作为特征向量,其详细信息如下所示:
(1)总标准偏差的变化量为

式中,i=1,2,3,...,J;J 为 MODWT 的分解级数;N 为每一级采样点的数量;Dij为细节系数;μD,i为每一级细节系数的平均值;σDA为故障后一周期的总标准偏差;σDB为故障前一周期的总标准偏差。
(2)总均值的变化量为
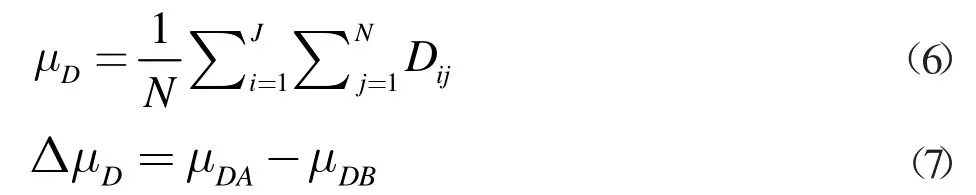
式中,i=1,2,3,...,J;J 为 MODWT 的分解级数;N 为每一级采样点的数量;Dij为细节系数;μDA为故障后一周期的总平均值;μDB为故障前一周期的总平均值。
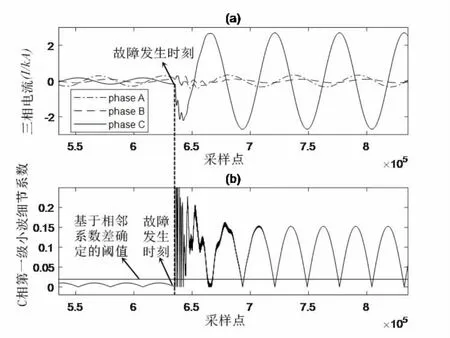
图2 使用基于相邻系数差的阈值法进行故障发生时刻检测案例
2.4 神经网络训练
LSTM 网络对于分析时序数据具有一定的优势,可以记忆长时间的数据,在预测时间序列和故障诊断等方面有应用。
文中LSTM 网络的神经元个数和其他参数的设置对网络的训练非常关键,将直接决定最终的分类效果,一般可以通过经验公式和不断试验来设置。文中具体的参数设置如表1 所示。
3 结果与分析
表2 为文中所提故障诊断方案的结果,分别统计了故障检测的识别率和故障分类的准确率。通过表2 可以看出:文中所提故障检测算法的总体故障检测率达到了99.33%,不同输电线路的检测准确率也可以达到98.99%以上,表明该检测算法是基本可行的。至于故障分类的性能则稍差一些,尽管如此,该方法仍可以提供令人满意的96.67%的整体分类精度,不同输电线路的故障分类准确率也可以达到95.45%以上。
表3 为不同故障分类算法的结果对比,将文中所提的故障分类算法和其他两种智能算法进行了对比。注意:其中效果最好的方案以粗体显示,这些比较方案的数据均由本文的测试系统提供,并且也使用文中提出的检测算法来检测故障。通过表3 的对比可以发现,在所有这些比较方案中,文中所提出的分类算法以最高的分类准确率优于其他智能方案,这也表明了该故障分类的算法也是基本可行的。
尽管所提出的故障诊断方案可以获得一个不错的故障检测和故障分类的结果,但对于故障检测来说,仍存在个别误检的情况,对于故障分类来说,仍存在个别错误判断的情况。主要原因是:在故障检测时,随着过渡电阻的增加,故障相的波形特性将无明显变化,因而其MODWT 变换后的一级小波细节系数的突变也会减小,而文中阈值的选取会一定地依赖于该突变,所以会导致个别误检。同时,也会导致故障分类区分的难度增加。
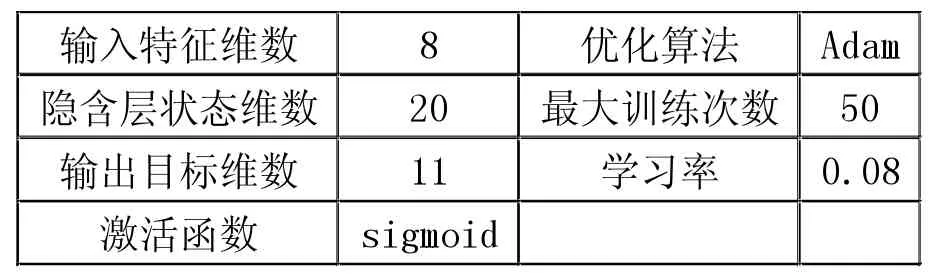
表1 LSTM 网络的参数设置

表2 故障诊断结果

表3 故障分类结果对比
4 结论
文中通过研究含分布式电源配电网的输电线路短路故障,首先采用了基于相邻系数差的阈值法实现了故障检测,接着将MODWT 变换和LSTM 神经网络结合实现了故障分类,诊断结果以及和其他智能方法的比较表明了该方案的有效性。尽管如此,该诊断算法在高过渡电阻情况下的准确率仍有待提高。
