基于BP 神经网络降低汽油精制过程中的辛烷值损失
2021-01-25刘都鑫孙啸宇
陈 曦,刘都鑫,孙啸宇
(北方工业大学 信息学院,北京 100144)
1 概述
目前,计算机模拟燃料配混是一个重要的研究方向,因为它大大减少了通过实验定义辛烷值的成本。过去的大量研究试图用数学方法将辛烷值描述为汽油成分。
所有这些方法都有优点和缺点。最大的兴趣是基于数学模型的开发复合过程的物理化学性质,因为模型考虑了特性的非可加性汽油。
许多模型基于回归分析,其形式为汽油不同性质的辛烷值函数,用于例如,蒸气压,密度和分数组成。这些方法有两个缺点。首先,模型有很多系数,需要重新计算原料含量变化。其次,这些模型没有考虑到原材料的变化文献综述表明,在过去的十年中,许多研究致力于优化复合工艺。然而,大多数计算混合辛烷值的方法都是建立在依赖任何物理和化学性质的基础上,而没有考虑混合过程的性质。
本文通过数学建模的方法,建立了一种辛烷值失损预测模型。首先通过PCA 降维的方法从在汽油生产过程中对辛烷值有影响的300 多个操作变量中筛选出20 个主要的操作变量,作为下一步建立预测模型的主要依据。随后利用BP 神经网络建立预测辛烷值损失的模型,最后利用最小二乘法来拟合汽油辛烷值和硫含量的分析,分析的结果可以画出汽油的辛烷值和硫含量的变化视图。
本文主要研究了辛烷值损失预测模型的建模与价值评估,需要解决优化操作中各个参数模型的优化、主要操作变量优化调整过程中对汽油中辛烷值硫含量的变化预测等问题。从而改善该模型的整体价值。
2 数据预处理
由于工厂得到的原始数据存在一定数据缺失和数据失真的情况,所以需要对数据中的坏值或者短缺值进行排除,对失真的数据进行修正。在选择方法数据处理方法上确定了多因素加权[1]的方法,并调整了表格中的参数,尽量保留有效参数,增加最终结果的泛化能力和鲁棒性。
数据处理方法步骤的确定:(1)对于残缺数据较多的点,进行整列的数据剔除。(2)删除325 个样本中数据全部为空值的位点。(3)对于空缺较少的位点我们采用通过周围点位取平均填补的方式。(4)总结出原始数据变量的操作范围,然后采用最大最小的限幅方法剔除一部分不在此范围的样本。(5)根据拉依达准则(3σ 准则)去除异常值。
3σ 准则:首先设对被测量变量进行等精度测量,得到x1,x2,……,xn,算出其算术平均值 x 及剩余误差 vi=xi-x(i=1,2,...,n),并按贝塞尔公式[2]算出标准误差 σ,若某个测量值xb的剩余误差vb(1<=b<=n),满足|vb|=|xb-x|>3σ,则认为xb是含有粗大误差值的坏值,应予剔除。
在这里主要通过3σ 准则,去除大量粗大误差值。取平均后求方差的步骤相比插值对算力开销有了很大的节省,整体效果比较稳定,如图1 所示。
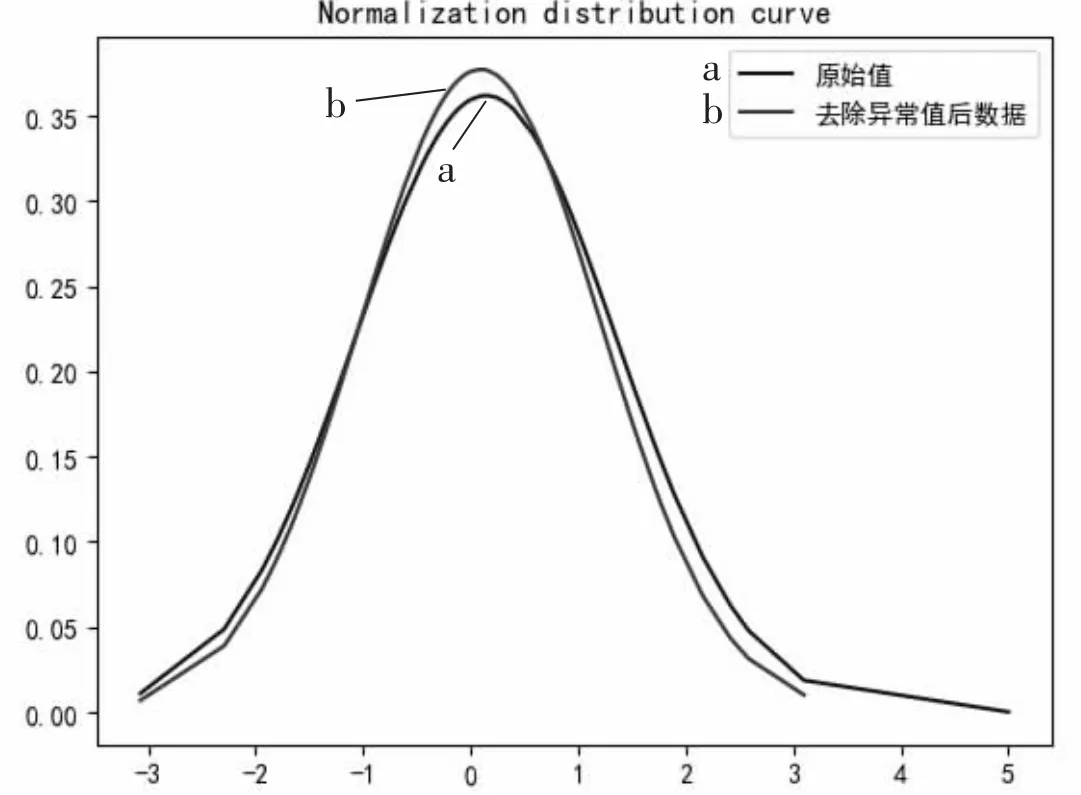
图1 去除异常值和原始值对比图
以下为在程序结果中截出的坏点和残缺点(图2,图3)。
3 数据降维
3.1 数据归一化
首先对样本数据进行处理,操作包括删除时间标号和样本编号等对降维无关的信息并把生产之后的辛烷值放到第一列作为其他操作变量是否进行降维的重要参考因素。
为使数据方便后续降维处理首先对数据进行标准化和归一化,标准化和归一化如图4 所示。
3.2 数据降维的目的
经过标准化和归一化的操作之后我们能准确的看出产品性质中的辛烷值的数值和原料性质中的辛烷值数值,为了二者准确表示出来,需要进行数据降维,325 个样本数据中用PCA 算法进行降维运算。降维的好处:(1)减少数据存储所需的空间,节约成本。(2)减少数据处理与建模的时间,提高效率。(3)提高该算法的性能因为会有一些算法在这300 维的数据上表现不佳。(4)有助于数据可视化能更直观地看出降维的结果。
3.3 数据降维方法的确定
在众多降维的算法中,PCA 算法具有耗时短而且速度快的特点,因此选用PCA 算法来进行降维[3],后文会详细说明建模主要变量的筛选过程及其合理性并将原料的辛烷值作为建模变量之一。
主成分分析(PCA):主成分分析通过累计的解释方差之和来判断主成分对所有特征的解释程度[4]。其两个性质为最大可分性和最近重构性也就是说使样本点尽可能分开保证样本点的方差最大化。
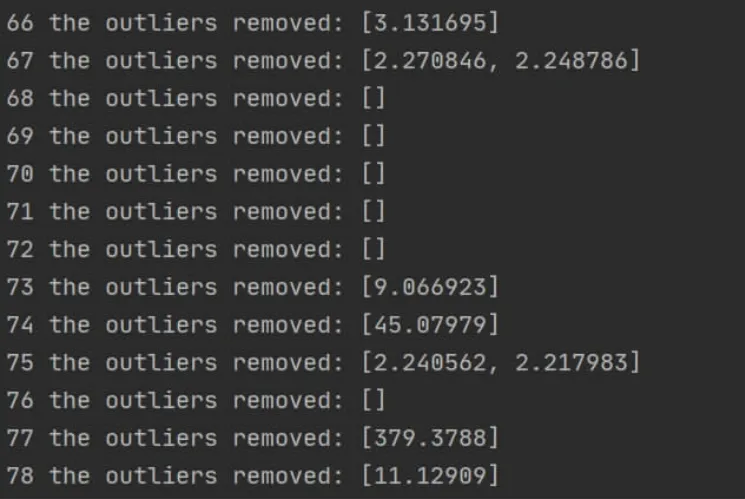
图2 误差值显示
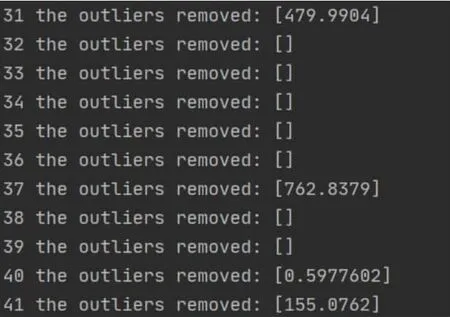
图3 误差值显示
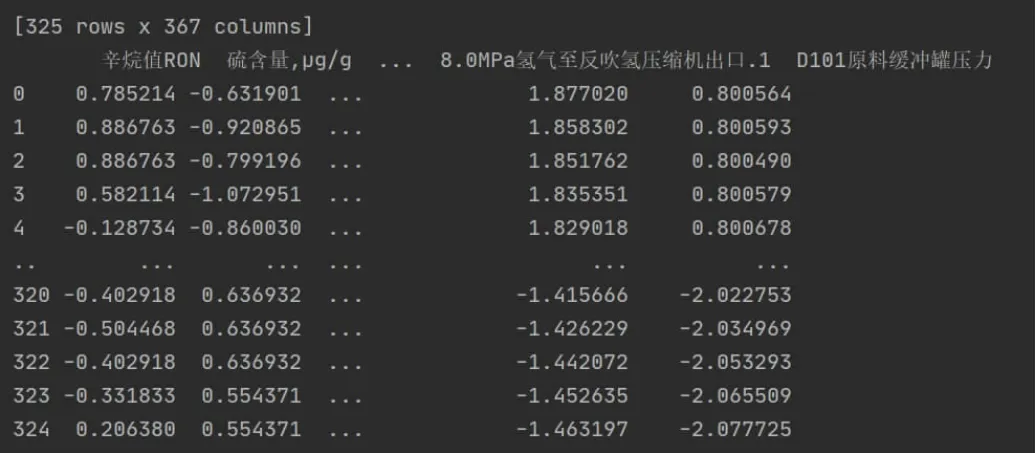
图4 标准化和归一化结果图
体操作步骤首先导出附录里操作变量指标所在的列接着对数据进行填补缺失值,补充完成后进行标准化根据问题二的要求选取主成分30 个最后观察主成分对特征解释的程度并绘制曲线。PCA 分量和累积解释方差如图5 所示。
图5 中柱状图一共30 个柱子,代表提取的30 个主成分,其高度代表每个主成分对方差的解释程度。
折线图代表30 个主成分对方差的累计解释程度。我们可以看到,30 个主成分对100 个特征方差的累计解释程度已经达到了80%,因此这30 个主成分携带了原始特征中的大部分信息,成功降维。
4 BP 神经网络预测模型的建立
首先,辛烷值与变量之间的关系并不明确,所以在这里应考虑线性和非线性两种关系,但在大多数情况下,在多尺度变量下,往往是非线性的,所以这里建立了非线性回归模型。回归分析的建立主要利用最小二乘法[5]计算自变量与因变量之间的映射关系,所以这里可以采用两种普遍方法,一是神经网络算法,二是BP 神经网络。
BP 神经网络按照有监督学习的方式进行训练,神经元把激活值从输入层经过各个隐藏层传给输出层,然后,从输出层经过各个隐藏层最终传给输入层,之后进行修正,因此把这样的反馈形式,称为“误差逆传播法”,随着不断地进行修正,整个网络响应的准确率也会不断提升。
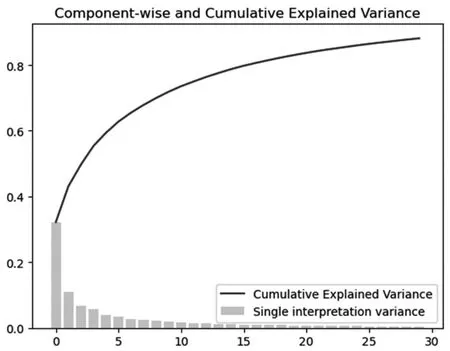
图5 PCA 分量和累积解释方差
4.1 BP 网络建模过程
本次建立的模型采用的是问题二中经过PCA 降维后所产生30 个主要操作变量的归一化[6]数据,此数据使用BP神经网络建立预测辛烷值损失的模型。在传统建立辛烷值损失模型的实验中存在原始数据过多,测试时间很长等问题。
整体包括3 层网络层,50 个隐藏层,1 个输入层和1 个输出层,并增加了激活函数f(neti),以防止发生过拟合的现象[7]。出现过拟合的情况时说明对于当前数据集的特征捕捉过于精准,导致模型的泛化能力较差,不能够在测试集中或者是此外的训练中产生利于推广的模型。
4.2 过拟合问题的解决
在实际操作过程中,产生了过拟合问题,训练出的分类模型如图6 所示。
由于的数据较少出现过了拟合的情况,针对这种情况,采取正则化的方式,在正则化中使用L2 正则化。
经过调整后,拟合程度有所下降,不再出现过度拟合的情况,图像的分类也不再过于集中,正常分类如图7 所示。
由图7 可以看到,通过增加L2 正则化我们的分类模型已经可以正常分类,经过优化后,损失函数LOSS 已经降到0.0964,并且泛化能力也相较之前的过拟合情况有了很大的提升,同时也大幅度的提高了模型的鲁棒性[8]。
5 模型可视化
模型的可视化,固定原料性质、待生吸附剂和再生吸附剂的性质数据保持不变,通过网络前期的震荡到平稳[9],记录此过程中的汽油辛烷值和硫含量的变化轨迹。该问题通过最小二乘法来拟合汽油辛烷值和硫含量的分析,分析的结果可以确定汽油的辛烷值和硫含量的变化视图。
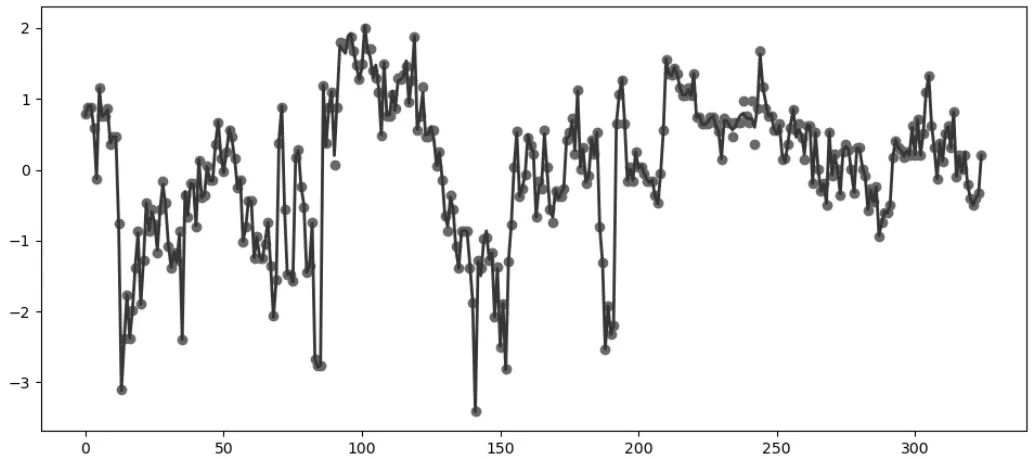
图6 过拟合情况
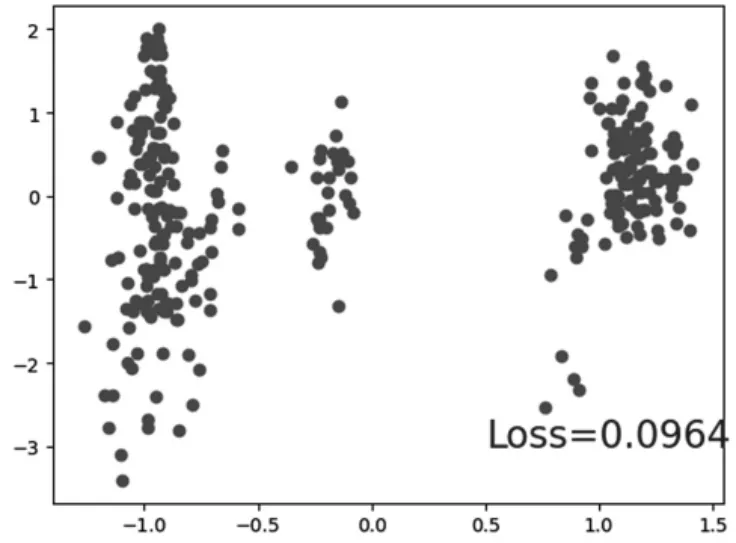
图7 正常分类
根据分析得出用最小二乘法计汽油辛烷值和硫含量模型中的参数N。
最小二乘法模型设P(β)为模型的输出代入公式求出结果:
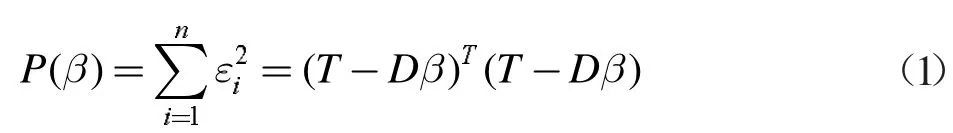
求出P(β)之后为了使β 尽可能的最小,因为β 的大小决定P(β)的好坏,所以接下来用P(β)得到β 的最小二乘估计,记作F,可由公式得出

算出F(2)之后的结果代回到E 的模型里来进行的估计值
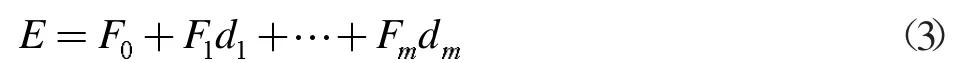
求出模型E(3)的估计值之后对汽油辛烷值和硫含量模型数据进行拟合,求出该模型的拟合为E′=D′B′,由最小二乘法算出拟合误差e=E-E′称为汽油辛烷值和硫含量模型该、残差,将随机误差Ψ 的估计可得出:
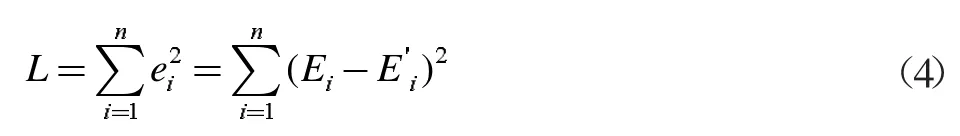
求出的L(4)即为汽油辛烷值和硫含量的最优调整系数。
6 结束语
本文对如何降低汽油精制过程中的辛烷值损失建立了数学模型并进行了分析,通过对数据的预处理[10]将数据进行归一化处理方便建立模型研究,接着使用PCA 主成分分析法对数据进行降维确保看出产品性质中的辛烷值的数值和原料性质中的辛烷值数值的变化,变得可视化,并用BP 神经网络来建立预测辛烷值损失的模型。该神经网络可以解决辛烷值损失模型的实验中存在原始数据过多,测试时间过长等问题。最后用最小二乘法大将模型可视化并优化油辛烷值和硫含量的调整系数。

图8 硫含量优化前后对比图
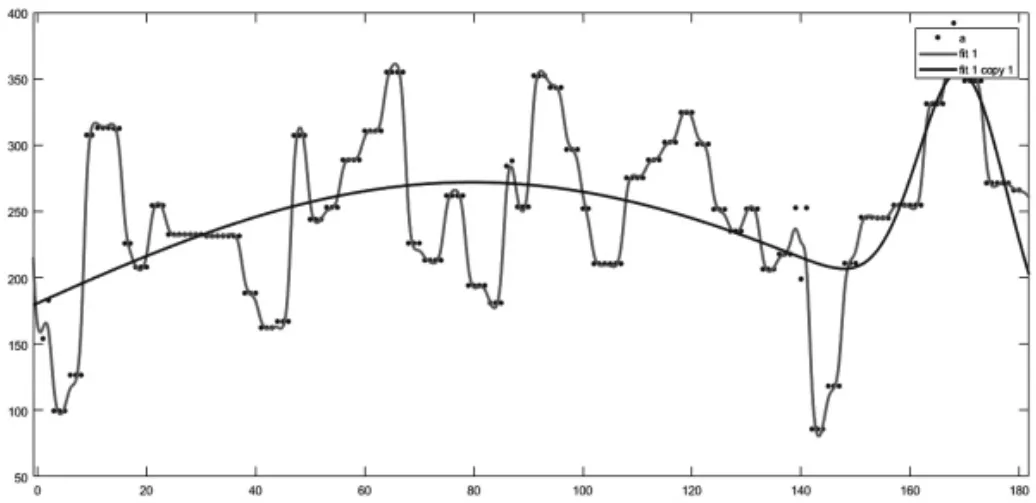
图9 汽油辛烷值优化前后对比图
