配电网馈线负荷自动预测及分布式电源接入方法研究
2021-01-23陈桂兰
陈桂兰
(通用技术集团工程设计有限公司,山东 济南 250031)
0 引 言
在用电量快速增长的背景下,人们对配电网负荷预测的精准度提出了更高的要求[1]。馈线线路是直接为用户送电的线路。馈线负荷预测结果的精准度会影响工作人员对发电机组的操作。结果过高会降低电力设备利用率,浪费闲置资源;结果过低会在用电高峰期造成电力系统过载甚至满载的危险,降低了电力系统的安全性[2]。配电网负荷自动预测精度的提高,有利于提高电力资源的利用率,减少能耗,指导新增电力机组的组装,具有十分重要的经济价值。本文基于传统配电网馈线负荷自动预测方法,研究配电网馈线负荷自动预测和分布式电源接入方法,对其进行优化,从而提高其预测精度。
1 分布式电源接入
一些分布式电源并网运行需要通过电力电子装置(逆变器或整流器)与系统连接,如太阳能光伏发电、储能系统、微型燃气轮机以及燃料电池等。其中,太阳能光伏、储能系统以及燃料电池发出的是直流电,需要通过DC/AC逆变器与电网相连。而对于微型燃气轮机发出的高频交流电,则需要通过AC/DC/AC或AC/AC变频后才能并网。所有需要逆变器并网和采用电压控制策略的分布式电源,大都可作为PV节点来处理。
2 构建配电网馈线负荷自动预测模型
2.1 设定黑盒框架
设定样本数Nd为整数,采样时间Ts为15 min,用x(k)表示从原点到时间kTs的样本变量,将预测提前时间λ的负荷作为问题,选择参数映射f(·;θ),在时间k+λ处对负荷y建模:
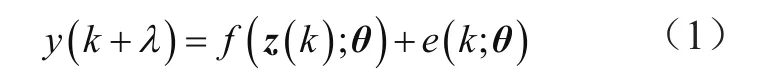
式中,z(k)表示回归向量,包含在k处的可用信息;k为自然数,表示离散时间指数,使参数矢量θ=θ*,以调整误差e(k;θ),使其相对于评估数据范数最小化。
预测提前时间λ的公式为:
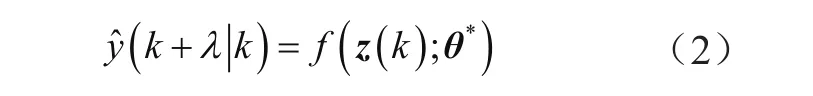
式中,y^为合取运算后的负荷。
2.2 改进SVM回归函数
用函数f(x)=[w·∅(x)]+b拟合线性回归。当xi∈Rn作为训练样本集(xi,yi)ni=1的输入值时,yi∈R即为相应输出值。依照统计理论,对目标函数进行极小化处理,得出:
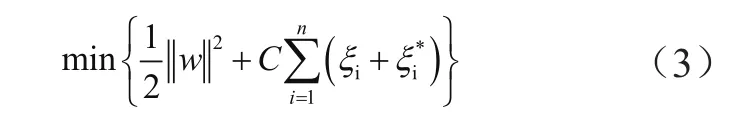
约束条件为:
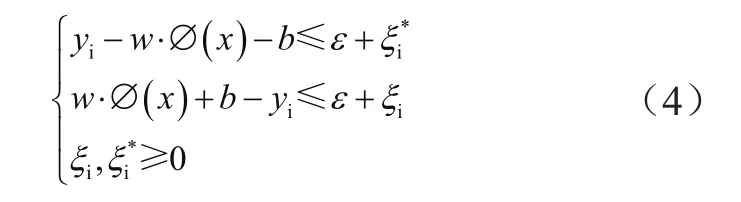
式中,ε为不敏感损失函数;C为惩罚因子;w为权值;ξi和为非负松弛变量;b为分辨系数。
于是,整理可得:
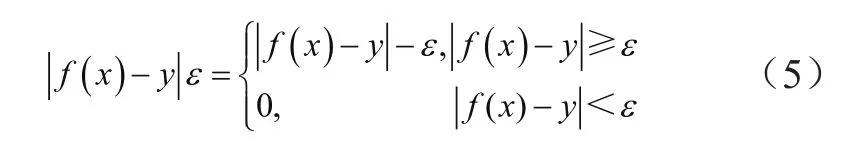
将其转化为对偶问题:
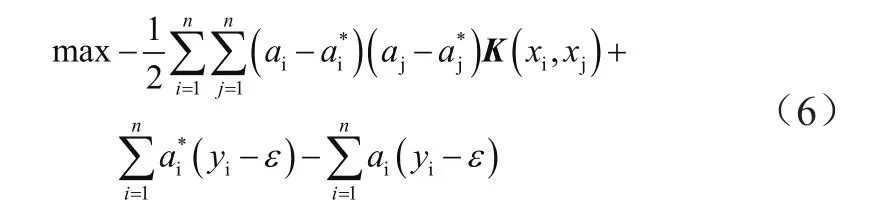
约束条件为:
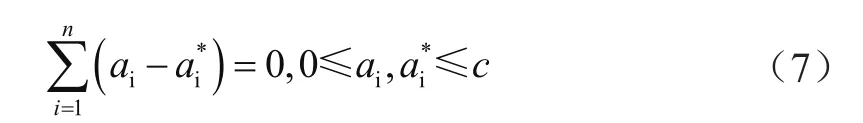
将RBF基函数选为核函数:
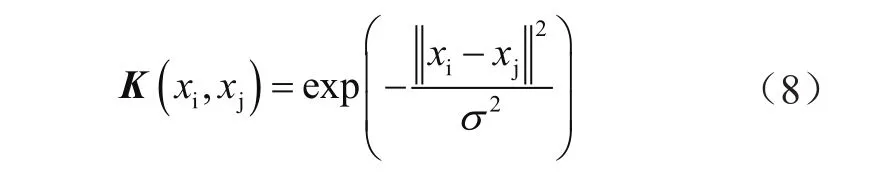
式中,K为评价因子矩阵;σ为标准差。
综上,得到SVM回归函数为:
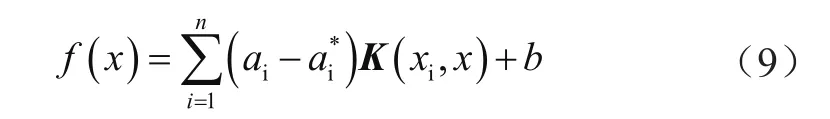
当ai-ai*≠0时,支持向量为对应的训练样本,此时b需满足以下条件:
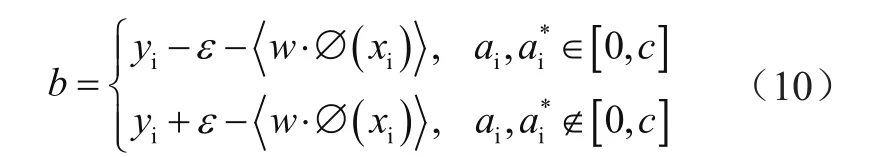
在n维空间中,某一位置的第i个粒子为参数样本。通过算法搜索粒子最优位置Pi,用Vid表示粒子i的移动速度,其中d=1,2,3,…,n,对比粒子位置进一步确定粒子群的最优位置Pgd。
迭代过程中,粒子i的移动速度为:
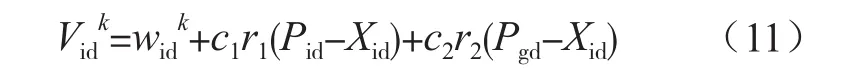
粒子i更新位置为:

惯性权重因子为:
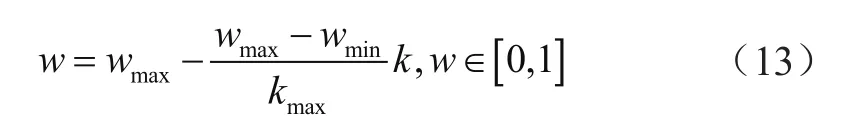
式中,X为粒子位置;k为当前迭代次数;c1、c2为加速因子;r1、r为[0,1]之间的随机数。
利用粒子群优化算法对SVM回归函数中的参数进行最优选择,使函数中的重要参数得到优化,完成在黑盒框架下的建模。
3 配电网馈线负荷自动预测
3.1 选取预测结果评价指标
在传统的预测方法中,通常凭借单一的指标评价某种预测方法。为了提高评价的准确性,本次研究中选取均方根误差和平均绝对误差两个指标。
均方根误差(Root Mean Square Error,RMSE)为:
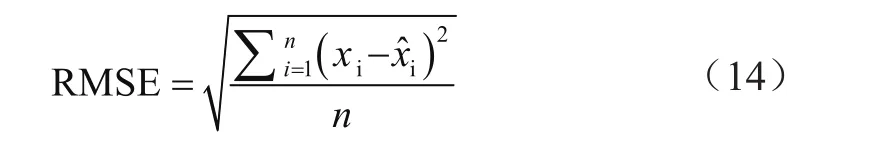
平均绝对误差(Mean Absolute Error,MAE)为:
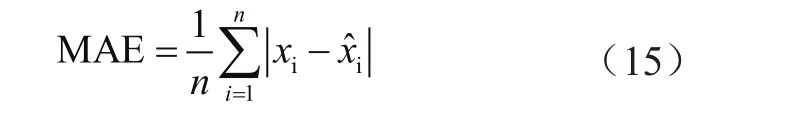
式中,xi为负荷真实值;x^i为负荷预测值;n为预测点数。
用误差类的指标来表示负荷的预测结果与真实值之间的差异情况[3]。
3.2 输入预测变量
在改进后的回归函数基础上,选取可以使AD响应负荷变化的输入变量z(k),结构如下:
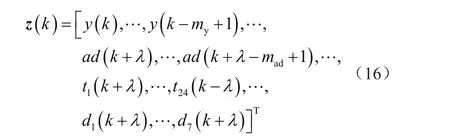
式中,a为日类型差异;d为天数;my与mad为固定的整数。通过二进制变量ti(k)和dj(k)在一周中选取某一天,并在一天中选取某一时刻。当时间指数k落入一周中的第j天(j=1,…,7)第i小时(i=1,…,24)时,其对应的变量dj(k)=1、ti(k)=1。
由回归向量式(16)可以确定式(4)中的参数映射f(·;θ),有:
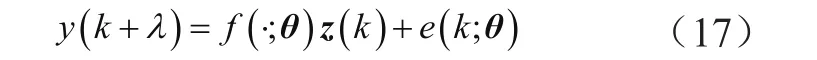
式中,θ∈Rmy+mad+31为参数向量,能够按照经典最小二乘法估算。
考虑到配电网馈线负荷受外界因素影响严重,为保证输入变量具有参考性,将天气条件等纳入变量输入中,采用时变方程:
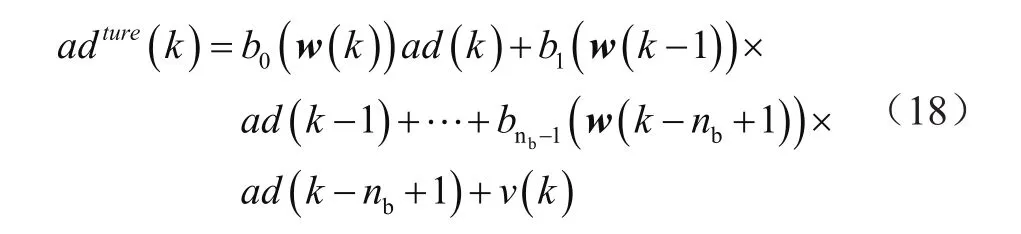
式中,v为关联度;w(k)为包含外部因素的矢量;nb为最大负荷数据。将bi(w)(i=1,…,nb-1)线性参数化,以方便将式(16)与负荷自动预测模型合并[4],有:
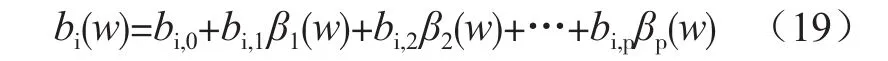
式中,βj(w)是带有w的函数,其中j=1,…,p。此时,式(17)中的回归向量z(k)还应包含:
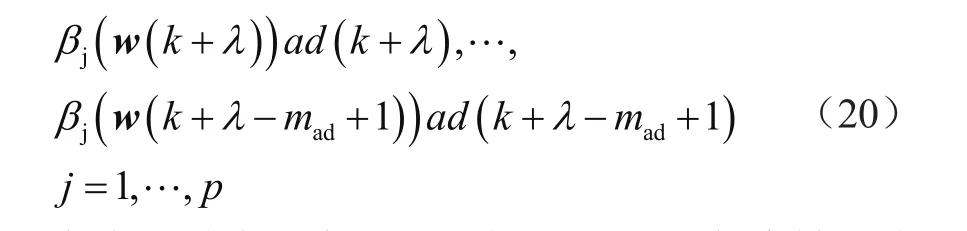
在应用时应注意,外部信号w(w)可能会被相应的预测信号代替。结合天气情况或者电价预测等,在构建的模型中输入预测变量,从而完成配电网馈线负荷自动预测[5]。
4 模拟预测
为了验证模型的有效性,选取某地某年配电网小时负荷及温度特征历史数据作为真值,分别模拟4个季度的配电网馈线负荷自动预测数据。其中,将提出的方法标记为方法1,将杨楠等与高嘉豪等提出的传统方法分别标记为方法2与方法3。利用3种方法分别对配电网馈线负荷与净负荷进行模拟预测[2,3]。
4.1 配电网馈线负荷自动预测模拟结果
分别对3种方法进行模拟预测,得到的负荷值结果如图1所示。由图1可知,3种方法模拟预测的负荷值结果大致走势相同,方法1得到的结果与真实值更接近。
将3种方法模拟预测结果与真值进行对比,计算均方根误差(RMSE)和平均绝对误差(MAE)得到的数据分别如表1和表2所示。
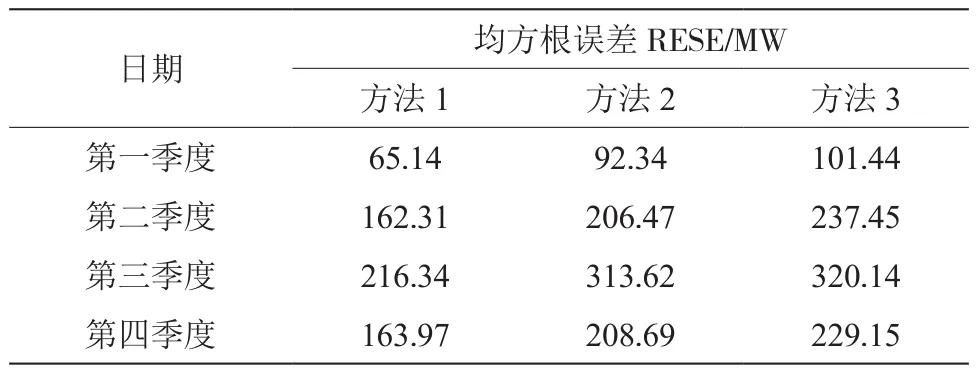
表1 3种方法负荷预测值均方根误差比较
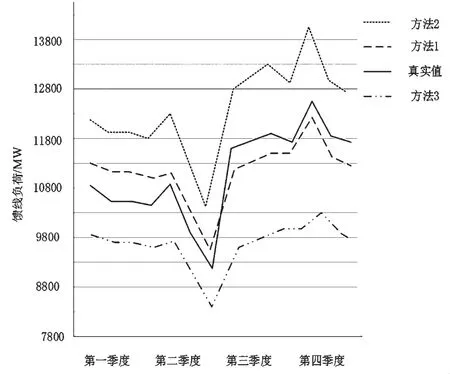
图1 某年配电网馈线负荷自动预测模拟结果对比图
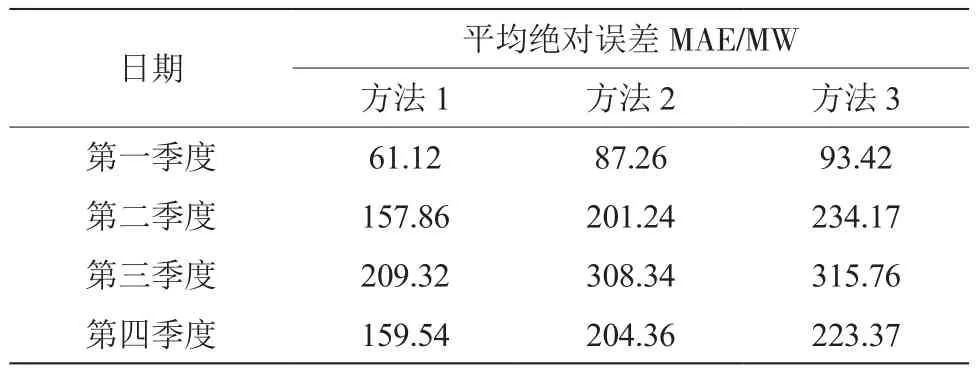
表2 3种方法负荷预测值平均绝对误差比较
由表1可知:在第一季度的数据中,方法1的均方根误差为65.14 MW,相比于方法2和方法3分别低了27.2 MW、36.3 MW;在第二季度的数据中,方法1的均方根误差为162.31 MW,相比于方法2和方法3分别低了44.16 MW和75.14 MW;在第三季度的数据中,方法1的均方根误差为216.34 MW,相比于方法2和方法3分别低了97.28 MW和103.8 MW;在第四季度的数据中,方法1的平均绝对误差为163.97 MW,相比于方法2和方法3分别低了44.72 MW和65.18 MW。
由表2可知:在第一季度的数据中,方法1的平均绝对误差为61.12 MW,相比于方法2和方法3分别低了26.14 MW和32.3 MW;在第二季度的数据中,方法1的平均绝对误差为157.86 MW,相比于方法2和方法3分别低了43.38 MW和76.31 MW;在第三季度的数据中,方法1的平均绝对误差为209.32 MW,相比于方法2和方法3分别低了99.02 MW和106.44 MW;在第四季度的数据中,方法1的平均绝对误差为159.54 MW,相比于方法2和方法3分别低了44.82 MW和63.83 MW。
4.2 配电网馈线净负荷自动预测模拟结果
分别对3种方法进行模拟预测,得到的净负荷值结果如图2所示。
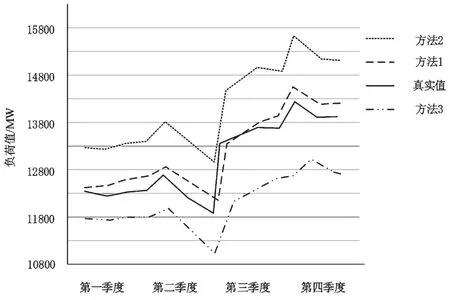
图2 配电网馈线净负荷自动预测模拟结果对比图
由图2可知,3种方法模拟预测的净负荷值结果大致走势相同,方法1得到的结果与真实值更接近。对比得到的结果与真实值,计算均方根误差(RMSE)和平均绝对误差(MAE)得到的数据分别如表3和表4所示。
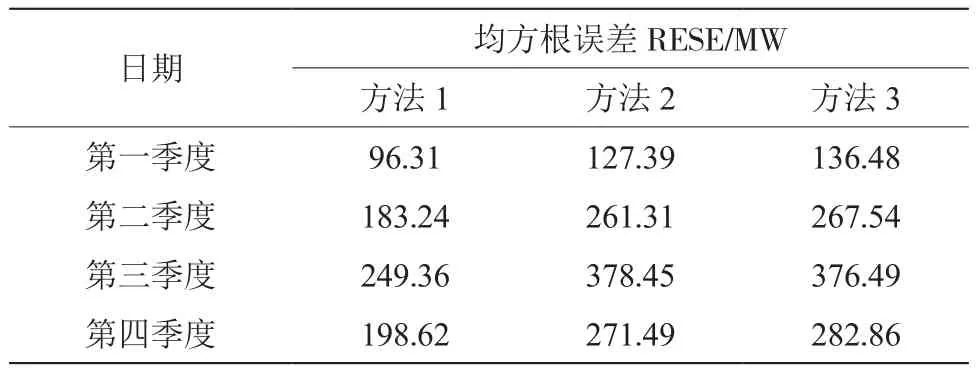
表3 3种方法净负荷预测值均方根误差比较
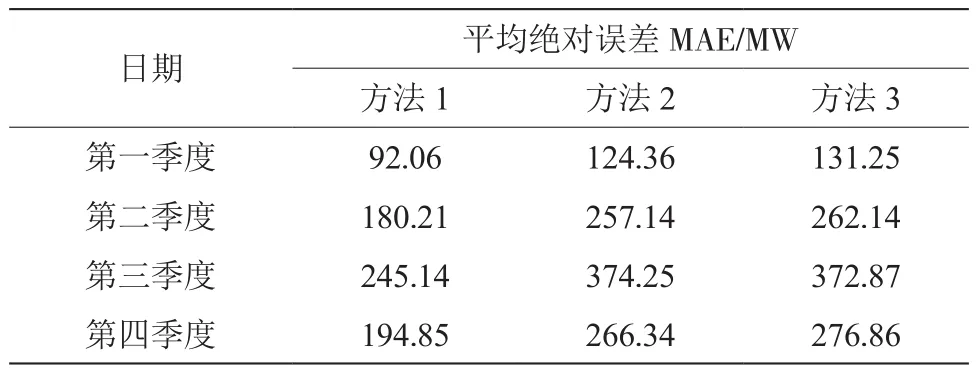
表4 3种方法净负荷预测值平均绝对误差比较
由表3可知:第一季度的数据中,方法1的均方根误差为96.31 MW,相比于方法2和方法3分别低了31.08 MW和40.17 MW;第二季度的数据中,方法1的均方根误差为183.24 MW,相比于方法2和方法3分别低了78.07 MW和84.3 MW;第三季度的数据中,方法1的均方根误差为249.36 MW,相比于方法2和方法3分别低了129.09 MW和127.13 MW;第四季度的数据中,方法1的平均绝对误差为198.62 MW,相比于方法2和方法3分别低了72.87 MW和84.24 MW。
由表4可知:第一季度的数据中,方法1的平均绝对误差为92.06 MW,相比于方法2和方法3分别低了32.3 MW和39.19 MW;第二季度的数据中,方法1的平均绝对误差为180.21 MW,相比于方法2和方法3分别低了76.93 MW和81.93 MW;第三季度的数据中,方法1的平均绝对误差为245.14 MW,相比于方法2和方法3分别低了129.11 MW和127.73 MW;第四季度的数据中,方法1的平均绝对误差为194.85 MW,相比于方法2和方法3分别低了71.49 MW和82.01 MW。
由表5可知:第一季度的数据中,方法1的平均绝对误差百分比(Mean Absolute Percentage Error,MAPE)为4.75%,相比于方法2和方法3分别低了1.88%和2.17%;第二季度的数据中,方法1的平均绝对误差百分比为4.11%,相比于方法2和方法3分别低了1.8%和1.87%;第三季度的数据中,方法1的平均绝对误差百分比为3.95%,相比于方法2和方法3分别低了1.79%和2.09%;第四季度的数据中,方法1的平均绝对误差百分比为4.32%,相比于方法2和方法3分别低了1.51%和1.85%。
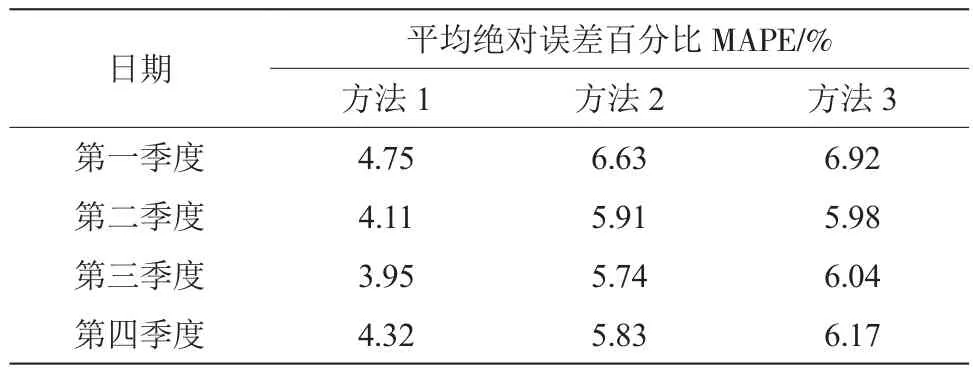
表5 3种方法净负荷预测值平均绝对误差百分比比较
5 结 论
本文通过优化配电网馈线负荷自动预测及分布式电源接入方法,提高了配电网馈线负荷自动预测的精准度,增强了配电网运行的稳定性,有效降低了发电成本,为城市新发电机组的安装提供了参考。日后,研究人员应更深入地研究配电网馈线负荷自动预测方法,以促进配电网自动化的发展。
