“三个理解”视角下弧度制概念引入的比较
2021-01-22江苏省太湖高级中学214125
何 英 (江苏省太湖高级中学 214125)
《普通高中数学课程标准(2017年版)》指出:高中数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新意识,提升数学学科素养. 《国家中长期教育改革和发展规划纲要(2010—2020年)》提出:关心每个学生,促进每个学生主动地、生动活泼地发展,尊重教育规律和学生身心发展的规律,为每个学生提供适合的教育. 这些表述明确而清晰地告诉我们本次课程改革应以生为本,通过对数学核心素养的培养,完成立德树人的根本任务. 怎样的数学教育才是“面向全体学生,促进人人成才”的教育?教师如何在数学概念教学中有效达成这些目标,使得“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”?章建跃先生在评价一节好课时,提出了“三个理解”的标准,即理解数学、理解学生和理解教学,笔者深以为然,认为教师只有在“三个理解”上狠下功夫,才能在数学课堂上达成这些目标. 本文将从“三个理解”的角度比较两节省级优质课在建构弧度制概念这个环节的不同处理.
1 原案展示
案例一
· 情境引入
问题1:生活中有很多几何量,比如摩天轮上某个点P的位置与哪些量有关?
问题2:角度和长度的单位分别是什么?多少进制?
问题3:这两个几何量进制不一致,会给研究带来不便,怎么办?能否像长度一样用十进制的实数度量角?
· 建构概念
问题4:生活中对于同一个量,度量结果可以用不同的单位表示吗?请举例说明.
问题5:图1中哪些几何量能唯一确定角α?

图1
(学生先独立探究,再小组交流)
问题6:怎么证明?
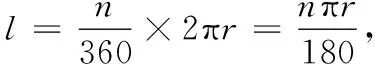
问题7:根据以下数学史,思考如何建立一种新的度量角的制度.
数学史:(1)不同时期“尺”的单位1的不同定义;(2)1度角的规定.
(学生先独立探究,再小组交流)
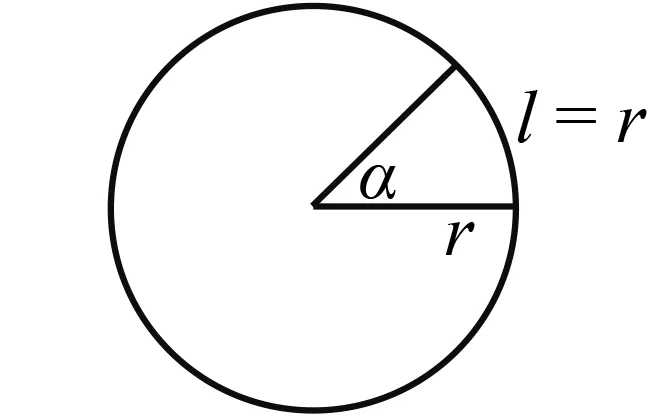
图2
师:非常好!大家定义了一种新的度量角的方式. 大数学家欧拉也跟大家一样的想法,1748年欧拉提出把半径作为弧长的度量单位,使一个圆周角等于2π弧度,也就是把长度等于半径长的弧所对的圆心角叫做1弧度,记为1 rad,用弧度作为单位来度量角的单位制称为弧度制.
案例二
· 情境引入
问题1:老师身高5.25英尺,体重110磅,大家听完这组数据知道教师身高体重的具体情况吗?
问题2:我们更熟悉什么单位?
·建构概念
问题3:角的度量单位是什么?1度的角是如何规定的?
问题4:能否用弧长度量角?带着问题,我们从特殊到一般,来探索规律. (完成表1)

表1
问题5:能否用表1中第一列的弧长反映圆心角的大小?你能重新找一列数来反映这些角的大小吗?
问题6:给定圆心角,若给定半径,你能找到一个量来度量圆心角吗?若半径变化,你能找到一个量来度量圆心角吗?
实验操作:(几何画板演示)
问题7:能用长度度量角度吗?用什么量?
问题8:你能从数的角度给出理论推导吗?
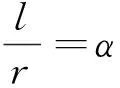
2 听课感悟
两位教师在概念建构环节的设计不同,课堂呈现的教学效果也不同. 笔者从“三个理解”角度对 这两节课做了一些比较,不当之处,请同行指正.
(1)理解数学,厘清概念的前世今生
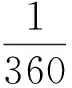

(2)理解学生,以学定教促人人成才
理解学生就是要理解学生的学习心理,包括学生的知识储备、学习习惯、学习热情、创新能力、团队精神、意志毅力等诸多要素. 这两堂课的授课对象来自一所老牌四星级高中,生源好,学生数学素养一流. 面对这样的学生教师如何定位自己的角色,如何通过自己的教学智慧和数学素养来展现数学的魅力、激发学生学习数学的原动力、保持课堂的活力,这是非常重要的课题.

(3)理解教学,取舍中运化教学之道


真正做好三个理解是不容易的,需要教师有深厚的数学素养和教育修养,也需要教师在备课时做大量的资料查阅、了解学情等工作,工作繁琐且在短期内可能看不到明显成效. 但是为了能在数学课堂中真正落实数学核心素养的培养、提高新时代学生的基本素质,这些又都是值得的.
