核心素养视角下数学原理的教学探讨*
2021-01-22崔静静廖远鸿西昌学院理学院615013
崔静静 廖远鸿 (西昌学院理学院 615013)
赵思林 (内江师范学院数学与信息科学学院 641110)
数学中的原理主要包括公式、法则、定理、性质[1]. 数学原理的探究、发现(猜想)、证明、应用、拓展(变式)是学生获得数学核心素养的重要渠道. 从培养学生核心素养的角度来看,数学的公式、法则、定理、性质的教学,有不同的教学过程与规律.
1 数学原理的教学理论
数学原理学习的本质包含两方面的内容:一是作为客观的数学原理,即对原理的客观陈述,具体表现为用言语符号等描述概念间的关系;二是作为主观的数学原理,它体现了人的心理操作反应系统. 数学原理的教学不仅需要学生习得描述数学原理的言语符号信息,更需要习得学习这些数学原理的心理意义,构成有意义学习.
数学原理的学习可划分为4种依次递增的水平:言语连锁水平、正向产生式水平、逆向产生式水平、变形产生式水平. 其中变形产生式水平是最高的学习水平,它是创新思维的基础,表现为能综合运用数学原理解决问题,在数学教学中通常以推广和引申的形式呈现. 因此,习得数学原理绝不是孤立地掌握某个数学原理,而是要在各数学原理之间建立联系,形成完备的体系.
2 核心素养视角下数学原理的教学探讨
核心素养体现了教育的终极目标就是要落实到人身上,个体在经受学科教育后,习得的气质、思维方式等将不同于未经这种学科教育的个体.[2]数学核心素养有着其独特的使命,它不仅承担着培养学生数学抽象、逻辑推理等六方面的素养,还肩负着培养“四能”的职责. 学生获得“四能”,形成独特的学科思维,拥有发现数学的头脑,实现“再创造”,这才是学生获得核心素养的最高级表现. 课堂是培养学生数学核心素养的主阵地,数学概念、原理的教学是培养学生核心素养的良好载体. 一般地,数学原理的教学过程和培养的核心素养的关系如图1所示. 下面将从培养学生核心素养的视角,谈谈数学公式、法则、定理、性质的教学.
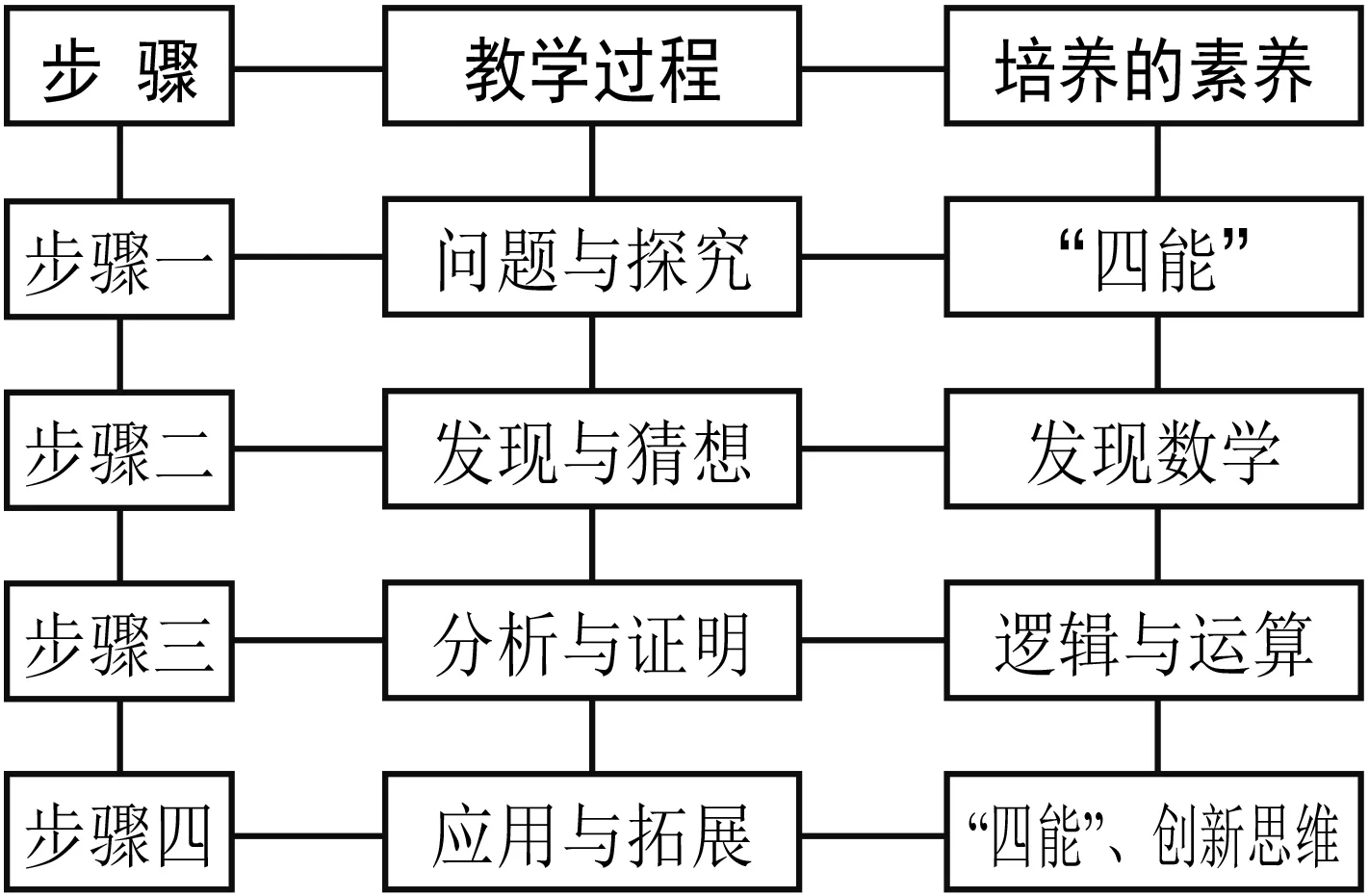
图1
2.1 数学公式的教学
关于公式的教学,给出以下四条教学策略. 首先,重点把握公式的推导过程,让它成为发展学生数学运算和逻辑推理核心素养的重要载体. 其次,应注重探究它在数学知识体系中的来龙去脉、产生过程,让学生加深对数学本质的理解. 再次,引导学生对公式的结构、内涵进行分析,以此加深对公式的深度理解,体会其中蕴含的数学抽象之美. 最后,加强新旧公式的关联比较,促进对公式的逻辑性理解.
案例1“三角函数诱导公式”的教学.
不少师范生经常这样导入新课:如何求sin 420°的值. 从揭示数学知识的内在联系来看,显然这个孤立问题的启发性是不够的. 首先,学生借助计算器等现代技术手段就能快速获得答案,并没有体现诱导公式的作用. 其次,这个问题过于僵化和实用,不能给学生提供广阔的思维空间,从而降低了诱导公式这部分内容的教育价值. 最后,这个问题过于独立,很难与其他知识进行串联,从整体上认识这部分知识.
那么,要培养学生的核心素养,不妨按照图1的技术路线进行教学. 通过上节课的学习,我们知道三角函数可用于刻画周期现象,那它是通过何种方式来刻画周期现象的?用这种问题与探究的方式导入新课,给学生提供广阔的思维空间,让他们分析与解决问题的能力得到发展. 借助单位圆,引导学生进行发现与猜想,按照“点的周期性运动→角的周期性运动→三角函数的周期性运动”的思路进行探究,建立用三角函数刻画周期现象的数学模型,得到诱导公式sin(2kπ+α)=sinα(k∈Z). 对于其他几组诱导公式,同样可以用这样的探究思路,将终边对称的图形转化为三角函数间的代数关系[3]. 最后将公式总结为“奇变偶不变,符号看象限”.
案例2分类加法和分步乘法公式的应用.
计数原理包括分类计数原理和分步计数原理,二者分别对应着加法原理和乘法原理. 计数原理的应用常见于组数问题、映射问题、分配问题、与几何有关的计数问题、涂(染)色问题、约数问题.
问题与探究1集合A={1,2,3,4},B={5,6,7},从A到B的映射有多少个?
推广1 集合A={1,2,3,4},B={a,b,c,d},从A到B的映射有多少个?其中一一映射有多少?
引申1 现有4个人去住3个房间. 问:有多少种住法?每个房间都不空着又有多少种住法?
引申2 设集合A={-1,0,1},B={2,3,4,5,6},从A到B的映射f:A→B,使对任意的x∈A,都有x+f(x)+xf(x)是奇数,求这样映射的个数.
问题与探究1是分步计数原理的简单应用,对该问题进行推广与引申,实现了从简单向复杂的逐步转化. 与映射、一一映射联系,设置逐级抽象的问题,让学生的思维受到启发,加强了对映射、计数原理关系间的理解,对知识进行了横向和纵向的延伸,培养了他们的抽象思维、逻辑素养.
案例3与几何有关的计数问题.
问题与探究2如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有多少对?
思路1 由分类计数原理,如图2所示,与AB成异面直线的有4对,与BC成异面直线的有4对……这样的情况共六类. 按照分类加法原理,构成异面直线共有4+4+4+4+4+4=24对.

图2
思路2 由分步计数原理,构成异面直线共有6×4=24对.
通过对该几何问题的探究,能让学生明白加法原理和乘法原理可用于解决同一问题,对两者的关系有了进一步的理解. 通过分析用哪一种计数原理以及如何实现分类或分步,培养了学生分析与解决问题的能力,发展了学生的“四能”.
公式的产生绝不是“孤零零”存在的,也不是靠死记硬背保留在大脑中的. 讲清公式的来龙去脉,不仅能促进学生对公式的深刻理解和记忆,它的推广、引申、应用更是培养学生直观想象、“四能”、创造性思维的良好途径.
2.2 数学法则的教学
运算法则指为达到一个问题的解决方案而定义的规则或过程,一般的运算法则指加减乘除四则运算. 更复杂的运算法则也是对简单的加减乘除四则运算法则的继承、演变与发展. 法则的教学能够较好地培养学生的数学运算、逻辑推理、数学抽象核心素养[4]. 高中数学最早提到“法则”是在函数定义中,接着是指数幂的运算、对数、导数等.
案例4对数的运算法则.
问题与探究3如果a>0,且a≠1,M>0,N>0,证明:loga(MN)=logaM+logaN.
推广1 当M=N时,上式满足什么关系?由此可猜想logaMn=?logambn=?
显然,对数的换底公式由对数定义和推广1推导得来. 下面以推广2为抓手,进一步推广. 以问题的形式呈现,引发学生思考,锻炼了学生分析与解决问题的能力,培养了学生的“四能”和数学运算、逻辑推理核心素养.
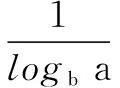
推广4 猜想loga1a2·loga2a3·loga3a4·… ·logan-1an值为多少,并证明之.
推广5 猜想loga1a2·loga2a3·…·logan-1an·logana1值为多少,并证明之.
先引导学生对以上问题进行合理猜想,再进行分析与证明,由此使得学生的运算素养、逻辑推理能力得到发展,并潜移默化地促进他们猜想、质疑精神的生长.
在数学概念和法则教学中,当遇到一个新的概念和法则时,总希望它与已有的概念和法则建立联系. 如学习减法时与加法联系,学习除法时与乘法联系,学习对数时与指数联系等. 若已有的法则没有学扎实,基础没有打牢,势必会影响与之联系的后续学习. 因此数学法则的教学要多关注与之有关的法则,在学习新法则之前能够熟练地对已有的法则进行“正用、逆用、变形使用”,使新旧法则相容,达到知识的融会贯通.
2.3 数学定理的教学
数学定理的教学是高中数学教学的重点和难点. 定理的教学通常是培养学生的逻辑推理、直观想象、数学抽象等核心素养的良好载体. 定理的教学方式可分为问题解决型、结果呈现型两种教学交互模式[5]. 问题解决型的教学交互模式建立在发现探究学习、情境认知理论的基础上. 下例是正弦定理与余弦定理的综合应用,引导学生观察、探究、发现三角形边角设置的巧妙性,找准方法是正确列出式子的前提.
案例5正弦定理与余弦定理的综合应用.

该问题是对角平分线的性质、正弦定理、余弦定理以及二倍角公式的综合考查,需要学生有较强的综合能力,适宜设计在余弦定理一节上完后,作为能力提升题型出现. 教师应给予学生足够的时间进行思考,学生可能因无法将这些知识综合运用而出现不适感,这就需要教师引导学生对其进行探究与发现,发现知识间的关联性,而非单一地对余弦定理题型进行演练. 这样的题型必定是培养学生数学运算、逻辑推理能力,发展学生学科思维,让学生具有数学智慧的良好载体.
2.4 数学性质的教学
逻辑推理是得到数学结论的重要方式,是进行数学学习活动的基本思维品质. 数学中大多数定理、性质的教学都离不开逻辑推理,如函数的单调性、奇偶性、周期性的教学.
案例6函数的单调性.
高中数学必修1在编排函数的单调性一节时. 首先呈现的是观察一次函数f(x)=x和二次函数f(x)=x2图象的变化趋势. 不少师范生在试讲时“照猫画虎”,没认识到函数单调性的内涵,不理解单调性的逻辑关系,就“依葫芦画瓢”先分析图象,看出图象的单调性后,再理所当然的证明单调性. 究竟是从图象上发现该函数是单调的,才去证明它是单调的?还是研究该函数有这样的单调性才导致图象的单调性?正确的逻辑关系显然是后者.[6]
案例7函数的奇偶性.
关于函数的奇偶性一节,教材首先让学生观察函数f(x)=x2和f(x)=2-|x|图象的共同特征,再回答它们函数值对应表是如何体现这些特征的. 同样也有不少教者模仿教材“依葫芦画瓢”,这样的教学是“肤浅”的——没有理解函数奇偶性内在的逻辑关系. 拿函数f(x)=x2来说,究竟是从其对称图象上发现f(x)与f(-x)的关系,还是因为有了f(x)=f(-x)的关系,才导致图象的对称. 明显后者是成立的. 基于以上分析,要培养学生正确的逻辑推理思维,不妨引导学生思考:
问题与探究5为什么函数f(x)=x2和f(x)=2-|x|的图象均关于y轴对称?
引导学生分析、发现这两个函数解析式的特点与函数值间的关系,再将函数值间的关系转化为点间的关系.[7]教材中诸如此类性质的推理还有很多,这里就不再赘述. 一般地,数学性质通常由概念推导而来,性质的教学应从构成性质的要素出发,厘清其中逻辑关系. 以此加深学生对概念的深刻理解,培养学生的逻辑推理能力.
3 结语
数学核心素养不是教师直接以口耳相传的方式教出来的,而是在一系列的数学探究性活动中通过问题的发现与提出、问题的分析与解决、结论的猜想与证明,潜移默化培育起来的. 学生能够领悟原理教学中所蕴含的数学思想方法,形成理解和分析问题的学科思维能力是数学核心素养形成的最高表现.[8]数学核心素养的获得紧紧地依靠着教师设计的探究活动. 数学核心素养的培养,最终是落实到学生个体,数学原理的教学就应以学生为本,教学的重中之重则应从简单机械的“教知识”转向“如何教才能促使学生更好地学”,在教师的引导下开展深度学习和自主学习. 数学的公式、法则、定理、性质的学习,是学生获得数学知识、领悟数学思想方法、积累数学活动经验、感受数学之美的重要载体,不仅对学生的升学考试有着决定性的作用,同时也润物细无声般地影响着学生的审美、智慧、眼光等.
