复杂场景下的改进核相关滤波跟踪算法

王 蓓，陈金广，王明明

1.西安工程大学 计算机科学学院，西安710048

2.柯桥区西纺纺织产业创新研究院，浙江 绍兴312030

视频目标跟踪是计算机视觉中重要的组成部分，在智慧城市、虚拟现实、公共安全监测、机器视觉等实际应用中起到关键作用。目标跟踪算法在近些年的发展中大致分为三个研究方向[1]：深度学习方向[2-6]、相关滤波方向[7-12]和传统的跟踪算法方向[13-15]，而在实际跟踪环境中，传统方法在面对尺度变换、复杂背景、遮挡等跟踪问题时难以满足准确性、快速性和鲁棒性。而基于深度学习的目标跟踪算法面对上述问题时，跟踪精度虽然能够保障，但跟踪实时性较差。近十年发展起来的相关滤波算法因在复杂环境中的跟踪精度和实时性具有良好性能，逐步成为视频跟踪算法的重要研究方向。

2010 年，Bolme 等[7]首次将信号相关性和傅里叶时频域转换引入视频目标跟踪中，提出误差最小平方和滤波器（Minimizing the Output Sum of Squared Error，MOSSE），奠定了相关滤波视频目标跟踪算法的基础。之后的几年中该算法得到了迅速的发展，Henriques等[8]针对MOSSE 中滑动卷积的样本重复采样问题，引入循环矩阵，提出核循环算法（Circulant Structure of trackingby-detection with Kernel，CSK），并结合多通道方向梯度直方图（HOG）进行特征融合提出了核相关滤波（Kernelized Correlation Filters，KCF）算法；Danelljan 等[11]基于CSK提出了基于自适应颜色属性（Color Names，CN）的视频跟踪算法，有效解决跟踪过程中由复杂背景导致的目标定位不准确的问题。以上方法具有较好的跟踪效果和跟踪稳定性，但在复杂场景中的跟踪效果并不理想。

针对尺度变化问题，Danelljan等[9]以MOSSE算法为基础，提出多尺度空间滤波跟踪算法（Discriminative Scale Space Tracking，DSST）在此基础上为解决DSST跟踪速度慢的问题提出了快速的多尺度空间滤波跟踪算法（fast Discriminative Scale Space Tracking，fDSST）[10]，此方法虽能够较准确地估计目标的实时尺度，但缺乏对目标样本的学习和更新机制，对除尺度变化之外的其他复杂背景问题的跟踪效果不佳。在此基础上，Li等[16]引入七尺度的尺度池，能够解决模块大小定型的问题，并且融合HOG和CN特征来提升算法的整体性能。

针对复杂背景和遮挡跟踪问题，目前对大多数的改进集中于尽可能多地采集目标及目标周围特征，使得目标在跟踪的过程中能够获得目标的更大响应。Bertinetto等[17]融合HOG 和颜色特征，以DSST 方法估计目标尺度，提出了一种基于互补学习的跟踪方法（Staple），较高效解决了目标形变跟踪鲁棒性差，但融合特征计算量大且复杂，因此跟踪实时性偏低。Mueller等[18]在相关滤波的框架下，引入全局上下文信息来辅助定位目标位置，提出CA-CF（Context-Aware Correlation Filter）算法，该算法能够处理目标周围的边界响应问题，又能够较准确地跟踪目标位置。但由于提取的目标特征单一，因此对于跟踪遮挡目标效果较差。Zhang 等[19]在KCF 的基础上将多个特征进行融合，并引入多个核函数，训练多个位置滤波器，从而使得核有自适应选择的能力。还有如Ojala等[20]提出的局部二值模式（Local Binary Pattern，LBP），有计算量小、对噪声不敏感、对灰度和旋转具有不变性等优点，被应用于目标跟踪方法中[21]。

在复杂场景下核相关滤波及改进的跟踪算法在处理复杂场景下的视频序列时仍会存在一些问题，主要表现在：目标遮挡时，特征只能提取一部分，甚至不能提取到有效的目标特征；存在尺度变换和背景杂波时，固定的尺度大小容易提取到背景复杂时的非目标特征噪声，从而引起跟踪漂移、丢包等错误。

本文以KCF 算法为基础，针对相关滤波器在目标遮挡、尺度变换、背景杂波等复杂场景下跟踪效果不佳的问题进行改进，首先引入位置滤波器，分别提取HOG和CN特征并进行线性加权融合，估计目标中心位置，再引入尺度滤波器，估计目标尺度变换，用相关能量平均峰值判断目标是否被遮挡，当目标被遮挡时，用卡尔曼滤波根据目标历史路径数据估计出被遮挡时的目标位置。AMFKCF算法能够较好地解决上述复杂场景下跟踪效果不佳等问题，且兼具有核相关滤波算法的优点。

1 核相关滤波算法

核相关滤波目标跟踪算法[12]使用循环矩阵训练滤波器，并通过核函数预测目标位置。该算法包括目标特征循环采样、训练位置滤波器、预测位置及更新参数等过程。

1.1 目标特征循环采样

KCF 算法中，首先对初始化目标框进行一次采样，其他目标样本由循环偏移产生如图1所示，以目标位置的1.5～2 倍的矩形区域进行一次样本采样，记为s1，循环偏移产生目标样本记为s1=[ s1,s2,…,sn] ，然后通过循环矩阵N 对样本进行循环移位，若循环移位一次记为s2=N2s1=[ sn,s1,s2,…,sn-1] ，则循环移位的所有样本集合可表示为：Si+1=Ni+1*s1，i=1,2,…,n-1，Ni为N的第i 行元素，循环矩阵N 为：

图1 循环移位

1.2 训练滤波器

KCF算法以岭回归方式训练滤波器，其目标是寻找一个目标分类器f(w)=wTv(S)，使得滤波器期望输出yi和样本Si之间的均方误差函数最小，即：

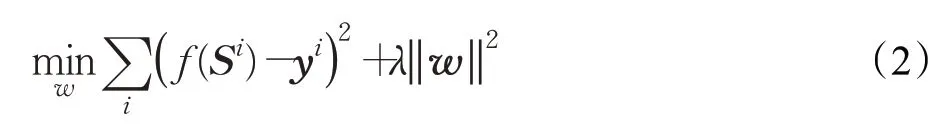
式中，Si、yi分别表示第i 个训练样本和期望输出，λ 为防止过拟合的正则化参数[22]，v(S)为Si的高维空间映射。若能找到一个目标分类器f(w)使得式（2）最小，则可以达到训练滤波器的目的。

当引入的图像块为多通道特征（如本文用HOG 和CN 特征进行融合）时，此时图像块映射v(S)为非线性函数，引入一个核函数，对图像块进行核化、对偶，记为a，则目标分类器内核函数就可表示为w=vTa，将其代入目标函数式（2）中，通过学习可得对偶空间系数a=(K+λI)-1y，其中K=vvT为核矩阵，K 为循环矩阵，因此对其进行离散化傅里叶变换可得分类函数的频域解，即：

式中，Kvv为样本向量Si之间的核相关向量。

1.3 预测位置及更新参数

式中，z 为下一帧待检测目标块，其检测对偶域求解公式为f( z;a )=aTvsv( z )；vs表示更新后的模型参数；采用与1.2节相同的方式求解目标块z 的所有循环移位的响应值，并计算滤波器频域响应表示相邻帧之间的快速傅里叶变换，再通过傅里叶反变换，得到最大响应点即为目标中心位置。

因目标外观、背景、所处环境的不断变换，所以跟踪过程中滤波器的相关参数也在不断地更新，核相关滤波算法的更新参数为对偶空间系数和图像模块ˆ，更新策略为：

2 自适应融合多特征的抗遮挡核相关滤波算法（AMFKCF）

在背景杂波、尺度变换、目标遮挡等复杂场景中，核相关滤波算法容易发生目标跟踪丢失。实时地提取、融合目标图像块的多个特征，估计、更新目标尺度的变化，将会有效地提高目标的跟踪性能。本文算法流程如图2所示。首先提取目标图像块的方向梯度直方图（Histogram of Oriented Gradient，HOG）[23]和颜色（Color Name，CN）[11]特征，并将两类特征进行融合，然后利用多个尺度池估计目标的尺度大小，再利用卡尔曼滤波器对目标的位置进行补偿，最后更新位置参数和尺度参数。本文算法的五个步骤：多特征融合、尺度计算、遮挡判别、卡尔曼位置滤波器补偿、滤波器参数更新。

2.1 HOG和CN特征融合

HOG 是通过计算、统计目标图像块的梯度方向直方图来构成目标的特征，具有图像几何和光学形变的不变性；CN 是通过提取目标块RGB 空间的3 维颜色特征映射到黑、蓝、棕、灰、绿、橙、粉、紫、红、白和黄的11 维颜色空间，对不同颜色物体进行分离，对颜色区别显著且纹理形状相似的目标和背景具有很好的区分度，CN颜色特征具有旋转、平移和尺度不变性的优点。HOG和CN特征具有一定的互补性，二者提取的算法相对简单，对实时跟踪效果影响小，因此本文选取这两种特征进行融合。

提取HOG和CN特征采用31和10维通道来描述目标，因此融合后的特征维数为41维，设HOG和CN特征分别为：

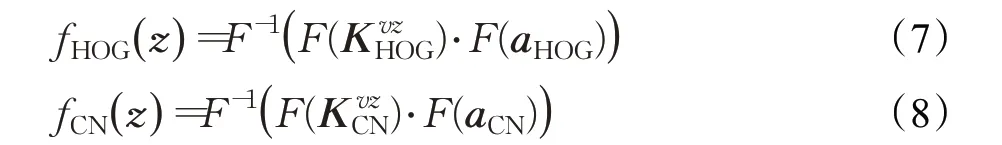
式中，aHOG和aCN分别为HOG 和CN 对应的特征训练相关滤波器，和分别表示多通道特征的的训练样本ν 与预测区域z 之间的核相关，F()⋅和F-1()⋅分别表示傅里叶变换和傅里叶逆变换。通过线性加和的方式融合多通道特征，即：

式中，βHOG、βCN为HOG和CN特征响应融合权值。方便起见，取值βHOG=0.5，βCN=0.5。

2.2 利用目标尺度池计算尺度

在跟踪目标的过程中，目标的尺度实时变化，因此固定跟踪框大小的算法跟踪效果往往不理想，无法准确地跟踪目标。因此本文加入了尺度滤波器估计目标尺度。

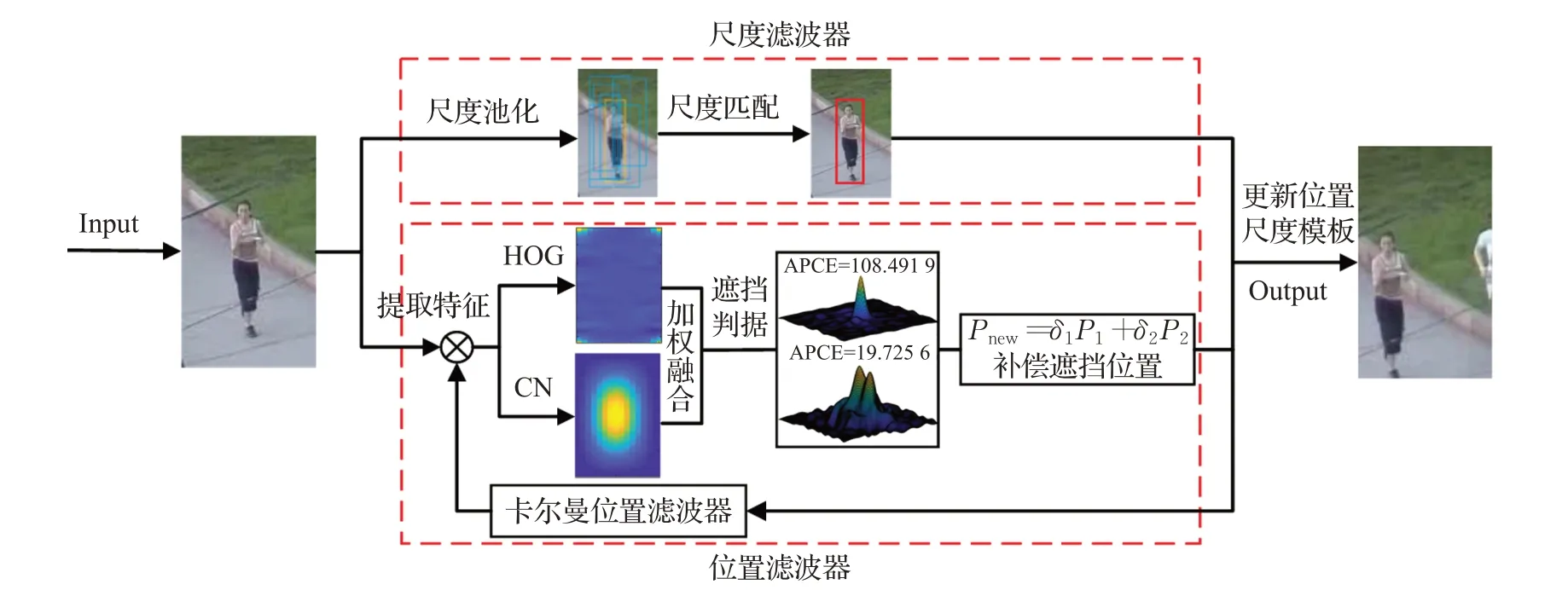
图2 AMFKCF算法流程

假设P×M 为基础图像块大小，则目标尺度池可表示为：

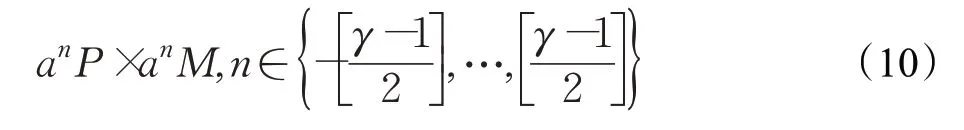
其中，P、M 分别表示上一帧目标的高度和宽度，a=1.02 为尺度因子，γ=33 为尺度池图像块个数。

帧数大于2 时，首先核相关滤波器计算新位置，在上一帧尺度的基础上利用尺度滤波器，以当前新位置获取不同尺度的图像池，从而找到最匹配的尺度。计算可参考文献[12]。

2.3 遮挡判别

在目标跟踪的过程中，抗遮挡算法一直以来都是研究的热点，本文引入Wang等[24]提出的平均峰值-相关能量（Average Peak-to Correlation Energy，APCE）遮挡判据。APCE的定义公式如式（11）：

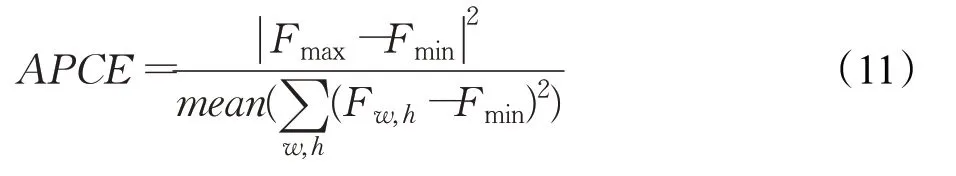
式中，Fmax、Fmin和Fw,h分别为f(z)的峰值、谷值及位置(w,h)对应的响应值，mean(⋅)为求平均值。

该判据可以反映出响应图的振荡程度，如图3 所示，当目标没有发生遮挡时，响应图只有一个尖锐的峰和平滑下降的区域，APCE 变得更大，当目标被遮挡或消失的时候，APCE 将会急剧下降，响应图会存在多峰和凹凸的区域。当Fw,h响应值峰值大于δ1和响应值均值的乘积，同时当前位置的APCE 值F(w,h)|APCE也大于δ2和目标位置的APCE历史均值的乘积时，目标没有发生遮挡，此时下式成立：

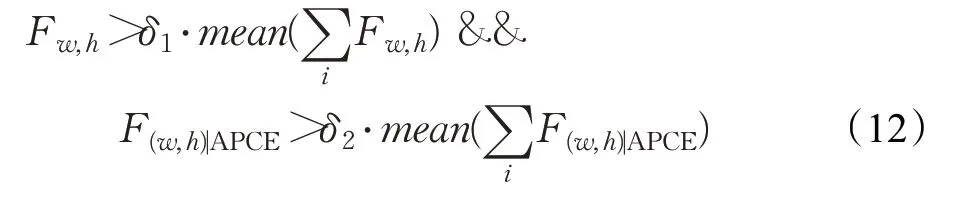
2.4 卡尔曼位置补偿滤波器

在目标轨迹跟踪方面卡尔曼滤波（Kalman Filter）发挥重要作用[25-27]，通过系统输入输出观测数据对系统状态进行最优估计，尤其适用于目标遮挡情况。假设目标的状态向量为，观测向量为zk=[ x,y]T,其中x、y 为目标位置分量，˙为目标速度分量。因此跟踪物体的运动状态方程为：

其中，xk和zk分别为第k 帧目标的状态和观测值，Ak是状态转移矩阵，Hk是观测矩阵，过程噪声wk和观测噪声vk为协方差分别为Qk和Rk的高斯白噪声。通常目标在相邻两帧的运动状态可以看作匀速直线运动，所以Ak和Hk定义为：

除了传统色彩浓厚外，蒋介石的意识形态建构崇尚军事化，这与其早年在日本所受严格的军事训练及他本人对日本社会的观感有很大关系。蒋介石认为日本之所以骤致富强，与武士道精神有密切关系。蒋介石在新生活运动中提倡社会军事化，以军事化的标准来改造社会。与其长期以来对党组织的失望和嫌恶相比，蒋介石对于军人和军队组织的美德赞誉有加。而崇尚军事化的意识形态宣导窒息了社会的活力和能动性，为实现僵化的统制，放弃了意识形态的社会动员功能。

式中，Δt 表示相邻两帧采样时间间隔。如视频序列每秒采样n 次，则Δt=1/n。

Kalman算法一般包括预测和更新两个步骤。预测步骤为：

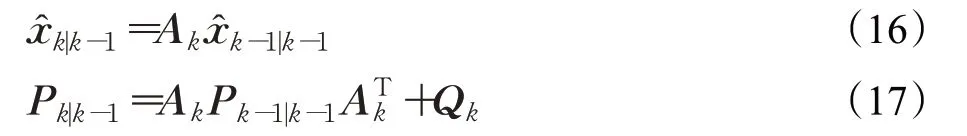
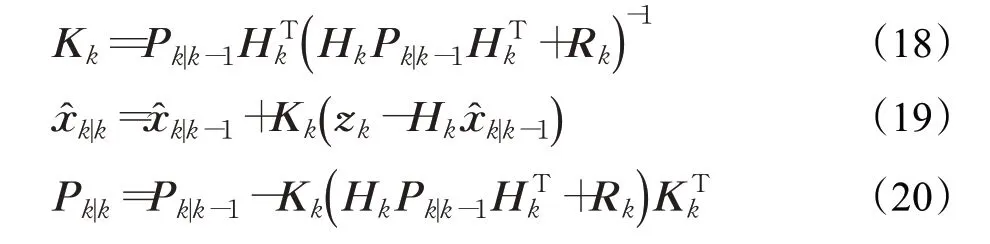
其中，Kk为卡尔曼增益，为k 时刻的状态最优估计结果，Pk|k为k 时刻的状态估计的协方差。

从第2帧开始对目标的位置进行预测，通过位置滤波器式（4）计算出的未修正目标位置为，因此卡尔曼滤波器补偿目标位置策略为：式中，δ1、δ2为位置补偿权值，[ x,y] 为卡尔曼滤波器预测的位置，本文中当APCE 判据判断未发生遮挡时δ1=0.99、δ2=0.01；发生遮挡时δ1=0.01、δ2=0.99，此时卡尔曼滤波器充当位置滤波器，估计目标位置。

2.5 模板参数更新

模板更新包括尺度模板和参数模板更新，当获得的最优尺度SPM与模板尺寸对应的对偶空间系数aPM-1之间采用线性加权法来更新第t+1 帧的目标尺度模板：

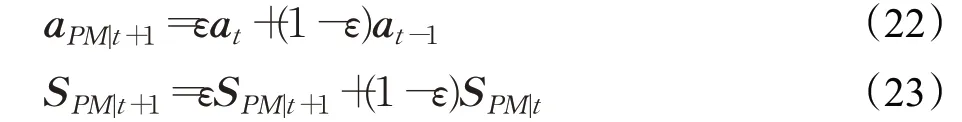
式中，ε 为尺度模型更新学习率，本文设为0.025。

图3 遮挡与未遮挡时APEC值

3 实验仿真与结果分析

本文选取具有目标形变、遮挡、尺度变换、运动模糊、平面旋转、光照变换、背景杂波等特性的图像序列，与KCF[12]、CACF[18]、CN[11]、CSK[8]、DSST[9]、CXT[28]、CT[29]、DFT[30]等经典算法在CVPR2013 Benchmark[31]数据上进行对比。为了综合地评价各个跟踪算法的性能，选取5个常用目标跟踪评估指标[32]分别为：中心位置误差（Center Location Error，CLE）、距离精度（Distance Precision，DP）、每秒运行帧数（Frames Per Seconds，FPS）、一次通过评价（One-Pass Evaluation，OPE）所计算的成功率和精确度。

实验软件环境为MATLAB R2018a，硬件环境为：Intel Core i5-5200U处理器，2.20 GHz主频，4 GB内存，Windows 10操作系统。

3.1 中心位置误差

中心位置误差是跟踪目标精度的一个评估指标，是目标跟踪框中心位置和实际目标跟踪框中心位置之间欧式距离的均值。CLE值越小，跟踪结果越准确。表1是各算法跟踪图像序列的CLE结果，每个图像序列最优的CLE 加粗，次优用斜体标注。在表1 中，本文算法（AMFKCF）有11 个最优中心位置误差，12 个次优的中心位置误差。AMFKCF算法的平均CLE为10.85像素，相比于基础算法KCF的平均CLE（25.52个像素）提高了14.67个像素，故AMFKCF算法的平均CLE均优于其他6种跟踪算法。

3.2 距离精度

距离精度是跟踪目标中心位置误差小于一定阈值的帧数和总帧数的比值。DP 值越大，表示跟踪结果越准确。表2 是各种算法跟踪图像序列的DP 结果，每个图像序列最优的DP 加粗，次优斜体标注。本文算法（AMFKCF）的平均DP 是90.81%，比基础算法（KCF）的平均DP（81.06%）提高了9.75个百分点，比MOSSE_CA的平均DP（55.94%）提高了34.87 个百分点，比CN 的平均DP（68.91%）提高了21.9个百分点，比CSK的平均DP（65.94%）提高了24.87个百分点，比DCF_CA的平均DP（87%）提高了3.81 个百分点，比DSST 的平均DP（84.74%）提高了6.07 个百分点，故AMFKCF 算法的平均DP均优于其他6种跟踪算法。

表1 中心位置误差（CLE） 像素

表2 距离精度（DP） %

3.3 每秒帧数

每秒运行的帧数是跟踪算法每秒处理图像序列的帧数，是衡量算法跟踪速度的标准之一。FPS 的值越大，代表算法处理图像序列速度越快，表3 是各种算法跟踪图像序列的FPS，每个图像序列最优的FPS 加粗，次优斜体标注。虽然本文算法（AMFKCF）的FPS 和KCF 的FPS 相比有所降低，但是速度相比于经典算法DSST还是略高，基本满足实时性。

3.4 成功率图和精度图

本文采用OPE 评价标准计算的成功率图和精度图来进一步分析AMFKCF 算法和其他9 个跟踪算法的跟踪性能，OPE是指跟踪算法按照视频序列的顺序来处理每帧的视频序列。精确度是指中心位置误差在给定阈值范围内的帧数和总帧数的比值，图4的精确度曲线图的阈值范围为0到50。成功率表示的是给定一个阈值，计算跟踪目标位置和真实目标位置的重叠率，重叠率定义为：

其中，rt是跟踪目标框，rs是真实目标框，| |⋅是目标框内的像素点数目。

估计图像序列中目标位置和实际目标位置的重叠率S 大于给定阈值的图像序列帧数与总图像序列帧数的比值即是成功率。成功率图采用曲线下面积（AUC）的值来衡量算法性能，阈值范围是0到1，AUC代表跟踪目标成功率的大小，AUC 越大，跟踪目标的成功率越大。图4 的精确度图中本文算法（AMFKCF）的精确度是0.959，比第二名DSST 算法精确度（0.898）高0.061，比KCF精确度（0.844）高0.115。图5成功率图中AMFKCF成功率是0.659，比第二名DCF_CA 算法成功率（0.613）高0.046，比KCF成功率（0.576）高0.083。

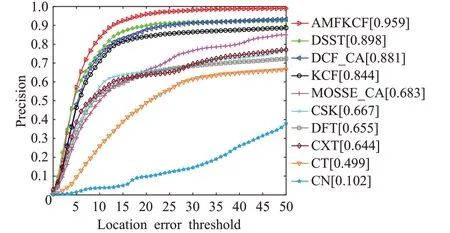
图4 精确度图

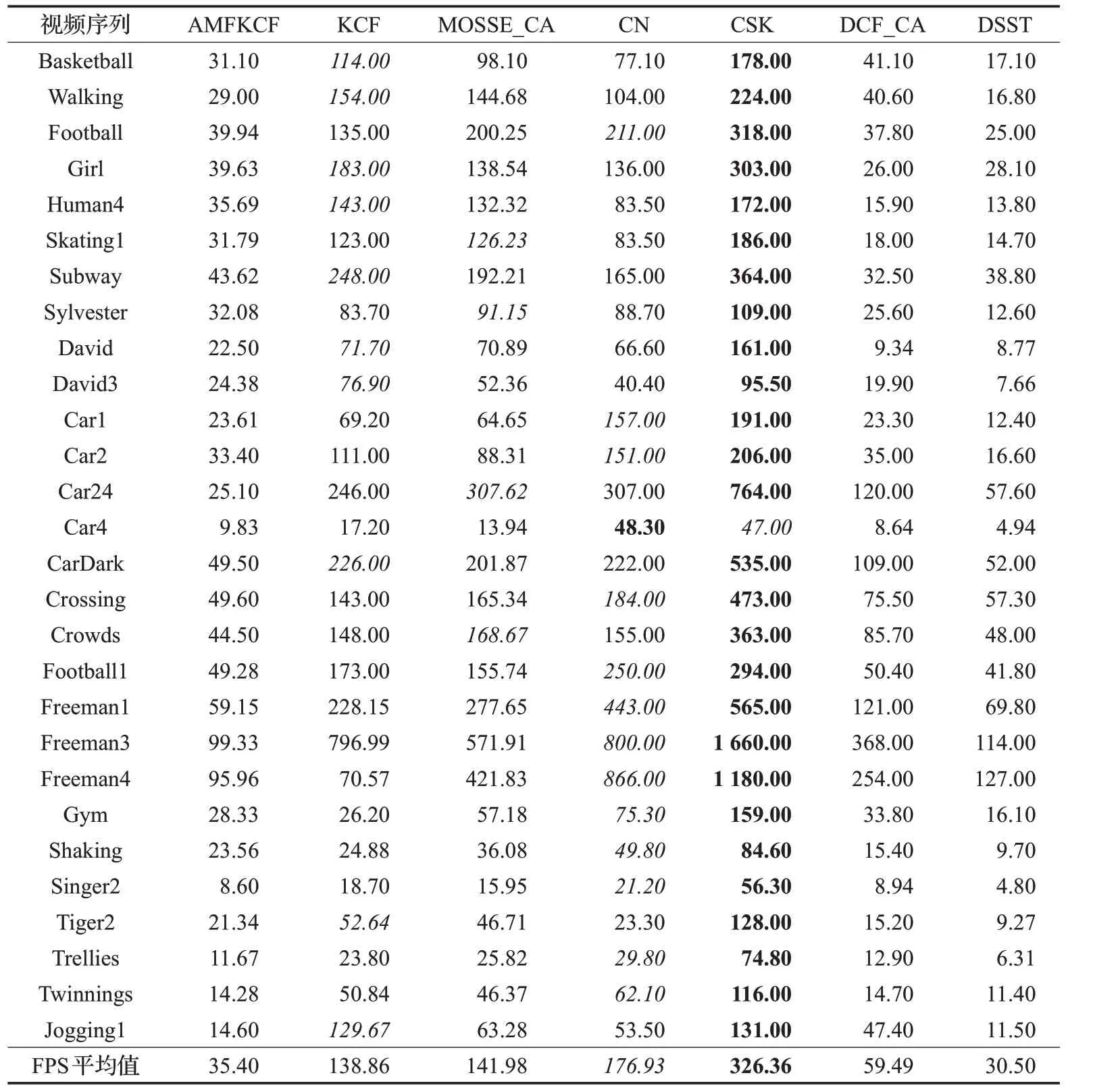
表3 每秒帧数（FPS）

图5 成功率图

为了全面准确地分析本文算法（AMFKCF）在各种复杂场景下的性能，图6是AMFKCF和其他9种跟踪算法对24个具有不同属性具有挑战性的图像序列进行跟踪所得到的精确度图和成功率图。从图中可以看出，AMFKCF在处理背景杂波、平面旋转、形变、严重遮挡、尺度变换、光照变换等属性的视频序列时跟踪精度和成功率均优于其他算法，只有跟踪具有光照变换属性的视频序列，AMFKCF 的跟踪精度和成功率相比于有些算法性能略差。

为了直观说明本文算法（AMFKCF）跟踪的准确性，图7 给出了AMFKCF 和9 种主流算法跟踪视频序列cardark、david、david3、dog1、faceocc2、girl、jogging1、shaking、treilles、walking1、woman 的结果。在图7（a）cardark 截取的部分跟踪结果图中，AMFKCF 的跟踪框一直准确地跟踪着目标车辆，并随着车辆在视频序列中的尺度大小变换而变换。图7（b）是david部分视频跟踪结果，在#0569帧中，目标尺度变大，AMFKCF算法跟踪框也随着变大，在#0696帧中，视频中人摘掉眼镜，目标尺度变大，AMFKCF算法跟踪框随着变大，并准确跟踪上。图7（c）是david3 部分视频跟踪结果，#0032 帧视频中的人从电线杆后面经过，#0092 帧中人经过树，#0200帧人往回来走，再次经过树，#0243帧再次经过电线杆，面对严重遮挡，AMFKCF 算法能够很好地跟踪上视频中的行人。图7（d）是dog1 部分视频跟踪结果，视频中玩具狗的尺度在#0264 帧、#0550 帧、#0740 帧、#0937 帧都有明显的尺度变换，AMFKCF 算法的跟踪框也随着发生了较为明显的尺度变换。图7（e）是faceocc2 的部分视频跟踪结果，视频中男士在#0026 帧、#0151 帧、#0263 帧、#0570 帧视频序列中均有明显尺度变换，在#0263帧、#0489帧、#0570帧男士的面部有了一些遮挡，但是AMFKCF算法的跟踪框一直能够准确地跟踪上目标。图7（f）是girl的部分视频序列，在#0038帧、#0173、#0310帧，视频序列中的女孩面部有明显的旋转，AMFKCF算法跟踪框一直能够跟踪上，在girl 中的女孩面部有尺度变换，AMFKCF 算法可以很好地处理。图7（g）是jogging1的部分视频序列，从#0073帧、#0084帧，视频序列中的女孩经过电线杆的遮挡，AMFKCF 算法的跟踪框还是能跟踪上目标。图7（h）是shaking的部分视频序列，视频序列中的歌手站在舞台上，有明显的光照变换和尺度变换，跟踪框一直能够跟踪上目标。图7（i）是treilles的部分视频跟踪序列，图中的视频序列中的人物处在很暗的环境下，并且有些尺度变换，AMFKCF算法仍能跟踪上目标。图7（j）是walking1的部分视频序列，#0018 帧、#0089 帧、#0121 帧视频序列中的人经过电线杆，还是能够在严重遮挡情况下跟踪上目标。图7（k）是woman的部分视频序列，在#0125帧、#0205帧、#0323帧中的女士均发生严重遮挡，到#0392帧AMFKCF能够准确跟踪上目标。

图6 复杂场景下的精确度、成功率图

图7 部分视频序列跟踪结果

4 结语

本文提出一种结合卡尔曼滤波的多特征融合的尺度自适应相关滤波算法，算法中有位置和尺度滤波器，在KCF 的框架上得到两个特征的响应值，并进行线性加权融合，融合后的响应值来确定目标的位置；在此基础上，引入了尺度滤波器来估计目标的尺度，以此来增强尺度的自适应能力；但是在面临严重遮挡问题时还会出现跟踪目标丢失的现象，所以本文再引入卡尔曼滤波，对跟踪目标的位置进行修正来保证跟踪结果的精确性。为了验证本文算法（AMFKCF）算法的综合性能，AMFKCF 和9 种经典算法同时处理具有不同属性的图像序列，结果表明，AMFKCF算法处理遮挡、尺度变换、背景杂波、形变、平面旋转等具有挑战性的场景时，在保证速度的同时跟踪精确度也表现良好。

AMFKCF 算法在处理大多数具有挑战性场景的视频序列时都能表现出良好的性能，而且基本满足实时性，但是在跟踪具有运动模糊属性的视频序列时跟踪性能稍弱，因此未来工作将基于AMFKCF 算法在处理运动模糊方面做出改进。