利用自然最近邻的不平衡数据过采样方法

孟东霞，李玉鑑

1.河北金融学院 金融科技学院，河北 保定071051

2.桂林电子科技大学 人工智能学院，广西 桂林541004

在不平衡数据中，各类别样本的数量存在较大差异，样本数量较多的类被称为多数类，样本数量较少的是少数类。不平衡数据集在信用风险评估、欺诈检测、疾病诊断、气象预测等应用领域中广泛存在，其中的少数类样本是识别的重点，若被误分类将带来重大的损失。以信用评估问题为例，信用差的客户样本相对较少，传统分类算法在对其进行分类时，侧重于考虑整体分类准确率，易造成少数类的误判，导致少数类的信用差的客户被误分为好客户的错误率较高，若给其拨付贷款，将给企业造成极大的资金损失。因此，有效提高不平衡数据集的分类性能是目前的研究热点。

目前，针对不平衡数据的研究主要有算法层面和数据层面两种思路：算法层面主要通过引入误分类代价、集成学习等手段使分类算法更侧重于少数类，包括代价敏感学习方法、提升算法和集成算法；在数据层面上，常用过采样、欠采样和混合采样三种方式改善样本分布，再对获得平衡的数据集进行分类。过采样通过某些策略增加少数类样本的个数；欠采样通过剔除部分多数类样本，减少多数类样本的个数；混合采样将过采样和欠采样相结合使各类样本数量接近。本文将从数据层面通过增加少数类样本的数量对不平衡数据进行处理。

随机复制少数类样本虽然能快速直接地增加样本数量，但实际效果不够理想，易产生过拟合[1]。SMOTE算法（Synthetic Minority Over-sampling Technique）是目前最为典型的过采样方法，其通过对少数类样本和K个近邻插值合成新样本，以增加少数类样本的数量[2]。SMOTE算法虽然在一定程度上改善了少数类样本的分类性能，但是未考虑到少数类样本类内不平衡的情况，易引入噪声点。Borderline-SMOTE（Borderline Synthetic Minority Over-sampling Technology）根据少数类样本点周边的近邻分布，将其分为safe（近邻均为少数类样本）、danger（近邻中包含少数类和多数类样本）和noise（近邻均为多数类样本）三种类型，只选取danger样本利用SMOTE 算法合成新样本，通过强化边界点的影响力来提高分类性能[3]。基于聚类的过采样方法先对少类样本进行聚类，然后在每个类簇中生成特定数量的新样本，避免生成跨越边界的噪声点，聚类方法包括Kmeans聚类[4]、层次聚类[5]等策略。带多数类权重的过采样方法根据少数类和多数类样本的距离信息，识别出难以学习的、加权信息量较大的少数类样本，结合其所属的少数类类簇合成新样本，有效减少了重叠新样本的生成[6]。周等人提出的基于样本分层的双向过采样方法基于最高密度点和类内距离将少类样本分为密集层和稀疏层，在两者之间进行双向过采样，避免了采样后类内样本分布不均的问题[7]。考虑到支持向量对分类超平面的影响，基于支持向量的过采样方法在利用支持向量机训练完数据集后，使用支持向量生成新的少数类样本[8]。针对少数类样本可能存在的类内不平衡和新生成样本的重叠问题，本文基于自然最近邻的定义和分布特征设计了一种结合少数类样本自然近邻关系和内部类簇信息进行过采样的不平衡数据处理方法。所提方法首先根据自然最近邻的定义计算少数类样本的自然最近邻，获得处于样本分布密集区域中的核心点，然后基于自然近邻关系对少数类样本进行聚类，最后利用同类中的核心点和非核心点合成新样本。

1 自然最近邻

自然最近邻是近年来提出的最近邻概念，其在离群点检测[9-10]、数据聚类[11-12]和协同过滤[13]等领域中的应用具有良好的表现，其考虑到了样本分布疏密程度对近邻个数和对称关系的影响，即密集区中的样本点拥有较多的自然近邻，稀疏区的样本点近邻较少，离群样本点和噪声点的近邻相对很少甚至为0。自然近邻的搜索无需人工指定参数，根据每个点的分布特征自适应生成，当所有样本点都有逆近邻或逆近邻个数为0 的所有样本不变时结束，达到自然稳定状态[14]。

假设有数据集X={ x1,x2,…,xn} 。

定义1（最近邻）NNr( xi)表示样本点xi的r 最近邻，r 由自然最近邻搜索算法自动产生。

定义2（逆近邻） RNNr( xi)表示样本点xi的r 逆最近邻：

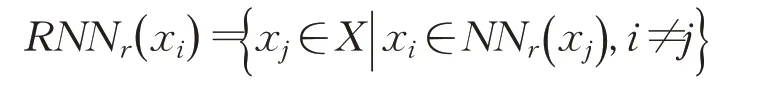
定义3（自然最近邻） NNN( xi)表示样本点xi的自然最近邻：

由定义3 得出，自然最近邻是一种对称的邻居关系，即样本点xi和xj互为彼此的r 近邻。

定义4（自然稳定状态）当所有的样本点都有逆近邻或者逆近邻个数为0的样本点不变时，自然近邻搜索过程到达自然稳定状态。到达自然稳定状态时的搜索次数称为自然特征值，记为supk。

算法1描述了自然最近邻搜索算法的具体步骤。

算法1 自然最近邻搜索算法

输入：数据集X 。

输出：supk,NNN( xi)，自然近邻数NB( xi)。

步骤1 初始化搜索次数r=1,NB( xi)=0,NN( xi)=∅,逆近邻RNN( xi)=∅。

步骤2 计算xi的r 近邻，更新NB( xi)、NN( xi)、RNN( xi)。

步骤3 r=r+1。

步骤4 当所有xi的RNN( xi)≠∅或{xi|RNN( xi)=∅} 不再变化时，搜索过程到达自然稳定状态，supk=r-1，否则转至步骤2。

步骤5 计算所有样本的自然最近邻，NNN( xi)=NN( xi)⋂RNN( xi)，输出supk、NNN( xi)和NB( xi)。

通过算法1 可以看出自然特征值supk是所有样本的自然邻居数量的平均值，自然邻居数大于等于supk的样本点位于样本分布密集区，其余样本点的分布较为稀疏。

2 基于自然最近邻的过采样方法

针对少数类样本类内不平衡、新生成样本存在噪声和重叠的问题，本文设计了一种结合少数类样本的自然近邻关系和所属内部类簇进行过采样的不平衡数据处理方法。所提方法首先根据自然最近邻的定义计算少数类样本的自然最近邻，获得处于样本分布密集区域中的核心点，然后基于自然近邻关系对少数类样本进行聚类，最后利用同类中的核心点和非核心点合成新样本。

2.1 少数类基于自然最近邻的聚类

依据算法1 对少数类样本完成自然最近邻的搜索过程后，参考文献[15]基于自然近邻关系对少数类样本进行密度聚类，过程主要包括三个步骤：首先根据所有少数类样本的自然近邻关系确定核心点；计算核心点的自身邻域半径，确定与其密度直达的核心点，依据密度聚类的过程对核心点聚类，将互相处于自身邻域半径值范围内的两个核心点归为同一类；依据非核心点和核心点的近邻关系，将非核心点划归到现有分类中。

定义5（核心点）对于xi∈X ，若满足NB(xi) ≥则称xi为核心点。核心点的自然近邻数NB( xi)不小于自然特征值supk，且大于其所有自然近邻的自然近邻数的平均值，位于样本分布的密集区域中。

定义6（邻域半径） xi的邻域半径εi是xi到所有自然近邻的最大距离，即

定义7（直接密度可达）若样本点xi与xj之间的距离D( xi,xj)满足D( xi,xj)≤εi和D( xi,xj)≤εj，则称xi与xj直接密度可达。

密度相连、密度可达的定义与密度聚类算法中的定义相同。

算法2 少数类基于自然最近邻的聚类算法

输入：少数类样本的supk，NNN( xi)和NB( xi)。

输出：少数类样本的核心点集合C_set ，非核心点集合NC_set，聚类个数K 和各类簇的样本集合CK。

步骤1 根据定义5，由supk、NNN( xi)和NB( xi)确定C_set 和NC_set。

步骤2 对xi聚类，xi∈Cset。

步骤2.1 根据定义6 和7，计算xi的邻域半径εi和直接密度可达的核心点集合DRi。

步骤2.2 利用εi和DRi，参照密度聚类的流程，将所有密度相连的核心点归入同一个类簇，得到CK和K。

步骤3 将xj划分到K 类中，xj∈NCset。

步骤3.1 计算xj的εj。

步骤3.2 得到与xj互为自然近邻且彼此互在对方邻域半径内的所有核心点。

步骤3.3 确定距离xj最近的核心点xi，将xj加入xi所在的类簇中；若不存在这样的核心点，则将xj标记为噪声点。

新样本由属于同一类簇中的核心点和非核心点生成，噪声点不参与样本点的合成，可避免引入新的噪声点。

2.2 基于自然最近邻的过采样方法

对少数类样本完成聚类操作后，根据各类中的非核心点所占比例确定各个类需合成的样本个数，类内非核心点越多，需合成的新样本越多。原因在于非核心点是自然近邻数小于自然特征值的样本，其周围的样本分布较为稀疏，在其内部更多地合成新样本，可避免新样本过多地集中于分布密集的区域中，减少了合成样本的重叠。算法3 描述了基于自然最近邻进行过采样的具体步骤，流程图如图1所示。

算法3 基于自然最近邻的过采样方法

输入：不平衡数据集S。

输出：过采样生成的少数类样本集合Sgen。

步骤1 使用算法1 对少数类样本进行自然最近邻的搜索，得到supk、NNN( xi)和NB( xi)。

步骤2 根据算法2 对少数类样本进行聚类，得到K、CK、C_set、NC_set。

步骤3 新合成的样本数N=多数类样本数-少数类样本数。

步骤4 计算类Ci中非核心点的比例ρi，按照比例大小确定类Ci需合成的样本数

步骤5 在类Ci中随机挑选非核心点x 和核心点y合成新样本，i=1,2,…,K 。 z=x+a×( y-x )，a 是[0，1]之间的随机数，将z 加入集合Sgen。重复进行此步骤直到各类获得所需样本数。

Sgen即为合成的少数类样本集合。

2.3 算法时间复杂度分析

假设在不平衡数据集中，少数类样本个数为nmin，多数类样本个数为nmax。本文方法的时间复杂度由以下主要步骤决定：

图1 基于自然最近邻过采样方法的流程图

（1）搜索所有少数类样本的自然最近邻：①创建可用于存储数据的KD 树，时间复杂度为O( nminlb nmin)；②每一轮搜索自然最近邻，时间复杂度为O( nminlb nmin)，共进行supk轮，时间复杂度为O( supk×nminlb nmin)，由于大量实验表明supk远小于nmin，一般在[1，30]之间，因此，该步骤的时间复杂度为O( nminlb nmin)。

（2）对少数类样本进行聚类：①依据定义5，将样本分为核心点和非核心点，时间复杂度为O( nmin×supk)，由于supk远小于nmin，可记为O( nmin)；②使用密度聚类对核心点聚类，假设核心点数量为nmin_c，使用KD树加快索引，时间复杂度为O( nmin_clb nmin_c)；③将非核心点划分到K 类中，假设非核心点数量为nmin_nc，通过之前保存的自然近邻信息，时间复杂度为O( nmin_nc)。该步骤的时间复杂度为O( nmin+nmin_clb nmin_c)。

（3）在各类簇中合成新样本：①计算各类簇的新生成样本数，时间复杂度为O( K )；②在各类簇中生成新样本，时间复杂度为O( N )，N=nmax-nmin，为新生成样本数。该步骤时间复杂度为O( N )。

将上述步骤的时间复杂度相加并化简，得到本文方法的时间复杂度为O( nminlb nmin+nmax)。

实验部分用到的SMOTE、Borderline-SMOTE 和SVM过采样方法的时间复杂度如表1所示。

表1 其他方法的时间复杂度

通过对比可以看出本文方法的时间复杂度与SMOTE 和Borderline-SMOTE 基本接近，优于SVM 过采样方法，证明了本文方法的有效性。

3 实验

3.1 人工数据集

为了验证本文所提方法的有效性，构造人工数据集比较不同过采样方法新生成样本的分布情况。假设所构造的数据样本点为( xi,yi)，其中xi是二维特征，其在两个维度上均服从均匀分布，yi是类标签。在图2 中，多数类由实心点表示，少数类是X 形，新生成的少数类样本由方块形表示，其数量是多数类样本和少数类样本的差值。在算法实现上，SMOTE 和Borderline-SMOTE方法使用的是Python库imbalance-learn package中的程序，所提方法使用python语言编写完成。

图2 给出了不同过采样方法合成新样本的分布图。图2（a）中是数据的原始分布情况，多数类中包含少量的少数类样本噪声点；图2（b）和（c）分别是采用SMOTE 和Borderline-SMOTE 方法合成的样本分布情况；图2（d）展示了本文方法所合成的新样本分布情况。通过对比可以看出，本文方法引入了较少的噪声点，生成的新样本较为均匀地分布在少数类的两个类簇中，重叠样本较少。

3.2 UCI数据集

为了进一步验证本文方法的有效性，利用SMOTE、Borderline-SMOTE、SVM过采样方法和本文方法对9组UCI数据集进行少数类样本的过采样处理，再使用支持向量机和KNN对采样后的数据进行分类。数据集信息如表2所示，不平衡率是少数类样本数量和多数类样本数量的比值。对于多类数据集，将其中一类设置为少数类，其余类合并为多数类。所有样本点的特征值都被缩放到[0，1]之间。采用五折交叉验证的方法将所有数据集分为训练集和测试集，取平均值作为实验结果。本文所提方法使用Python 语言编写，SMOTE、Borderline-SMOTE和SVM过采样方法使用的是Python库imbalancelearn package 中的代码。支持向量机、KNN 都使用Python库scikit-learn中的代码，SVM的核函数采用高斯核，KNN的近邻数量设置为5。

图2 不同过采样方法在人工数据集上的合成样本分布图

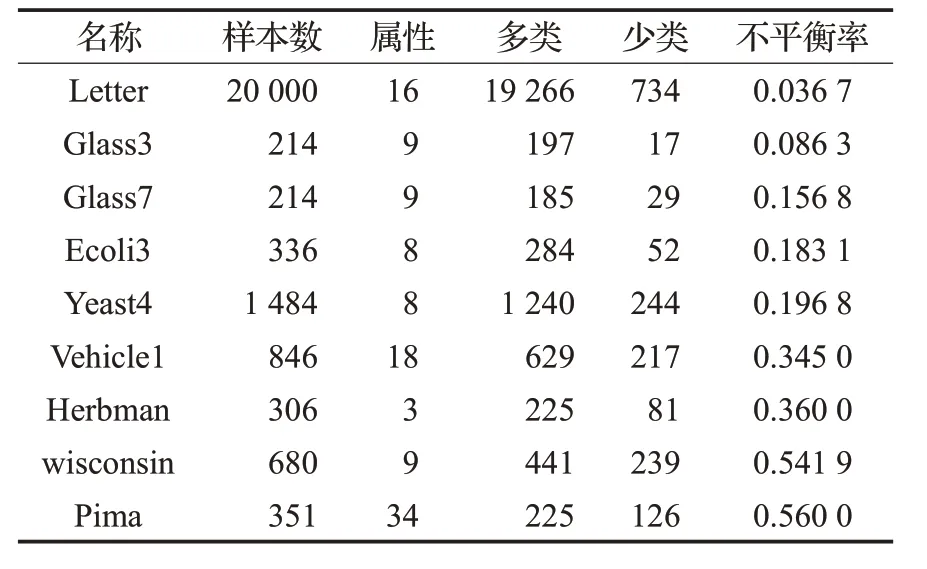
表2 实验所用数据集

本文选择不平衡数据分类问题的常用评价指标Fvalue、G-mean 和AUC 作为分类结果。其中，AUC 是ROC 曲线下各部分的面积之和，表示分类器将随机测试的正实例排序高于随机测试的负实例的概率，数值越大，分类性能越好。F-value 和G-mean 的计算过程由混淆矩阵构造得到。混淆矩阵的定义如表3所示。

表3 混淆矩阵

F-value：

G-mean：

G-mean 同时考虑了多数类和少数类的分类准确率，可用于衡量整体分类效果。

表4和表5给出了不同过采样方法处理后分别使用SVM、KNN 分类后得到的F-value、G-mean 和AUC 值，取得最优的数据使用黑色粗体标示。对每个评价指标，将四种不平衡处理方法在同一个分类器中得到的数值按照最优到最差排序，最优的序号为1，依次递增，在表格的最后一行给出四种方法在所有数据集中的平均排名，最佳排名使用黑色粗体标示。

通过对比实验结果可以看出：

（1）平均值排名。相较于SMOTE、Borderline-SMOTE和SVM 过采样方法，在本文方法处理得到的平衡数据集上，SVM、KNN 分类器都获得了较好的分类性能，指标F-value、G-mean 和AUC 的平均值排名都是最佳，证明所提方法对处理不平衡数据具有明显的优势。

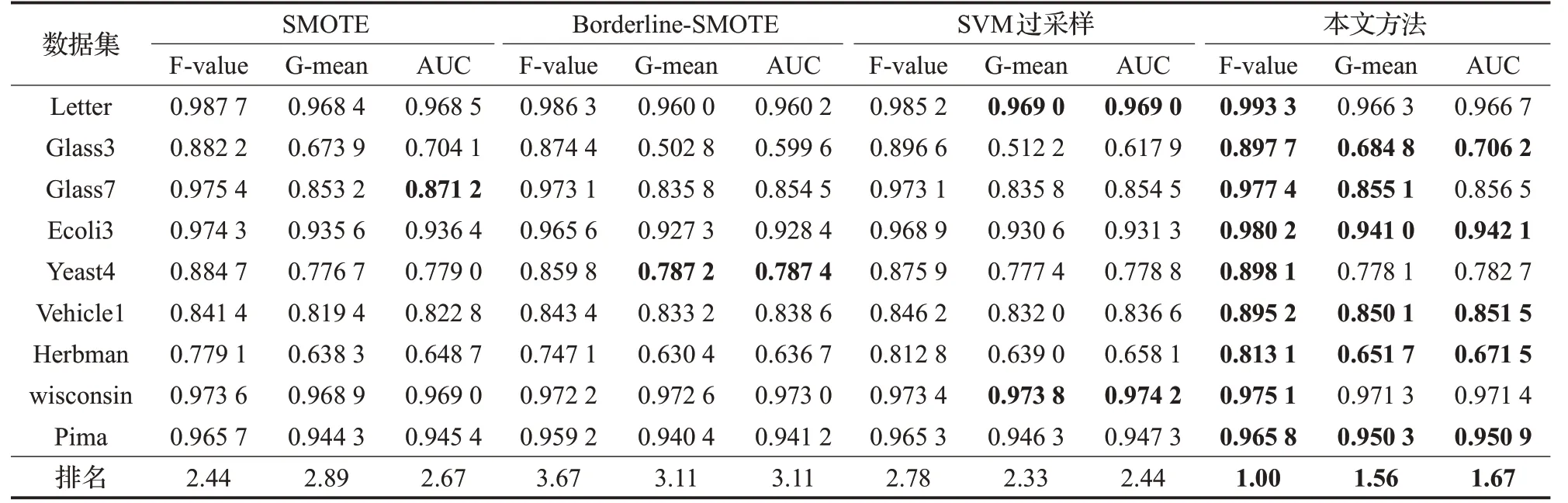
表4 SVM分类器实验效果对比

表5 KNN分类器实验效果对比

（2）F-value。在SVM的分类结果中，本文方法在所有数据集上都取得了最优值。在KNN 的分类结果中，本文方法在六个数据集中获得最优值，在数据集Letter、Glass7和Yeast4中的结果略低于最优值。总体来看，本文方法有效提高了少数类样本的分类准确率。

（3）G-mean 和AUC 值。在分类器SVM 和KNN 的分类结果中，本文方法在大多数数据集中都取得了最优值，证明所提方法改善了不平衡数据的整体分类性能。

（4）在数据集Glass3、Ecoli3、Vehicle1和Herbman上，本文方法同时取得了最优的F-value、G-mean和AUC值。

（5）原因在于本文方法考虑到了少数类样本中存在的类内不平衡问题，而其他方法未考虑到样本内部分布情况。

4 结束语

本文提出了一种基于自然最近邻过采样的数据处理方法。该方法首先计算所有少数类样本的自然最近邻，获得位于样本分布密集区域中的核心点，然后基于自然近邻关系对少数类样本进行密度聚类，最后选择同一类簇中的核心点和分布于稀疏区中的非核心点生成新样本。在人工数据集和UCI 数据集上开展的对比实验证明所提方法减少了噪声点和重叠样本的引入，有效提高了不平衡数据的分类性能。为了使新生成的样本更能体现少数类样本的分布特征，改进代表点的选择和合成策略将是进一步的研究方向。