结合密度峰值和切边权值的自训练算法
2021-01-22卫丹妮杨有龙仇海全
卫丹妮,杨有龙,仇海全,2
1.西安电子科技大学 数学与统计学院,西安710071
2.安徽科技学院 信息与网络工程学院,安徽 蚌埠233030
数据分类是机器学习领域的一个非常活跃的研究方向。传统的有监督分类方法为训练出有效的分类器,往往需要大量的有标记样本。但在实际应用中,有标记样本的获取需要付出较大的代价,不易获取,而无标记样本的获取相对较容易。因此,在有标记样本量较少时,有监督分类方法难以训练出有效的分类器。在这种情况下,只需少量的有标记样本,并充分利用大量无标记样本的半监督分类方法[1-2]引起越来越多的关注。自训练[3-4]是半监督分类中常用的方法之一。首先,用少量有标记样本训练一个初始分类器,并对无标记样本分类。然后,选择置信度较高的无标记样本及其预测标签,扩充有标记样本集,并更新分类器。这两个过程不断迭代,直至算法收敛。
自训练方法不需要任何特定的假设,简单有效,已经被广泛应用在文本分类[5]、人脸识别[6]、生物医学[7]等多个领域。但是自训练分类算法也存在一些缺陷,比如分类性能受限制于初始标记数据集的大小以及它们在整个数据集上的分布,对标记错误样本的识别改进等。针对自训练方法的缺点,Gan 等人[8]考虑到数据集的空间分布,提出用半监督模糊c 均值聚类方法来优化自训练算法(ST-FCM)。该方法把半监督聚类技术作为一个辅助策略融合到自训练过程,半监督聚类技术能有效地挖掘到无标记样本含有的内部数据空间结构信息,更好地训练分类器。但模糊c 均值聚类方法不能很好地发现非高斯分布的数据集的空间结构。针对这一问题,Wu 等人[9]提出了基于密度峰值的自训练方法(Self-Training based on Density Peak of data,ST-DP)在ST-DP算法中,数据空间结构是用密度峰值聚类[10]的方法发现的。基于密度峰值聚类的方法虽然可以有效利用各种数据分布的空间结构,但是对一些可视化后有较多重叠样本的数据集,ST-DP的分类效果不好。随后,Wu等人用差分进化(Differential Evolution,DE)方法来改进自训练算法,提出了基于差分进化的自训练算法(ST-DE)[11]。该方法利用DE算法来优化自训练过程中新添加的有标记样本[12]。虽然ST-DE算法解决了样本重叠的问题,但是优化算法在一定程度上带来了过多的复杂运算,该方法没有从根本上解决ST-DP 算法的缺陷。主要原因是在自训练标记过程中,那些可视化后重叠的样本极其容易被标记错误。而ST-DP 算法将这些错误标记样本直接用于后续迭代标记,最终使训练的分类器性能下降。
在ST-DP 算法[9]的基础上,本文提出了一个基于密度峰值和切边权值的自训练方法(Self-Training method based on Density Peak and Cut Edge Weight,ST-DPCEW)。该方法不仅在选择未标记样本时,利用基于密度聚类的方法发现数据集的潜在空间结构,选出具有代表性的样本进行标签预测。更重要的是利用切边权值统计方法识别预测的标签是否正确,并进行修正或重新预测。切边权值和密度峰值聚类一起充分利用样本空间结构和无标记样本信息,解决了部分样本被标记错误的问题,减少迭代过程中的错误累积,能有效提高分类器性能。
1 本文算法
本文从自训练过程中被错误标记的样本入手来提高自训练半监督分类算法的分类准确率。在ST-DP 基础上,提出了ST-DP-CEW算法。首先,用密度聚类方法发现数据集的空间结构,可以在每次迭代过程中优先选择有代表性样本进行标签预测。然后,用切边权值统计方法判断样本是否被标记正确,用标记正确的样本更新有标记集合。上述过程一直迭代,直到所有无标记样本标记完全。
1.1 密度聚类发现数据空间结构
聚类是一种典型的无监督学习方法,聚类的过程可以发现数据空间结构。基于密度聚类的方法[10]可以发现非高斯分布的数据集的空间结构,并且可以自动确定簇的个数。
本文中设L={(xi,yi)}是有标记样本集,其中xi是训练样本,yi是它的标签,yi∈{ω1,ω2,…,ωs} ,i=1,2,…,m ,s 是类别数。U={xm+1,xm+2,…,xn}是无标记样本集。则样本xi的局部密度定义如下:

其中:

dij为样本xi和样本xj的欧式距离,dc被称为截断距离,它是一个没有固定值,与数据集本身有关的常数[9,13]。显然,样本的ρi值等于到xi距离小于dc的样本个数。
计算每个样本xi的ρi值后,找到距离样本xi最近且有更大局部密度的样本xj,将xi指向xj,即可找到数据集的空间结构。把被指向的样本xj称为“下一个”样本,样本xi称为被指向样本xj的“上一个”样本。
1.2 切边权值统计方法
切边权值统计[14]是一个识别和处理错误标记样本的方法。首先,为了说明样本的相似性,在数据集上建立一个相对邻接图。两个样本xi和xj有边相连,若满足如下条件:

其中,d(xi,xj)表示样本xi和xj之间的距离。在邻接图中,如果有边相连的两个样本的标签不同,则这条边被称为切边。
直观上,对于给定的样本xi,在它邻域内的所有样本应该属于同一类。因此,如果xi有很多的切边,即xi邻域内大部分样本的标签与xi的标签不同,则认为它可能被标记错误。因此,切边在识别错误标记样本中起着重要的作用。对于不同的样本,它们可能有相同切边的数量,但是每条切边的重要性不同,因此为邻接图中的每条边赋予权值。设wij为连接样本xi和xj的边的权值。
最后用假设检验的方法识别样本xi是否被标记错误。样本xi的切边权值之和Ji定义如下:

其中:

这里,ni为与样本xi有边相连的样本个数,yi是样本xi的标签。如果待检验样本xi的Ji值很大,认为该样本有可能标记错误。为了进行假设检验,要定义原假设如下:
H0,邻接图中的所有样本根据相同的概率分布proy彼此相互独立地被标记。这里proy表示样本标签为y 的概率。
在原假设H0下,样本xi邻域内所有样本的标签不是yi的概率不超过1-proyi。如果xi的Ji值明显低于H0下期望,则标记正确。否则样本可能标记错误。为了做双边检验,必须首先分析Ji在H0下的分布。在原假设下,Ii(j)是服从布尔参数为1-proyi的独立同分布随机变量。从而Ji在H0下的期望μ0和方差σ2分别为:

Ji在原假设H0下服从正态分布Ji~N(μ0,σ2),故选用的检验统计量为:

则有u~N(0,1),给定显著性水平α,可得出拒绝域为:

从而得到切边权值之和Ji的拒绝域为:

对于待测样本xi,如果其Ji值明显低于在H0下的期望,即在左侧拒绝域,则该样本标记正确,否则有可能标记错误。用切边权值统计方法识别错误标记样本的算法主要步骤如下:
步骤1 对样本集S 建立一个相对邻接图,并初始化正确标记样本集T={∅}和错误标记样本集T′={∅}。
步骤2 为邻接图中每条边赋予权值,计算每个样本xi的切边权值和Ji、原假设H0下Ji的期望μi和方差δi2。
步骤3 给定显著性水平α,计算xi的拒绝域。
步骤4 如果Ji值在左侧的拒绝域,则标记正确,更新正确标记集合T ←T ⋃xi;如果不在左侧的拒绝域,看它的近邻样本,若近邻样本全在T 内则用大多数标签标记重新标记xi,更新T ←T ⋃xi。否则xi标记错误,更新错误标记集合T′←T′⋃xi。
步骤5 重复上述步骤,直到所有样本检验完,将数据集S 划分为T、T′。
1.3 权值的选择
每条边的权值在切边权值统计方法中具有很重要的作用。本文中,权值是先利用每个样本的最大近邻距离来标准化邻域内的其他近邻距离[15]。再计算样本与每个近邻样本标签相同的概率,即为边的权值。
设样本集{xi,1,xi,2,…,xi,k}是样本(xi,yi)的k 个邻接样本,即它们与xi有边相连。xi为训练样本,yi是xi的标签,各个邻接样本与xi的距离满足条件d(xi,1,xi)≤d(xi,2,xi)≤…≤d(xi,k,xi)。用xi的第k 个近邻样本距离来标准化前k-1 个邻接样本到xi的距离,则标准化后的距离为:

然后将标准化距离转化为xi和样本xi,j有相同标签的概率P(xi,j|xi),即为邻接图中每条边的权值wij。

1.4 基于密度和切边权值的自训练算法
由于自训练算法在每步迭代时容易将无标记的样本标记错误,这些错误会参与到下一步迭代中,从而影响分类器的训练,降低算法性能。因此,在自训练过程中,识别标记错误样本对算法性能起着重要的作用。识别样本标签的方法有很多,常见的是基于分类器的过滤方法和基于最近邻规则的数据剪辑技术[14]。
基于分类器的过滤方法主要是在每次迭代训练时先把现有的有标记样本集平分成n 个子集,用相同的学习算法如C4.5在所有可能的n-1 个子集中训练得到n个不同的分类器。然后用n 个分类器对无标记样本进行分类,根据一致或多数投票原则选择样本的标签。基于最近邻规则的数据剪辑技术 主要依赖距离,根据k个近邻样本的标签来判断待预测样本标签是否正确。对于待预测样本xi,如果xi的标签和其k 个最近邻样本的所有或大多数标签不一致,则xi标记错误。
基于分类器的方法对样本集的划分和学习算法的选取要求极高。基于最近邻的方法对距离度量和k 值的选取都需要提前设定。如果提前选取不当会造成判断错误,影响最终的分类效果。而且这两种方法在识别过程中都没有利用到无标记样本所携带的大量有价值的信息,使得识别的准确率降低。
切边权值统计识别错误标记样本的方法不需要预先设定任何参数,也能够充分利用无标记样本的信息。因此,为提高自训练算法的分类准确率,本文将切边权值统计识别错误标记样本的方法融合到ST-DP算法中,提出了ST-DP-CEW算法。该算法先通过密度聚类方法发现数据集的空间结构,利用空间结果信息在迭代过程中优先选取有代表性的无标记样本进行标签预测,提高了预测标签的准确性。然后用切边权值统计的方法判断预测标签是否正确。将标记正确的样本用于下一次训练。算法的具体步骤描述如下:
步骤1 用密度聚类方法找到整个数据集的真空间结构,同时找到了每个样本xi的“下一个”和“上一个”样本。
步骤2(1)用KNN 或SVM 作为基分类器,用初始有标记样本集L 训练一个初始分类器;
(2)对L 中所有样本的“下一个”无标记样本进行标签预测;
(3)用切边权值统计方法识别“下一个”样本是否标记正确,得到正确标记的样本,更新L 和U ,接着更新分类器;
(4)重复(1)到(3),直到L 的所有“下一个”样本标记完。
步骤3(1)对已更新的L 中所有样本的“上一个”无标记样本进行标签预测;
(2)用切边权值统计方法识别“上一个”样本是否标记正确,得到正确标记的样本,更新L 和U ,接着更新分类器;
(3)重复(1)和(2),直到L 的所有“上一个”样本标记完。
显然,步骤3 和步骤2 类似,只是把步骤2 中的“下一个”换成“上一个”。ST-DP-CEW算法的伪代码如下:
输入:有标签样本集L,无标签样本集U 。
输出:分类器C。
1.for L ⋃U 中每个样本xido
2.利用公式(1)计算ρi
3.end for
4.找到所有样本的“下一个”和“上一个”样本;
5.用L 训练分类器C;
6.令L′为U 中有L 的所有“下一个”样本集;
7.while L′≠∅ do
8.用C 对L′中样本分类;
9.S=L ⋃L′,T=L,T′=∅;
10.在S 中根据公式(2)建立相对邻接图;
11.for L′中的每个样本xido
12.根据公式(3)、(4)、(5)计算切边权值和Ji以及原假设H0下Ji的期望μi和方差δi2;
13.给定显著性水平α,根据公式(6)、(7)、(8)计算拒绝域W ;
14.if Ji值在左侧拒绝域then
15.T ←T ⋃xi
16.else if xi邻域内所有样本在T 中then
17.重新标记xi,T ←T ⋃xi
18.else
19.T′←T′⋃xi
20.end for
21.更新L 和U ,L ←L ⋃T ,U ←UT ;
22.更新分类器C;
23.end while
24.令L′为U 中有L 的所有“上一个”样本集;
25.while L′≠∅ do
26.用C 对L′中样本分类;
27.S=L ⋃L′,T=L,T′=∅;
28.for L′中的每个样本xido
29.根据公式(3)、(4)、(5)计算切边权值和Ji以及原假设H0下Ji的期望μi和方差δi2;
30.给定显著性水平α,根据公式(6)、(7)、(8)计算拒绝域W ;
31.if Ji值在左侧拒绝域then
32.T ←T ⋃xi
33.else if xi邻域内所有样本在T 中then
34.重新标记xi,T ←T ⋃xi
35.else
36.T′←T′⋃xi
37.end for
38.更新L 和U ,L ←L ⋃T ,U ←UT ;
39.更新分类器C;
40.end while
41.return 分类器C
2 实验结果及分析
为了说明算法的有效性,将提出的算法与已有的自训练算法在8 个真实数据集上作了对比实验。数据集均来源于KEEL 数据库[16],相关信息如表1 所示。对Cleveland 和Dermatology 数据集删除有缺失值的样本,其余数据集不做任何处理。

表1 实验数据集
采用的对比算法有:以KNN、SVM做分类器的传统自训练算法、基于模糊c 均值聚类的自训练分类算法(ST-FCM)[8]、基于密度峰值的自训练分类算法(ST-DP)[9]和基于差分进化的自训练分类算法(ST-DE)[11]。具体参数设置如表2所示。

表2 实验中相关算法的参数设置
2.1 实验的实施
采用十折交叉验证的策略,利用KNN和SVM作为基分类器对数据集进行实验。把其中的一折作为测试集TS,其余九折作为训练集TR。每次实验都随机选取训练集中10%的样本作为初始有标记样本集L,其余的为无标记集U 。因此,数据集被划分为有标记集L、无标记集U 和测试集TS。其中L 和U 共同组成训练集TR。为了确保实验的准确性,重复做十次十折交叉验证实验,最后选取十次实验平均值作为最后实验结果。选用分类准确率(Accuracy Rate,AR)、平均准确率(Mean Accuracy Rate,MAR)和标准差(SD-AR)作为算法的分类性能的比较标准。计算公式如下:

其中:

这里,f(xi)是样本xi的预测标签,NTS是测试集的大小,n 是实验重复次数,MAR 代表算法的分类性能,SD-AR 代表算法的鲁棒性。选用MAR±SD-AR作为判断算法性能好坏的依据。
表3和表4分别给出了数据集以KNN和SVM作为基分类器的实验结果,其中加粗的数据说明在该算法上分类效果比较好。如表3 和表4 所示,当初始标记样本为10%时,在多数据集上ST-DP-CEW 的平均分类准确率明显优于其他对比算法。但是在算法以SVM为基分类器时,ST-DP-CEW 在数据集Cleveland 上的分类准确率基本没有提高,这主要是由于数据集中大部分属性的数值接近于0,对同一属性而言,各样本差异性较小,导致整体上样本间差异性小,各类别可区分性降低,影响最终的分类效果。
2.2 有标记样本比例的影响
另外,分析了初始标记样本比例对算法分类性能的影响,图1 和图2 分别给出了基分类器为KNN 和SVM时,几个算法的平均均分类准确率在初始标记样本比例为10%、15%、20%、25%、30%、35%、40%、45%以及50%时的变化趋势。
从图1 和图2 可以看出,在8 个数据集上无论是以KNN为基分类器还是以SVM为基分类器,本文提出的算法整体上优于其他对比算法。若以KNN作为基分类器,在8个真实数据集上本文算法在有标记样本比例极少的情况下平均分类准确率明显高于其他对比算法。若以SVM 作为基分类器,在Bupa、Dermatology、Glass、Ionosphere、pima、yeast 这6 个数据集上,本文的算法在有标记样本比例极少的情况下平均分类准确率明显高于其他对比算法。这是因为ST-DP-CEW在逐步添加无标记样本时,用切边权值统计的方法判断样本是否被标记正确,并进行修正或重标记。减少了迭代过程中的样本标记错误带来的负影响,从而提高了分类准确率。观察图1 和图2 还可以发现,随着初始标记样本比例逐渐增加,ST-DP-CEW 的平均分类准确率与其他对比算法整体上逐渐接近。这是因为有标记样本数量比较充足时,这些算法的平均分类准确率都相对比较稳定。提出的算法是基于有标记样本极其少的情况下提出的,主要应用于半监督分类,更适合在有标记样本比例较低的环境中进行分类。

表3 基分类器为KNN时的实验结果(MAR±SD-AR) %

表4 基分类器为SVM时的实验结果(MAR±SD-AR) %

图1 基分类器为KNN时算法的MAR值与初始标记样本比例的关系
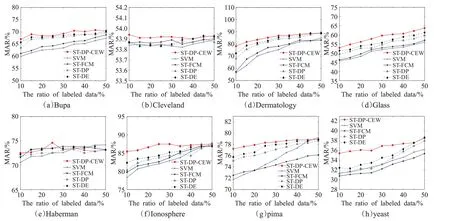
图2 基分类器为SVM时算法的MAR值与初始标记样本比例的关系
3 结束语
本文从自训练迭代过程中有可能被错误标记样本出发,在ST-DP算法基础上提出了基于密度峰值和切边权值的自训练算法。即将切边权值统计识别错误标记样本的方法融合到ST-DP 算法中。既考虑了数据集的空间结构,又解决了样本被错误标记的问题。另外,对邻接图中权值的计算也更好地利用数据集的空间结构以及无标记样本所携带的信息。在真实数据集上充分分析了ST-DP-CEW算法的有效性。特别是在初始有标记样本比例较低的情况下提出的算法较之已有算法,性能上有很大的提升。在后续工作中,将讨论如何更好地构建邻接图,并在识别过程中引入度量标签错误可能性大小的函数,使标签识别更精确。
