基于Gram-Schmidt变换的主基底分析两阶段变量筛选方法

郭 兵 ，胡伟芳，余江琼

(1. 湖南城市学院 理学院，湖南 益阳 413000；2. 吉首大学 数学与统计学院，湖南 吉首 416000)

在对数据进行综合评价的过程中，常常会涉及大量的初始数据变量.然而，这些数据变量之间可能存在一定的相关性，这会影响到主成分的提取及相应的评价效果，因而需要对初始数据变量进行筛选，即从中选取部分初始变量来进行分析.王惠文等[1]基于Gram-Schmidt 变换提出了基于主基底分析的变量筛选方法，并将筛选出来的变量集合进行分析.郭丽娟等[2]将主基底分析方法应用到具有二级指标体系的变量筛选中，并对区域创新能力进行评价.为了防止在变量筛选过程中一些重要变量被遗漏掉，仪彬等[3]提出了基于主基底分析的两阶段变量筛选方法.通过Gram-Schmidt 变换，Liu 等[4]将泛函变量选取应用于多元泛函线性回归.袁炜楠等[5]将主基底分析方法用于水稻冠层叶片叶绿素含量的估算.

本研究对基于主基底分析的两阶段变量筛选方法进行了改进，并在此基础上进行主成分分析，最后结合实际案例进行综合评价，探寻该方法的评价效果.

1 主基底分析的变量筛选方法

给定1 组数据变量，通过Gram-Schmidt 变换来构造该数据变量空间的1 组正交基底，将正交基底中的每个变量称为G-S 变量.在构造G-S 变量过程中，每个G-S 变量均与初始变量中某个变量存在着对应关系，此时与正交基底相对应的初始变量集合就被称为筛选变量集.本文将介绍该变量筛选方法的相关定义及变量筛选准则[1,6].

1.1 主基底定义

1.2 基于最大方差法的主基底分析变量筛选步骤

2 改进主基底分析变量筛选方法

最后，考虑最小值问题

不妨有

3 案例分析

通过基于最大方差法的主基底分析变量筛选法和改进的主基底分析变量筛选法，对具有二级指标体系的变量进行两阶段变量筛选.首先，从每个一级指标中选取部分重要的二级指标；其次，将筛选出来的这些二级指标组成1 个新的指标集合，并进行第2 次变量筛选；最后，在此基础上进行主成分分析，给出相应的综合评价.

3.1 样本数据

仪彬等[3]基于主基底变量筛选和主成分分析，对我国 2010 年区域创新能力进行了评价.本研究将对《中国区域创新监测数据2013》[7]进行分析，从中获取2012 年全国各省、自治区(不包括港、澳、台)、直辖市反映创新活动特征的数据，包含5 个一级指标和52 个二级指标 x1, x2, …,x52，具体内容如表1 所示.

3.2 基于主基底分析的变量筛选方法

首先，基于最大方差法对每个一级指标中的二级指标变量选取其最大线性无关组；其次，基于改进的主基底变量筛选方法，选取每个一级指标中合适的初始变量.

3.2.1 基于最大方差法选取最大线性无关组

按照1.2 节中的步骤1)～7)，对每个一级指标中的二级指标变量集合选取1 个极大线性无关组，并按照其方差的大小排序，如表2 所示.

3.2.2 基于改进的主基底变量筛选

通过改进的主基底变量筛选方法，对每个一级指标的极大线性无关组进行重新排序，所得结果如表3 所示.

首先，基于最大方差法的主基底变量筛选从表2 的每个一级指标中选取前2 个初始变量，来构成新的变量集合

其次，基于改进的主基底变量筛选从表3 的每个一级指标中选取前2 个初始变量，来构成新的变量集合{x5, x2, x8, x9, x20, x27, x30, x36, x43,x51}；

表1 区域创新能力监测指标体系

表2 基于最大方差法的主基底变量筛选

表3 改进的主基底变量筛选

3.3 基于主成分分析的综合评价

1)通过筛选所得到的 8 个初始变量为{x8, x29, x19, x13, x47, x2, x43,x5}，计算出其相关矩阵和前4 个主成分对应的特征值与贡献率，具体结果如表4 所示.

显然，基于前4 主成分的累积贡献率已达到82.378 8%.因此，继续以这4 个主成分的贡献率为权重，构建主成分分析评价模型，所得31 个地区的综合评价得分及排名如表5 所示.

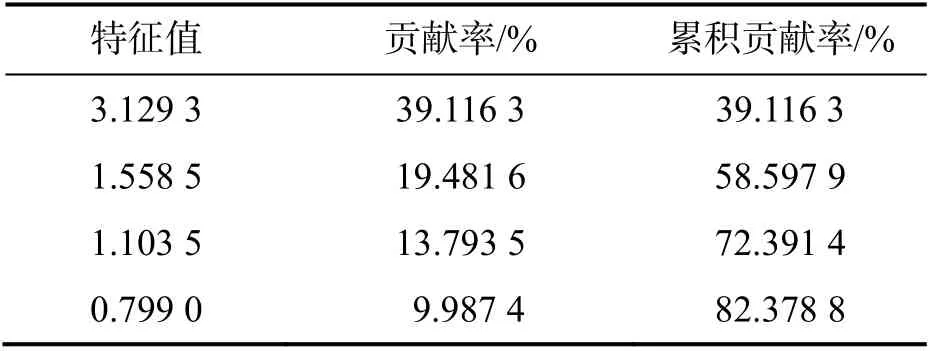
表4 前4 个主成分的特征值与贡献率

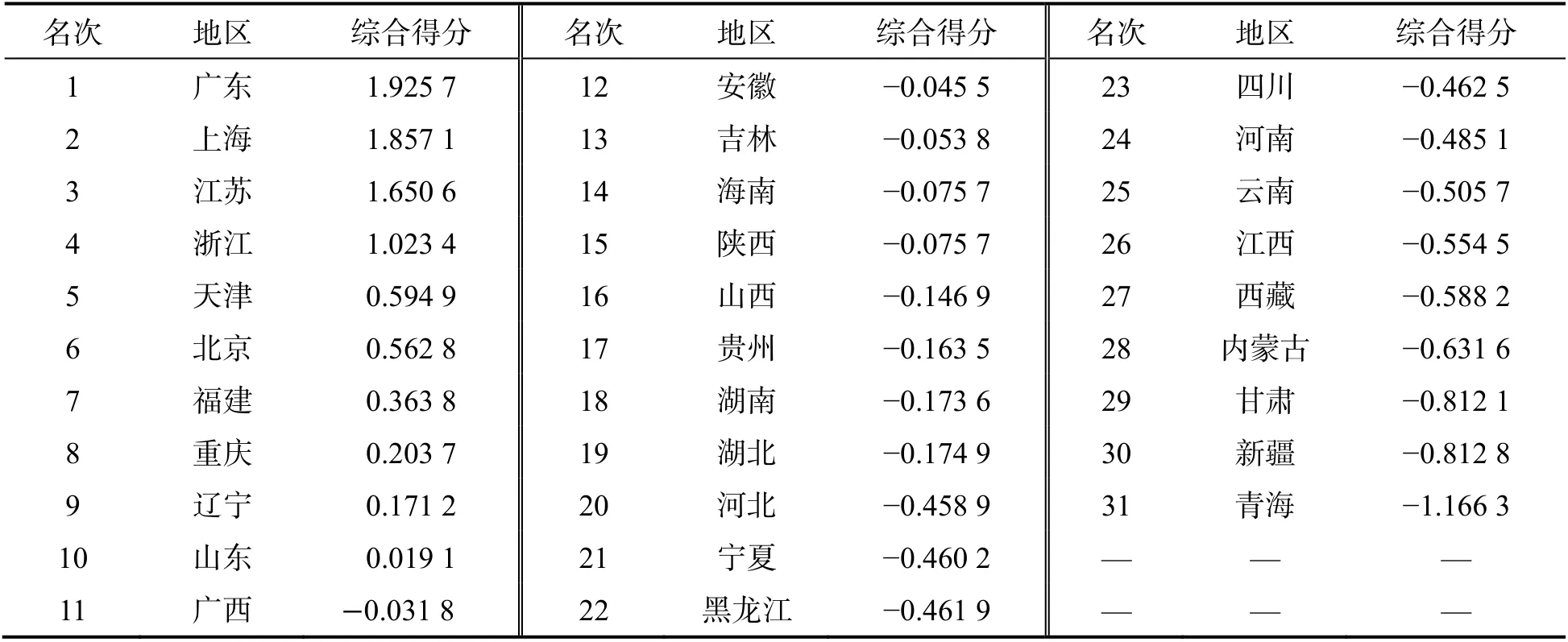
表5 31 个地区(不含港澳台)的综合得分

由表5 可知，广东、上海、江苏、浙江、天津、北京、福建和重庆位列前8 位，北京只排在第6 位，广西、贵州、海南和山西的排名在湖南、湖北和四川的前面，这和实际情况不太符合.

2)通过筛选所得到的 8 个初始变量为x8, x43, x9, x51, x5, x2, x20,x36，计算其相关矩阵和前4个主成分对应的特征值与贡献率，如表6 所示.

表6 中，基于前4 主成分的累积贡献率已达到88.804 3%，因此以这4 个主成分的贡献率为权重，构建主成分分析评价模型，得到这31 个地区的综合评价得分及排名，如表7 所示.

由表7 可知，在区域创新能力方面，上海、广东、北京、天津、江苏、浙江、福建和山东位列前8 名，明显优于其他地区；山西和宁夏表现比较突出；作为人口大省的河南，在该模型的评价中，排名比较靠后.对比表5 和表7 发现，表7 的综合得分排名更为合理.

表6 前4 个主成分的特征值与贡献率

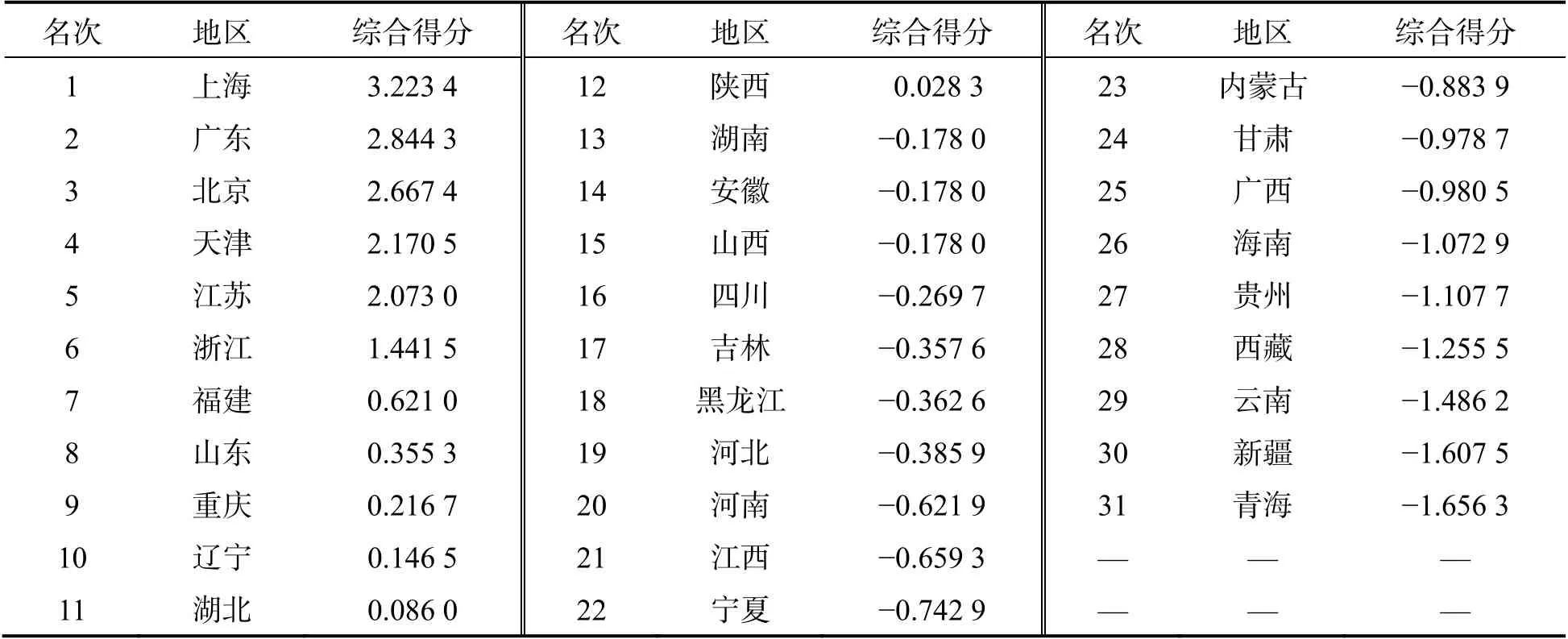
表7 31 个地区(不含港澳台)的综合得分

4 结论

利用主成分分析法对大量数据进行综合评价时，为了降低数据变量间的冗余信息量，需要对初始变量进行筛选.基于 Gram-Schmidt 变换的主基底分析两阶段变量筛选方法，能够有效地对多级指标体系的初始变量进行筛选；对全国 31个地区(不包括港澳台)的2012 年创新监测数据进行综合评价，得到了一个合理的综合得分排名.