合成旅工程保障能力多层次灰色系统评价方法*
2021-01-22范纪松
范纪松,任 辉,高 俊
(1.陆军工程大学训练基地,江苏 徐州 221004;2.空军勤务学院,江苏 徐州 221000)
0 引言
工程保障是保障己方部队隐蔽安全、指挥稳定和战场机动等,阻止和迟滞敌方部队机动的重要军事行动。战场工程保障本身具有点多、线长、面广的特点,对其能力进行建模和综合评价一直以来都是一个难题。另外,合成旅作为军改之后重建的单位,其工程保障力量结构与属性有所调整。因此,对合成旅工程保障能力进行建模和评估具有较强的现实意义,是一项比较复杂的系统工程。
综合评价方法是一个多学科、边缘交叉的新兴研究领域,主要从统计学、系统工程学或具体专业角度对社会、经济、军事等问题进行研究分析,目前综合评价方法运用比较广泛的有层次分析、模糊综合评判、数据包络分析、人工神经网络、灰色系统等方法。运用现代综合评价方法对工程保障能力模型进行评估,这方面的研究资料主要有:文献[1]将信息化条件下工程保障能力生成模式进行了全面、系统分析,并利用“云”理论评价模型,对工程保障能力要素属性进行分析评价;文献[2]将直觉模糊综合评价方法用于工程保障能力评估;文献[3-4]在对比多种能力分析方法的基础上,提出了采用定量仿真模型分析战时工程保障能力的方法。本文运用灰色理论对合成旅工程保障能力进行评估分析,提出的方法适用性强、操作简单,便于对多个单位工程保障能力进行分析比较评判。
1 工程保障能力评价体系的设计
结合合成旅工程保障任务,按照工程保障的专业功能来划分,可以分为工程侦察能力、构筑指挥所能力、工程伪装能力、机动保障能力、障碍设置能力、破障能力、构筑给水站能力等7 个要素,以及28个三级指标,如图1 所示。
2 多层次灰色系统评价模型
在控制论中,人们常用颜色的深浅来形容信息的明确程度。用“黑”表示信息未知,用“白”表示信息完全明确,用“灰”表示部分信息明确。灰色系统是介于信息完全知道的白色系统和一无所知的黑色系统之间的中间系统。灰色系统是贫信息的系统,一般统计方法难以奏效。灰色系统理论能处理贫信息系统,适用于只有少量观测数据的项目。灰色系统理论是我国著名学者邓聚龙教授于1982 年提出的。他的研究对象是“部分信息已知,部分信息未知”的“贫信息”不确定性系统,通过对部分已知信息的生成、开发实现对现实世界的确切描述和认识。灰色系统理论主要是利用已知信息来确定系统的未知信息,使系统由“灰”变“白”。其最大的特点是对样本量没有严格的要求,不要求服从任何分布。

图1 合成旅工程保障能力模型指标体系
关联分析是灰色分析、评价和决策的基础。灰色关联分析(Grey Relational Analysis)提供了一种定量分析两因素集之间相互关联程度的方法。这里采用灰色关联分析评价工程保障能力的基本思路是:以理想合成旅工程保障能力各指标值作为参考数列X0的各实体x0k,被评价旅的各指标作为比较数列Xi的各实体xik,求关联度ri。关联度越大,说明被评价旅指标与理想状态越相似,其工程保障能力越强;反之,则保障能力越弱。因此,关联度的大小顺序,就是被评价旅工程保障能力强弱的次序。其评价步骤[5-6]如下:
Step 1 选择参考数列
设:i 为第i 个评价单位的序号,i=1,2,…,m;k为第k 个评价指标的序号,k=1,2,…,n;vik为第i 个评价单位的第k 个指标的评价值。取每个指标的最佳值的v0k参考数列V0的实体,于是有:
V0=(v01,v02,…,v0n)
式中,v0k=Optimum(vik),i=1,2,…,m,k=1,2,…,n。
对一个由m 个评价单位,n 个评价指标的系统,有下列矩阵:
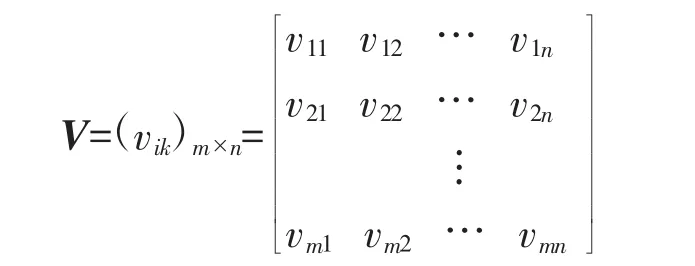
选取的参考数列为:
V0=(v01,v02,…,v0n)
Step 2 指标值规范化处理
为了使各指标之间可以比较,需要对各指标值进行规范化处理,处理的目标是为了使数值无量纲化,处理方法一般有以下3 种:
1)初值化
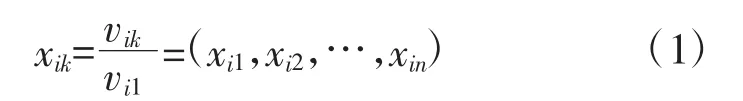
初值化方法适用于有一定趋势现象的无量纲化,比如,呈稳定增长(下降)趋势的数列,通过初值化处理,可使增长(下降)趋势更加明显。
2)均值化
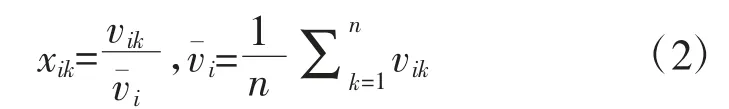
一般说来,均值化方法比较适合于没有明显升降趋势现象的数据处理。
3)区间化

3 种方法不宜混合、重叠作用,在进行系统因素分析时,可根据实际情况选用其中一个。
进行规范化处理之后,得:

Step 3 计算关联系数
把规范化后的数列X0=(x01,x02,…,x0n)作为参考数列,Xi=(xi1,xi2,…,xin)(i=1,2,…,m)作为比较数列,关联系数的计算公式为:

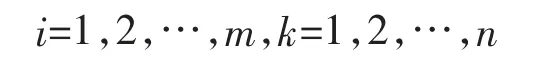
式中,ρ 是分辨系数,ρ∈[0,1]。
利用公式计算关联系数ξik,得到下列关联系数矩阵:

式中,ξik为第i 个评价单位第k 个指标与第k 个最佳指标的关联系数。
Step 4 计算单层次的关联度
考虑到各指标的重要程度不一样,所以关联度计算方法采取权重乘以关联系数。根据专家法得到某一层的各指标相对于上层目标的优先权重为:

Step 5 计算多层评价系统的最终关联度
对一个由L 层组成的多层评价系统,最终关联度的计算方法如下:将第k 层各指标的关联系数进行合成,分别得到它们所属的上一层即k-1 层各指标的关联度;然后把这一层所得到的关联度作为原始数据,继续合成得到第k-2 个指标的关联度,以此类推,直到求出最高层指标的关联度为止。
Step 6 工程保障能力大小排序
依据关联度ri(i=1,2,…,m)大小进行排序,关联度的大小顺序即为工程保障能力优劣次序。
3 实例分析
如前文所述合成旅工程保障能力指标体系(图1),该体系由3 层指标组成,第1 层:目标层,工程保障能力(B);第2 层:要素层,包括工程侦察能力(B1)、构筑指挥所能力(B2)、工程伪装能力(B3)、机动保障能力(B4)、破障能力(B5)、障碍设置能力(B6)、构筑给水站能力(B7);第3 层:指标层,共28 个指标。
3.1 确定指标体系各层次权重及综合权重
利用专家调查法,以及层次分析(AHP)赋权,具体层次分析法的过程在这里省略,直接给出结果,各层次单层权重分别为:
工程保障能力,WB=(0.067 0,0.138 6,0.071 0,0.245 0,0.259 6,0.125 5,0.093 2)
工程侦察能力,WB1=(0.459 8,0.138 4,0.124 9,0.138 4,0.138 4)
构筑指挥所能力,WB2=(0.458 7,0.072 5,0.072 5,0.241 0,0.155 2)
工程伪装能力,WB3=(0.637 0,0.258 3,0.104 7)
机动保障能力,WB4=(0.139 2,0.371 4,0.269 2,0.139 2,0.081 0)
破障能力,WB5=(0.375 0,0.375 0,0.125 0,0.125 0)
障碍设置能力,WB6=(0.166 7,0.333 3,0.333 3,0.166 7)
构筑给水站能力,WB7=(0.500 0,0.500 0)
因此,底层指标综合权重如表1、图2 所示。从图2 中可以直观地看到,“工程侦察能力”中的指标权重相对较低,而“机动保障能力”和“破障能力”中的指标权重相对较高。
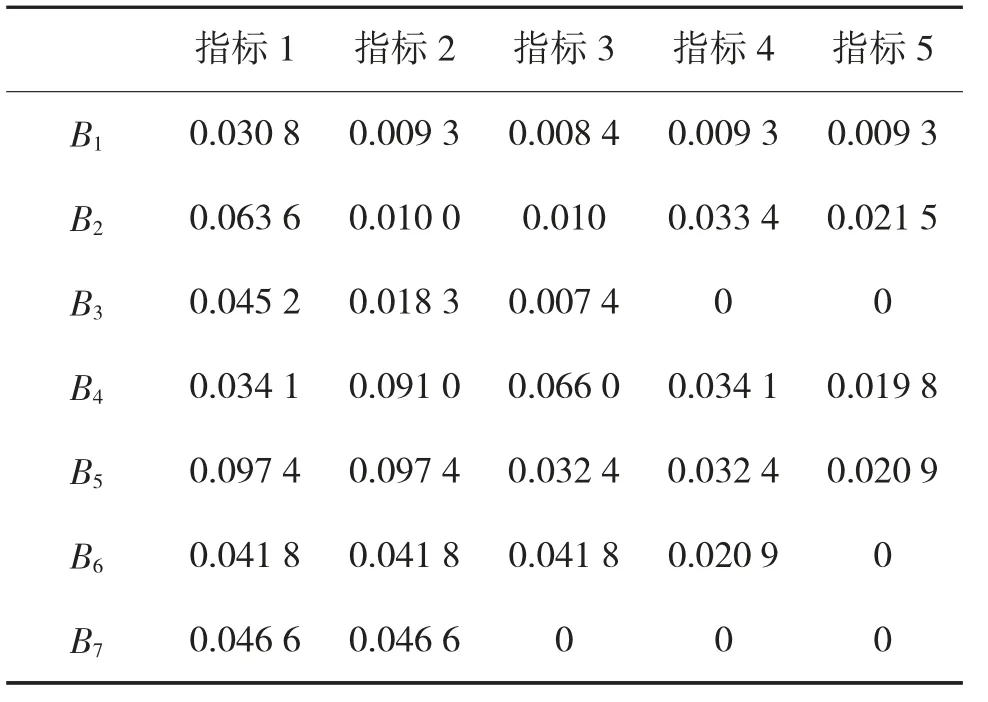
表1 综合权重表
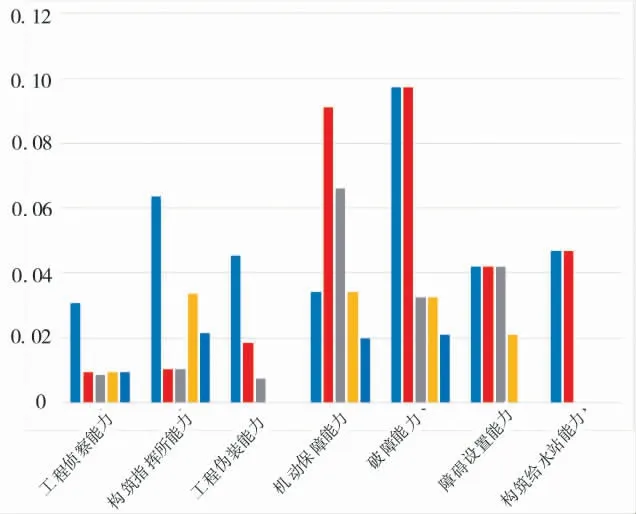
图2 综合权重分布图
3.2 确定评价指标的值
工程保障能力模型的指标取值类型比较复杂。在三级指标中,对于能够比较方便定量化处理的指标,例如,“侦察数据获取”“工事构筑”、“道路作业”、“扫雷作业”等,选取其典型行动中作业能力或作业时间作为量化值,如表2[7]所示。如果系统指标Vi与主行为V0成负相关关系,比如作业时间,可采取逆化或倒数化,进行规范化处理。对于难以定量化处理的指标,例如,“警戒与保障”、“警戒掩护”等,采取结合专项演练考核评估打分的方式得到指标评分,如将指标划分为“优秀”、“良好”、“及格”、“不及格”四级制,[9,10]分为“优秀”,[7,9)分为“良好”,[6,7)分为“及格”,[0,6)分为“不及格”。
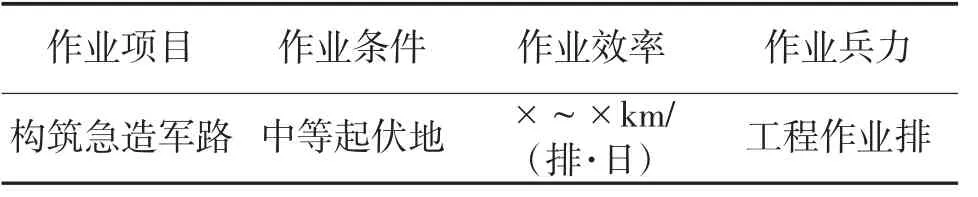
表2 道路作业能力
其具体评价指标值的过程省略。为便于后期统一衡量,指标值经规范化处理到0~10 之间。
以4 个合成旅的工程保障能力模拟数据(V1,V2,V3,V4)为例,如下页表3 所示,合成旅V1的特点是侦察、体能素质较高,因此,指标B11、B14、B71数值较高;合成旅V2的特点是工程作业能力较强,指标B21、B31、B42数值较高;合成旅V3的特点是各方面比较均衡,没有太突出的指标,也没有短板;合成旅V4的特点是相关保障能力较强,但作业能力偏弱,指标B25、B33、B45数值较高。参考数列取v0k=Optimum(vik),如表3 所示。
3.3 计算单层关联度
根据式(4),取分辨系数ρ=0.5,计算得各指标与参考数列的关系系数ξik(i=1,2,…,m;k=1,2,…,n),值列于表4 中。
3.4 多层结构关联度合成
利用式(5)R=WET可以得到第2 层指标的关联度矩阵:

进一步可求得最高层指标B 的关联度,用第1层权重矩阵WB乘以第2 层关联度矩阵RBx。
RB=WBRBx=(0.588,0.618,0.694,0.585)工程保障能力排序:按照RB中关联度大小得到合 成 旅 工 程 保 障 能 力V1、V2、V3、V4优 劣 次 序 为V3>V2>V1>V4。该结论显示,各方面都比较均衡的合成旅V3,优于工程作业能力较强的合成旅V2,优于侦察、体能素质较高的合成旅V1,优于保障能力强、作业能力弱的合成旅V4。
4 结论
本文针对合成旅工程保障能力生成特点,构建了工程保障能力指标体系,结合灰色理论与层次分析法(AHP)赋权,对工程保障能力进行了效能评价。能够为合成工程保障能力评估和考核提供支撑和依据,下一步还将进一步根据考核评估结论数据,完善工程保障能力体系与改进综合评价方法,以使评估结论更能符合实际情况。

表3 工程保障能力各指标模拟值与理想值
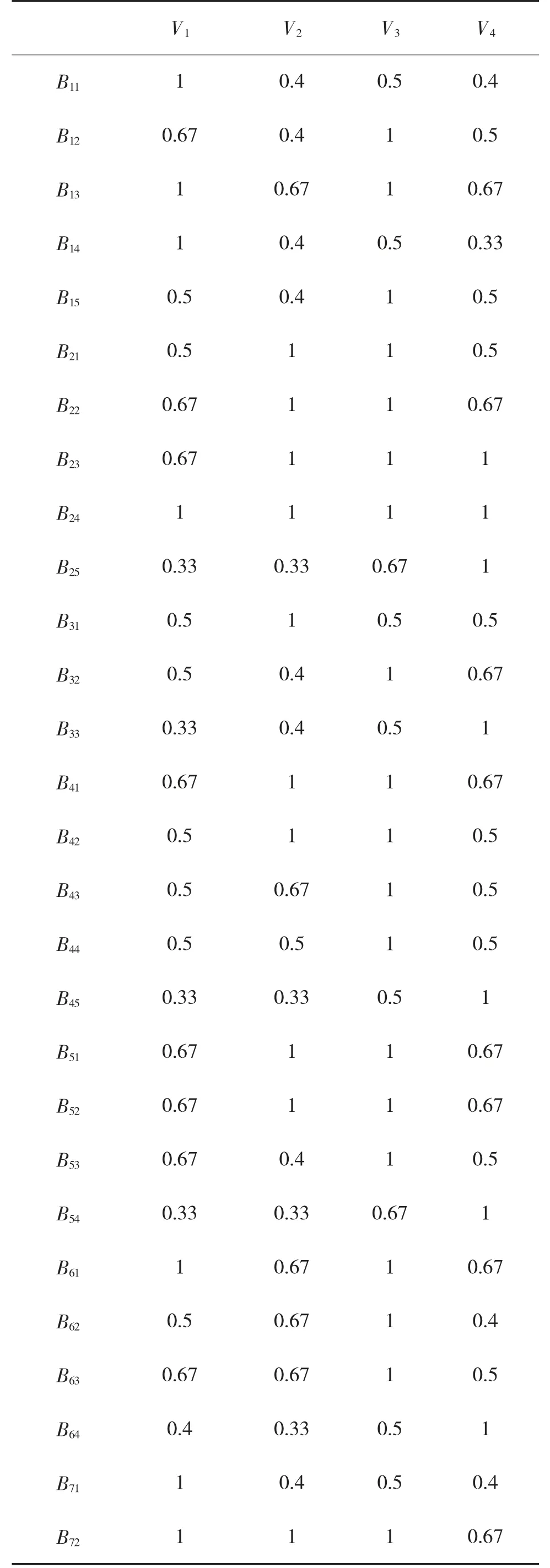
表4 各指标与参考数列关联系数(ξik)表
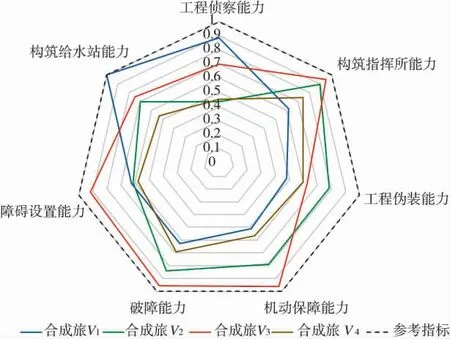
图3 第2 层指标关联度雷达图
