破障火箭弹终点毁伤效能评估研究

2021-01-22王树山梁振刚李元生

火力与指挥控制 2020年12期

高源，王树山，梁振刚，舒彬，李元生

（1.北京理工大学，北京 100081；2.沈阳理工大学，沈阳 110159；3.北京中恒天威防务科技有限公司，北京 100081；4.中国船舶工业系统研究院，北京 100094）

0 引言

轨条砦作为典型的反登陆障碍物，通常以集群形式布设在水际滩头，以起到阻碍和延缓敌方登陆的作用，因此，“破障”也就成为了登陆作战不可避免的难题［1］。随着信息化、智能化的弹药在破障武器上的应用，破障火箭弹已经成为执行破障任务的主要武器，火箭弹可以将战斗部投放到预定的破障区域，形成具有面杀伤能力的爆炸网络［2］。使破障行动可以用更小代价完成预期的作战任务。然而在基于计算机仿真的毁伤评估技术快速发展的今天，针对这类由障碍物组成的集群目标，破障火箭弹的终点毁伤效能评估手段和方法还不明确，需要在传统的毁伤效能评估方法上加以完善和发展。

针对武器（弹药）对集群目标的毁伤效能评估，姜广顺等［3］提出了以目标工作能力损伤情况作为目标毁伤评估的评判依据，通过构建总毁伤的广义分布函数作为目标处于无工作能力（无战斗力）状态的最短时间函数，以实现对集群目标的总毁伤的概率特性评估。刘彦等［4］和蒋海燕等［5］研究了导弹阵地类集群目标的毁伤效能评估方法，对于导弹阵地内的指挥控制车，雷达车等目标，构成“串联”式结构，只要其中一个目标被毁伤，则导弹阵地被毁伤，阵地内所有的发射车构成“并联”式结构，全部毁坏视为阵地丧失战斗功能。赵东华等［6］针对幅员较小的集群目标，提出了以阵地内子目标的毁伤概率为基础，取所有毁伤概率的平均值作为整个集群目标的毁伤概率。刘文举和魏琳［7］针对末敏弹对集群目标的毁伤，提出了以耗弹量、毁伤目标相对数和效费比作为效能指标的计算方法。沙兆军等［8］则是针对子母弹对集群目标打击，采用集群目标中正面和纵深所有子目标的毁伤概率之和来表征整体的毁伤概率。

对于由轨条砦组成的障碍物集群目标，具有两个主要特点：一是这类集群目标中的单元目标（子目标）数量较多，功能作用相同且相互独立；二是破障作战任务是开辟登陆通路［9］，毁伤一定的数量或比例即可达到战术指挥预期。基于以上特点，可见传统的对集群目标毁伤评估方法对此类效能评估问题适用性较差，缺乏合理的毁伤效能表征方法。本文在传统的毁伤效能评估方法基础上，研究和建立破障火箭弹终点毁伤效能评估方法及模型，以期为类似于滩头障碍物集群目标的毁伤效能评估提供参考，为破障武器的设计及战场指挥提供技术和数据支撑。

1 破障火箭弹终点毁伤效能表征方法

有了毁伤信息并不等于有了目标的毁伤结果和毁伤程度，还需要利用合适的评估模型方法对毁伤信息进行处理。建立评估模型方法可以说是实现了从简单的人工判断发展到定性定量分析的突破口［10］。针对不同的弹药，其终点毁伤效能表征方法也不尽相同，对于障碍物类集群目标，基于效费比和作战效率等因素，采用带有一定制导火箭武器是目前登陆破障最好的选择。针对不同的目标类型，才存在效能表征方法的差异性。对于独立的点目标，采用“单发毁伤概率”和“达到期望毁伤概率的用弹量”是目前主流的战斗部毁伤效能定量表征指标［11］。然而对于由多个子目标构成的集群目标，在计算了每个子目标的单发毁伤概率的基础上，需要一种合理可行的表征方法来评估整体的毁伤效能。然而对于不同种类的集群目标，基于集群目标整体和集群中子目标功能作用以及易损性的差异，其表征方法也不尽相同。对于登陆作战时所面对的障碍物集群目标，破障任务是对滩头障碍物目标集群的打击，通过毁坏一定数量或比例的障碍物目标以起到为登陆部队开辟通路的作用。因此，对于破障火箭弹的终点毁伤效能评估，需要在期望概率之前增加一个“毁伤目标数量或比例”的前提条件，即采用“达到毁伤一定比例或数量的期望概率所需用弹量”作为相应的效能评估指标。

从概率统计角度来讲，这里所指的概率，不同于传统毁伤评估中的毁伤概率，它表示“毁伤一定比例或数量”这一事件的发生概率。从工程上毁伤效能评估和实际作战指挥角度来讲，即完成预定作战期望的概率［12］。在数理统计中，“小概率事件”和假设检验的基本思想为“小概率事件”通常指发生的概率小于5%的事件，认为在一次试验中该事件是几乎不可能发生的。在工程计算中，需要在此基础上，依据实际作战任务的需求和重要程度，提出合理的期望概率。

在实际的工程计算中，毁伤目标比例或总数量不同则达到相同期望概率所需用弹量差别非常大，另一方面，造成相同比例或数量毁伤时，达到不同的期望概率所需用弹量也会存在较大的差异。而且在使用压制类武器对集群目标战术打击选择时，如果想要达到100%数量上的毁伤或接近于期望概率100%，所需用弹量一定会相对巨大，且难以实现。因此，在这种评估方法中，在已知集群目标中每个子目标的毁伤概率的基础上，既需要根据实际的战略决策期望来明确所需毁伤目标的比例或数量，还需要确定所期望概率，最终以用弹量来表征最终的毁伤效能。

2 破障火箭弹终点毁伤效能评估模型

2.1 目标模型及毁伤律

轨条砦作为反抢滩登陆的常用障碍物，放置于便于登陆的地段，阻碍敌方兵力登陆，常常成为交战时登陆作战敌我争夺的重要目标之一。由轨条砦组成的滩头反登陆区域如图1 所示。

1937年“卢沟桥事变”爆发，中华民族全面抗战开始，国共实现了第二次合作。此时的国民政府采取积极的抗日政策，将抗战与教育相结合，逐渐认识到儿童在抗战中的作用，深化了对战时小学教育重要性的认识。1937年8月11日国民政府行政院发布《总动员时督导教育工作办法纲领》，明确规定，学校“务必镇静，以就地维持课务为原则”，而在“比较安全区域内之学校，尽可能范围内，设法扩充容量，收容战区学生”［7］1。此时的国民政府意识到教育对于抗战的重要作用，强调即使在困难时期，也必须充分保障教育的正常实施。

图1 轨条砦组成的反登陆区域

轨条砦由混凝土基座和斜置钢轨构成，一般在便于登陆地段设置，通常为2 列至3 列，列距7 m，间距3.5 m。假设预开辟一个沿海岸线长度约30 m的登陆区域，构建由轨条砦构成的反登陆目标区域等效模型，轨条砦共3 列，每列布置10 个，由于轨条砦体积相对于整个目标区域来较小，故在对整体集群目标分析时，可将每个轨条砦目标视为质点，以简化计算。目标区域等效模型示意图如图2 所示。

对于破障火箭弹对单独轨条砦目标的毁伤，为了简化计算，可以根据轨条砦的目标易损性数据和毁伤元的威力参数，将破障火箭弹威力场简化为威力半径，轨条砦的毁伤概率为：

图2 目标区域障碍物排布示意图

式中，r 为目标于弹药炸点的距离（m），r*为破障火箭弹的威力半径（m）。

2.2 炸点分布计算模型

在毁伤效能评估中，为了能得到最为接近实际的毁伤概率，一般通过计算机仿真程序对弹药实际炸点进行较大样本数量的模拟。基于大数据统计可以认为，在“目标无对抗、系统无故障”的前提条件下，弹药的实际炸点符合正态分布规律。破障火箭弹的终点弹道落角范围在75°～85°之间，且多为触发引信，因此，在终点毁伤效能计算中，可以将落角简化为90°，火箭弹随机弹道的炸点与目标在同一平面。

蒙特卡洛抽样方法如下［13］：

用一对［0，1］区间的均匀随机数r1，r2按以下数学式构成一对标准正态分布随机数，即：

2.3 毁伤概率计算模型

武器系统对目标的毁伤效率可用全概率公式描述。在假设目标无对抗、系统无故障的条件下，根据全概率公式，单发战斗部对独立目标的毁伤概率为［15］：

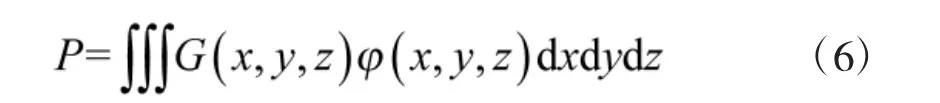
式中，G（x，y，z）为坐标杀伤规律，战斗部威力参数、目标易损性和战斗部与目标的相对位置所决定，φ（x，y，z）为炸点分布密度函数，由制导误差分布和引信启动规律确定。

蒙特卡洛方法对目标阵地的毁伤概率进行统计试验，根据瞄点的选择，抽取随机炸点的坐标给定样本容量s，在单一瞄点时，每次抽样一发，在多瞄点的打击方式下，多个瞄准点每次各抽样一发。累计各子样的蒙特卡洛统计数据，得到子样毁伤概率的期望估值［16-17］。每个独立障碍物目标的单发毁伤概率的蒙特卡洛估值为：

式中，Pai即为第i 个子样对第a 个障碍物目标的单发毁伤概率。

m 发弹药打击下，障碍物目标的毁伤概即为：

由一定数量的独立目标即组成一个集群目标，在目标破障区域内，每个独立的障碍物目标毁伤概率不同，引入概率统计的有关知识，即可求得毁伤一定比例或数量的概率。设每个独立的障碍物目标的毁伤概率分别为pk（k=1，2，3，…，n）

1）仅毁伤m 个障碍物目标的毁伤概率为

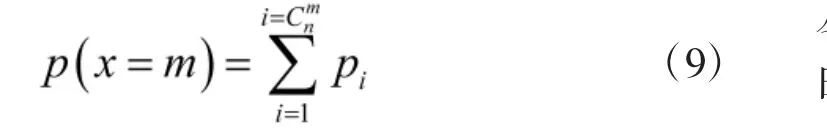
式中，pi为第i 种组合所求得的毁伤概率。

2）至少m 个轨条砦目标毁伤的概率为：

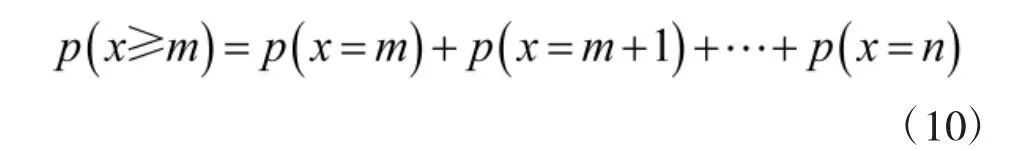
或应用对立事件来表示

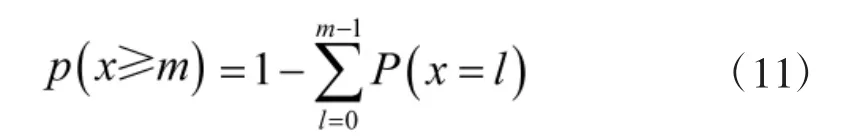
2.4 程序设计

基于以上数学模型，采用C#语言编制相应的破障火箭弹终点毁伤效能评估程序，程序流程图如图3 所示。

3 实例计算分析

基于以上方法和模型，以某破障火箭弹为例，威力场半径7 m，CEP=20 m，打击方案选择双瞄点打击，选取y 轴两侧面积相同的矩形的几何中心为瞄点，瞄点坐标分别为A1（-7.875，0），A2（7.875，0），如前文图2 中所示。针对所构建的以轨条砦组成的反登陆目标区域执行破障任务时的终点毁伤效能进行计算分析。

图3 程序流程图

分别计算了在达到相同概率时，毁伤不同比例轨条砦目标所需的用弹量以及在期望概率不同时，毁伤相同比例的轨条砦所需的用弹量，针对毁伤比例80%、90%和100%时用弹量-期望概率曲线，以及期望概率85%、90%和95%时用弹量-毁伤比例曲线进行了对比分析。

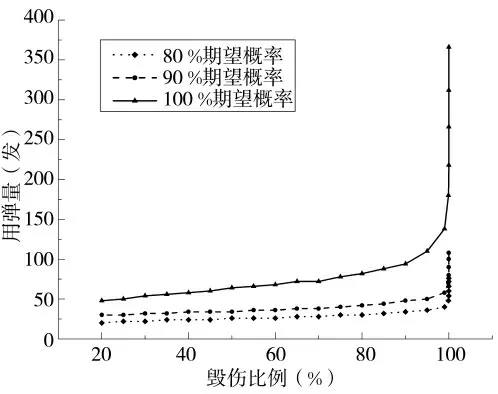
图4 用弹量与期望概率关系曲线

由图4 可以看出，在毁伤比例相同时，用弹量随着期望概率的增加而增大。在期望概率小于95%时，用弹量随期望概率的增加较为平缓，随着期望概率趋近于100%，所需用弹量急剧增大，根据曲线趋势，可以预测，当概率无限趋近100 %时，所需用弹量也趋于无穷。上述计算结果表明，无论是理论上数学概率统计计算，还是工程上的毁伤效能评估计算，概率上的无限趋近100%都是很难实现的。当期望概率趋近于100%时，用来衡量终点毁伤效能的指标-用弹量的大小就仅存在数学层面的意义，其结果对于工程上毁伤效能评估的价值意义很小。因此，在火箭弹对集群目标的终点毁伤效能评估中，应基于合理的数学概率理论以及预期作战任务的背景，提出合理的期望毁伤概率。

图5 用弹量与毁伤比例关系曲线

达到相同期望概率条件下，毁伤比例越高，所需的用弹量也会有明显增加，且在相同期望概率时，毁伤比例80%和毁伤比例90%两种条件下用弹量的相差不大，达到100%毁伤比例的用弹量明显高于前两者。

由图5 可以看出，在相同期望概率时，用弹量与毁伤比例成正相关，随着毁伤比例越大，所需用弹量越多，且增幅也不断增大。在达到100%毁伤比例时，所需用弹量远远大于毁伤80%时的用弹量；在相同毁伤比例时，期望概率越大，所需用弹量越大，所得规律与图1 所述相同。基于以上数据规律，可以看出，在打击由离散独立目标组成的集群目标时，全部毁伤（毁伤比例100 %）所需代价条件相对较大。对于破障任务来说，战术预期是开辟一定宽度的通路，所以，在破障火箭弹的终点毁伤效能评估中，对于战术预期的登陆区域内的轨条砦目标，选择80%～95%区间内的毁伤比例具有较高的工程参考价值。

综合来看，除了得到了评估模型中最基本的规律性认识，也可以通过数据规律看出，对于压制类武器打击集群目标时，达到数量上100%毁伤所需用弹量相对难以接受，在实战中资源消耗巨大，不具有可操作性。另一方面，基于Monte-Carlo 方法的毁伤评估模型决定了期望概率达到100%在数理上无法实现，在实际作战中，也无法做到100%战术行动的成功。计算结果符合理论预期，可以验证所建立的评估模型的合理性。