基于三阶蛇形机动模型的跟踪算法分析研究*

邱晓波，许乾坤，单东升

（1.陆军装甲兵学院兵器与控制系，北京 100072；2 解放军66133 部队，北京 100144）

0 引言

运动模型是地面装甲车辆火控系统解命中问题中的重要理论基础，随着未来信息化战争的不断发展，以及在未来战场上多样式的任务需求而迫切需要对其进一步深入研究［1］。当前，singer 模型［2］、Jerk 模型［3］、当前统计模型［4］、交互多模型及其改进模型［5-8］大都得到了迅猛发展和广泛应用，它们在单方向数据处理上有一定精度，但对于蛇形运动来说，其精度和适用性还存在不足。文献［9］中以角度为观测值，通过加权误差获得的活化函数，实现对当前统计模型参数的调节，实现了对目标转弯机动的位置跟踪，但角速度和角加速度的估计精度还需要进一步提高。文献［10］建立了双层交互多模型，内层为当前统计模型和匀速模型组合，外层为转弯模型，该模型虽然相对于一般交互多模型的精度有所提高，但需要平衡转弯速率变化和滤波角速度偏差之间的关系。文献［11-12］通过交互多模型构建多种特征向量，并利用神经网络实时估计平均转弯率，在一定程度上提高了稳定精度。当前圆周模型通过引入加速度的概念，建立了二阶圆周模型［13］，本文在其基础上，通过引入加加速度的概念提出了三阶圆周模型，并在蛇形机动转换点处设计了基于转换因子的新息数据阈值检测算法和基于新息数据的假设检验算法，有效提高了转换点处的收敛速度和滤波精度。

1 蛇型运动假设与分析

在真实战场上，目标为了躲避炮弹，常常会急加速、急减速以及做转弯机动，给命中目标增加难度。当目标做蛇型机动时，按照现行解命中方法解算，命中概率会大幅降低。在加上射手的心理影响，跟踪精度会下降，留给模型的误差阈量更小，使命中难度进一步加大。建立蛇型运动轨迹如图1 所示。

图1 假定蛇形运动轨迹图

根据匀速圆周运动规律，设其线速度为v，角速度为ω，运动周期为T，跟踪时间为t，α 为双圆圆心连线与x 轴的夹角（0≤α≤π），目标从原点O 逆时针出发做蛇型运动。列出目标在x 轴上的速度和加速度公式如下：

2 二阶圆周模型离散化分析

由于蛇型运动模型是在圆周模型上的进一步发展，因此，蛇型运动模型的离散状态方程推导是在圆周模型的基础上进行的。本文首先分析逆时针圆周模型。

根据圆周模型物理运动规律，可得出其几何关系式：

式中，ω 表示圆周运动的角速度，列出状态方程可得：

进行离散化可得：

同理可得顺时针圆周模型。

3 三阶圆周模型离散化分析

常规二阶圆周模型在卡尔曼滤波状态中只涉及到位置和速度，不涉及加速度，如果仅仅按照对速度求导的方式进行求解加速度，会使得加速度数据引入噪声，产生波动。为此，本章在二阶圆周模型的基础上引入了加加速度概念，从原理上对圆周运动加加速度进行了推导与论证。

图2 加加速度分析图

如图2 所示，设A 点为t 时刻目标位置，B 为△t 时间后位置，R 为半径，弦长AB 为l，va为A 点切向速度，vb为B 点切向速度，aa为A 点加速度，ab为B 点加速度，a 为圆周运动标量加速度，v 为圆周运动标量速度，ω 为角速度，σ 为AB 两点加速度之间夹角。将B 点矢量加速度平移到图中虚线位置，使其起始端与A 点重合，故存在以下矢量关系：

进行离散化可得：

同理可得逆时针圆周模型。

4 基于三阶蛇形机动模型的转换检测算法设计

4.1 基于转换因子的新息数据阈值检测算法

在典型算法中，卡尔曼滤波算法中状态参数矩阵A 是固定的，当目标机动状态和运动模型不相符时，连续使用该状态矩阵进行实时解算，会使误差迭代扩大。为了解决此问题，需找到目标机动的转换点，及时对状态参数进行更新，以提高适应性，为此，本文提出了基于转换因子的新息数据阈值检测算法。在实时解算过程中，当新息值ρ 大于机动目标检测阈值σmin时，就会进行模型转化。转化因子公式如下：

矩阵A 更新公式如下：

其中，（i，j） 的取值分别为（1，3）、（1，4）、（2，3）、（2，4）、（3，1）、（3，2）、（4，1）和（4，2）。

当新息值超出阈值时，顺逆时针状态参数矩阵会进行转换，实现蛇型机动模型反向切换。阈值设置过大，会使局部偏差增大和偏差持续时间延长，设置过小，会使虚警率提高，为此需要找到一个平衡值。随着目标状态参数的迭代，从目标真实机动状态转变到阈值突破点，再到自适应寻优结束，该段时间内会在转换点附近产生一段误差。通过改变阈值的大小，本质就是对滤波值实时性和准确性的折中处理，所以该方法具有一定的局限性。

4.2 基于新息数据的假设检验算法

若要破解或者进一步优化解决实时性和准确性这一难题，需要从方法层面进行优化，在保证实时性的基础上提高准确性。针对该问题，在三阶算法的基础上，提出了基于新息数据的假设检验算法。

在仿真实验中，假设自动跟踪抖动误差符合正态分布，其他系统误差也符合正态分布，总体误差也是符合正态分布的，因此，新息也是符合正态分布规律的，可以以此为突破点，利用假设检验的方式，对机动状态进行快速检测。其中，假设检验的显著性水平为α，时间窗口为n。H0：机动模型没有发生改变；H1：机动模型发生了改变。

上述检验问题的拒绝域为：

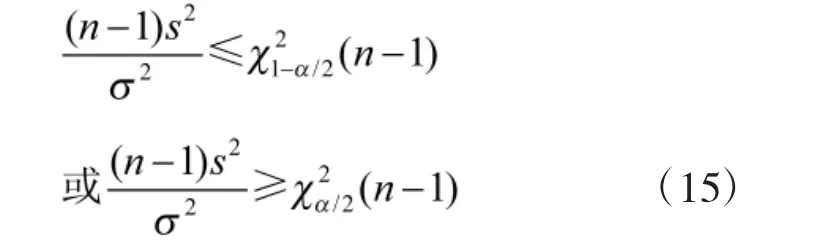
其中，s2是σ2的无偏估计，当H0 成立时，s2与σ2的比值一般在1 附近波动，不会远大于1 或远小于1。

5 仿真结果与分析

在仿真实验中，本文认为模型跟踪误差为零，即认为观察轨迹为真实轨迹，假设某机动目标按照图1 所示的轨迹进行炮弹规避运动，线速度为v=10 m/s，角速度ω=0.05πrad/s，运动周期T=80 s，炮弹出膛时间为t，双圆圆心连线与x 轴的夹角α 为45°（0≤α≤π），目标从原点O 逆时针出发做蛇型运动。

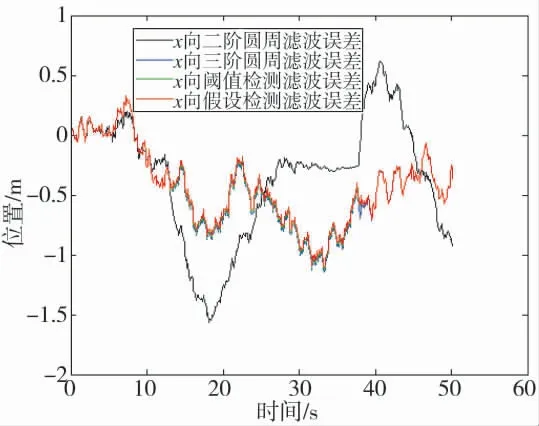
图3 x 向位置误差对比图1

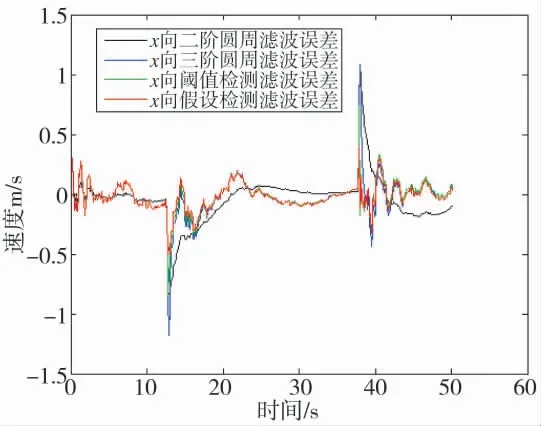
图4 x 向速度误差对比图2

图5 x 向加速度误差对比图3

通过对比仿真分析，结果表明，基于三维圆周模型的卡尔曼滤波算法，优于基于二维圆周模型的卡尔曼滤波算法，基于新息数据的假设检验检测算法，优于基于转换因子的新息数据阈值检测算法。从结果分析，改进算法精度更高，能为战车战斗力提升提供更多理论支撑，具有一定的实用价值。

6 结论

针对水平横向单方向参数的局限性，提出了加入水平纵向状态参数信息，形成双向参数交互方案，进一步提高滤波精度和目标状态间断点的自适应性。在当前已有的二阶圆周模型的基础上，通过引入加加速度的概念，创新性地推导出了三维圆周模型，有效提高全程的滤波精度。针对蛇形机动换向问题，在基于三阶圆周模型的卡尔曼滤波的基础上，提出了基于转换因子的新息数据阈值检测算法和基于新息数据的假设检验检测算法，提高了状态间断点处的检测，即蛇形机动模型转换处的检测灵敏性，并在一定程度上相对提高了收敛速度。

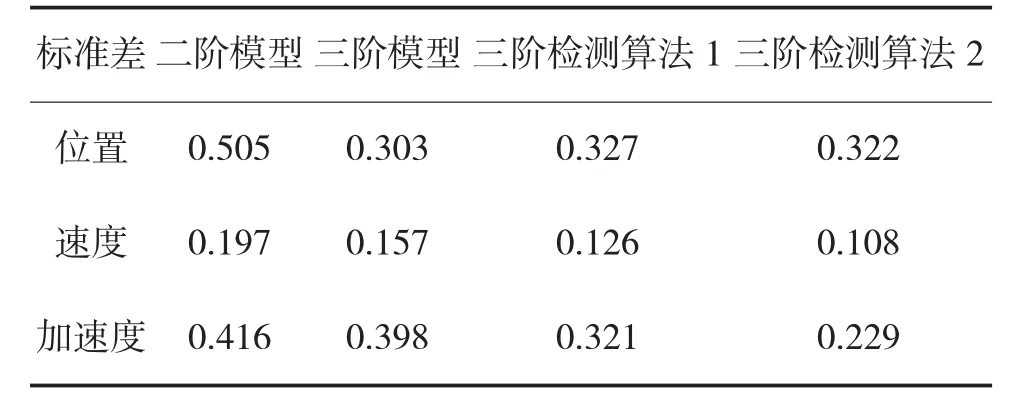
表1 算法误差标准差值对比表