基于小波变换的图像水印处理

刘少伟 戴必翔

摘要：本文对于基于小波变换的数字水印算法进行了比较基础的研究，介绍了水印嵌入算法的预处理步骤，本文提出的水印嵌入算法是在中频部分嵌入水印图像，在水印图像的预处理过程中可以加入Arnold图像置乱算法或不加入图像置乱算法，本文通过两种评估方式来对比实验结果，本文算法在加入图像置乱算法后通过提取算法提取水印图像效果不是很明显，而不加入置乱算法后水印提取完整性很高。

关键字：小波变换;图像置乱处理;峰值信噪比;归一化系数

1引言

随着目前计算机技术及相关产业的发展，图像处理变得越来越普遍，随之图像的加密处理变得越来越重要，与之相关的研究蓬勃发展。因此，数字水印技术应运而生，数字水印技术是一种解决版权保护和信息安全的技术。

目前数字水印技术主要包括空间域[1] 和变换域的水印技术。其中变换域的水印方法包括DFT，DCT和DWT[2]等。由于小波的空频分解特性较好，而且在小波变换域内的图像处理可以充分利用人眼的视觉系统的某些特性，同时又与新一代静止图像压缩标准相互配合，因此，基于小波变换的图像水印处理应用前景较好。

2 小波变换和图像置乱处理

2.1 图像的小波变化

小波变换将图像在独立的频带和不同空间方向上进行分解，能更好地与人类视觉系统相结合，是继傅立叶变换之后又一里程碑式的发展[3]。

在图1，an为低频分量，bn为高频分量的水平延伸，cn是高频分量的垂直延伸，dn是高频分量的对角延伸，且n =1，2，3。其中，小波高频分量为图像的边缘及纹理部分[3]。

2.2 图像置乱处理

数字图像一般需要置乱处理，即指图像位置空间等的变换。

本文使用Arnold 变换，该变换直观、简单、有周期性。在文献[4]中，就讨论了Arnold 变换在数字图像变换中的应用。

Arnold 变换又称猫脸变换，该变换公式为

从采样角度看，数字图像为二维离散点的阵列，即对应一个图像矩阵。对于正方形数字图像，可进行离散化的Arnold 变换[4] 。

通过上式，便可对图像所有像素点位置进行变换，得到置乱后图像。另外要注意，该变换会有周期性。

3 数字水印的性能评估

3.1 峰值信噪比

本文使用均方根误差来度量相关载体图像在嵌入水印后与嵌入前的变化情况。即用均方根误差来对图像质量变化进行评估。

均方差的计算公式（针对二维图像）：

这里f（x，y）是原始图像的像素值，fr（x，y）是添加水印后图像的像素值，M、N 分别是图像的宽和高。

在本文实验中，通过计算峰值信噪比（PSNR）来对图像尺度进行评价。针对普通图像格式，其灰度级别是 0～255，0 代表黑色，255 代表白色，因此 PSNR 的计算公式如下[5]：

对于PSNR取值，一般在20到40分贝之间。本文通过计算两个图像的PSNR来对图像质量进行评估。

本文使用峰值信噪比（PSNR）来估计水印嵌入宿主图像之后含水印图像的扭曲程度，并作为反映一个数字水印算法不可见性好坏的指标。

3.2 归一化相关系数 NC （Normalized Correlation）

从待测图像中提取出数字水印后，常用NC即归一化互相关系数来评估水印嵌入前和提取后的相似度。W 表示原水印图像，W′为提取后水印图像。

M1，M2分别为原水印图像和提取水印图像的宽和高。

归一化相关系数 NC 计算公式如下：

NC的范围为0到1之间，如果NC越接近1，则表示两个图像相似度越大，NC越接近于0，则表示两个图像相似度越小[6]。

4 水印算法的实现

4.1 原始图像和水印图像

本课题使用的原始图像为512*512的彩色图像和64*64的二值水印图像，由于采用彩色图像作为预处理图像，并且彩色图像的索引表不连续，这里将彩色图像转换为灰度图像，灰度图像是指每个像素点可以取0-255这256个整数之中的一个数，数值越小，黑色越深，即0代表黑色，255代表白色，中间值显示递减的灰色。此变换使索引表连续，进而进行小波变换。另外本文采用二值小图像作为研究对象。

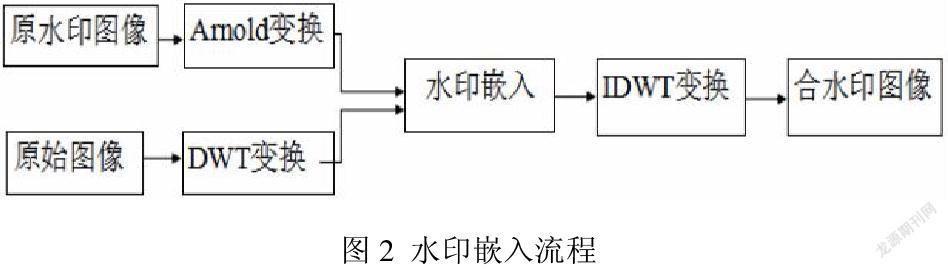
4.2 水印的嵌入算法

读入灰度图像和置乱后的水印图像，对原始图像（512*512）进行分块处理，这里设置每一块的大小为8*8，应注意原始图像的分块个数应大于等于水印的像素个数，按顺序将二值水印每一个像素对应的数值，按照一一对应的关系，根据具体的嵌入算法，嵌入到相对应的原始图像的数据块中。

在水印嵌入算法过程中，需要对原始图像进行dwt小波变换，由于对原始图像进行分块处理，所以需要对图像的每一块分别进行二维二层小波变换，上文已经提到将水印嵌入到图像中频部分是一个比较好的选择，故在此我们将水印嵌入到与之相对应的原始图像块的中频对角线子图部分。

水印嵌入算法具体步骤如下：

（1）对原始水印C采用Arnold变换进行置换预处理，處理后的水印图像为C1。保留置乱次数k作为密钥。

（2）对原始图像进行分块，每一块的大小为8*8，原始图像的分块个数大于等于水印图像的像素个数。

（3）对原始图像的每一块进行二维二层离散小波变换，得到不同分辨率级下的6个细节子图和一个逼近子图，这些图分别对应一个低频子带cA2、三个中频子带（cH2、cV2和cD2）和三个高频子带（cH1、cV1和cD1）。

（4）将水印图像中每一个像素点的信息嵌入到原始图像与之相对应块的中频对角线子图cD2中，当读入水印的一个像素值时，其嵌入方式如下：

当像素值为0时，使中频对角细节cD2（1，1） >cD2（2，2），表示嵌入了黑色的水印像素;

当像素值为1时，使中频对角细节cD2（1，1） <= cD2（2，2），表示嵌入了白色的水印像素;

（5）上述步骤中水印图像中一个像素点嵌入完毕后，再对此像素所在的块进行两层重构处理。得到重构后的块图。

（6）若水印中的所有像素点没有嵌入完毕，重复执行步骤4和步骤5，直到所有像素点嵌入完毕。

下图为水印嵌入算法的流程图：

4.3 水印提取算法

本课题图像中水印具体的提取过程如图3 所示。

水印提取算法具体步骤如下：

（1）首先对嵌入水印后的图像进行分块，块大小为8*8，对每一块进行二维二层离散小波变换，分别得到一个低频子带cA2、三个中频子带（cH2、cV2和cD2）和三个高频子带（cH1、cV1和cD1）。

（2）通过对步骤1中每一块分解所得的对角线中频子带cD2系数矩阵中cD2（1，1）和cD2（2，2）的大小关系，提取水印中的一个像素值，其提取方式如下：

（3）重复步骤2，直到把图像中所有块遍历完毕，提取出置乱后的水印图。

（4）通过Arnold置乱算法对提取后的水印图进行反置乱，得到最终的水印图。

5 实验结果及分析

我们采用原始图像为彩色的dog图（512*512*8），经过灰度处理后，转换为图4（a），以及含有特殊意义的二值图像C（64*64）作为水印，如图4（b）。在Matlab 2013a 和 windows 10 平台上进行仿真实验。对于原始图像，失真度用峰值信噪比（PSNR）进行量化评估，对于提取出的水印用归一化相关系数（NC）进行量化评估，按照上述的方法进行水印的嵌入和提取。不加Arnold置乱步骤结果如下图5所示，加入置乱步骤后结果如图6所示。

图4中图（a）为原始图像，图 4中图（b）为原始水印图像。图 5中图（a）为嵌入水印后的图像，图5中图（b）为未受到任何攻击下提取出的水印图像，计算得到 PSNR=41.3076dB，NC=1。图6为加入置乱算法后得到的图像和水印图，由于相关系数太低，故本算法不适合加入置乱，有待完善。所以这里着重强调不加置乱算法的嵌入和提取即图5。图5说明本文算法（去除置乱后）使水印具有很好的不可见性且水印检测性能稳定。上述图像嵌入和提取是对图像进行中频对角线方向进行处理。下图为是将水印图像嵌入高频对角线子图cD1（不加置乱）。

通过图5和图7进行对比，将水印图像嵌入到原始图像的高频对角线子图，嵌入水印后图像的峰值信噪比为42.4252dB，而若陷入到原始图像中频对角线子图，嵌入后图像的峰值信噪比为41.3076dB，说明嵌入水印后图像的质量相差不多，图像失真度较小。再者是相关系数的比较，图5提取水印与原水印相比，相关系数为1，说明提取后水印和原水印的相似度为百分之百，而在高频中提取水印，相关系数为0.9765，非常接近于1，但是不如在中频中提取出的水印质量好。综上，将水印嵌入到高频和中频区域对原始图像的影响不大，峰值信噪比相近，在相关系数方面，中频提取大于高频提取。所以将水印图像嵌入到原始图像的中频部分是一个比较好的选择。

再者通过图6可知对图像加入置乱算法后，提取后的水印与原水印相似度太低，可能是算法不是很完善，这里我们换一种水印（黑底水印）来尝试加入置乱算法后提取水印的完整性，之前的水印我们称之为白底水印，黑底水印原图和提取图如下：

通过图9和图6进行对比，当加入Arnold置乱算法之后，提取后的黑底水印与原水印的相关系数为0.7629，而提取的白底水印与原水印的相关系数为0.3743，说明本文算法使白底水印具有很好的不可见性但白底水印检测性能稳定较低，使黑底水印具有很好的不可见性且黑底水印检测性能稳定较强。

通过仿真实验来验证本文算法。并且通过图7和图5进行对比，说明将水印嵌入中频是一个较好的选擇。本算法在水印嵌入之前对水印信息进行置乱处理或不进行置乱处理，在原始图像的小波变换域进行水印信息的自适应嵌入，从结果看出，水印信息在嵌入后具有良好的不可见性和相对较好的提取稳健性。

6 总结

本文对于基于小波变换的数字水印算法进行了比较基础的研究，即将小波变换运用于数字水印领域，并通过对水印图像加入Arnold置乱算法对水印进行置乱，并选取合适的水印嵌入位置，通过水印嵌入算法对水印进行嵌入，本文分别进行了包含水印置乱算法和不含水印置乱算法的两种不同情况对不同水印进行嵌入和提取。用峰值信噪比和相关系数进行评估，通过仿真实验进行论证。

参考文献

[1]张春田，苏育挺.信息产品的版权保护技术―数字水印.电信科学，1998，14（12）： 15-17

[2]潘蓉，高有行.基于小波变换的图像水印嵌入方法.中国图像图形学报， 2002， 7（7）： 667-671

[3]刘飞龙.面向应用的数字水印技术研究.博士学位论文.中国科学院自动化研究所，2003年6月

[4]丁玮. 闫伟齐. 齐东旭. 基于 arnold 变换的数字图像置乱技术.计算机辅助设计与图形学

[5]刘瑞祯，谭铁牛.水印能量估计的一般性框架.计算机学报，2001，24（3）： 1-5

[6]牛夏牧.数字水印处理算法与测试研究.博士学位论文.哈尔滨工业大学，2000