辅助元素在中考几何中的应用探究

田成东

摘要：初中几何问题是教与学的难点，也是学生在中考中的失分点。在解决几何问题中，有些题目不能仅仅依靠已知条件就能解决，这就需要改变数学策略，引入辅助元素。采取问卷调查法，对问题进行分析，结果显示为，学生在遇到几何问题探究时，大部分学生显得束手无策，选择放弃或是跳过此类几何问题，也有部分学生随意填写一个答案。因此，对辅助元素在中考几何中的研究就有了实际价值意义，对一线教师在几何体的教学中也有了借鉴作用。

关键词：初中几何;数学策略;辅助元素

一、辅助元素的阐述及其应用价值

（一）辅助元素的阐述

在解决数学问题（主要指初中几何问题）的过程中，往往会遇到许多瓶颈，阻碍着我们的解题进度，增加了解题难度，按照一般的解题途径分析会比较困难，这时我们需要根据题目条件，合理构造辅助元素，建立已知与未知之间的“桥梁”，使问题得以解决。所谓构造辅助元素就是適当增加辅助元素，在几何图形中所讲的辅助元素就是添加辅助线。对于中学生来说，能够合理地添一条辅助线或者多条辅助线（某些难度系数较大的几何问题添加一条辅助线无法解答），则思路豁然开朗，使问题得以求解。

（二）辅助元素在几何问题中的应用价值

数学是一门逻辑性、抽象性较强的科目，一些数学几何问题无法通过题干直接获得结论，需要结合已知条件与隐含条件进行推导，将未知转化成已知。这里所讲的隐含条件，就是合理引入辅助线。引入辅助线的目的，旨在能够为学生提供解题思路，引导学生使用逆向思维，从问题出发对题干进行分析，找到问题与条件之间的联系，把它转化到自己熟悉的知识领域，使问题得以解决。辅助线的引入，有助于培养并提升学生的逆向思维与应用知识的能力。随着教育部门对义务教育进行新课程改革，要求教师在教学中要培养学生的自主探究综合素养，促进学生的全面发展。本文所研究——辅助元素在中考几何中的应用探究，就是为了通过引入辅导元素，帮助学生找到解题方法，激发学生学习兴趣，引导学生自主探究数学学科的奥秘，培养学生数学学科的核心素养，为学生种下学好数学的种子。

二、辅助元素在初中几何中的运用

新课程的改革，对学生的综合素养要求也在不断提升。在中考中，对学生知识能力的考查也更加全面。依照数学学科的属性，几何知识在中考考查中难度系数增大，题型较活。从几个实例中来研究分析：

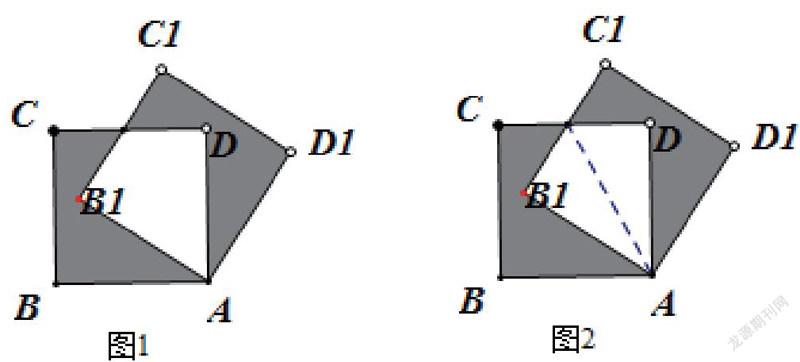
1.[2021铜仁市中考17题]如图1，将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置，则阴影部分的面积是

分析：图1阴影部分的几何图形是一个不规则的几何图形，若要直接求阴影部分的面积，较为困难。通过对题目和图形的分析，结合旋转的知识点，引入一条有效辅助线，就能为解决该几何问题提供思路。如图2，借助辅助线将空白部分的几何图形转化为两个全等的三角形，再运用几何的基本知识，就能求出阴影部分的面积。

2.[2021遵义市中考12题]如图3，AB是⊙O的弦，等边三角形OCE的边CD与⊙O相切于点P，连接OA，OB，OP，AD，若∠COD+∠AOB=180°，AB=6，则AD的长是

分析：这类几何问题就较为复杂，考察了圆与几何图形的联系。这问题，很多学生就会显得束手无策，不知从哪里找突破口。若是平时在联系或者教师在教学活动中有辅助线这一数学思想的渗透，那么解决这类问题或许就有一些思路。如连接OP，过点O作OE⊥AB于点E，过点D作DF⊥AB于点F，如图4所示;利用所作辅助线和题目已知条件可以分别求出OA=OP=OB=，PD=2，证明四边形PEFD是矩形，求出AF，DF，再利用勾股定理求出AD的长。

3.[2020铜仁10题]，如图5，已知正方形ABCD的边长为4，点E在边AB上，BE=1，∠DAM=45°，点F在射线AM上，且AF=，过点F作AD的平行线交BA的延长线于点H，CF与AD相交于点G，连接EC，EG，EF.下列结论：①△EFC的面积为;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是______________________。

分析：主要对②进行分析，如果我们不引入辅助线，可以说这一问在初中几何问题中解起来难度系数非常大，绝大部分同学只能靠猜了。要是能够引入辅助线，问题的难度系数就会降低，能够让更多的学生拿到分数。例如过点F作FQ⊥BC于Q，交AD于P，如图6所示，根据已知条件我们可以得出四边形AHFP是正方形、四边形ABQP是矩形，利用△FPG∽△FQC，可得出线段PG的长度，算出线段AG的长度，再根据勾股定理，在Rt△EAG中，可得出线段EG的长度，从而△AEG的周长就求出来了。

三、辅助元素在初中几何中的研究结论

通过对上述几何问题探讨，使得让我们的教师和学生意识到，合理有效的构造辅助线，在解决数学问题中起到至关重要作用。用构造辅助元素解决问题，可以使学生的数学思想得到渗透、数学思维得到培养、学科综合素养得到提高，进而提高学生分析和解决问题的能力。要想运用好构造辅助元素这种方法，应全面深入分析所给几何图形的特点、条件间的关系以及条件与结论之间的关系，通过对数学问题的综合分析，再合理构造辅助元素。总而言之，辅助元素不仅为学生提供了解题思路，也为学生创造了数学想象的空间，这利于提升学生对几何的探索能力和创新意识的发展，为后续的学习打下夯实基础。

在上述运用中，我们发现有时候所添加的辅助元素不止一条，有两条或者两条以上，一些学生在解决这类问题有了添加辅助线的思想，但是在运用时存在的缺陷就是“怎么加、加哪里、加几条”，要想运用好这种方法是有一定难度的。这就对我们的教师在教学中提出了更高的要求，需要教师们在平常的教学课堂上，能够对某些几何图形进行不同的变换，注重培养学生的几何空间想象能力，让学生见识更多的几何图形，为学生在解决几何问题时提供思路和方法。同时，我们的老师和学生们平时要多积累、多总结、多反思，体会其中的数学原理、数学思想，力求将这种方法广泛应用。通过对学生创造思维能力的培养，让学生数学综合素养能够全面提升，激发学生对数学学习的主动性，促进学生数学核心素养的发展。

参考文献：

[1]魏国军.辅助元素法解决数学问题的探索[J].中学生数理化·学研版，2012（04）：53.

[2]博海伦.构造辅助元素在解决数学问题中的探究[J].解题教学研究，2020（06）：50-52.