基于数据和神经网络的燃气轮机NOx排放预测与优化
2021-01-21朱华昕李苏辉韦晓峰
赵 刚, 朱华昕, 李苏辉, 朱 民, 韦晓峰
(1.郑州燃气发电有限公司,郑州 450010; 2.清华大学 能源与动力工程系,热科学与动力工程教育部重点实验室,北京 100084)
符号说明:
P——机组功率,MW
A——燃烧室振动加速度,m/s2
H——燃烧室压力脉动,Pa
Tamb——环境温度,℃
Tgas——天然气温度,℃
Tout——透平出口温度(OTC),℃
θIGV——压气机进口导叶开度,%
qm,pil——值班火焰燃料质量流量,kg/s
p2——燃烧室进口压力,Pa
qm,pre——预混火焰燃料质量流量,kg/s
pdel——燃烧室压降,Pa
g——重力加速度,m/s2
当环境温度波动时,燃气轮机的NOx排放会偏离正常范围,污染物排放量增加,燃烧稳定性降低。因此,每当季节交替时往往需要对燃气轮机进行燃烧调整,在保证机组安全运行的前提下,尽量减少NOx排放。
燃烧调整前必须要掌握NOx排放与燃气轮机运行参数之间的函数关系,才能在调整时针对性地改变关键参数,使之达标。对于NOx排放与燃气轮机参数之间的关联,已有大量基于物理分析的经验和半经验公式。Lefebvre[1]根据航空发动机燃烧室排放数据得出NOx排放量经验公式,认为影响NOx排放量的主要因素为燃气停留时间、混合速率和化学反应速率。Lewis[2]总结出在贫燃情况下NOx生成量经验公式,认为NOx生成量只与燃烧时的温度和压力有关。Røkke等[3]基于多台燃用天然气的燃气轮机实验数据得出NOx排放量经验公式,认为燃空比和燃烧压力对NOx生成的影响最大。这些研究揭示了燃烧室中影响NOx排放的关键运行参数,但是这些经验公式往往针对某一具体型号或工况,适用范围窄(泛化性能差),如Lefebvre的经验公式仅适用于非预混燃烧的航空发动机,而Røkke等的经验公式没有考虑不同工况下值班火焰(非预混燃烧)燃料与主火焰(预混燃烧)燃料质量流量之间的比例对NOx排放的影响。现代燃气轮机燃烧室往往采用预混燃烧+非预混燃烧的复合燃烧模式,并实时根据燃气轮机负荷调整燃烧模态,在燃气轮机实际运行过程中,NOx生成量受到环境温度、燃烧室压力和各个燃料喷嘴间的流量分配等诸多因素的影响,以往从负荷、当量比、值班火焰燃料与预混火焰燃料质量流量比例及流场组织结构得出的经验公式往往只适合一种工况,不能满足全负荷范围的预测。而且国外的燃气轮机燃烧室对我国保密,很难准确获得其流场组织结构。综上所述,由实验确定的NOx排放规律的泛化性能较差,不能很好地预测特定燃气轮机的NOx排放。因此,在全工况范围确定这些变量与NOx排放量之间的映射关系是燃烧调整的首要任务。
近年来,数据科学与人工智能相结合,为这类多参数、强耦合问题提供了新的解决方法。在电站锅炉的NOx排放预测上,基于数据和人工智能的方法有了很大的发展。Zhou等[4]使用人工神经网络建立了大容量煤粉燃烧锅炉的NOx排放模型,并采用遗传算法优化工况点的NOx排放量。王文广等[5]基于某燃煤机组实际运行数据,利用逻辑门控制循环神经网络建模,成功预测了该燃煤锅炉的NOx排放量。吴祯祥[6]利用最小二乘支持向量机建立模型,该模型可以描述锅炉的NOx排放量与热效率之间的函数关系。王培红等[7]建立了预测电站锅炉NOx排放量、热效率的神经网络与解析函数的混合模型,并利用遗传算法进行燃烧优化。周昊等[8]调用电站锅炉运行数据,利用人工神经网络对锅炉热力参数建模,并实现了操作参数的实时寻优。这些研究都使用电站运行数据训练人工智能模型,得到了NOx排放量与运行参数间的响应特性,再建立优化模型来优化NOx排放量等相关指标。
值得注意的是,燃气轮机的NOx优化应同时考虑燃烧稳定性问题以及NOx排放问题,即保证燃烧室压力脉动(H)和燃烧室振动加速度(A)在运行标准之内的情况下,减少NOx排放,确保机组在给定工况下安全、稳定、清洁地运行。
针对燃气轮机的燃烧调整问题,笔者采用神经网络建立NOx排放预测模型,使用燃气轮机电厂的运行数据训练该模型,并利用训练好的模型对影响燃气轮机NOx排放的运行参数进行敏感性分析,从中选取关键参数,在保证燃烧稳定性的条件下优化NOx排放。
1 NOx排放及燃烧稳定性预测模型
1.1 神经网络结构
图1为单隐藏层神经网络(Artificial Neural Network,ANN)示意图。
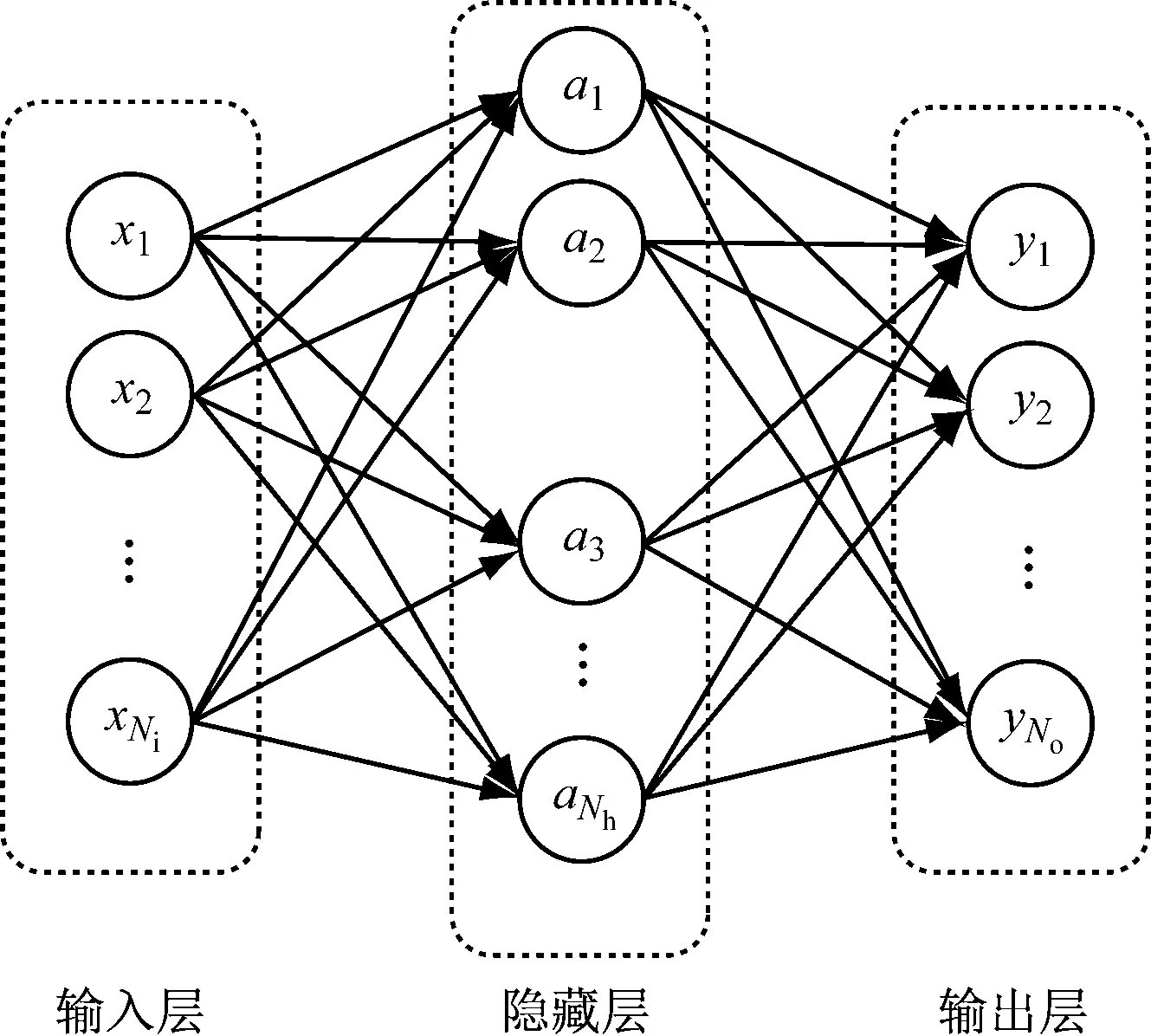
图1 神经网络结构示意图
输入层从x1至xNi共有Ni个神经元,每个神经元的值为数据集的输入变量。对应地,输出层从y1至yNo共有No个神经元,每个神经元的目标值为数据集的输出变量。隐藏层从a1至aNh共有Nh个神经元,将输入数据经sigmoid函数g(x)(式(1))激活后传入输出层。
(1)
以输入层到隐藏层为例,输入隐藏层第i个节点的值xi:
(2)
式中:θi,k为输入层第k个节点到隐藏层第i个节点的权重。
隐藏层的输出为:
ai=g(xi)
(3)
根据上述算法,神经网络从输入层向输出层正向传播,由数据集原始输入数据以及神经元间的权重可以计算出输出层的值,将输出层计算得到的值与数据集中的值进行比较,利用误差反向传播法(BP算法)不断更新神经网络节点连接权重,从而不断缩小模型输出与数据集输出的误差,优化拟合效果。最终的输出模型包含神经网络的结构、神经元激活函数的选取以及神经元间的连接权重。
燃烧稳定性参数由H和A来表征,NOx排放量和燃烧稳定性参数受到环境温度、燃烧室温度和压力、压气机进口导叶(IGV)开度、预混和非预混火焰燃料质量流量等参数的影响。这些参数有强耦合性,对燃烧性能的影响表现出强非线性。因此,燃烧性能具有多变量、强耦合性、强非线性的特点,直接由物理规律推导模型较为困难。针对电站燃烧性能的建模问题,基于大量的电站运行数据,运用神经网络来拟合NOx排放预测模型以及燃烧稳定性预测模型是一个很好的选择。
1.2 神经网络数据集
燃烧性能预测模型示意图如图2所示。选取机组功率(P)、NOx质量浓度ρNOx、A和H4个运行性能参数作为神经网络的输出,环境温度(Tamb)、天然气温度(Tgas)、透平出口温度(Tout)、IGV开度(θIGV)、值班火焰燃料质量流量(qm,pil)、预混火焰燃料质量流量(qm,pre)、燃烧室进口压力(p2)和燃烧室压降(pdel)8个变量作为神经网络的输入。
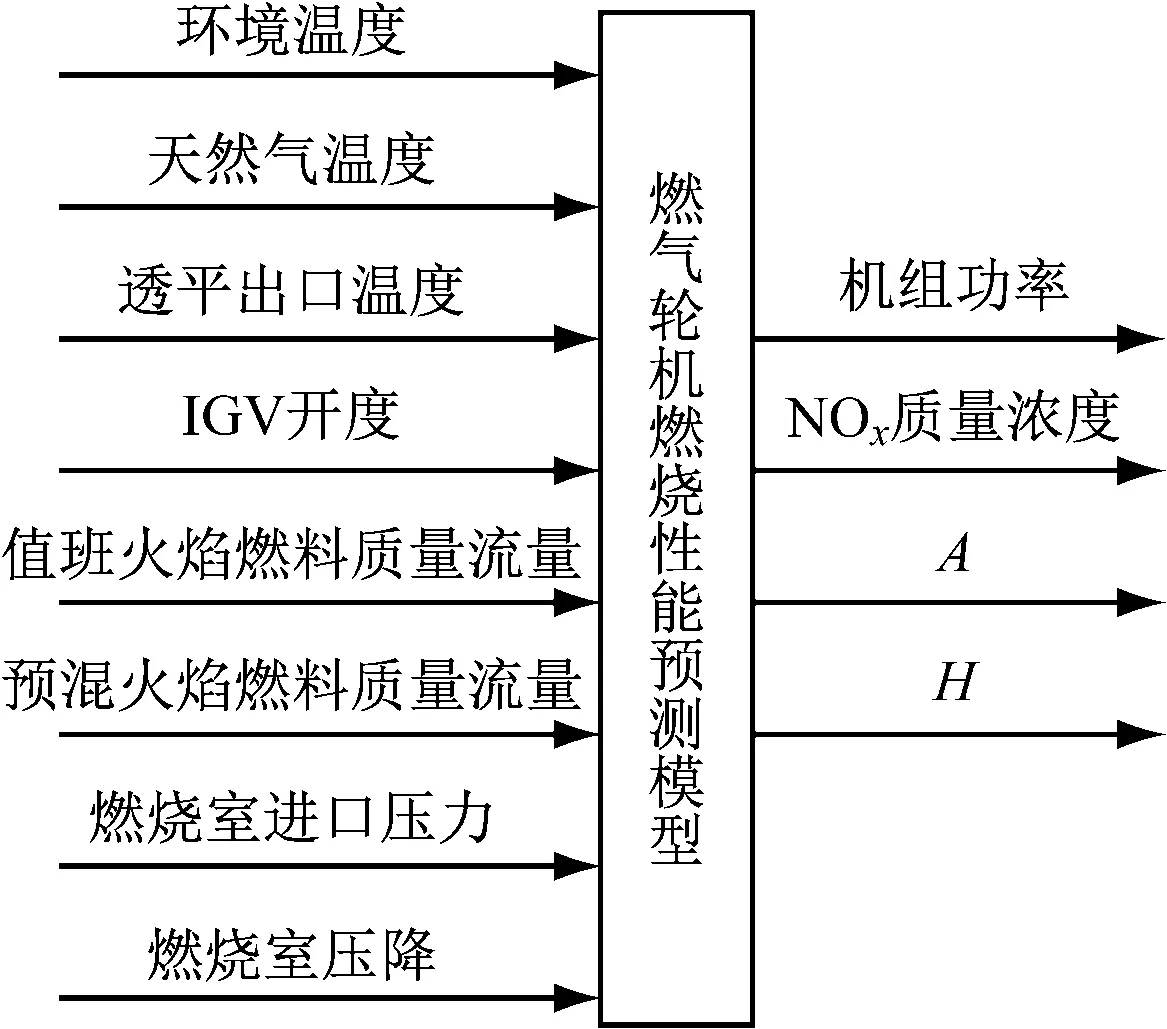
图2 燃烧性能预测模型
图2中的输入、输出向量x,y可表示为:
x=[TambTgasToutθIGVqm,pilqm,prep2pdel]T
(4)
y=[PρNOxAH]T
(5)
除了上述运行参数,很多非稳态扰动对H和A也有影响。如频率就是一个相对重要的参数,不同频率的H和A对燃烧稳定性有不同程度的影响。对于本次建模,由于所提供的电厂数据取样间隔较长,不能准确地捕捉到模型的非稳态特性,加之影响因素多、规律复杂,所以重点研究稳态下的燃烧稳定性,所选参数对燃烧稳定性的预测效果能满足需求。
神经网络的拟合效果不仅依赖于数据集输入、输出特征量的选取,而且与数据量多少有很大关系。一般情况下,数据量越大,模型拟合效果越好,泛化能力越强(不容易过拟合)。
本文所用数据均来自于某V94.3A型燃气轮机机组2018年的实时运行数据,数据点分布如图3所示。
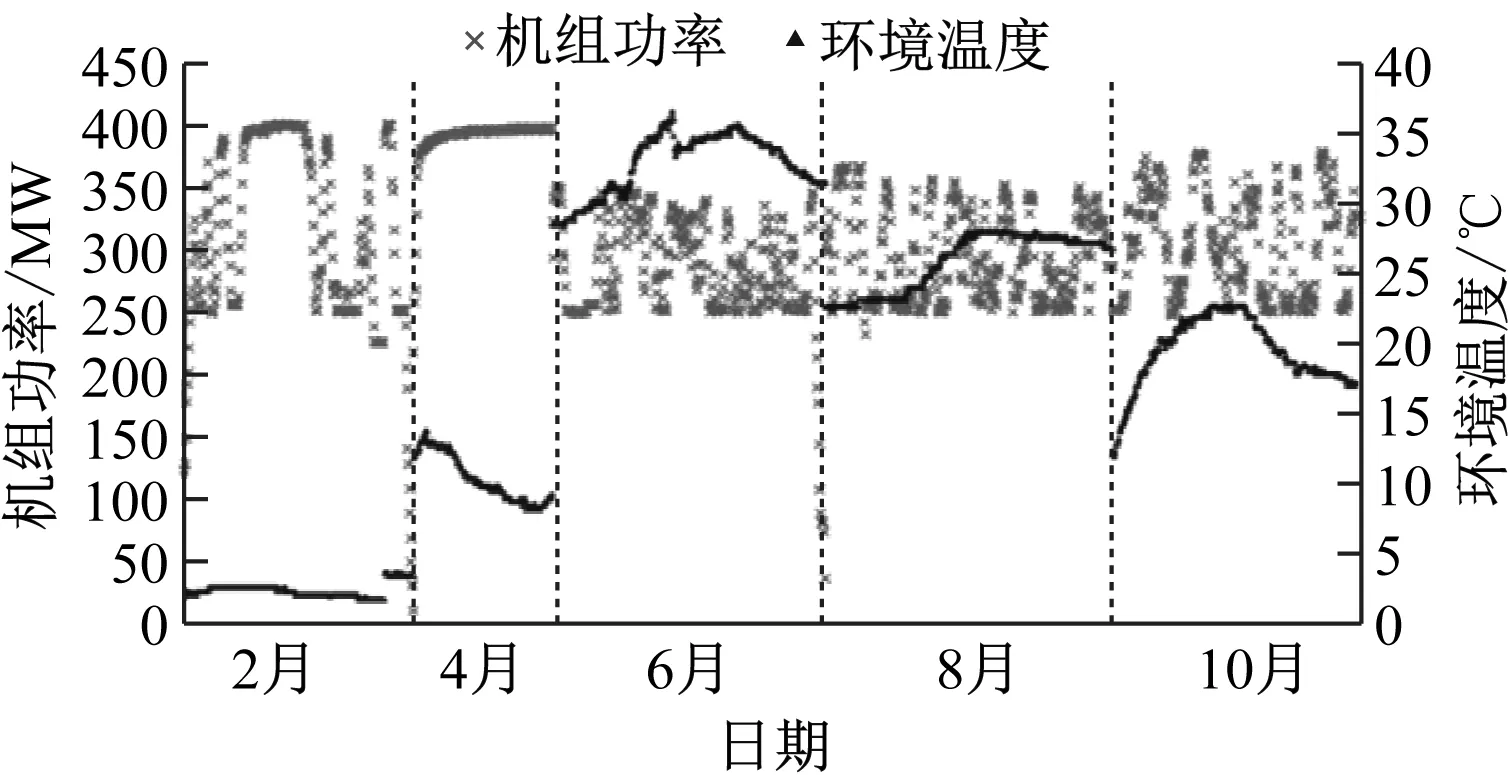
图3 数据集中的机组功率和环境温度分布
图3中有来自不同季节5个月份的1 613个数据点,环境温度变化范围为0~35 ℃,机组功率变化范围为250~400 MW,基本覆盖了燃气轮机运行的所有工况。
1.3 神经网络模型训练
1.3.1 创建神经网络
首先确定神经网络的网络结构,主要包括隐藏层层数、隐藏层节点数、训练算法及各层的传递函数。
理论上,多隐藏层的结构对多变量非线性的映射关系具有更好的拟合效果,但在实际拟合过程中,双隐藏层的神经网络并没有使模型更加精确,反而大大增加了运行时间。可能的原因是单隐藏层已经能够很好地学习到输入输出数据集之间的关系,增加隐藏层层数反而会导致网络过拟合。最终选取的神经网络为传统的单隐藏层神经网络。
隐藏层节点数的选取与隐藏层层数选取类似,增加节点数可以更好地拟合非线性的关系,但是同时增加了过拟合的可能性和时间成本,因此在考虑输入输出特征量个数和确保拟合准确度的条件下,应该尽量减少节点数。最终确定的隐藏层节点数为24。
训练算法是根据误差调节神经网络节点连接权重的算法,选取适合拟合数据的trainlm算法。隐藏层选取sigmoid函数(式1),此函数有很强的学习能力,对于多变量非线性的问题有很好的拟合效果,输出值在(0,1)。输出层选取purelin函数,仅对输入参数作线性输出。
1.3.2 数据预处理
数据预处理包括数据导入、数据分类和数据归一化处理。数据分类将数据集分为训练集、验证集和测试集3部分,分别占比70%、15%和15%。训练集用于更新权重拟合网络,不断提高精度。验证集和测试集用于检验模型对未参与训练的数据的匹配程度,即检验由训练集训练出的模型的泛化能力。通过改变权重提高3个数据集的精度和优化模型。数据归一化处理将输入数据及输出数据全部化归到(-1,1)(见式6),避免由于变量数量级的差异而引起模型不准确。
(6)
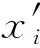
1.3.3 神经网络模型训练
调用Matlab软件的神经网络训练包,运用trainlm算法训练已经搭建的神经网络。通过调整训练目标(均方误差MSE)及迭代次数上限等参数优化神经网络性能。最终发现,增加迭代上限或减小训练目标并没有得到更好的拟合结果,经过60~80次迭代后,训练结果没有明显减小,模型权重也基本趋于稳定。利用该神经网络改变输入变量可以预测不同工况下的燃烧性能参数。
2 模型预测结果及分析
随机挑选数据集中53个数据点的输入向量代入训练好的神经网络中,将预测值与原始数据点输出值(以下简称原始值)进行比较,结果如图4~图7所示。
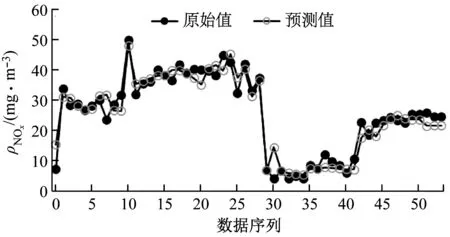
图4 NOx质量浓度预测结果
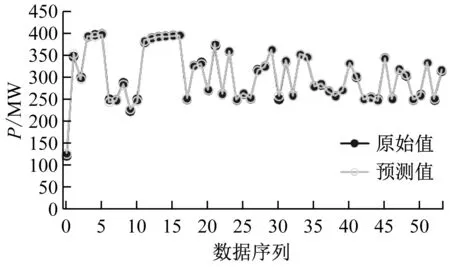
图5 机组功率预测结果
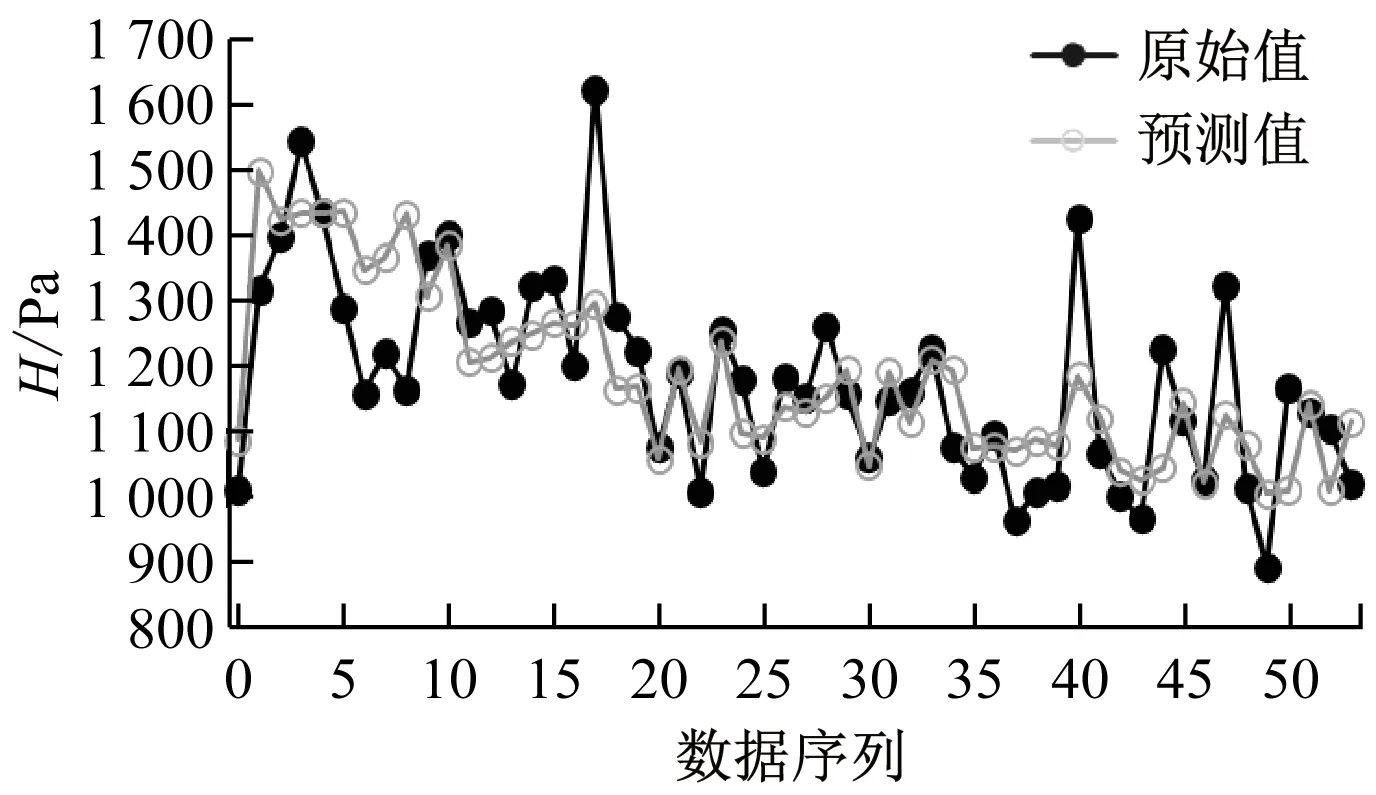
图6 H预测结果
由图4~图7可知,机组功率和NOx质量浓度的拟合结果比A和H的拟合结果好,而同为燃烧稳定性参数的H的拟合结果优于A的拟合结果。
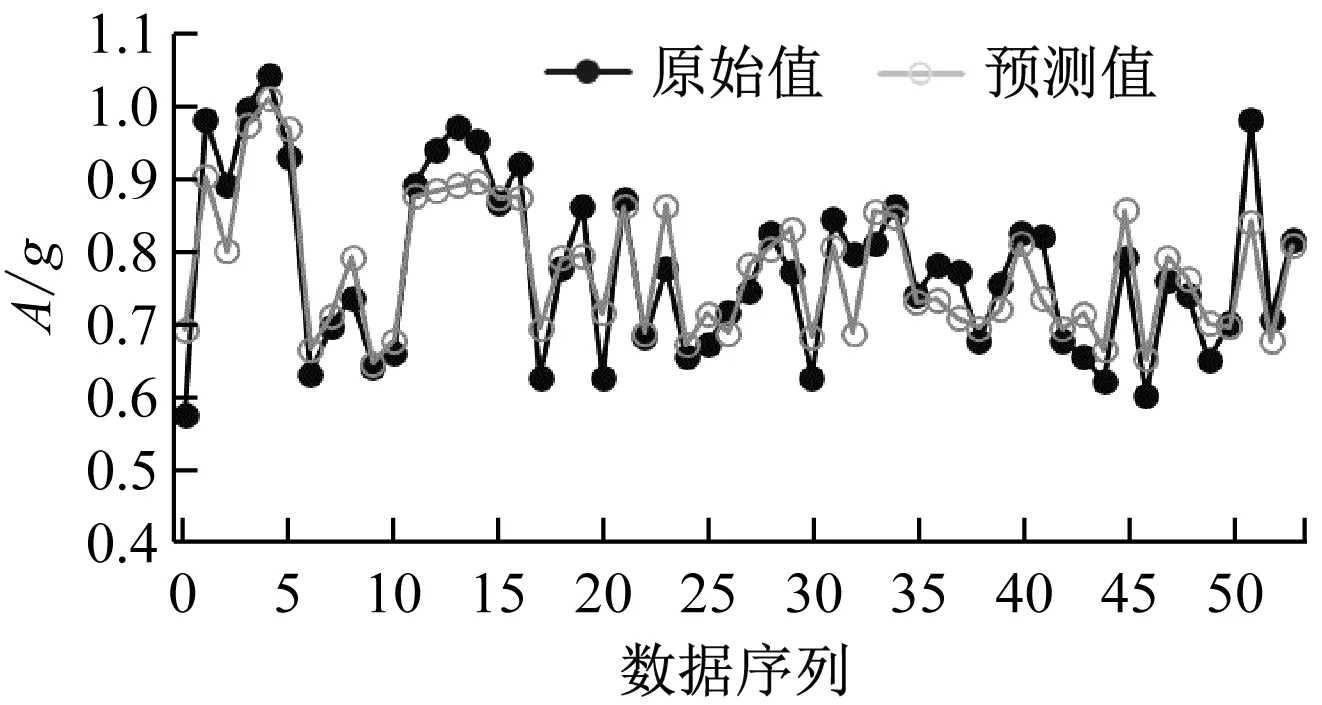
图7 A预测结果
由此可见,8个输入特征量(式(4))可以很好地拟合机组功率,即针对同一机组,在环境温度、燃料质量流量和空气质量流量确定之后,就可以准确地确定机组功率。而NOx质量浓度的拟合效果较机组功率有所欠缺,其原因是NOx的生成机理决定了此变量具有更强的耦合性和非线性,神经网络没能很好地捕捉到这种强耦合性。A和H相较于NOx质量浓度具有更强的耦合性,因此拟合结果相较NOx质量浓度有一定差距。
总体来说,预测值与原始值基本一致。机组功率通过输入变量的简单线性运算即可得到,而NOx质量浓度、A和H的生成机理比机组功率复杂得多,在数据拟合中具有更强的耦合性和非线性,还有进一步优化模型的可能性。
3 模型敏感性分析
3.1 敏感性分析
燃烧优化的目标是使燃烧性能参数保持在燃气轮机健康运行的范围内,因此需要对影响燃烧性能参数的变量进行敏感性分析,确定它们对燃烧性能参数的影响大小及正负相关性。针对已建立的神经网络模型,利用式(7)进行A、H和NOx质量浓度3个参数的敏感性计算。
(7)
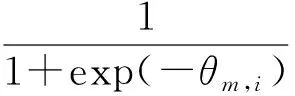
第i个输入变量对第k个输出变量的敏感性因子即为这2个节点通过隐藏层所有节点的乘积之和。将3个变量的敏感性因子整理成图8。
如图8所示,NOx质量浓度对qm,pil、qm,pre和p2的敏感性因子最大,且都为正相关,IGV开度与NOx质量浓度为负相关,这与燃烧物理机理相一致,燃料质量流量和燃烧室压力对燃烧室燃烧状态影响最大,且加大燃料质量流量直接导致NOx质量浓度升高。增大IGV开度即增加空气质量流量,可以有效降低NOx质量浓度。
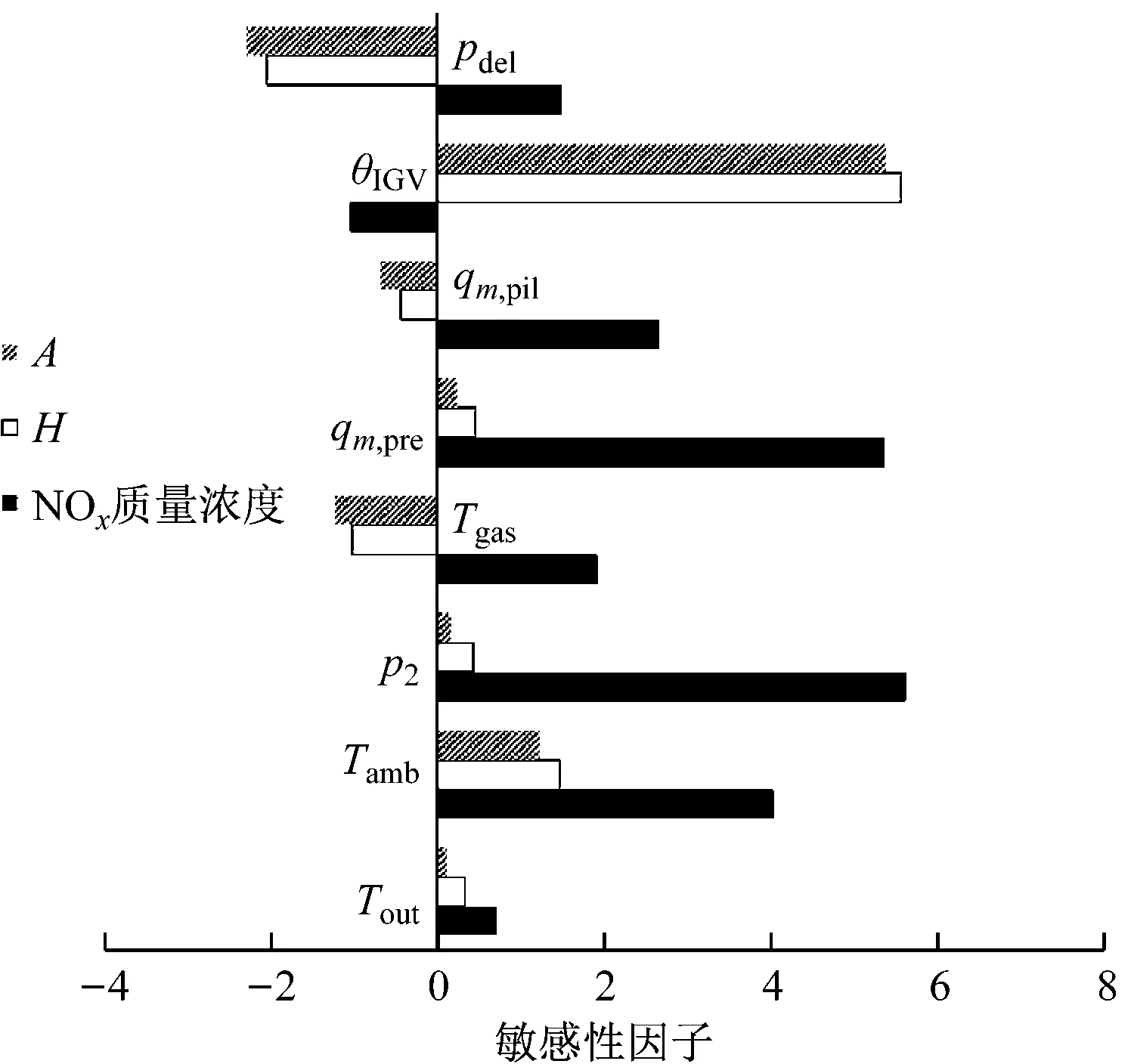
图8 敏感性分析
H与A对8个输入变量的正负相关性保持一致。这符合电站实际运行情况,H和A的变化基本是同时同方向的,对IGV开度、环境温度和燃烧室压降的敏感性最大,其中IGV开度增大会显著增大A和H,可能是由于IGV开度增大使燃烧温度降低,燃烧的稳定性变差。值得注意的是,增加值班火焰燃料质量流量可以减小H和A,原因是值班火焰为非预混火焰,其作用就是稳定火焰。
上述8个输入变量中,Tamb和Tgas为环境变量不可调,Tout、pdel和p2是其他变量的因变量,且不是直接可调的参数。因此,针对NOx排放的优化问题,应着眼于qm,pil、qm,pre和IGV开度3个独立变量的调整。综上所述,NOx质量浓度对燃料质量流量表现出正相关性,对IGV开度表现出负相关性。因此,想要降低NOx质量浓度,需要增大IGV开度或减少燃料质量流量。但是减少qm,pil可能会导致A和H增大,燃烧稳定性变差,而增大IGV开度会同时导致A和H增大。因此,在优化NOx排放的同时要密切关注A和H,避免燃烧稳定性发生恶化。
3.2 基于敏感性分析的NOx排放优化
由于大幅度改变燃料质量流量或IGV开度均会导致偏离原工况点,故要小幅微调相关变量,选取3%的调整范围。选取NOx质量浓度较高的数据点进行优化,优化结果见表1。
由表1可知,不论是哪种调节方式,机组功率的变化均在2%以内,可以认为机组运行工况没有发生明显改变。IGV开度增大3%,机组功率减小3%以及qm,pre减少3%对应的NOx质量浓度分别降低了7.73%、3.20%和15.86%,故3种方式均可有效降低NOx质量浓度,其中减少qm,pre对降低NOx质量浓度最有效。减少燃料质量流量,A和H均减小,燃烧稳定性加强;增大θIGV,A和H分别增大了1.2%和1.7%。
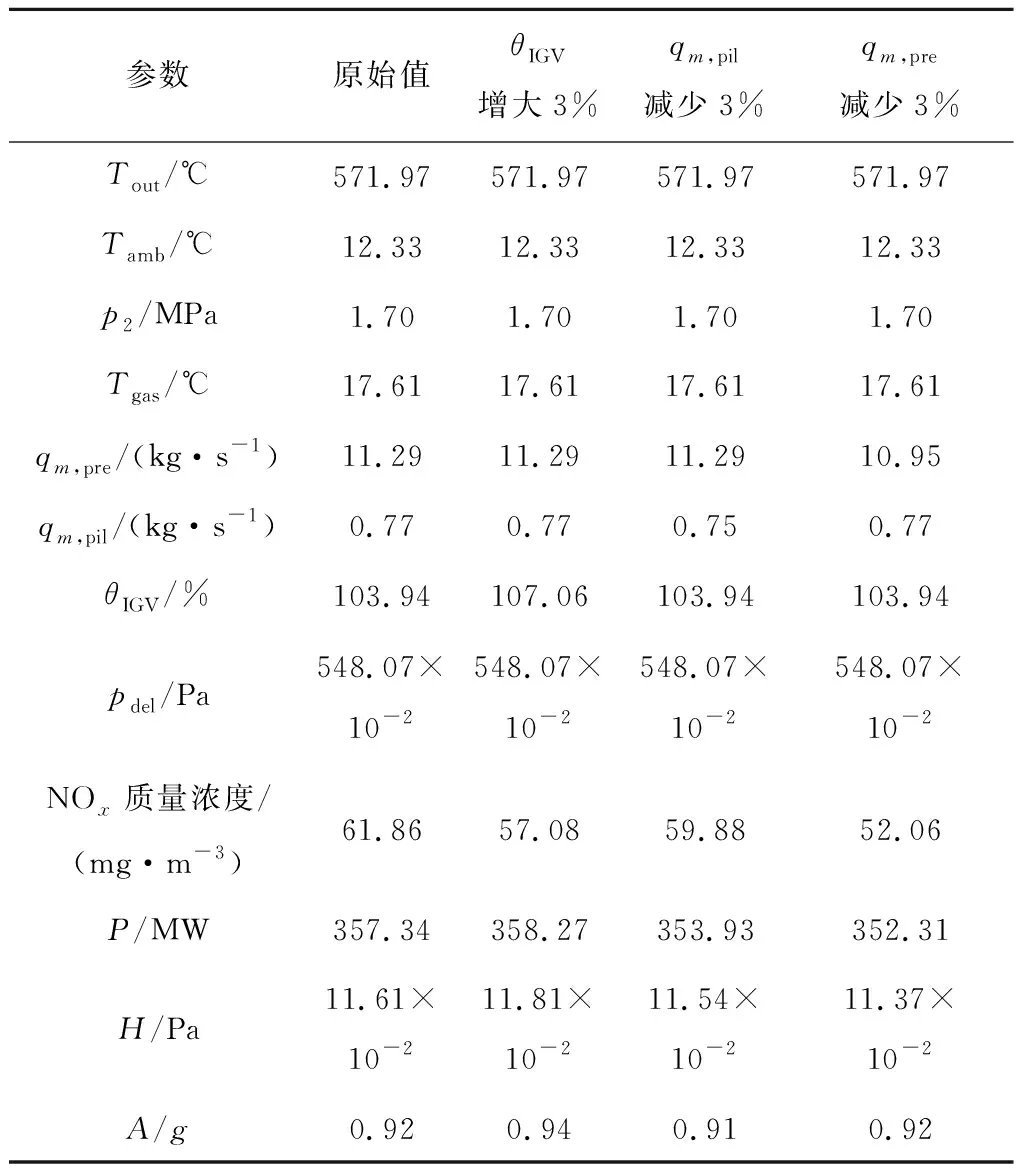
表1 NOx排放优化结果
需要注意的是,为了保证Tout及机组功率达到需求值,燃料质量流量和IGV开度总是同时调整,所以实际情况中NOx排放调节是3种调节方式的耦合。
4 结 论
(1) 所建立的预测NOx排放与燃烧稳定性的神经网络模型的敏感性分析揭示了影响NOx排放和燃烧稳定性的关键因素。
(2) 随着环境温度降低,NOx排放减少,燃烧稳定性变差。NOx质量浓度随值班火焰燃料质量流量和预混火焰燃料质量流量的增加而升高,随IGV开度的增大而降低。与之相反,燃烧室的压力脉动和振动加速度随值班火焰燃料质量流量增加而减小,随IGV开度增大而增大。
(3) 根据敏感性分析结果,对实际工况点参数进行微调,实现了在保持燃烧稳定性的前提下同时降低NOx质量浓度的效果。
