小型热管换热器最优排数的数值模拟研究
2021-01-21李珂欣郑庆红
李珂欣 郑庆红
西安建筑科技大学建筑设备科学与工程学院
本文对应用于高铁车厢内用于空调系统热回收的小型热管换热器进行数值模拟。因为车厢顶部空间的限制,所以分别模拟了2 排管,4 排管,6 排管,8 排管,10 排管和12 排管换热器的换热性能,以便找到一个合适换热器排数,使换热器综合性能达能到最优。
1 边界条件的验证
1.1 边界条件的假设
1)空气的换热过程中不发生相变和化学变化。
2)空气流动视为定常流。
3)换热器壁面视为绝热壁面。
4)流体对流换热处于充分发展段。
5)忽略换热过程中热辐射的影响。
6)根据文献[1-3]中对热管当量热导率的研讨,把热管的轴向导热系数取为10000 W/(m·K)。
1.2 模拟工况的选择
本文在进行数值模拟之前,先对模型的边界条件进行验证,以保证模拟数据的准确性。根据文献[4]中的实验装置参数,利用DesignModeler 建立一个与之相同的模型,再进行四组工况(表1)的模拟,对比实验数据和数值模拟数据见表2,其中,
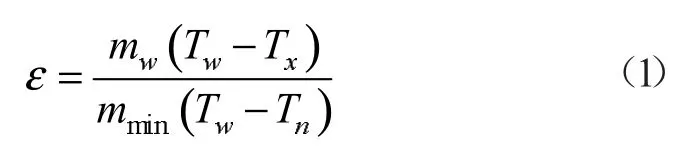
式中:mw为新风体积流量;mmin为排新风体积流量较小值;Tw为室外环境温度;Tn为室内环境温度;Tx为换热后新风温度。

表1 数值模拟工况
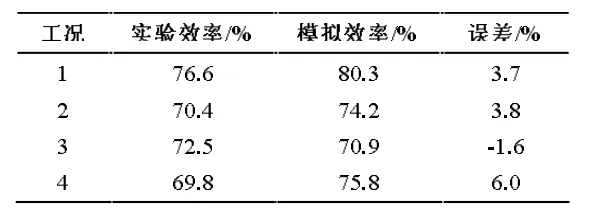
表2 实验数据与模拟数据对比
1.3 实验分析数据和模拟分析数据的对比
实验结果和模拟结果存在较小的误差,其主要原因如下:
1)数值模拟中用等效导热系数来代替热管内部的相变传热过程,但是等效导体的传热过程必然区别于实际情况。
2)数值模拟中只考虑了对流传热和热传导这两项影响因素,未考虑热辐射对传热的影响。
3)数值模拟中换热器的箱体壁面是绝热的,而实际中箱体壁面和外部空气存在换热。
2 模型的建立
2.1 模型的建立与几何参数
本文根据文献[5]武广高铁的CRH1 型空调机组的新排风量(新风量:2120 m3/h;排风量:1700 m3/h)设计了一个12 排的叉排热管换热器,但因高铁车厢顶部的空间较小,所以又研究了6 个不同模型的逆流式气-气热管换热器,其内部单根翅片热管(铝质,工作介质为液氨)的几何参数完全相同,由于热管的叉排排列方式,为了保证逐次增加的热管数相同,因此取排数分别为2、4、6、8、10、12,热管根数分别为11、22、33、44、55、66。几何参数见表3:

表3 热管几何参数表
在翅片管换热器的数值模拟研究中,多位学者[6-10]利用流场的对称性,截取翅片附近的流场建立简化模型进行研究,取得了很好的效果。在本文研究的气-气热管换热器两侧流场内,沿管轴方向流体速度分布较为均匀,故在热管的冷凝段和蒸发段上各选取的一个翅片附近的流域做为研究对象,两侧空气计算域厚度和翅片间距取同值2.2 mm,内含一层翅片。其简域如图1:

图1 翅片附近的简域模型
2.2 网格的划分
因为翅片很薄,所以采取结构性网格,2 排管的网格数量为189414,4 排管的网格数量为713296,6 排管的网格数量为1040158,8 排管的网格数量为1300790,10 排管的网格数量为1654482,12 排管的网格数量为2054322。图2 为单个翅片的网格。

图2 单个翅片的网格
2.3 初始条件及边界条件设置
在利用Fluent 模拟前,需要设置边界条件和初始条件:
1)为了减小入口效应和降低出口处的回流对数值模拟结果的影响,本文将进出口边界进行适当的延长,参照相关研究中[8、11]的处理,把进出口的断面均向外扩展10 倍翅片直径即500 mm。
2)夏季新风入口设置为velocity-inlet,速度大小为3 m/s,温度选取武汉的夏季空调室外干球计算温度35 ℃,排风入口设置与新风相同,温度选取高铁车厢内的温度26 ℃。冬季工况下的风速取值与夏季相同,新风进口温度为武汉的冬季空调室外计算温度-2.6 ℃,排风温度取为20 ℃。空气出口类型均设置为压力出口(Pressure-outlet)。
3)箱体中的热管和空气的传热过程属于流固耦合,因此将流固交界面设置为耦合壁面。
4)箱体中单根热管热导率取为10000 W/(m·K)。
2.4 求解计算
本文选用SIMPLEC 算法进行求解,进行热分析时要用到基本的质量守恒方程,能量守恒方程以及动量守恒方程[12]。采用稳态迭代计算方法,计算完成后,迭代收敛达到10-3以下。
3 计算结果及分析
3.1 管排数对管子壁温的影响
从各个管排数夏季工况下的温度云图(图3)可以看出,随着管排数的逐渐增多,新风出口温度越来越低,其中2 排管的出口温度为32.19 ℃,4 排管的出口温度为31 ℃,6 排管的出口温度为30.01 ℃,8 排管的出口温度为29.4 ℃,10 排管的出口温度为29.08 ℃,12 排管的出口温度为28.73 ℃。同时可以看出,换热器的第2 排管管壁温度随着管排数的增加逐渐升高,从2 排管换热器的30 ℃升到12 排管换热器的33.4 ℃,这是因为换热器内流体的流动方式为逆向流动,2 排管换热器中,新风侧的第2 排管是排风侧的第一排管,温度最低,而对于12 排管换热器,新风侧的第2 排管是排风侧的第11 排管,经过了较长的换热阶段,管壁温度会上升很多,第4,6,8,10 排管也是同样的趋势。所以,增加换热器的换热面积,不能得到相同程度换热量的增量,进而会导致换热器平均到每排管的换热量随着管排数的增加而减小。同理,冬季工况下第2排管子壁温随着管排数的增多而降低。
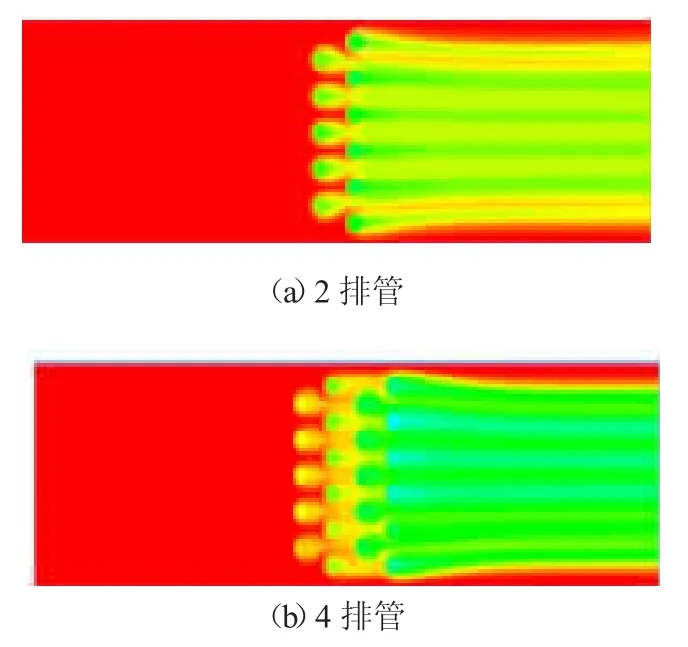

图3 不同管排数的温度云图
3.2 夏季工况下管排数N 对换热性能和压降的影响
本文的夏季室外温度取武汉的夏季空调室外计算干球温度35 ℃,控制车厢内温度为26 ℃,设置Fluent 中新排风的风速V 分别为1 m/s,1.5 m/s,2 m/s,2.5 m/s,3 m/s,3.5 m/s,4 m/s,排数分别为2,4,6,8,10,12,待迭代计算结果稳定后,记录下新风的出口温度T以及换热器的压降ΔP,并计算出不同管排数换热器的总换热量Q 如图4,单位压降的换热量Q/ΔP 如图5,以及单位体积的换热量Q/V 如图6。
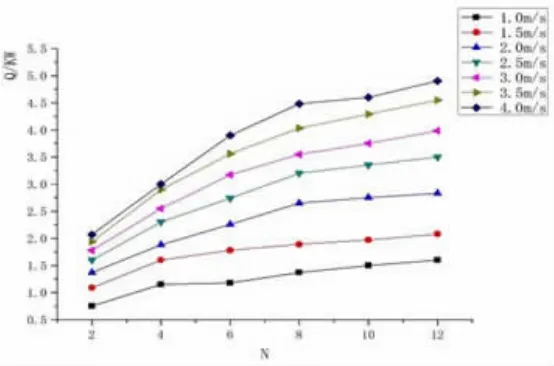
图4 不同管排数的总换热量

图5 单位压降换热量

图6 单位体积换热量
从图4 中可发现,从2 排到12 排,迎面风速一定时,随着排数的增多,热管换热器的总换热量不断升高。迎面风速1.0~4.0 m/s 下,6 排管比2 排管的换热量分别增加了0.43 kW,0.69 kW,0.89 kW,1.14 kW,1.39 kW,1.62 kW,1.83 kW,换热量增加幅度较大,随着管排数再增加,换热量增加的幅度变小。当风速V≤3 m/s 时,10 排管和12 排管的换热量变化很小,风速V=3 m/s 时,4 排管到12 排管换热量增量ΔQ(ΔQ=(QN-QN-2)/(QN-2))分别为43.3%,24.3%,12%,5.6%,6%。同时可以看出,总换热量随着风速的增大而增大,这是因为虽然风速增大会导致换热器箱体内的空气还没来得及换热就流出,会使新风的进出口温差减小,但是由于风速的增大,新风的流量随之增大,导致总换热量还是呈增大的趋势,6 排管时,1.0~4.0 m/s 的换热量Q 分别为1.18 kW,1.74 kW,2.26 kW,2.74 kW,3.17 kW,3.56 kW,3.9 kW。
从图5 中可看出,迎面风速一定时,随着管排数的增加,单位压降换热量逐渐减少,直到10 排以后,单位压降换热量减少幅度很小,这是因为随着管排数的增加,虽然换热器的总换热量增加,但是阻力压降也逐渐增加,而且压降增加幅度大于换热量增加幅度。2排管时,1.0~4.0 m/s 风速下,单位压降的换热量依次为30.0 W/Pa,27.89 W/Pa,25.65 W/Pa,19.28 W/Pa,17.62 W/Pa,16.3 W/Pa,14.89 W/Pa,6 排管时,1.0~4.0 m/s 风速下,单位压降的换热量分别为13.11 W/Pa,12.45 W/Pa,11.32 W/Pa,10.6 W/Pa,9.91 W/Pa,9.3 W/Pa,8.72 W/Pa,下降到2 排管的一半左右。增加管排数,虽然总换热量增大,但是阻力的增加也会增加相应的制造成本,而且也没有得到相应的收益。
从图6 中可以看出,风速一定时,随着管排数的增大,单位体积换热量逐渐减小,2 排管时,1.0~4.0 m/s风速下的单位体积换热量分别为33.0 kW/m3,47.01 kW/m3,60.09 kW/m3,64.38 kW/m3,75.07 kW/m3,84.91 kW/m3,88.46 kW/m3,6 排管时,1.0~4.0 m/s 风速下单位体积换热量分别为17.72 kW/m3,26.3 kW/m3,33.93 kW/m3,41.14 kW/m3,47.6 kW/m3,53.45 kW/m3,58.56 kW/m3,下降到了2 排管的60%左右。增加管排数,换热面积和体积都会增大,但换热量并没有相同程度的增加,又由于车厢顶部的空间限制,不仅总换热量要较大,换热器单位体积的换热量也应该较大,所以排数不能过多。
3.3 冬季工况下管排数对换热性能和压降的影响
本文的冬季室外温度取武汉的冬季空调室外计算温度-2.6 ℃,控制车厢内温度为20 ℃,设置Fluent中新排风的风速V 分别为1 m/s,1.5 m/s,2 m/s,2.5 m/s,3 m/s,3.5 m/s,4 m/s,排数分别为2,4,6,8,10,12,待迭代计算结果稳定后,记录下新风的出口温度T 以及换热器的压降ΔP,并计算出不同管排数的总换热量Q 如图7,单位压降的换热量Q/ΔP 如图8,以及单位体积的换热量Q/V 如图9。

图7 不同管排数的总换热量
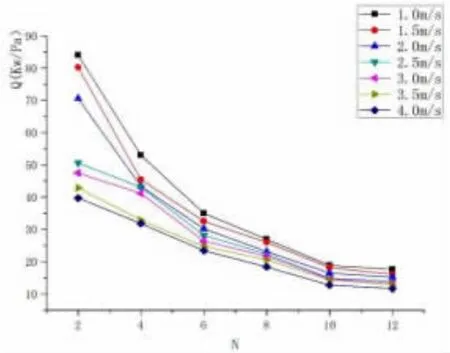
图8 单位压降换热量

图9 单位体积换热量
从图7 中可发现,冬季总换热量随管排数的变化趋势与夏季基本一致,风速不变时,随着管排数的增加,总换热量逐渐增加。由于冬季的室内外温差比夏季大,因此总换热量比夏季多。迎面风速1.0~4.0 m/s下,6 排管比2 排管的换热量分别增加了1.05 kW,1.63 kW,2.32 kW,3.08 kW,3.64 kW,4.39 kW,4.94 kW,换热量增加幅度较大,6 排到12 排,换热量增加的幅度逐渐变小。风速V=3 m/s 时,4 排管到12 排管换热量增量ΔQ(ΔQ=(QN-QN-2)/(QN-2))分别为43.8%,22.3%,15%,5.2%,4.0%。同样可看出,管排数一定时,换热器的总换热量随着风速的增大而增大,6 排管时,1.0~4.0 m/s 风速下的换热量分别为3.15 kW,4.65 kW,6.02 kW,7.28 kW,8.44 kW,9.49 kW,10.46 kW。
从图8 中可看出,冬季单位压降的换热量变化趋势与夏季几乎一致,随着管排数的增多,单位压降换热量逐渐减少,其中10 排到12 排的单位压降换热量变化很小。1.0~4.0 m/s 风速下,2 排管的单位压降换热量分别为84.0 W/Pa,80.23 W/Pa,70.56 W/Pa,50.6 W/Pa,47.52 W/Pa,42.86 W/Pa,39.71 W/Pa,管排数增加到6 排时,单位压降换热量大概已经降到了2 排管的50%,分别为35 W/Pa,32.52 W/Pa,30.15 W/Pa,28.16 W/Pa,26.38 W/Pa,24.78 W/Pa,23.4 W/Pa,8 排管到12 排管,单位压降换热量已经低于2 排管的50%,其中12 排管降到了2 排管的25%左右,压降的增加量远大于换热量增加量,换热器综合性能急剧降低。
从图9 中可看出,冬季单位体积换热量的变化趋势与夏季相同,随着管排数的增多,单位体积换热量呈明显的减少趋势。1.0~4.0 m/s 风速下,2 排管的单位体积换热量分别为86.9 kW/m3,120.36 kW/m3,159.98 kW/m3,181.62 kW/m3,202.99 kW/m3,220.51 kW/m3,235.9 kW/m3,管排数增加到6 排时,单位体积换热量降到了2 排管的60%左右。管排数从6 排管增加到12排管,换热器的体积和换热面积增加了一倍,但是总换热量却只增加了20%左右,增加管排数,换热面积和体积都会增大,但换热量并没有相同程度增加,又由于车厢顶部空间限制,不仅总换热量要较大,换热器单位体积换热量也应该较大,所以排数不能过多。
4 结论
1)不同管排数的换热器,迎面风速一定时,夏季工况下,第2 排管子的壁温随着管排数的增多而增大,冬季工况下,第2 排管子的壁温随着管排数的增多而减小,其他管排的管子也和第2 排管子变化趋势相同。
2)当热管换热器迎面风速一定时,换热器的总换热量随着管排数的增多而增大。其中,2 排至6 排增加的幅度较大,6 排至12 排增加的幅度逐渐减小。换热器的单位压降换热量随着管排数的增多而减小,6 排管换热器的单位压降换热量降到2 排管换热器的一半左右。换热器的单位体积换热量随着管排数的增多而减小,6 排管换热器的单位体积换热量降到了2 排管换热器的60%左右。
3)根据以上的结论,考虑到车厢顶部的空间限制和换热器的综合性能,本文设计工况下热管换热器的最佳排数取为6 排。
