昆仑山地区冻融土导热系数试验测试与预测模型研究
2021-01-21刘志云崔福庆
刘志云,张 伟,王 伟,崔福庆,2
(1.长安大学地质工程与测绘学院,陕西 西安 710054;2.中交第一公路勘察设计研究院有限公司高寒高海拔地区道路工程安全与健康国家重点实验室,陕西 西安 710065)
青藏高原作为特殊的构造集合体,发育了极其复杂、恶劣的冻土工程地质环境。多条线性工程贯穿于其中,构筑物的修建改变了冻土温度场及地气间的热交换条件,在全球变暖趋势的影响下,多年冻土处于劣性动态平衡甚至退化过程[1-3]。导热系数作为重要的热物性参数,反映土壤能量状态及传递、储存热量的能力,是评估外界热扰动影响冻土热状况及所处状态的一个重要因素。
土体导热系数研究工作发展多年,取得了不少成果。在测试方法上,依据测试原理和应用范围主要有稳态法和瞬态法,徐敩祖等[4]采用稳态法和瞬态法测定了多种冻融土导热系数及比热容,并提供了较为完整的用于工程稳定性评价及热工计算的冻土热参数表。随着理论及技术的发展,许多学者[5-9]侧重对导热系数测试方法进行改进及测试系统的研发,应用于不同的试验以增强测试过程的匹配性和适应性。在导热系数影响因素上,研究者主要集中于含水率、干密度、温度、孔隙率等对导热系数的影响,如文献[10-12]指出导热系数与含水率、干密度呈正相关性,但增长过程随两者的变化而不同;温智等[13]通过试验发现原状冻土导热系数随含冰量增加呈线性关系增加。在计算模型方面,不少学者根据导热系数实测数据建立了参考模型,Johansen[14]依据前人大量试验数据提出了以饱和与干土状态导热系数为基础的基于饱和度的计算模型;Coté等[15]在Johansen模型的基础上考虑了诸影响因素的作用,提出了适用范围更广的几何平均法;Zhu 等[16]给出了由各组分导热系数组合的串、并联形式体积加权和指数加权平均的三种导热系数计算模型,对比实测数据偏差较大;罗斯琼等[17]考虑局地影响,整合前人方案发展了适用于青藏高原中部土壤热导率的参数化方案;李顺群等[18]从微观角度出发,建立了聚合模型和混合流导热系数计算方法,为不同负温环境冻土导热系数预测提供了方法;戚家忠等[19]和洪涛等[20]则根据研究土性拟合了导热系数与影响因素间的经验回归方程。同时,不少研究者[21-23]借助神经网络验证了预测导热系数的可行性与精确性,如Bang 等[23]对比分析了线性回归、决策树、支持向量机、高斯过程回归、人工神经网络及深度信念网络等多种方法在导热系数回归模型方面的预测性能,证明了机器学习方法良好的预测性能,引入更多的可行性预测模型。
青藏高原工程走廊带是我国具有多重战略意义的进藏运输生命线,其部分线路穿梭于工程条件恶劣的冻土区,给现有构筑物的养护及新规划线性工程带来诸多难题。本文以青藏高速格尔木—拉萨段工程地质勘察项目为依托,对取自昆仑山区典型多年冻土试样进行室内重塑并采用瞬态平面热源法测试了冻融土导热系数,分析了导热系数分布规律,建立了经验拟合公式、支持向量回归(SVR)和径向基(RBF)神经网络预测模型,以期为修筑于该区域的工程提供热工参数选取参考。
1 试验设计
1.1 试样来源
本次测试土样取自青南—藏北高原昆仑山典型多年冻土区,青藏公路沿线里程桩号K2878—K2919段,钻孔取样路线见图1所示。取样钻孔深度自地表至地下达47 m,天然密度范围1.42~2.5 g/cm3,天然含水率范围1.6%~148.2%,共计土样354组。考虑到土样成分、粒径和饱和度及测试试样尺寸,故分别测试冻土土样349组,融土土样245组。具体测试土类统计及其基本物性参数分别见图2、表1。
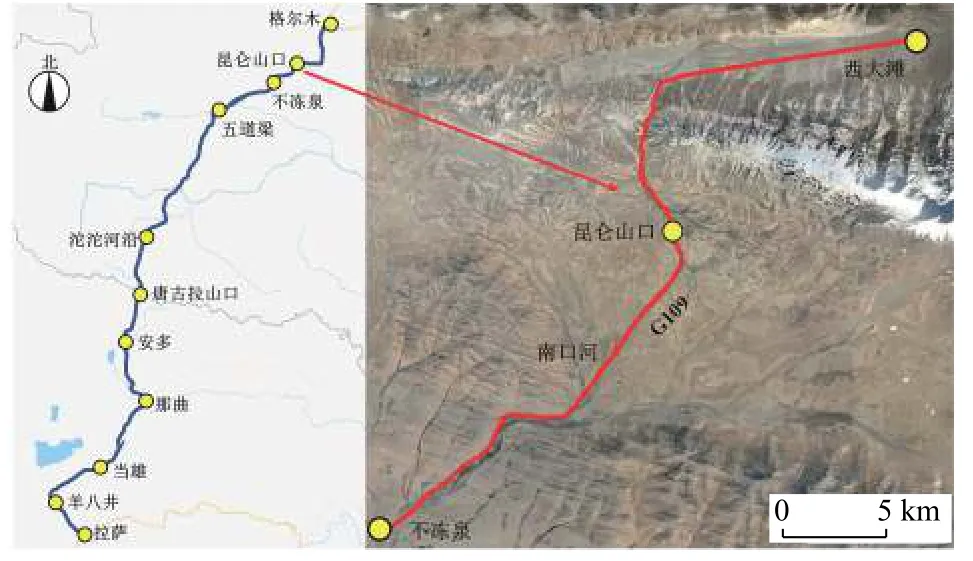
图1 钻孔取样路线Fig.1 Drilling sampling route

图2 土样分类统计Fig.2 Soil sample classification statistics

表1 土样基本物性参数Table1 Basic physical parameters of the soil samples
1.2 试验仪器
本次试验采用Hot DiskTPS1500 测试仪,以瞬态平面热源法测定冻融土试样导热系数,该法具有直接测量热传播、节约时间、受接触热阻影响小及测试试样要求低等优点,具体参数见表2。试验装置由Hot DiskTPS1500 测试仪、土试样架及恒温箱等组成。

表2 Hot Disk 测试仪参数Table2 Hot Disk tester parameters
1.3 试验步骤
沿线钻取土样现场测定天然密度及含水率,封装带回实验室进行室内重塑试验,过程依据《土工试验方法标准》,主要涉及制样、预处理及热物性测试三步骤。所用Kapton 传感器为圆形探头,为提高测试精度,将样品制成直径80 mm、高30 mm的圆柱形试样,该过程需借助制样器、液压机脱模。测试过程需将Kapton 探头夹于表面平整的试样间并固定于样品架中,其中融土试样测试在常温环境中进行,冻土试样测试过程则相对复杂,需预冻、平整化处理并置于恒定负温环境。冻融土试样导热系数测试过程及流程见图3、图4所示。
2 结果分析
2.1 土性分布及导热系数规律分析
图5表明昆仑山多年冻土区测试土样涉及五大类土,其中黏土类占比最多,为31.23%;其次为碎石土类和砂土类,分别占22.92%和19.20%;而全风化岩类和粉土类占比相对较少,分别为15.76%和10.89%。本次沿线跨42 km 随机性系统取样,结果与文献[24]中昆仑山区钻孔勘察岩土性结果基本一致,主要以黏性土类、砾石土类及砂土类居多,整体可反映取样带地形地貌构造下的岩土性分布。
由图6(a)中各类土冻土导热系数频率分布可知,整体分布趋势为黏土类、粉土类、全风化岩类、砂土类及碎石土类依次偏右分布,表明冻土导热系数主要分布范围值依次增大。为排除由取样随机性引起的统计误差,取累计分布概率10%~90%范围导热系数为对比值,统计黏土类主要分布区间为1.500~2.361 W/(m·K),均值为1.885 W/(m·K);粉土类主要分布区间为1.642~2.519 W/(m·K),均值为2.049 W/(m·K);全风化岩类主要分布区间为1.345~2.577 W/(m·K),均值为1.942 W/(m·K);砂土类主要分布区间为1.555~2.741 W/(m·K),均值为2.222 W/(m·K);碎石土类主要分布区间为1.255~2.580 W/(m·K),均值为2.149 W/(m·K)。由各类土冻土导热系数主要分布区间的分布特征可发现,冻土导热系数整体依砂土类、碎石土类、粉土类、全分化岩类及黏土类减小分布,结果与图5冻土均值统计特征相符。

图3 Hot Disk 导热系数测试系统Fig.3 Hot Disk thermal conductivity test system
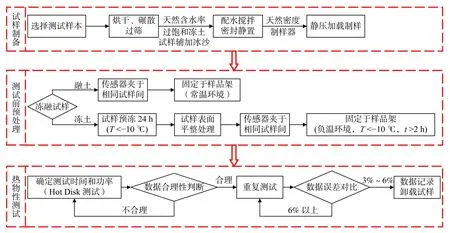
图4 导热系数测试流程图Fig.4 Flow chart showing the thermal conductivity test
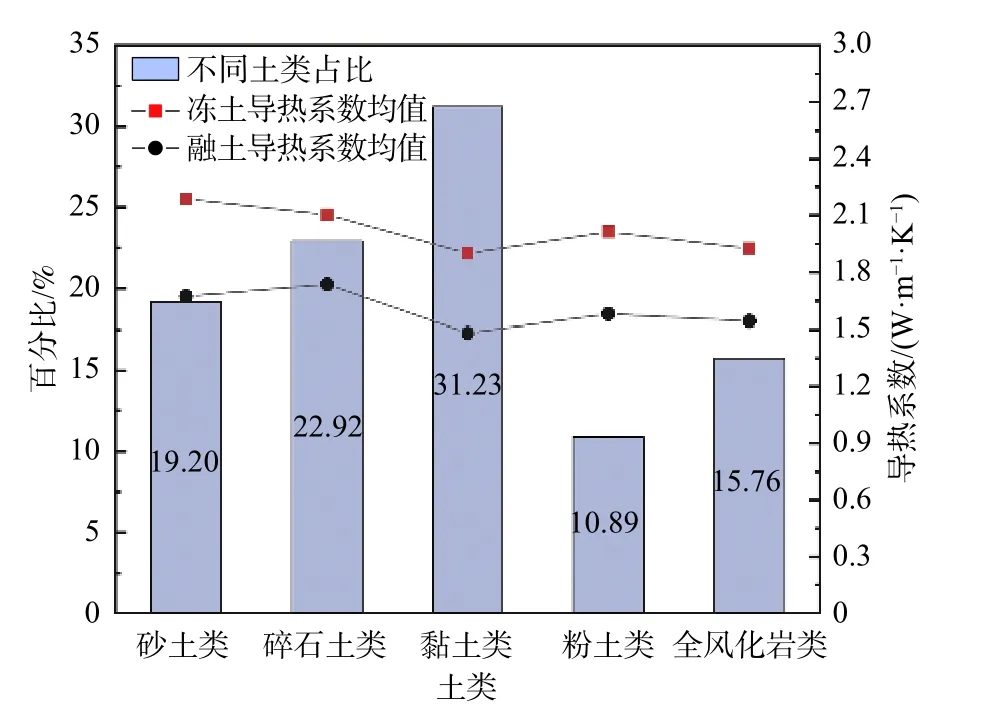
图5 土类占比及导热系数均值Fig.5 Soil percentage and average thermal conductivity
同理,图6(b)中五类土融土导热系数对应凸峰依全风化岩类、黏土类、粉土类、砂土类和碎石土类向导热系数值增大方向偏移,即融土导热系数主要分布范围值依次增大。同样取融土导热系数累计分布概率10%~90%区间作对比,黏土类主要分布区间为1.254~1.771 W/(m·K),均值为1.471 W/(m·K);粉土类主要分布区间为1.362~1.816 W/(m·K),均值为1.565 W/(m·K);全风化岩类主要分布区间为1.256~1.927 W/(m·K),均值为1.542 W/(m·K);砂土类主要分布区间为1.285~2.006 W/(m·K),均值为1.683 W/(m·K);碎石土类主要分布区间为1.220~2.099 W/(m·K),均值为1.749 W/(m·K)。同理,各土类融土导热系数主要分布区间特征表明,融土导热系数整体依碎石土类、砂土类、粉土类、全分化岩类及黏土类减小分布,结果与图5融土均值统计特征相符。
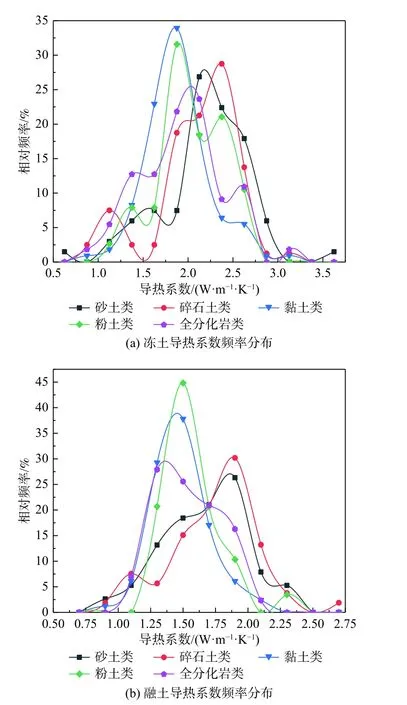
图6 土样导热系数频率分布Fig.6 Frequency distribution of thermal conductivity of the soil samples
由图5并结合以上特征分布分析,可发现粗颗粒土(砂土类和碎石土类)冻融土导热系数整体呈大于细颗粒土(粉土类、黏土类和全风化岩类)冻融土导热系数特征,即土壤质地越粗,导热系数值越大。究其原因,粗颗粒土比表面积小,持水性相对较弱,存在更多自由水附于孔隙之间,从而更能增强土颗粒之间的凝聚连通性,导致热阻减小,表现为导热系数相对较大。
2.2 导热系数影响因素分析
导热系数作为土体固有物理参数,是表征土体热物特性的有效参考,是干密度、含水(冰)率与温度的函数,也与土性及结构相关。研究表明土体导热系数在正负温情况下,温度变化对导热系数的影响较小,故对土体导热系数只区分正负温度影响。根据试样测试环境温度的差异得冻土及融土导热系数,故导热系数主要受干密度与含水率影响。因沿线取样的随机性,试样物性参数分布规律性差且含水率与干密度具有显著的负相关性,故采用偏相关分析方法分别剔除含水率、干密度影响,分析二者与导热系数的净相关性。
由表3中导热系数与含水率偏相关性分析可知,五类土整体均表现为二者呈正相关,其中粗颗粒土(砂土类、碎石土类)冻融土显著性结果均低于0.05,表明两种土类冻融土导热系数与含水率呈显著线性相关;同时,黏土类冻土及全分化岩类融土导热系数与含水率也体现显著线性关系。其余土类导热系数与含水率线性关系较弱,可能与土类不同含水量及水分形态状态下,导热系数随含水率变化规律不同有关,故整体表现为非线性正相关关系。
同理,导热系数与干密度偏相关性分析表明,五类土整体亦表现为该二者呈正相关性,其中碎石土类和黏土类冻融土显著性结果均低于0.05,表明两种土类冻融土导热系数与干密度呈显著线性相关;同时,砂土类和全分化岩类融土导热系数与干密度也体现显著线性关系。其余土类导热系数与干密度呈较弱线性关系,可能与土类处于不同矿物骨架紧实状态下,导热系数随干密度变化规律不同有关,因而不同土类整体呈现非线性正相关性。
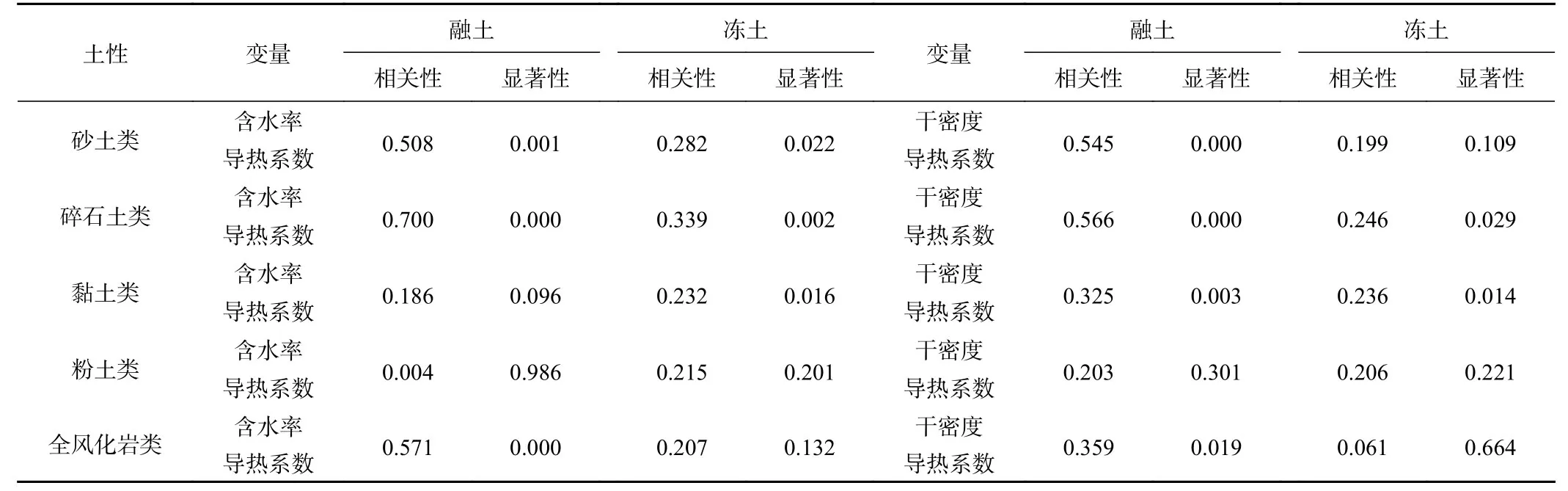
表3 导热系数与含水率、干密度偏相关分析Table3 Partial correlation analysis of thermal conductivity with moisture content and dry density
3 导热系数预测方法研究
3.1 导热系数经验公式拟合
结合以上偏相关性分析以期找到可反映导热系数与含水率、干密度间变化规律的数学表达式,故对五大类土各取样本量较多的典型土类进行经验回归公式拟合。由表4中各种土经验公式可发现,导热系数与含水率、干密度间关系因土性差异拟合形式不同,但均表现为非线性拟合结果。表4各公式中的参数取值见表5。

表4 各种土二元经验回归拟合结果Table4 Binary empirical regression fitting results for all kinds of soil
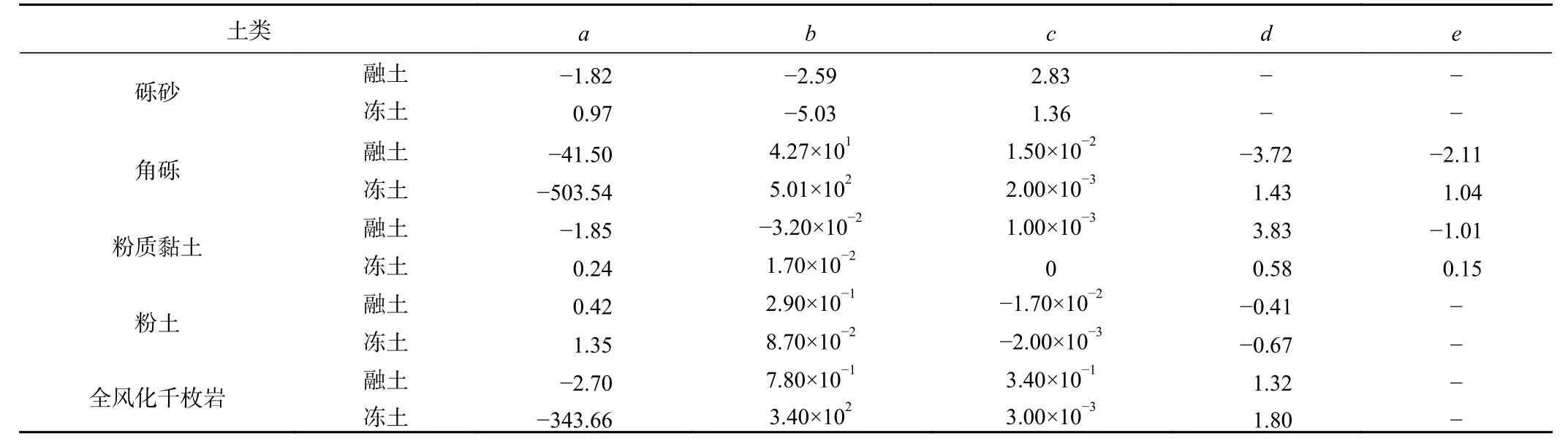
表5 各种土二元经验回归公式参数Table5 Binary empirical regression formula parameters for all kinds of soil
3.2 机器学习方法预测
机器学习以模拟人类学习方式并涵盖多种算法被广泛应用于各领域,具有广阔的发展前景。支持向量回归(Support Vector Regression,SVR)及径向基函数(Radial Basis Function,RBF)神经网络在处理小样本、非线性问题方面具有显著优势,故采用这两类方法进行以含水率和干密度为自变量、导热系数为因变量的二元回归预测对比分析。
SVR是以统计学习理论VC 维和结构风险最小化原则为理论基础的机器学习方法[25],通过核函数将低维问题转化到高维,进而找到最优超平面让所有数据距该平面总方差最小,实现回归目标。本文SVR 预测模型采用libsvm 工具箱在MATLAB 环境中实现,文献[26]证明采用RBF 核函数的SVM 必定线性可分,故核函数选用RBF 函数;惩罚参数(C)和核函数超参数(g)分别影响模型的泛化能力及运算速度,采用网格搜索和五折交叉验证进行寻优,具体参数见表6。

表6 SVR 预测模型网格搜索优选参数Table6 SVR optimal parameters obtained from grid search of the prediction model
RBF神经网络是种三层前馈型神经网络,具备局部逼近能力强及精度高的特点,通过隐含层的径向基函数将输入变量映射到高维空间实现线性可分[27],故本文利用MATLAB 神经网络工具箱中的newrb 设计函数构建预测模型。将各类土的冻融土导热系数测试结果按9∶1 随机分块,其中90%样本数据用于预测模型训练,剩余10%用作测试两类模型的预测能力。
五种土SVR 与RBF神经网络模型预测结果表明:这两种预测模型针对不同土性导热系数的预测效果呈差异性变化,其中SVR模型针对砾砂及粉土的预测效果要好于对应土性的RBF神经网络预测精度,相反剩余土类的RBF神经网络预测效果更佳,故两类方法的整体预测效果相近。对比冻融土导热系数预测结果,两种方法整体呈融土导热系数预测精确度略高于冻土的,其中角砾、粉土及全风化千枚岩融土导热系数预测结果的相关系数(R2)均大于0.85,具有很好的预测参考价值(表7)。
综合分析,对比三种预测模型下的各种土性及冻融土导热系数预测结果可得:全风化千枚岩预测效果最佳(图7),角砾、砾砂次之;粉土的SVR 及RBF神经网络效果较好,但经验公式拟合精度欠佳;粉质黏土则预测精度偏低,效果较差。这可能与采样山区对应土性组分含量差异大及热物参数分布离散性较大相关。三种方法下的融土导热系数预测效果整体略优于冻土的,其中SVR、RBF神经网络模型下角砾、粉土及全风化千枚岩融土导热系数预测精度较好,SVR模型下相关系数约0.9、相对误差10%以内的占比近90%,RBF神经网络模型下相关系数均大于0.9、相对误差10%以内的占比约95%左右。比较经验公式拟合、SVR 及RBF神经网络三种预测模型,通过对比相关系数(R2)、平均绝对百分比误差(MAPE)、均方误差(MSE)及相对误差10%以内的占比可得,两类机器学习模型预测效果要显著优于经验公式,且SVR与RBF神经网络预测性能整体相当,故形式简明的经验公式方法可满足部分土的一般工程估算要求,两类机器学习方法的应用土性范围更广,预测效果更佳。

图7 全风化千枚岩导热系数预测模型结果对比Fig.7 Comparison of the results of prediction models of thermal conductivity of fully weathered phyllite
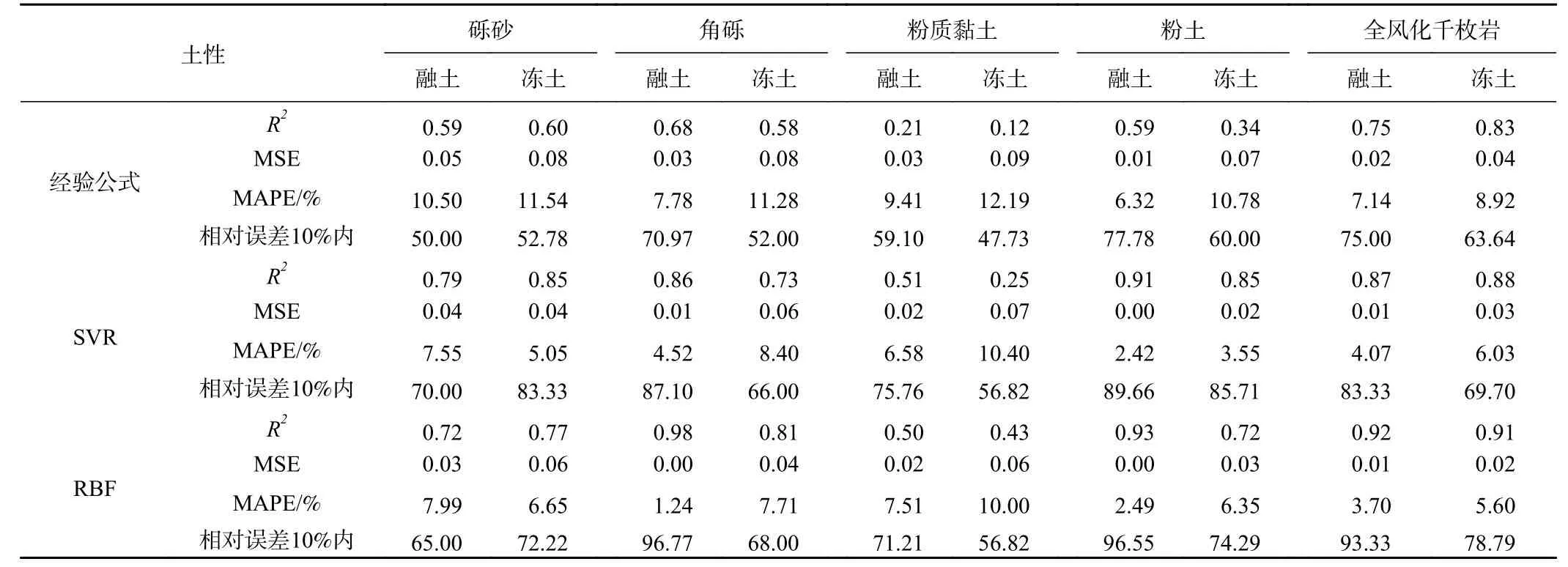
表7 经验公式与机器学习回归模型预测结果Table7 Forecast results of the empirical formula and regression model of machine learning
4 结论
(1)获取土样以黏土类、碎石土类和砂土类居多,导热系数测试结果呈现粗颗粒土大于细颗粒土特征,具体为冻土导热系数整体依砂土类、碎石土类、粉土类、全分化岩类和黏土类减小;融土导热系数整体依碎石土类、砂土类、粉土类、全风化岩类、黏土类减小。
(2)含水率和干密度对导热系数偏相关性分析表明,导热系数与二者均呈正相关性,不同土类相关性结果差异明显,典型土导热系数二元经验回归方程表现为非线性拟合结果。
(3)对比三种预测模型下的各种土性及冻融土导热系数预测结果可得,全风化千枚岩预测效果最佳,角砾、砾砂次之,粉土的SVR 及RBF神经网络效果较好,粉质黏土整体预测精度偏低;同时,融土导热系数预测效果整体略优于冻土。
(4)综合导热系数模型预测效果和误差结果可得,经验公式整体预测效果欠佳,可满足部分土的一般工程估算需要,SVR和RBF神经网络模型预测精度更高、应用土性范围更广。
