落石冲击混凝土板与缓冲层组合结构的动力响应

2021-01-21吴建利胡卸文梅雪峰许泽鹏

水文地质工程地质 2021年1期

吴建利，胡卸文,2，梅雪峰,3，许泽鹏，罗刚，韩玫

（1.西南交通大学地球科学与环境工程学院，四川成都 610031；2.西南交通大学，高速铁路运营安全空间信息技术国家地方联合工程实验室，四川成都 610031；3.山东理工大学建筑工程学院，山东淄博 255049；4.西南交通大学数学学院，四川成都 610031）

崩塌落石是高山峡谷区常发的边坡地质灾害之一[1]。针对高位（坡度大于25°，高差大于100 m）落石突发、高能的动力特性，棚洞及桩板拦石墙结构由于刚度大、防护性能好而被广泛应用[2-3]。典型的棚洞、桩板拦石墙通常由RC板及上覆、前置砂、碎石土缓冲层组成，可有效避免钢筋混凝土结构直接与落石接触发生刚性破坏。砂土或碎石土具有流、固两相性，作为一种多孔、松散、易压缩的颗粒材料，波在土体传播过程中表现出极强的弥散特性[4-5]，被广泛用于防护结构消能分配层。土颗粒受到冲击载荷时，即使颗粒密度非常高，也仅会发生冲压，不会发生广义的破坏。对于“合理”的结构，最大化消能层能量耗散及最小化混凝土结构吸能，能减小钢筋混凝土的损伤并增加结构的耐久性。一些学者研究了波在缓冲层介质内的传播规律。Calvetti[6]通过实验提出了土-结构相互作用机制及对冲击载荷扩散区域外土层的影响。Prisco[7]提出黏弹性本构模型，用于解释冲击波穿透土层过程。马炜[8]根据冲击速度，用相对密实、颗粒位错与滑移、颗粒射流三种形态描述砂土的流、固两相性。Seamen[9]采用落锤试验，研究了高岭土和黏土中应力波传播规律。于潇等[10]基于SHPB 装置研究了珊瑚砂应力衰减规律后，认为土颗粒级配决定了应力波衰减系数、峰值压力等。此外，最大冲击力及最大冲击深度是设计缓冲层厚度的重要参数。袁进科[11]基于室内模型试验，研究了落石重量、入射速度、缓冲层厚度等不同特征参量下的缓冲层表面冲击力变化规律。王星[12]、Ronco[13]、杨其新[14]、叶四桥[15]等学者分析了落石冲击过程中最大冲击力及冲击深度计算方法。Wang[16]通过能量原理推导了块状落石冲击土层时最大侵彻深度的计算方法。此外，路基设计规范[17]给出了一种计算弹坑最大深度的经验公式。关于落石防护结构的抗冲击方面的研究，Mougin 等[18]建立了1/3 钢筋混凝土板缩尺物理模型，研究了135 kJ冲击能量下板的动力响应并分析了板的破坏模式。Delhomme 等[19]采用数值模型对Mougin 等的试验结果进行了验证与分析。Zhao 等[20]基于模型试验研究了钢棚洞与砂土、EPE、EPS 不同组合形式的缓冲层在落石冲击作用下的缓冲效果。袁博[21]基于LS-DYNA有限元分析了川藏公路一处棚洞结构在落石荷载作用下的动力响应，并提出使用橡胶圈缓冲层以防止落石堆积的优化建议。

鉴于混凝土板与散体颗粒的复杂性，目前相关研究仍多见于单一材料分析，无法综合考虑组合结构的耦合影响，更多的学者采用数值模拟手段，缺乏更为可靠的试验验证。实际应用中，规范基于相关研究建议采用经验-半经验公式得到缓冲层表面的入射冲击力，通过应力扩散求得作用于下部防护结构的冲击压力，计算仅考虑冲击力的扩散忽略力的衰减，这会造成结构整体自重增大或占用更多的空间。基于以上问题，本文开展了物理模型试验，综合分析了缓冲层与RC板之间的相互作用，研究了冲击过程中峰值冲击力的衰减规律，揭示了RC板在不同冲击工况下的损伤累积与动态破坏模式。本文结果对落石防护结构的设计及优化具有指导意义。

1 试验方案设计

为研究上覆缓冲层的RC板结构在落石荷载下的动态响应及缓冲层耗能规律，开展了落锤冲击试验。考虑到传统室内小型落锤装置试验尺度受限问题，本文设计了用于开展上覆缓冲层RC板室外落石冲击试验平台（图1）。试验用RC板长2.4 m、宽1.6 m、厚0.25 m。混凝土采用42.5级硅酸盐水泥，粗骨料采用粒径为5～15 mm 连续级配的碎石，细骨料为天然河砂，板内垂直正交上下铺设2层φ14 @200 mm 钢筋网，混凝土保护层厚20 mm。实验所用的落石采用钢模内浇注混凝土而成，包括2种不同尺寸立方体块，编号C1、C2，边长分别为0.35 m和0.5 m，质量分别为107.3 kg和290.8 kg。在设计最大冲高7 m 下，对应的最大冲击能量分别为7.4 kJ和20.0 kJ。2种球体编号B1、B2，半径分别为0.15 m和0.2 m，质量分别为32.4 kg和70.7 kg，对应最大冲击能量分别为2.2 kJ和4.9 kJ。对试验用土颗粒缓冲层取样进行室内土工试验，相关的物理力学参数见表1，因在试验过程中未观察到明显的落石回弹，故回弹系数取零。RC板上下表面及板内钢筋网布置电阻式应变片，其中应变片布置方式上下层相同（图2）。混凝土板下表面中心点放置自复位式位移传感器，板上表面中心点布置1个动态压力传感器。试验采集指标主要包括落石冲击过程加速度、混凝土及钢筋应变、板竖向位移及板表面（缓冲层底面）压应力。为避免混凝土板提前破坏，需控制试验次序，按落石锤质量由小至大先进行B1、B2 及C1 在0.6 m 缓冲厚度下的试验工况。冲击高度从4 m 开始由小到大，按每1 m 递增至最大7 m。在以上试验完成后，缓冲层厚度减小0.1m，按照同样次序进行。当B1、B2 及C1 落石锤试验全部完毕后，采用C2 落石锤按照相同的试验次序进行测试。冲击试验工况及最大冲击能量见表2。每次试验前，需挖除比影响范围更大的土体重新回填压实并对数据采集仪清零，故所得结果仅为落石单次冲击的荷载效应。

图1 冲击试验平台Fig.1 Impact test set-up

表1 缓冲层参数Table1 Cushion parameters

图2 应变片布置(括号内数字为下表面应变片编号)Fig.2 Strain gauges (the number in parentheses is the bottom strain gauge)

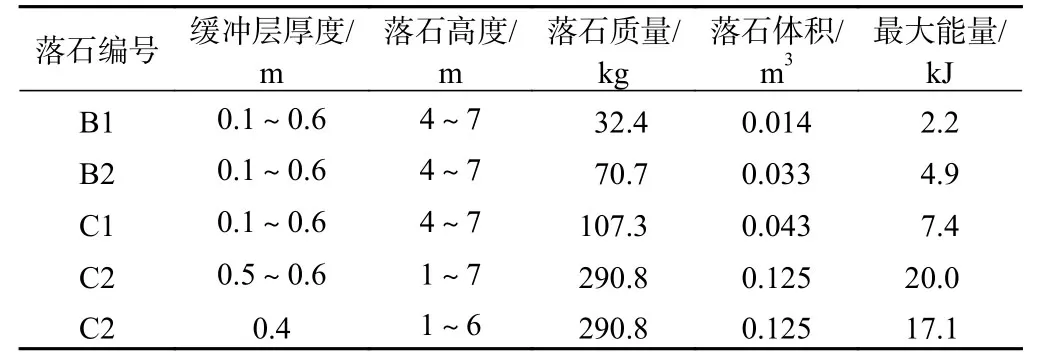
表2 试验冲击工况Table2 Conditions for each experiment

2 试验结果与分析

2.1 缓冲结构层受力分析

2.1.1 加速度分析

为方便分析，文中工况编号统一采用：落石锤编号-缓冲层厚度-冲击高度，如B2-0.1m-7m，代表B2 落锤-0.1m 厚缓冲层-7m 冲击高度，典型的加速度时程曲线如图3所示。加速度由初始值由零快速增大至峰值，该阶段为压缩加载阶段，随后加速度由峰值降至稳定，表征一次冲击过程完成。整个冲击历程持续时长约12 ms。根据牛顿定律，作用于缓冲层表面的峰值入射冲击力可由峰值加速度求得：

式中：F0-最大入射冲击力/N；

m-落石锤质量/kg；

a-落石锤加速度/（m·s-2）。

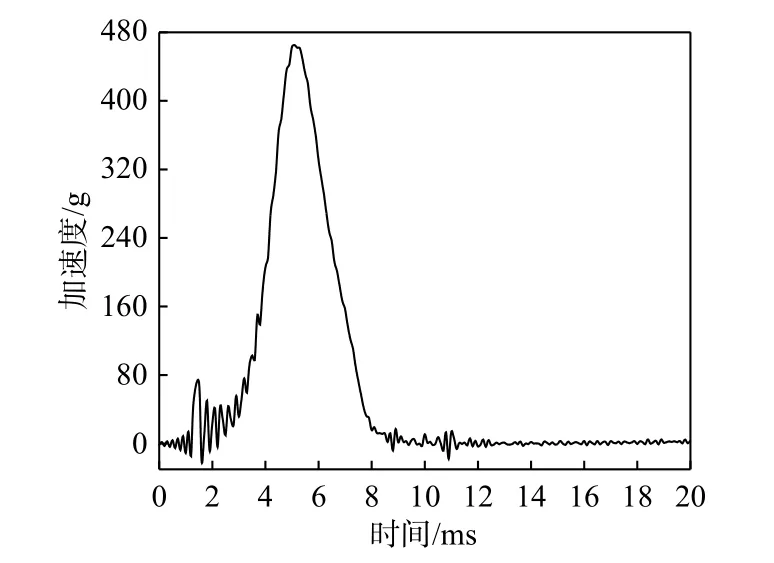
图3 B2-0.1m-7m工况加速度时程曲线Fig.3 Acceleration time history curve of the condition B2-0.1m-7m

目前一些关于冲击力计算公式通常认为缓冲层厚度对峰值冲击力无影响[22-23]。本文的实测数据表明（图4），随着缓冲层厚度的减小，峰值加速度与缓冲层厚度服从指数函数关系。当缓冲层厚度为0.6 m，0.5 m和0.4 m时，峰值加速度随缓冲层厚度的减小增大的趋势较平缓，在缓冲层厚度减小至0.2 m和0.1 m时，峰值加速度随缓冲层厚度减小而迅速增大，其中在相同冲击高度下0.1 m 缓冲层厚度对应的峰值加速度比0.2 m时大2～4倍。因此，不考虑缓冲层厚度的冲击力计算公式可能会导致计算结果失效。

2.1.2 弹坑深度与冲击力关系分析

落石冲击过程中穿透缓冲层的最大深度通常被用作缓冲层厚度的最小设计值。本文在试验过程中测得冲击深度的最大值。由于多数研究冲击深度的计算方法仅适用于球状落石，为方便与前人的研究成果进行对比分析，本文仅统计了球状落石锤的相关数据。根据实测结果，在Ronco[13]基础上提出了最大冲击深度的计算方法：

式中：δ-弹坑最大冲击深度/m；

m-落石质量/kg；

v0-冲击接触时最大的速度；

H-冲击高度/m；

g-重力加速度，取9.81 m/s2；

F0-峰值入射冲击力/N。

由式（2）可知，弹坑的最大冲击深度与落石冲击速度（高度）及最大冲击力有关。实际工程应用中，速度与冲击力是最基本的2个特征量，通过式（2）即可计算出落石的最大冲击深度，从而进一步进行缓冲层厚度的设计。将其他学者的计算结果与本试验实测数据及本文公式计算结果进行对比分析，结果见图5。其中x轴是试验过程中实测数据，y轴为王星等[12]、路基规范法[17]及本文公式计算值，计算所需的参数见表1。结果表明，3种计算结果趋势一致，路基规范法计算的结果均大于实测值。王星等模型和本文建议的方法与试验所测数据吻合度最优。但路基规范法要考虑缓冲层的内摩擦角及落石重度等参数，而王星等的计算公式要考虑恢复系数等。本文方法只需考虑最大冲击力及冲击速度两个基本特征参量，可避开复杂参数选取，作为缓冲层最小厚度设计依据是科学的。

2.1.3 冲击力衰减规律分析

通常由于上部缓冲层的消能作用，入射冲击力F0穿透缓冲层至下部RC板的透射冲击力合力F1已大大减小（图6）。根据Ronco 等[13]的数值模拟研究结果表明，冲击力以压缩波的形式从冲击点开始呈锥形向墙体后方传播，土体在被压缩的过程中，80%～85%动能通过土体击实的方式塑性耗散。F1的大小

图4 峰值加速度与缓冲层厚度关系Fig.4 Relationship between the peak acceleration and thickness of the cushion layer

图5 冲击深度试验值与规范及其他方法对比Fig.5 Comparison of the tests and the calculations at different methods with those of the national standards and the other

由影响区内透射力积分得到：

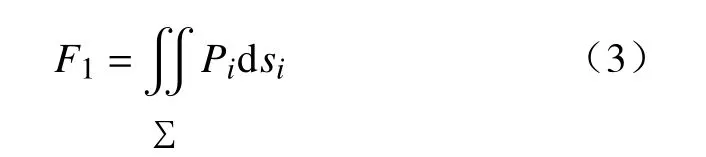
式中：F1-作用于混凝土板上表面透射冲击力合力/N；

Pi-影响范围内测点压力荷载值/Pa；

dsi-微单元面积/m2。

图6 冲击力的扩散和分布特性Fig.6 Diffusion and distribution characteristics of the impact force

落石在冲击过程中，入射冲击波以一定的角度向缓冲层深部扩散称为扩散角。目前隧道设计规范中[24]给出了扩散角的具体数值，一般来说扩散角与缓冲层性质有关，根据与本试验相关土体的性质，本文采用的扩散角及扩散半径[25]为：

式中：θ-缓冲层扩散角/（°），与缓冲层性质有关；

φ-土体内摩擦角/（°）；

L-影响区半径/m；

r-落石的等效半径/m；

h-缓冲层厚度/m。

图7为位于RC板上表面中心点位置的力传感器在不同冲击工况下的透射力时程曲线。峰值透射力与冲击高度及冲击质量正相关。相对于落石加速度时程曲线，透射冲击力由零增加到最大值几乎无滞后，在整个冲击时长20～30 ms时间内可视为1个脉冲荷载。随缓冲层厚度增大，曲线末期存在明显缓降平台，随后逐渐趋于零。

图7 不同冲击高度透射力时程曲线Fig.7 Transmission time history curve at different falling heights

图8为C1、B1、B2 落锤在冲击高度分别为4，5，6，7 m 对应不同厚度缓冲层下的衰减规律。结果表明，无量纲峰值冲击力与缓冲层厚度关系符合指数函数。随缓冲层厚度的减小，无量纲峰值冲击力 η 增大，入射冲击力衰减程度越来越小。如C1 落锤在0.3 m厚缓冲层最大入射力衰减了约47%，当缓冲层增大至0.6 m时，入射力衰减了约73%，这证明缓冲层的耗能效果明显。与B1、B2 相比，相同工况下平底落石C1的衰减效应稍强，这可能是由于平底接触面的冲击力更分散导致的。此外，随着缓冲层厚度不断增大衰减值趋于平缓，也即缓冲层厚度的衰减效应越来越弱。以C1 落锤为例，根据衰减趋势，当缓冲层厚度增加到1.5 m

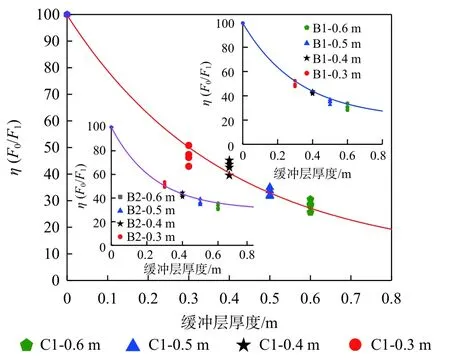
图8 缓冲层厚度与无量纲峰值冲击力间的关系Fig.8 Relationship between the cushion layer thickness and dimensionless impact force

目前关于透射冲击力的分布形式，得到的结果主要有指数分布[7,26]及线性分布[14,27]。为简化计算过程，本文采用线性分布规律进行分析。选取典型的不同冲击工况下透射力时程曲线，并定义无量纲峰值冲击力η为：时，最大入射力衰减率大于90%，但是过大的缓冲层厚度显然是不经济的。因此通过本文的衰减规律可以评估缓冲层厚度增加对入射冲击力衰减的影响程度。进一步对无量纲峰值冲击力与缓冲层厚度h的关系拟合。采用麦考特（Levenberg-Marquardt）算法拟合为指数函数，拟合函数的相关系数均大于0.95，证明拟合效果较优，具体表达式为：

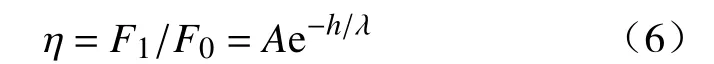
式中：A-缓冲层材料参数，与土体的密实度及颗粒级配等相关；

λ-与落石尺寸有关的参数；

h-缓冲层厚度/m。

对于本文所涉及的缓冲层拟合值A=0.990，对于B1 落石锤λ=0.498 m-1，B2 落石锤λ=0.475 m-1，C1 落石锤λ=0.456 m-1。可以看出落石锤尺寸越大，对应λ越小。实际应用中，可以根据具体所使用缓冲层土体进行试验确定。

2.2 RC板结构动态响应

2.2.1 混凝土板位移特征分析

选取冲击过程中RC板下表面中心点典型的位移时程曲线见图9。结果表明，RC板位移特征基本可分为2个阶段：（1）板跨中挠度由零迅速增加至峰值。（2）以峰值为界，RC板发生回弹，跨中挠度迅速减小，在冲击能量较大的情况下RC板会产生一定的残余变形。

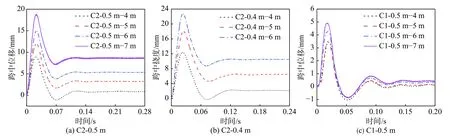
图9 混凝土板跨中位移特征Fig.9 Central deflection characteristics of RC slab

图9表明，冲击能量对RC板的变形具有关键作用。对于B1，B2 落石锤，无论何总冲击高度，RC板基本处于弹性工作状态不产生塑性变形。此外，在0.5 m缓冲层厚度下，C2 产生的峰值位移及残余变形远大于C1。相同落锤及冲击高度下，较大缓冲层厚度能有效减小残余变形，缓冲层消能效果明显。C2 落石在缓冲层厚度为0.5 m和0.4 m、高度4～6 m工况下，残余变形分别为0.862，3.23，5.36，2.367，6.74，10.53 mm。缓冲层减小0.1 cm，4～6 m工况下残余变形分别增加174%、108%、96%。

表3汇总了4组典型的试验数据。对比C1与B2分别在缓冲层厚度0.3 m和0.5 m时的冲击试验数据发现，虽然质量更大的C1 入射冲击力远大于B2，但由于缓冲层厚度的差别使得两者透射力差距较小，表现为钢筋及混凝土各测点应变值及RC板中心点的最大位移基本一致。以混凝土中心点S8 测点为例，在冲击高度为5～7 m时，C1-0.5 m 冲击工况下对应的应变值分别为102.3，126.9，164.0 με，而B2-0.3 m 冲击工况下的应变值分别为112.2，126.1，147.6 με。因此本文衰减理论能够合理反映不同冲击工况下冲击力衰减情况。。

图10为C2 落锤在0.5 m 厚度缓冲层-7 m 冲击高度工况下的应变及位移变化曲线，由于数据采集于混凝土破坏末期，钢筋及混凝土各测点应变值普遍增大，其中跨中测点S8 及S11 迅速增大，除由于RC板吸收的能量较大外，可能也与前期累积能量使得混凝土屈服有关。具体表现为产生大量不可逆应变及塑性位移，应变回弹很小，峰值应变约等于塑性应变。

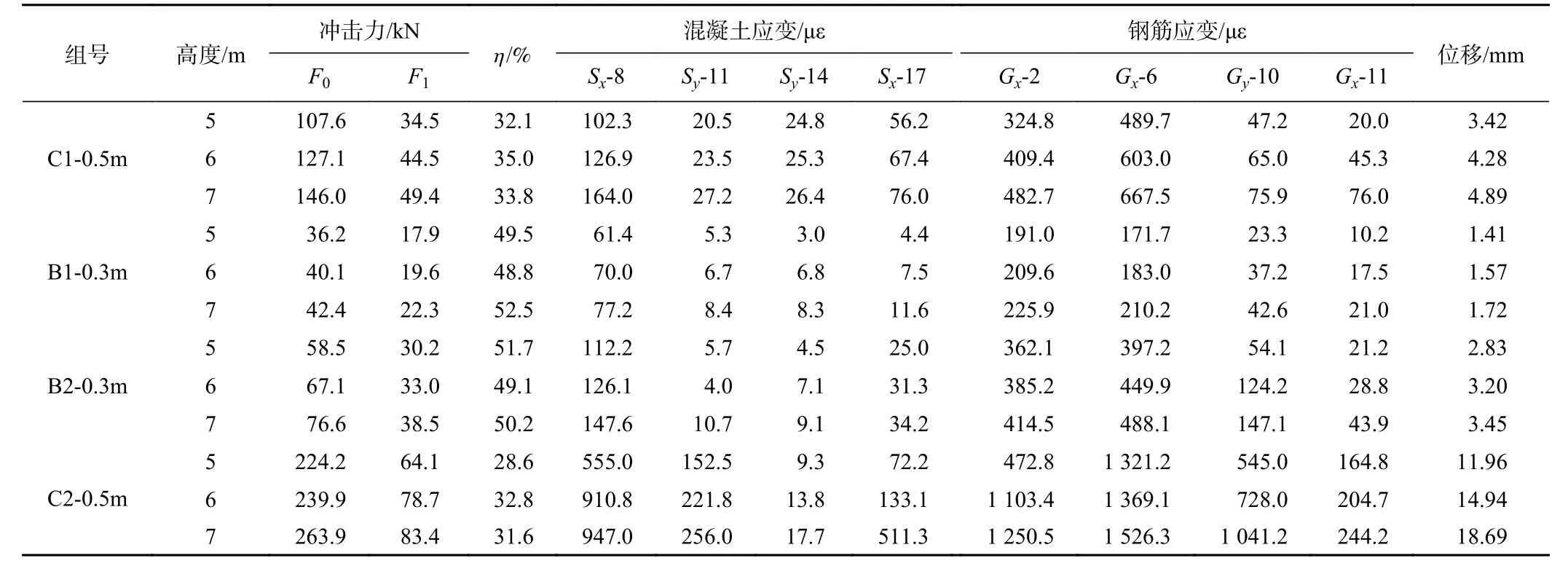
表3 典型试验数据Table3 Typical tests data

图10 C2-0.5m-7m 作用下RC板位移及应变Fig.10 RC slab deflection and strain under C2-0.5m-7m

2.2.2 钢筋混凝土板破坏特征

冲击过程中，初始输入总能量为不同高度所对应的重力势能。其中一部分能量被缓冲层耗散，另一部分被RC板吸收。对透射力-位移曲线进行积分可得到透射力对RC板所做的功。图11为C1 落石锤在缓冲层厚度为0.3 m、冲击高度分别为4，5，6，7 m 冲击工况下的透射力-位移曲线。结果表明，透射力可视为脉冲荷载瞬时作用于RC板。曲线围成的面积即为透射力对RC板所做的功。随冲击高度的增加，透射力-位移曲线所围面积明显增大。当位移达到最大值时，RC板发生回弹并在震荡中趋于零，说明未产生塑性变形。

图11 冲击荷载下透射力-位移曲线Fig.11 Relationship between the impact loading and displacement

图12汇总了冲击过程中的输入总能量以及透射冲击力对RC板所做的功。整个试验产生了约588 kJ能量，由于缓冲层的缓冲消能作用，约82%的能量被缓冲层吸收。其中在C1 与C2 落石锤的冲击工况中，RC板累计吸收的能量为82.7 kJ，占RC板吸收总能量的80%。

图12 能量分配比例Fig.12 Energy distribution ratio

图13 RC板破坏冲击作用下变形破坏过程Fig.13 RC slab failure process

图13选取了冲击过程中RC板不同时刻对应的典型破坏照片。分析随累积撞击能级逐渐增大，RC板裂纹的形成与扩展过程：（I）弯曲起裂及扩展（图13a）。初始变形由RC板跨中底部产生弯曲裂纹Crack 1 开始。随着输入能量的增大，裂缝竖直向上延伸至20 cm，但宽度小于1 mm。由于落石锤质量小，单次冲击能量较小，因此产生的损伤最小，RC板处于带裂缝弹性工作状态。至主裂缝向上扩展至20 cm的过程内，累积输入能量约157 kJ，RC板吸收能量约22 kJ。(II)次级弯曲裂纹的产生与扩展（图13b）。在随缓冲层厚度减小、累积能量增加的情况下，跨中弯曲主裂纹基本贯通至顶部，两侧开始产生新的次级弯曲裂纹，如图13（b）中的Crack 2、Crack 3。与（I）相比，跨中主裂纹宽度急剧变大，由开始的0.8 mm 增大至12 mm。RC板吸收的能量主要贡献于跨中弯曲裂纹变宽及次级弯曲裂纹产生，RC板发生明显的塑性变形。弯曲破坏仍为主要变形模式。此过程累积输入能量约116 kJ，RC板吸收的能量约34 kJ。（III）剪裂纹产生及弯曲裂纹贯通（图13c）。在C2 落石锤冲击缓冲厚度分别为0.6 m 及0.5 m工况下，随缓冲层厚度减小，累积能量增大，裂纹Crack1 宽度进一步加剧，跨中两侧开始产生明显的剪切斜裂纹及旁侧羽状随机裂纹，RC板兼有弯曲与剪切变形特征，RC板下表面混凝土发生崩落。对应输入能量约190 kJ，RC板吸收的能量约31 kJ。（Ⅳ）试验末期。在C2 落石锤冲击缓冲层厚度为0.4m 试验工况下中，Crack 1 宽度无明显增加，产生明显斜剪切裂纹（图13d），周围羽状随机裂纹加密变宽，弯曲裂纹与剪切裂纹连通。整体上RC板沿y向在跨中“折断”。RC板既具有弯曲破坏的转动特征，又兼具剪切破坏的错动特征。该过程对应累积冲击能量约60 kJ，混凝土板吸收能量约18 kJ。图13（e）、图13（f）为RC板上下表面最终形态，其中板上表面由于压应力而压溃，压溃范围对称分布于跨中轴线40 cm 范围内，可观察到大量的混凝土剥落碎屑。压溃范围以外，表面形态完整，但存在明显的残余变形，离中轴线越远残余变形越小。RC板下表面产生纵向贯通的宽大拉裂缝。混凝土崩落形成震塌坑。板下表面分布多条与纵向裂缝垂直的横向裂缝，但裂缝宽度与延伸程度远不及跨中纵向裂缝。