基于速率的Allan 方差的GPS 坐标时间序列噪声特性分析

2021-01-21高启平

科学技术创新 2021年2期

高启平

（甘肃省地图院，甘肃兰州730000）

1 概述

GPS 基准站坐标时间序列中的噪声之间是相关的[1]，忽略声之间的相关性会影响GPS 基准站速率的不确定性，因此，对GPS 基准站坐标时间序列进行噪声特性分析至关重要。二十年来，不同学者针对GPS 基准站坐标时间序列的噪声特性采用了多种的方法进行分析，国内外学者Zhang、Langbein、William、Bos、田云峰、袁林果、李昭、贺小星等分别采用最大似然估计（Maximum Likelihood Estimator，MLE）对不同区域的GPS 基准站坐标时间序列进行噪声分析[2-9]，黄立人[10]采用谱分析方法分析了中国地壳运动观测网络GPS 基准站时间序列相关的噪声特性，Hackl[11]采用基于速率的Allan 方差对GPS 基准站坐标时间序列的噪声特性分析。MLE 方法估计的结果比较稳健，但其计算效率较低；功率谱分析方法计算速度较MLE 方法快，但功率谱分析方法需要数据等间隔的，但实际数据一般不能满足，尤其数据有大量缺失时。基于速率的Allan 方差方法具有方法计算速度快，效率高，尤其是对于GPS 坐标时间序列数据有大量缺失，其噪声特性计算结果仍较为稳健。基于此，本文采用采用基于速率的Allan 方差方法分析了GPS 基准站坐标时间序列的噪声特性，并与MLE 方法分析的结果进行了对比。

2 原理方法

Allan 方差是David Allan 于1966 年提出的，最初该方法用于分析精密振荡器的相位和频率稳定性，由于陀螺等惯性传感器本身也具有振荡器的特征，因此该方法随后被广泛应用于各种惯性传感器的噪声特性，Allan 方差已成为时域的噪声分析标准工具。

Allan 方差的基本原理：假定数据长度为N 的坐标序列X（i），i=1、2…N，采样间隔为T，将该坐标序列分成n 组，一般来说n＞4，分别求出每组数据的平均值m（i），i=1，2，…n，则Allan 方差的表达式为：

本文参考文献[11]的算法，Allan 方差在每组数据中均值m（i）由该段数据拟合直线的速率代替，因此Allan 方差的计算结果不会因为数据缺失而剧烈的变化，且是否去趋势项对计算的结果影响也较小。

对于给定的谱指数k 与长度t 的位置时间序列，Agnew 分析了时域里的幂律过程[12]，推导出了其与标准差σx的关系如下：

因此，基于速率的Allan 方差σ2与谱指数k 的关系如下：

在双对数坐标系中谱指数k 和与基于速率的Allan 方差的关系为：

即μ 和MLE 估计谱指数k 之间的关系与对应的噪声类型是一致的，如表1 所示。

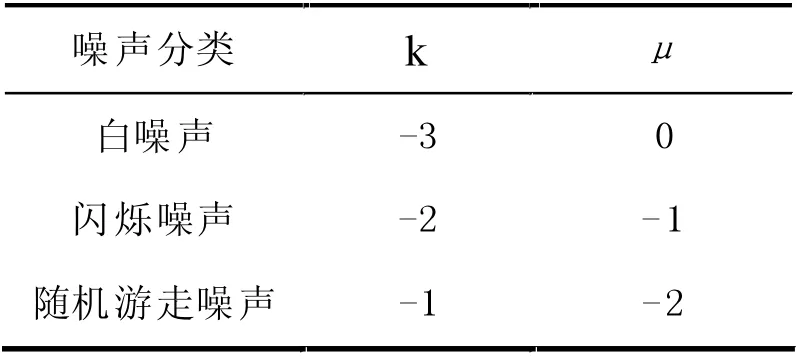
表1 两种方法谱指数之间的关系

3 实测数据处理

选用6 个GPS 基准站N，E，U 三个方向坐标时间序列分别采用基于速率的Allan 方差与MLE 方法进行噪声特性分析。两种方法计算的结果如表2 所示。

从表2 中可以看出，经公式（4）转换后，基于速率的Allan方差方法得到的谱指数与MLE 估计得到的谱指数基本上是一致的，证明了基于速率的Allan 方差方法估计谱指数的有效性，GPS 基准站坐标序列主要表现PL+WN 噪声模型特性，GPS 测站时间序列不同方向之间的噪声特性不尽相同。

为验证GPS 基准站坐标时间序列数据缺失对基于速率的Allan 方差的影响，对RTUC 站的坐标时间序列时分别随机删除100、200、300、400、500、1000 个数据，然后在采用基于速率的Allan 方差估计其谱指数，并与原始数据计算结果进行对比，如表3 所示。

表2 两种方法计算得到的谱指数

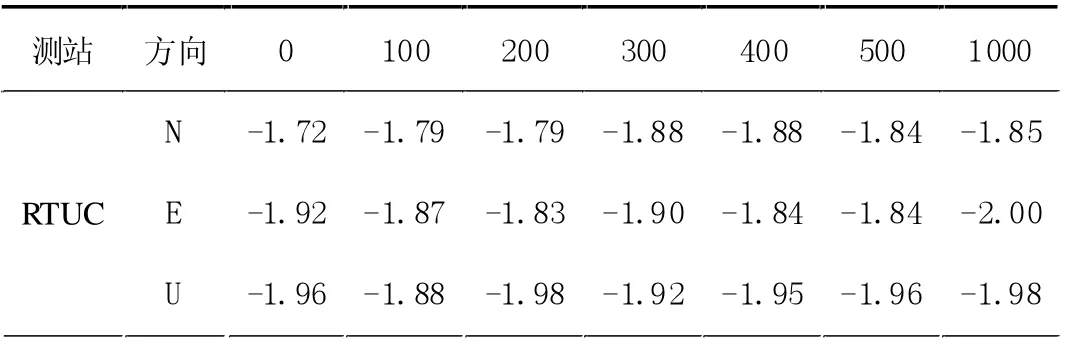
表3 随机删除不同数量数据后的谱指数计算结果

从表3 可知，RTUC 站坐标时间序列随机删除不同数量数据后，采用基于速率的Allan 方差估计得到的谱指数保持着相对稳定得结果。经多次重复计算，相邻两次结果保持了高度一致性。

当数据出现缺口时，为了验证基于速率的Allan 方差在数据出现间断时，其估计结果仍较稳定，将RTUC 站坐标时间序列数据在任意位置随机删除100、200、300、400、500、1000 个连续数据，然后计算其谱指数，并与原始数据计算结果进行对比，如表4 所示。

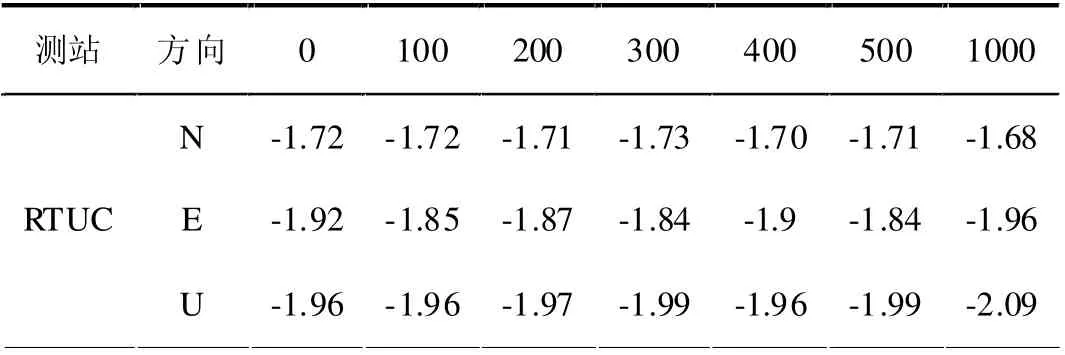
表4 随机删除连续数据后的谱指数计算结果

从表4 可知，RTUC 站坐标时间序列随机删除不同数量的连续数据后，采用基于速率的Allan 方差估计得到的谱指数保持着相对稳定得结果，仅在U 方向上，连续缺失1000 个数据后，其谱指数相对变化较大。综合表3 及表4，可以看出，数据缺失对基于速率的Allan 方差方法估计谱指数影响较小，证明了该方法的优越性。