硅胶- 水吸附式制冷系统吸附床结构优化研究

胡伟 赵越

（1、济南市生态环境局历城分局，山东 济南250100 2、山东大学能源与动力工程学院，山东 济南250061）

随着社会的不断发展以及人类生活品质的提高，对于制冷的需求量也将不断增加。传统的蒸汽压缩制冷技术大多采用非环保型制冷剂，对大气中臭氧层破坏严重，给人类及生态环境造成损害。吸附式制冷技术以其无任何污染、可利用低品位热源驱动的优点成为了蒸汽压缩式制冷技术的潜在可代替方案。但是吸附式制冷技术发展还不够成熟，吸附剂传热性能差、循环吸附量小以及吸附床内部传质过程缓慢导致吸附式制冷机组占地面积大、COP/SCP 值不高，这些显著缺点制约其商用化进程。

为了强化吸附床内部的换热过程，国内外学者从三方面展开工作。一方面是改善吸附剂传热性能，将吸附剂固化处理；另一方面是采用涂层吸附床，减小吸附剂与金属壁面的接触热阻；还有一方面是对吸附床结构的优化设计，增加金属与吸附剂之间的换热面积[1]。

吸附床结构优化的主要研究内容包括：通过实验或者数值模拟方法探究不同参数（如：翅片类型、翅片间距、翅片高度、翅片厚度等）对系统性能影响，从而得到优化的吸附床设计方案。通过实验方法获取吸附床的优化设计方案势必耗费大量人力物力资源，具有一定局限性；通过数值模拟方法获取吸附床的优化设计方案较为简单快捷，可以对实验验证起到指引作用。很多学者已经对吸附床的工作过程进行数值模拟研究，他们所采用的数学模型也不尽相同，表1 是对他们所采用数学模型的总结[2-11]。

表1 现有吸附式制冷/热泵数值模拟研究模型总结

本文目的是通过数值模拟方法优化管翅式吸附床尺寸参数及循环时间，建模过程考虑吸附剂、吸附床内部的传质阻力，采用局部热平衡法（LTE）定义能量守恒方程，数学模型可以较为准确的反映硅胶- 水管翅式吸附床瞬态吸附过程。本研究的创新点是考虑吸附过程中吸附剂颗粒与吸附床金属部分接触热阻的变化，以及对各因素影响程度的计算。

1 物理模型

本文所采用的硅胶- 水工质对管翅式吸附床物理模型示意图如图1 所示，吸附剂填充在翅片与铜管之间，32℃以及85℃的冷/热水在铜管中交替流动，用于制冷剂的吸附/解吸过程，吸附/解吸过程发生时，制冷剂气体从吸附床的外表面流入/流出。本研究物理模型的尺寸参数列于表2。为了简化计算，加快求解过程，且由于吸附床模型的对称性，本研究计算域采用二维吸附床模型中的一部分，如图2 所示：

图1 翅片管式吸附床剖面结构示意图

图2 本研究采用的二维吸附床物理模型

表2 模型参数

2 数学模型

硅胶的吸附过程较为复杂，在进行数学模型构建以前需要做如下假设：

（1）硅胶颗粒粒径一致，吸附床空隙分布均匀。

（2）硅胶在吸附过程中其物性参数恒定不变，且各向同性。

（3）水蒸气被吸附后其热力学性质可视为液态水。

（4）吸附床与外界环境不发生热交换。

（5）铜管与铝翅片之间无接触热阻。

（6）制冷剂气体可视为理想气体。

2.1 质量守恒方程

吸附剂层质量守恒方程：

吸附剂层质量守恒方程包括三项，其中第一项为制冷剂气体流入/流出吸附剂层引起的质量变化；第二项为吸附床床层空隙之间的制冷剂蒸汽质量变化项；第三项为吸附/解吸过程发生时吸附/解吸制冷剂气体质量变化项。方程式为（1）：

其中：ρg代表制冷剂气体的密度，kg/m3；u 代表制冷剂气体的流速，m/s；εb代表吸附床的床层空隙率，ρs代表硅胶的真实密度，kg/m3；εt代表吸附床的总孔隙率，x 代表吸附量，kgw/kgs。

吸附床总孔隙率的计算式如方程（2）：

其中：εs为硅胶的孔隙率。

2.2 动量守恒方程

制冷剂气体动量守恒方程：

本研究采用非均匀压力场模型，吸附床内部的压力梯度致使传质效应变缓，阻碍吸附/解吸过程进行。

常用于描述制冷剂气体在吸附剂颗粒之间运动的动量方程有Darcy 方程，为（3）。

其中，k 代表吸附床渗透率，m2。对于孔隙率小于0.5 的吸附剂填充床，吸附床渗透率可由Blake-Kozeny 半经验方程（4）

其中，dp代表吸附剂粒径，mm。

根据理想气体状态方程可计算气体压力：

2.3 能量守恒方程

2.3.1 金属层能量守恒方程

将铜管与铝翅片视为吸附床的金属层，金属层发生的能量交换包括铜管与吸附剂的换热以及与冷/热水的对流换热、铝翅片与吸附剂层的换热，具体形式为（6）。式中第一项为铜管内能变化项，第二项为铝翅片内能变化量，第三项为铜管与吸附剂的换热项，第四项为铝翅片与吸附剂的换热项，第五项为铜管与冷/热水的对流换热项。

其中：ρtube代表铜管的密度，kg/m3；Cp，tube代表铜管的定压热容，J/（kg*K）；ρfin、Cp，fin、Tfin分别代表铝翅片的密度、定压热容、温度，htube，s代表铜管与吸附剂层的换热系数，W/（m2*K）；hfin，s代表铝翅片与硅胶的换热系数，W/（m2*K）；htube，water代表冷/热水与铜管的对流换热系数，W/（m2*K）；Ts代表硅胶温度，K。Hamid Niazmand[10]的研究考虑沸石吸附过程中与吸附床金属层接触热阻的变化，本研究采用同样的计算方法：

冷/热水与铜管的换热系数采用如下公式计算：

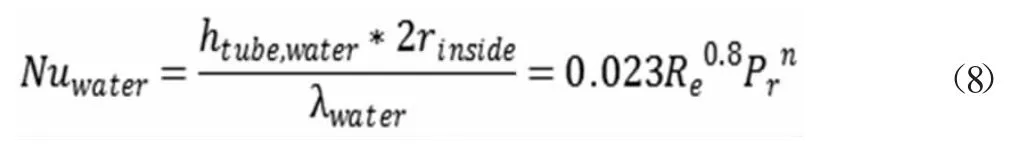
λwater代表冷/热水的导热系数，W/（m*K）；当通冷却水时，n取0.3，当通热水时，n 取0.4。

2.3.2 硅胶吸附剂层能量守恒方程

硅胶吸附剂层包括硅胶吸附剂、空隙中的制冷剂气体以及吸附的液态制冷剂。Ismail Solmus[13]采用局部热非平衡法（LTNE）研究硅胶吸附过程能量变化，发现吸附初始阶段制冷剂气体与吸附剂温差大于4℃，经过50s，温差小于4℃，验证了局部热平衡（LTE）假设的合理性。考虑到制冷剂气体与吸附剂之间换热量很少，以及为了模型的简化，本文采用局部热平衡法分析吸附剂层的能量变化，认为局部吸附剂温度与制冷剂温度一致，不考虑制冷剂气体与吸附剂之间对流换热。那么吸附剂层的能量守恒方程可以写作（9）：

式中，ρCp，eff代表吸附剂层的等效热容，J/（m3*K）；Cp，g代表制冷剂气体的定压热容，ΔHads代表吸附热，kJ/kg。吸附剂层等效热容计算公式如下：

Cp，s代表硅胶吸附剂的定压热容，J/（kg*K）。硅胶吸附水时其热容是一个随吸附量不断变化的函数，因为硅胶吸附的水蒸气其性质近似视为液态水，硅胶热容可由（11）描述：

Cp，s，0代表未进行吸附时的硅胶热容，Cp，w代表液态水的定压热容。

2.4 硅胶- 水吸附动力学及平衡态方程

硅胶的吸附过程是一个动态过程，常用于描述硅胶- 水吸附工质对的吸附动力学模型有线性驱动力（LDF）模型、固体扩散（SD）模型。这两种模型均考虑了吸附/解吸过程进行时制冷剂气体在吸附剂颗粒孔内扩散过程，传质阻力导致吸附/解吸过程无法立即达到平衡状态。

因LDF 模型便于求解，且可以准确的描述非平衡吸附过程[14]，成文本文的选择目标，方程如下：

Ds为参考扩散系数，rp为硅胶颗粒的半径，x*代表平衡吸附量，x 代表当前吸附量。

常用于描述硅胶- 水工质对吸附平衡态方程有：Henry 定律、D-A 方程、Freundlich 方程、Toth 方程。本文采用Wang[2，15]提出的Toth 方程：

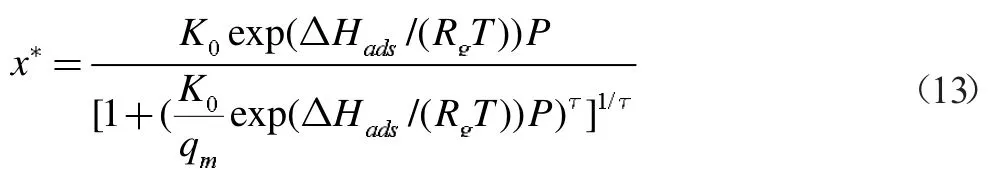
2.5 性能系数计算方法

本研究COP、SCP 的计算式如下：

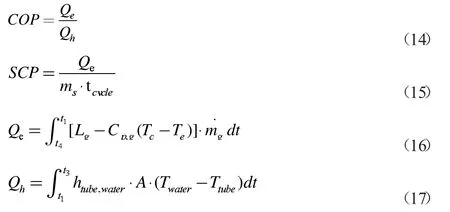
表4 本研究所采用的初始/边界条件

t1→t2代表定容升温过程时间，s；t2→t3代表定压解吸过程时间，s，ms代表填充硅胶质量，Lg代表蒸发温度时制冷剂的汽化潜热，Tc、Te分别代表冷凝温度和蒸发温度，m˙g 代表吸附/解吸过程中制冷剂气体的质量流量，A 代表冷/热水与管壁的接触面积，Twater代表冷/热水温度，经Skander Jribi[16]实验研究，冷/热水进出口温差变化较小，本研究将冷/热水温度视为恒定值。

本研究所采用的模拟参数总结于表3。

2.6 初始条件及边界条件

本研究所采用的的初始条件及边界条件列于表4。

3 正交实验设计

本研究的正交实验设计考虑四个主要影响吸附床性能参数的因素（循环周期、翅片高度、翅片间距、翅片厚度），其中每个因素各取四个水平，如表5 所示，设计L16（45）正交实验表。

本研究同样利用方差分析法对正交实验结果进行分析，探究四因素对SCP、COP 的贡献水平，并筛选出最优设计方案。

本研究利用有限元法求解以上偏微分方程组，在进行网格无关性验证后，利用约6000 个非结构化网格将初始计算域离散，边界层手动加密，通过子域的近似解推导整个求解域的近似解，使用变时间步长求解器，采用向后差分公式（BDF）计算时间步长，根据以上方法求解得到所需物理量。

表5 L16（45）正交实验表

4 结果分析

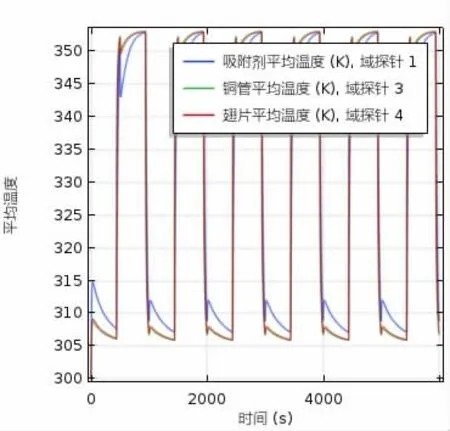
图3 平均温度随时间变化规律

本章节对所研究内容结果进行总结，每一种模型计算多组完整循环过程，使吸附循环达到稳定状态（最终两次循环最大吸附量差值小于0.001kgw/kgs），并选用最后一个循环中参数进行COP、SCP 计算，用来消除初始条件对研究结果的影响，模拟结果如下：

4.1 模型参数随时间变化规律

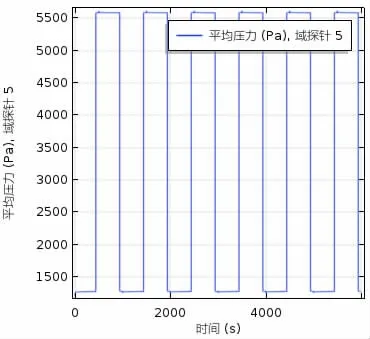
图4 平均压力随时间变化规律

图5 平均吸附量随时间变化规律

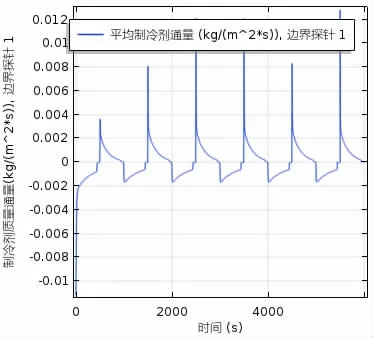
图6 制冷剂气体质量流量随时间变化规律

图3-6 分别代表多个循环进行时模型参数的变化规律，通过与既有研究比对分析[4，10，16，17，18]，发现本研究参数变化规律与参考文献有较好的一致性，证明了本研究数学模型的正确性。

4.2 正交实验结果分析

利用方差分析法对表5 中实验数据进行处理，得出结论如图7、8。

利用显著性水平5%对正交实验数据进行检验。由图7 可以看出，翅片间距、循环周期对SCP 的影响均显著，翅片高度的影响接近显著，翅片厚度对SCP 的影响不显著；仅有循环周期对COP 的影响显著，翅片厚度对COP 的影响接近显著，翅片高度及翅片间距对COP 的影响较小。计算各因素各水平SCP、COP之和，用来确定最优组合，如表6 所示。

根据表6 可以得出：当循环周期为1000s，翅片高度、翅片间距、翅片厚度分别为10mm、2mm、0.64mm 时，为SCP 最优化的设计方案。翅片高度、翅片间距较小，翅片厚度较大时，吸附床金属体积相对占比较大，传热效果较强，有利于提高SCP；循环周期为1000s 时，虽然吸附剂的循环吸附量较小，但是由于吸附/解吸过程反应速率随时间逐渐减缓，综合两者，SCP 随着循环周期的增加而减小，这也与以往研究结论相同[8，10，16，19]。根据得出的最优方案进行仿真计算，求解得出SCP 值为120.09W/kg，此时COP 为0.43554。

根据表7 可以得出：当循环周期为1600s，翅片高度、翅片间距、翅片厚度分别为10mm、2.4mm、0.4mm 时，为COP 最优化的设计方案。其原因是：翅片厚度的增加引起金属占比的增加，在切换过程中供给金属翅片的能耗增加，翅片厚度的减小有利于COP 提升；同样翅片高度以及翅片间距的增加也会引起金属耗能的增加，但是随着翅片高度以及翅片间距的增加，吸附剂占比也同样增加，由于这两点原因，翅片高度、间距分别为10mm、2.4mm 时，COP 最优；循环周期为1600s 时，吸附/解吸过程也进行的更为充分，在进行解吸过程时，随着时间的进行吸附床金属温度越接近供给热水温度，两者之间传热速率逐渐减缓，供给热量主要用于吸附剂的升温以及制冷剂的解吸吸热，因此COP 随循环周期的增加而增加。关于COP 的研究结果也与Hong[8]的研究结果一致。根据得出的最优设计方案进行仿真计算，求解得出COP 值为0.51185，此时SCP 值为87.24W/kg。

5 结论

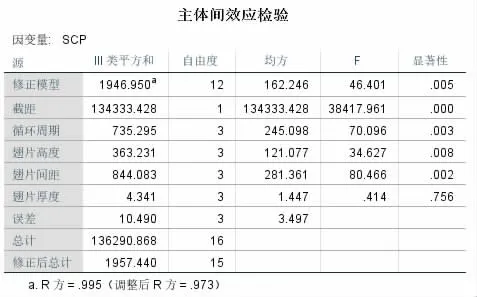
图7 以SCP 为目标函数方差分析结果

图8 以COP 为目标函数方差分析结果

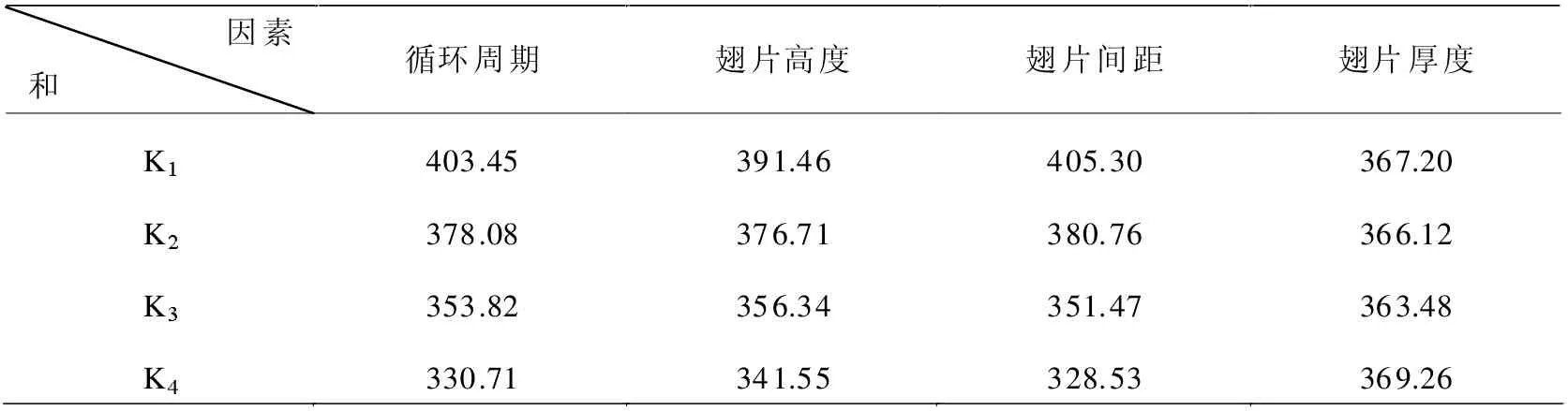
表6 各因素各水平SCP 之和统计表

表7 各因素各水平COP 之和统计表

本文构建了二维翅片管式吸附床瞬态吸附模型，通过设计正交实验评估四个参数（循环周期、翅片高度、翅片间距、翅片厚度）吸附床性能（SCP、COP）的影响，研究考虑了吸附剂内部及外部的传质阻力，忽略了制冷剂气体与吸附剂之间的对流换热，并通过有限元方法计算求解，研究结果如下：

（1）基于SCP 的方差分析结果表明，翅片间距、循环周期对SCP 的影响显著，翅片高度对SCP 的影响接近显著，翅片厚度对SCP 的影响不显著。

（2）基于COP 的方差分析结果表明，在研究参数范围内，仅有循环周期对COP 的影响显著，翅片厚度对COP 的影响接近显著，翅片高度以及翅片间距对COP 的影响程度不显著。

（3）翅片高度、翅片间距、循环周期的增加均会对SCP 带来不利影响，翅片厚度则相反，当循环周期为1000s，翅片高度、翅片间距、翅片厚度分别为10mm、2mm、0.64mm 时，SCP 值最大，为120.09W/kg，COP 为0.43554，这种设计参数可用于低品位热源充足的环境（如：数据中心、热电厂等）。

（4）循环周期的延长会产生更高的COP 值，翅片高度、翅片厚度的增加会导致COP 值降低，翅片间距存在着最优值（2.4mm），当循环周期为1600s，翅片高度、翅片间距、翅片厚度分别为10mm、2.4mm、0.4mm 时，COP 值最大，为0.51185，SCP 为87.24W/kg，这种设计参数可用于低品位热源有限的环境（如：以太阳能驱动的吸附式制冷系统等）。

（5）方差分析结果表明：在研究参数范围内，SCP、COP 均对于循环周期敏感，SCP 对于翅片间距敏感，对于翅片高度较敏感，COP 对于翅片厚度较敏感，综上所述，对于兼顾SCP、COP 的吸附床设计方案，翅片高度及翅片间距的取值应遵从SCP 最优（10mm、2mm）；而翅片厚度的取值应遵从COP 最优（0.4mm），对于循环周期的选取还需再做研究。