基于模糊PID 的热风炉温度控制器设计
2021-01-21刘丕亮习峻豪李爱莲
刘丕亮 习峻豪 李爱莲
(内蒙古科技大学信息工程学院,内蒙古 包头014010)
热风炉在温度快速上升期,合理配置煤气和空气量可以使拱温很快达到设定值。但是热风炉系统不能建立精确数学模型,所以提出模糊控制与PID 结合的方式,这样具备较强的稳定性和快速响应性,提高了系统性能的稳定。
1 数据预处理
为了达到建模的精度要求,有必要对在线采集到的数据进行处理,剔除里面的异常数据,以及计算出一些符合参数的数据,并对它们滤波和归一化处理,对于建模具有重要的意义。
以某钢铁厂3 号4150m3高炉热风炉为例,现场采集了2014 年6 月到2015 年7 月的原始数据,包括顶温、废温、煤气和空气流量、风温,共573823 组数据。原始数据存在大量离群点、缺失与噪声,所以要先对数据进行处理。
1.1 拉依达准则数据滤波
除去噪声的方式有很多,本文研究采用拉依达准则进行数据筛选,用三次样条对缺失数据进行填补。下面对现场采集的数据进行处理:
(1)拱顶温度数据处理
顶温是热风炉重要参数,顶温较低不能保证送风温度,过高会造成拱顶损伤。下面对数据进行仿真,如图1 所示:
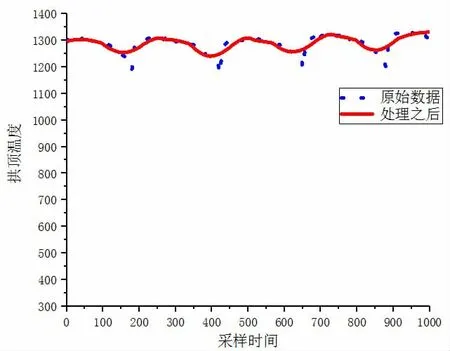
图1 拱顶温度处理前后数据
(2)废气温度数据处理
废温影响着热效率,过高会带走很多热量,过低会使风温较低。下面对数据处理前后的值进行仿真,如图2 所示:
(3)煤气和空气流量数据处理
煤气和空气流量直接影响着热风炉燃烧过程,控制煤气与空气流量空燃比,是决定热风炉燃烧好坏的至关重要的工作。下面对数据处理前后的值进行仿真,如图3 和图4 所示。

图2 废气温度处理前后数据
(4)热风温度数据处理
热风温度与炉顶温度有关,提高炉顶温度可以提高风温。下面对数据处理前后的值进行仿真,如图5 所示:
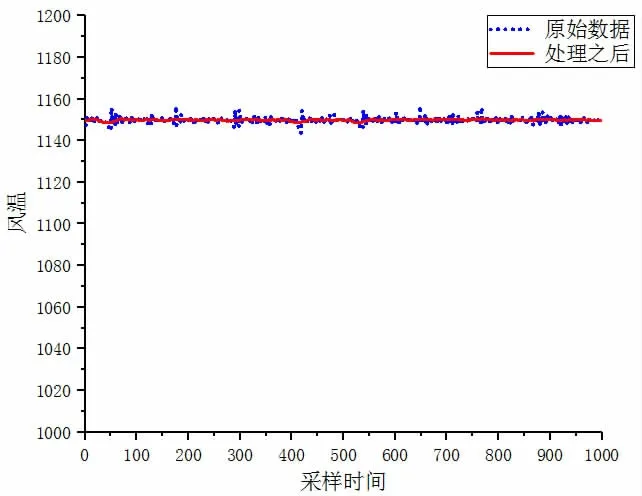
图5 热风温度处理前后数据
1.2 数据分析
由上述对现场数据的处理,可以看出一些问题:
(1)拱顶温度原始数据大约在1190~1320℃,处理后再1300℃,趋于稳定。
(2)废气温度波动较大,原始数据大约在200~430℃,处理后大约在250~350℃波动,满足要求。
(3)煤气与空气流量在时间90 ~110 处存在很大波动,处理后煤气流量大约在7x104附近,空气流量大约在5.6x104附近,趋于稳定。
(4)热风温度波动较小,大约在1150℃左右。
所以从数据分析来看,原始数据总体波动较大,顶温和废温波动大,有优化的空间。因此,可以设计一个模糊PID 控制器对顶温和废温进行控制优化。
2 模糊PID 控制器设计
2.1 模糊PID 控制简介
工业过程控制系统通常用PID 控制器进行控制。
其控制规律如式(1):

传递函数如式2:

式中Kp比例系数;Ti积分时间常数;Td微分时间常数;de/dt为设定值与实际值的差值变化率。
模糊控制是由模糊数学、逻辑的模糊知识和语言推理规则形成的自控系统。它不需要精确数学模型,其结构如图6 所示:

图6 模糊控制硬件结构框图
模糊PID 控制是把PID 和模糊控制基本理论和方法用模糊集表示,用模糊推理实现最佳PID 调整参数。其结构如图7 所示:

图7 模糊PID 控制系统框图
2.2 热风炉燃烧过程分析
燃烧之前,要先预热煤气与助燃空气,一般预热至180~200℃。燃烧过程分为快速燃烧期和蓄热期。在快速燃烧期,通过大量煤气与合适的空燃比快速加热达到顶温设定值,这样可以存储较多的热量。在蓄热期,增加空气流量,调节煤气流量使顶温维持稳定,同时废温不能超过设定值450℃,否则会降低炉体使用寿命,热量损失增大。满足废温和燃烧时间结束就可换炉,准备送风。如图8 所示:
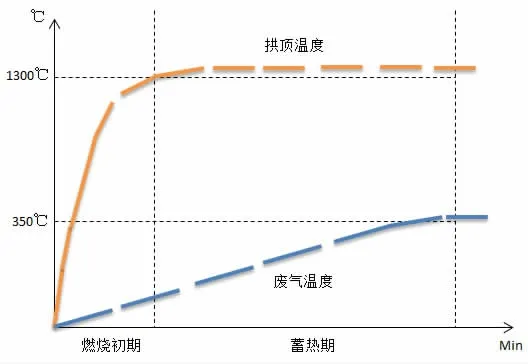
图8 热风炉燃烧过程温度曲线
2.3 模糊PID 控制方法
如图9 所示,外环是温度环,温度PID 参数是由模糊自适应调整,煤气和空气流量环是外环。由图7 可知,r(t)为拱顶温度设定值,温度反馈为温度实际值,e(t)为温度设定值与温度实际值的差值,kp、Ti、Td 分别为温度PID 控制器的比例、积分、微分参数,由模糊自适应控制确定。e(t)和de/dt 作为模糊自适应控制器的输入。
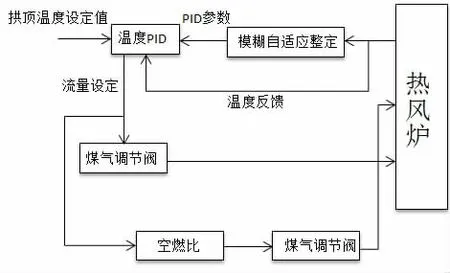
图9 温度控制系统方框图
2.4 模糊PID 控制器设计
自适应模糊PID 控制是我们较常采用的控制方法。它的设计和工作包括以下步骤:
(1)输入、输出变量的确定
以误差e 和误差变化率ec 作为输入,控制量增量U 为输出。其中e=r-y,ec=de/dt。
(2)基本论域、量化论域、模糊子集
①e 的基本论域为:[-60,60]℃
e 的量化论域为:x = { -3,-2,-1,0,1,2,3}
e 的量化因子为:Ke= 3/60=1/20
e 的模糊子集为:{NB,NM,NS,ZO,PS,PM,PB}
②ec 的基本论域为:[-20,20] ℃
ec 的量化论域为:y={-3,-2,-1,0,1,2,3}
ec 的量化因子为:Kec= 3/15=1/5
ec 的模糊子集为:{NB,NM,NS,ZO,PS,PM,PB}
③U 的基本论域为:[0%~100%]
U 的量化论域为:V = {-2,-1,0,1,2,}
U 的量化因子为:KU= 4/100=1/25
U 的模糊子集为:{NB,NM,NS,ZO,PS,PM,PB}
(3)隶属函数
三个变量都使用三角形隶属函数,其相应表示如图10 所示:
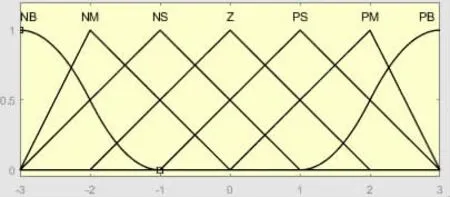
图10 隶属函数分布图
(4)模糊控制规则
根据经验总结出49 条规则,其模糊控制规则如表1 所示:
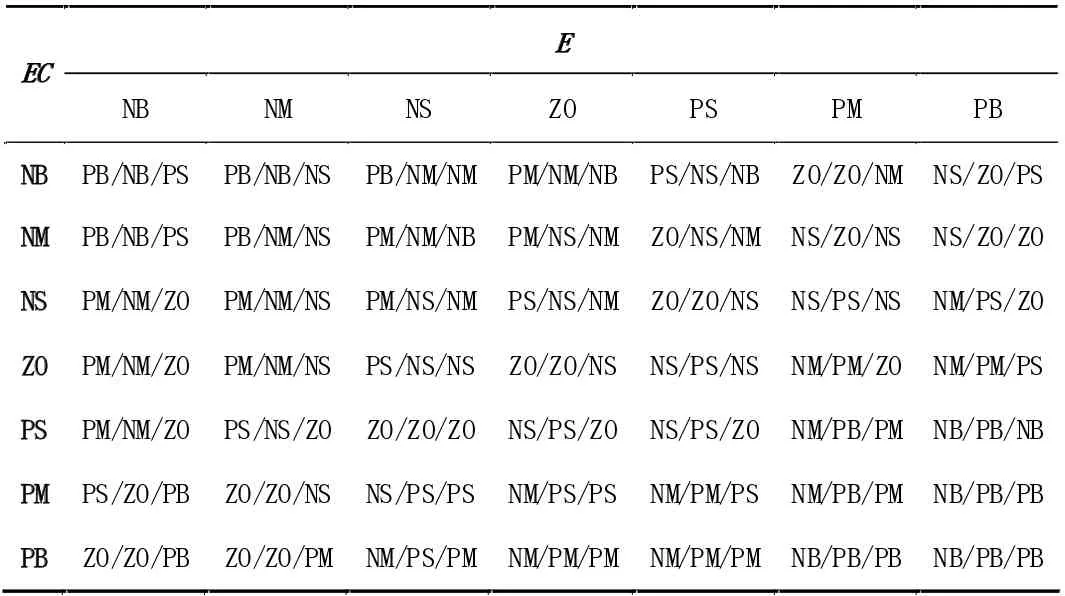
表1 模糊控制规则表
(5)模糊推理
给定的规则集为:
R1:if x=A 1 and y=B 1 then z=C1
R2:if x=A 2 and y=B 2 then z=C2
…
Rn:if x=A n and y=B n then z=Cn
(6)解模糊
解模糊是模糊化的反过程,解模糊的任务就是根据结论确定一个z0;解模糊化平均加权法最简单,如果将变量z 各模糊集合的隶属函数定义为单点时,模糊规则成为:
Ri:ifx=Aiand y=Bithen z=zi
3 模糊PID 控制器仿真研究
在控制仿真前,要建立以热风炉温度为控制对象数学模型,以此模型进行仿真。
3.1 仿真模型的建立
由热风炉燃烧工艺可知,燃烧一段时间后才能检测到顶温变化,所以热风炉温度变化规律一般可用一阶惯性纯滞后环节来表示,为了确定热风炉数学模型,通常可采用飞升曲线法来获得被控对象的模型,其传递函数可表示为:
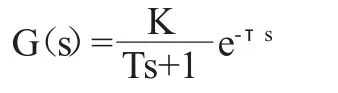
其中,K 静态增益,T 时间常数,τ 滞后。
利用飞升曲线法获得对象飞升曲线,然后用Cohn-Coon 公式求它的参数,其飞升曲线如图11 所示:
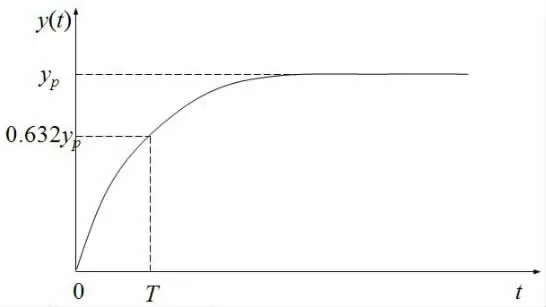
图11 飞升曲线
飞升曲线法:输入量(ΔM=M2-M1)由系统记录输出变化率量(ΔC=C2-C1)Cohn-Coon 公式如下:
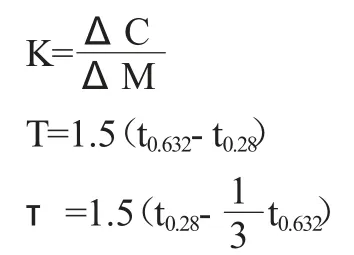
式中,K 放大系数,T 时间常数,τ 滞后,ΔM 阶越输入,ΔC 输出响应,t0.28飞升曲线0.28ΔC,t0.632飞升曲线0.632ΔC。
热风炉工艺条件要求如下:热风炉数量:4 座;风量:7400Nm3/min;风温(最高):1300℃;送风压力:0.525MPa;顶温(最高):1350℃;废温(最高):450℃。煤气量取最大流量范围0~621600m3/h,最大流量则约为172.7m3/s。顶温最高不能超过1350℃,采用最大流量往热风炉输送煤气,则K=1450/172.7≈7.8。设定稳态值为1300℃,稳态增益K=7.8,惯性时间常数T=300s,传递函数可以表示为:
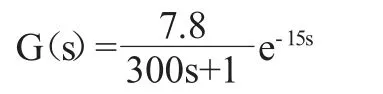
其simulink 模糊PID 控制器仿真模型如图12 所示:

图12 模糊PID 控制器simulink 仿真模型
3.2 仿真结果
运行Matlab 中simulink 仿真模型,模糊PID 控制仿真曲线如图13 所示:
由图13 可知,黄色曲线是PID 控制,红色曲线是模糊PID 控制。图13 可知,PID控制超调量约26%,上升时间约50s,调节时间约140s;而模糊PID 控制超调量约19%。上升时间约35s,调节时间约80s。所以仿真结果表明,用模糊PID 控制比PID 控制在响应速度和调节时间都更加快速,稳定性更好。所以用模糊PID 对温度控制速度快,精度高,稳态性能好,控制效果很好。
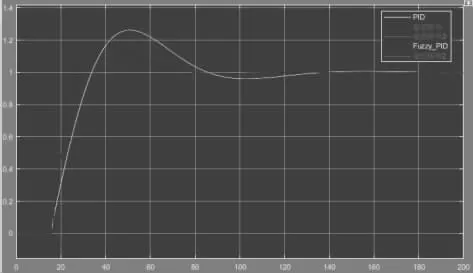
图13 PID 控制和模糊PID 仿真曲线
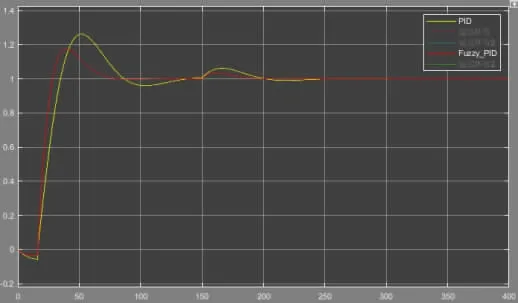
图14 加入扰动的仿真对比
现在时间150s 处加一个扰动,比较两者的调节情况,如图14 所示。
由图14 中可以看到,模糊PID 控制调节扰动更好,更加稳定性。
4 结论
通过对拱顶温度模糊PID 控制器设计,保证了热风炉在正常工况条件下和存在干扰波动情况下,都能稳定地使煤气和助燃空气保持在一定偏差范围内,实现燃烧过程对温度稳定性的控制。
