人字槽狭缝节流动静压混合气体轴承的设计研究
2021-01-21于贺春张国庆王文博王仁宗王东强
于贺春,张国庆,王文博,王仁宗,王东强
(中原工学院 机电学院,郑州 450007)
气体轴承因具有高精度,低摩擦和高转速等优点,广泛应用于高精度和高转速设备中,如高速机床和涡轮机械[1-4]。其中,动静压混合气体轴承结合了静态轴承和动态轴承的优点,可以在较宽的温度范围内工作并具有较大的载荷和高速能力,同时可避免转子与轴承在起动和停止过程中的摩擦,使其在高速工作条件下具有较好的动态特性[5-9]。
Dee C W等[10]首先提出了狭缝节流气体轴承,并利用有限元法对其进行了研究。Yoshimoto S等[11-12]提出了一种圆周狭缝气体轴承,利用数值分析和实验两种方法研究了该轴承的静态特性。Sharma SC等[13]研究了一种适用于不可压缩流体的径向滑动轴承,并得出与带有毛细管节流孔和定流量节流器的非对称孔入口的径向滑动轴承相比,非对称槽布置可以提供较好的速度稳定性阈值裕度的结论。Tomohiko I等[14]提出并研究了一种轴向设置限位槽的气体静压轴颈轴承,并提高了该轴承的刚度。Pankaj K等[15]在考虑热效应和微极润滑油共同影响的情况下,对孔入口和槽入口混合轴颈轴承的性能进行了比较研究,结果表明:在给定的润滑油微极参数范围内,在最大流体压力和动力系数方面,恒流量阀补偿孔入口混合轴颈轴承的性能最高。Chandra B K等[16]分别对用不同节流器补偿的双叶形/圆形非凹入式混合轴颈轴承进行了ER流体润滑和表面变形对其性能的综合影响的对比研究。研究表明:ER流体润滑的CFV补偿双叶形(δ=1.1)非凹入式径向滑动轴承相对于其他补偿元件(如毛细管,节流孔和槽口)具有卓越的性能。Wan Jun Mei等[17]提出了一种描述流体润滑非对称人字槽径向轴承中槌形流体流动现象的数值模型,并采用“随槽”网格变换方法来捕获所有的槽边界。Chen S K等[18]研究了带人字槽套筒的液体动压径向微轴承的稳定性,得到了各种设计参数的最优值,以最大限度地提高承载能力和稳定性。Miyanaga N等[19]采用线性摄动分析和非线性瞬态分析方法,研究了黏弹性支承刚度和阻尼对人字槽气体轴承稳定性特性的影响。研究表明,在黏弹性支承下,槽形结构的变化可以提高涡动失稳的临界转速。为了解决空穴区域的自由边界问题,Chen C Y等[19]在雷诺方程中引入了一个附加项来稳定求解。结果表明:增加附加项可以得到准确的压力分布,有利于槽形和尺寸的选择。Xiang Guo等[20]提出了一种研究微槽径向轴承润滑性能的瞬态流体动力润滑模型。结果表明:人字槽轴承在正轴向运动时表现出最大的承载能力,其次是直槽轴承,最后是螺旋槽轴承。
基于上述研究,本文提出了一种人字槽狭缝节流动静压气体轴承。采用以有限差分法为基础的Matlab程序研究了轴承结构参数和工作参数对动态特性的影响,并根据正交实验设计法和灰色理论对轴承参数进行了优化,得到轴承结构参数和工作参数对轴承动态特性影响的顺序以及轴承特性最佳时的轴承参数组合。
1 轴承结构和工作原理
动静压轴承-转子系统的结构如图1所示。压缩气体通过狭缝节流器进入气膜间隙,支承转子运动。在轴承转子系统的启动和停止过程中,动静压轴承的静压效应支撑转子运动,在稳定工作过程中,转子受人字槽动压效应的支持,可降低供给压力,从而保证转子在整个运动过程中的稳定。
2 数学模型
人字槽狭缝节流动静压气体轴承的理论计算分析包括2个部分:狭缝节流器的流场计算和气膜间隙的流场计算。
2.1 狭缝节流器的流场计算
当气体流经狭缝节流器时,热交换非常小,并且节流器的宽度是微米级。根据节流器的这两种特性,可以将气体在狭缝节流器的流动简化为气体在2个平板中的一维流动[11-12]。假设气体沿x方向以速度u流动,2个平板之间的垂直距离可以认为是人字槽宽度Z,平行板的长度与人字槽深度H相同,平板的宽度等于狭缝的弧长。气体在平板间的流动的模型如图2所示。
当气体流场为一维稳定流场时,Naiver-Stokes方程和状态方程可以分别简化为式(1)和式(2)。
根据相应的边界条件和积分方程方法,式(1)可以转化为
平板间气体的质量流量为
由式(2)和式(3)可以得到
人字槽的总气体质量流量可利用式(6)计算。
2.2 气膜间隙的流场计算
由于气膜厚度比轴承半径小3~4个数量级,因此可以忽略圆柱面曲率的影响,将圆柱轴承的气膜展开成平面。根据狭缝的数量,将气膜间隙平均分成N等份,每等份的宽度为b2。为了简化计算,引入假设条件:①气膜厚度在每等份是恒定的;②两狭缝之间没有气体流动,气体从节流器流出后,立即填充每等份;③不考虑圆周方向的气体流动;④气膜间隙中每等份压力相等并等于气体从节流器流出时的压力。图3为气膜间隙的展开图,并通过式(7)计算每等份的质量流量M。
根据相应的边界条件和积分方法,得到
根据式(2)和式(8)得到
通过式(10)获得气膜间隙的气体总质量流量。
忽略气体狭缝之间和气膜间隙的扩散流和周向流动,狭缝节流器的气体质量流量与气体间隙中的气体质量流量满足
节流器出气口的压力可以根据式(12)计算。
2.3 有限差分法求解雷诺方程
气膜间隙中的压力分布可以利用雷诺方程(13)计算。
量纲为一化雷诺方程可以离散为
根据人字槽的特殊形状,采用平行四边形网格并人字槽方向网格划分。平行四边形网格如图4所示,其中Δx和Δy满足
具有人字槽的区域的气膜厚度可以通过式(16)计算。
其他区域的气膜厚度可以通过式(17)计算。
通过有限差分法和五点差分法对雷诺方程进行离散,图5所示为五点差分法原理图,式(18)为雷诺方程的差分表达式。
其中,系数A1、A2、A3和A4均与气膜厚度和气膜压力有关。
2.4 基于旋转坐标系的动态特性计算
当转子高速旋转时,转子有旋转和涡动现象。转子涡动导致压力场和速度场沿圆周方向变化,从而产生气膜力F,气膜力F受转子位移和速度的影响。因此,采用旋转坐标系计算轴承的动态特性,图6所示为旋转坐标系。
假设转子的偏心量为e,其涡动轨迹为圆,假设坐标系以与转子同样的涡动角速度Ω,并且转子涡动角速度为0,计算域几何形状将不会变化,故网格也不会发生变化。由此消除了控制方程中的时间相关项,将非定常问题转化为定常问题来求解,那么此时转子的速度扰动大小为eΩ。
气膜力Fr0和Ft0由式(19)计算
气膜力Fr0和Ft0,偏心量e和速度扰动之间的关系是非线性的。在计算气膜力Fr1和Ft1时,扰动分为两部分。其中,一部分是没有速度扰动的气膜力Fr1和Ft1;另一部分则为该状态附近的小扰动Δe和ΔΩ带来的气膜力Fr1和Ft1。如果将此时的气膜力Fr1和Ft1在该状态附近用泰勒级数展开,如式(20)所示
根据气膜力F的结果,可以求解阻尼系数和刚度系数,具体步骤如下:
1)阻尼系数的计算
当转子速度n一定,转子的偏心度为e1,旋转角速度为Ω,可以获得气膜力Fr0和Ft0。给定微小的速度扰动ΔΩ,此时偏心率e1不变,根据Fr0和Ft0以及Fr1和Ft1计算出新的气膜力Fr1和Ft1,轴承的阻尼系数可以通过式(21)求解。
2)刚度系数的解
给定微小的偏心扰动Δe,转子速度和旋转角速度保持不变,根据气膜力Fr0和Ft0以及Fr2和Ft2可以计算出新的气体膜力Fr2和Ft2。轴承的刚度系数可以通过式(22)求解。
2.5 计算过程和计算参数
利用Matlab软件编程进行计算。计算流程如图7所示,轴承的计算参数见表1。

表1 人字槽狭缝节流动静压气体轴承的计算参数
3 计算结果
3.1 人字槽狭缝节流动静压气体轴承和普通轴承的动态特性比较
为了对比研究人字槽狭缝节流动静压气体轴承和普通轴承的动态特性,按照表1中的参数,在0.1~0.7范围内改变轴承偏心率,其他参数保持不变,计算分析后的动态特性曲线如图8所示。其中,图8(a)显示了不同偏心率ε下人字槽狭缝节流动静压气体轴承和普通轴承的主阻尼,从曲线可以看出:2种轴承主阻尼均随偏心率ε的增大而增加,但人字槽狭缝节流动静压气体轴承的主阻尼大于普通轴承的主阻尼。图8(b)显示了不同偏心率ε下人字槽狭缝节流动静压气体轴承和普通轴承的交叉阻尼,两种轴承的交叉阻尼随偏心比的增大而减小,人字槽狭缝节流动静压气体轴承的交叉阻尼小于于普通轴承的交叉阻尼。图8(c)显示了不同偏心率ε下人字槽狭缝节流动静压气体轴承和普通轴承的主刚度,当偏心率ε<0.4时,两种轴承的差值较小;当偏心率ε>0.4时,差值随偏心率ε增加而增大。图8(d)显示了不同偏心率ε下人字槽狭缝节流动静压气体轴承和普通轴承的交叉刚度,交叉刚度随偏心率ε增加而增加,并且人字槽狭缝节流动静压气体轴承的交叉刚度增加明显高于普通轴承。
3.2 转子转速对动态特性的影响
为了研究不同转速对轴承动态特性的影响,按照表1中的参数,在6 000~120 000 r/min范围内改变转子速度,在0.1~0.7范围内改变轴承偏心率,其他参数保持不变,计算分析后的动态特性曲线如图9所示。其中:图9(a)显示了主阻尼的变化曲线,随着转子速度n的增大,在相同的偏心率ε下,主阻尼增大,但随着速度的增大,偏心率ε对主阻尼的影响变小。图9(b)显示了交叉阻尼的变化曲线,随着速度的增加,在相同的偏心率ε下,交叉阻尼减小,随着速度的增加,偏心率ε对主阻尼的影响减小。图9(c)显示了主刚度的变化曲线,当偏心率ε≤0.5时,随着速度的增加,主刚度增加,但增加量减小,然而,当偏心比率ε>0.5时,主刚度的变化趋势相反,减小量变大。图9(d)显示了交叉刚度的变化曲线,转子速度越小,交叉刚度在相同的偏心率ε越大,随着转子速度的增加,偏心率ε对轴承交叉刚度的影响变小。
3.3 轴承长径比对动态特性的影响
为了研究不同轴承长径比对轴承动态特性的影响,按照表1中的参数,在0.8~1.6范围内改变轴承长径比,在0.1~0.7范围内改变轴承偏心率,其他参数保持不变,计算分析后的动态特性曲线如图10所示。其中:图10(a)显示了长直径比L/D对主阻尼的影响,随着长直径比L/D的增加,在相同偏心比下主阻尼增加。图10(b)显示轴承长径比L/D对交叉阻尼的影响:当L/D=1时,轴承的交叉阻尼值基本不变;当L/D<1时,交叉阻尼随着偏心度的增加而增加;当L/D>1时,交叉阻尼的变化趋势相反。图10(c)和(d)显示了轴承长径比L/D对主刚度和交叉刚度的影响,随着轴承长径比L/D的增加,在相同的偏心比下,主刚度和交叉刚度均增加。
3.4 人字槽宽长比对动态特性的影响
为了研究不同人字槽宽长比对轴承动态特性的影响,按照表1中的参数,在0.15~0.3范围内改变人字槽宽长比,在0.1~0.7范围内改变轴承偏心率,其他参数保持不变,计算分析后的动态特性曲线如图11所示。其中,图11(a)显示了人字槽的宽长比b/l对主阻尼的影响,在相同的偏心率下,主阻尼随着人字槽的宽长比b/l的增大而增大。图11(b)人字槽的宽长比b/l对交叉阻尼的影响,相同的偏心率下,主阻尼随着人字槽的宽长比b/l的增大而减小,然而,当偏心率 ε>0.4,人字槽的宽长比b/l=0.3时的交叉阻尼要大于人字槽的宽长比b/l=0.25时的交叉阻尼。图11(c)显示了人字槽的宽长比b/l比对主刚度的影响,相同的偏心率下,主刚度随着人字槽的宽长比b/l的增大而减小,当偏心率ε>0.5时,人字槽的宽长比b/l=0.3时的主刚度要大于人字槽的宽长比b/l=0.25时的主刚度。图11(d)显示了人字槽的宽长比b/l对交叉刚度的影响,当偏心率ε<0.5时,相同偏心率下,交叉刚度随着人字槽的宽长比b/l的增大而增大;当偏心率ε>0.5时,交叉刚度的变化趋势是相反的。
3.5 人字槽深度对动态特性的影响
为了研究不同人字槽深度对轴承动态特性的影响,按照表1中的参数,在0.55~1范围内改变量纲为一化人字槽深度,在0.1~0.7范围内改变轴承偏心率,转子速度为120 000 r/min,轴承长径比为0.8,人字槽的宽长比为0.3,其他参数保持不变,计算分析后的动态特性曲线如图12所示。其中:图12(a)显示了人字槽深度对主阻尼的影响,当偏心率ε>0.2时,主阻尼几乎随人字槽深度的增加而线性增加。图12(b)和(c)分别显示了人字深度对交叉阻尼和主刚度的影响,当偏心率ε≤0.4时,交叉阻尼和主刚度均随人字槽深度的增加而增加;当偏心率ε>0.4时,交叉阻尼和主刚度的变化趋势相反。图12(d)显示了人字槽深度对交叉刚度的影响,在相同的偏心率下,交叉刚度随着人字槽深度的增加而增加。
3.6 狭缝宽度对动态特性的影响
为了研究不同狭缝宽度对轴承动态特性的影响,按照表1中的参数,在0.012~0.024范围内改变量纲为一化狭缝宽度,在0.1~0.7范围内改变轴承偏心率,转子速度为120 000 r/min,轴承长径比为0.8,人字槽的宽长比为0.3,量纲为一化人字槽深度为1,其他参数保持不变,计算分析后的动态特性曲线如图13所示。其中:图13(a)显示了狭缝宽度对主阻尼的影响,在相同的偏心率下,主阻尼随着狭缝宽度的增大,几乎呈线性增长;图13(b)显示了狭缝宽度对交叉阻尼的影响,在相同的偏心比下,交叉阻尼随着狭缝宽度的增加而减小;图13(c)显示了狭缝宽度对主刚度的影响,在相同偏心率下,主刚度随着狭缝宽度的增加而增加;图13(d)显示狭缝宽度对交叉刚度的影响,在相同的偏心率下,交叉刚度随着狭缝宽度的增加而增加。
4 轴承结构优化
根据上述计算结果,采用5因素4水平的正交实验法和灰色理论对轴承进行优化设计。通过优化得到了使轴承主阻尼和主刚度最大时的轴承参数组合以及轴承参数对轴承动态特性的影响顺序。
4.1 正交实验设计
设定转子速度n,轴承长径比L/D,量纲为一化人字槽深度 ¯hg,人字槽宽长比b/l,量纲为一化狭缝宽度¯Z为正交实验的5个因素,这些参数的4个不同取值表示因素的不同4水平。正交实验设计表L16(45)和仿真结果分别如表2、3所示。
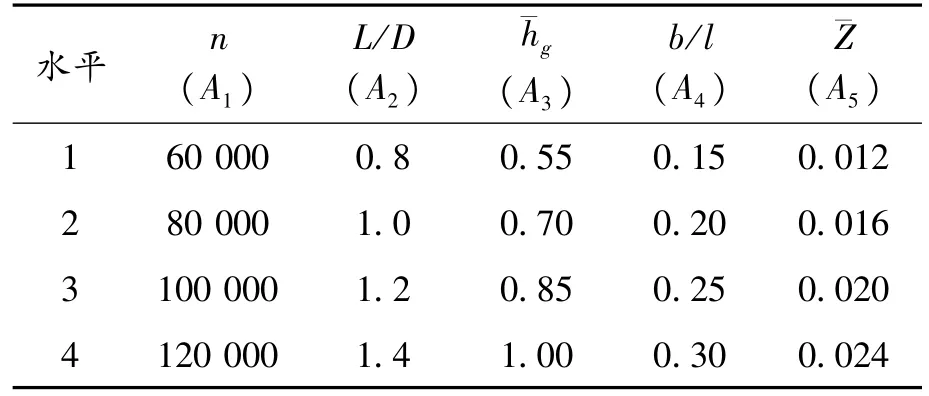
表2 正交实验设计表L16(45)
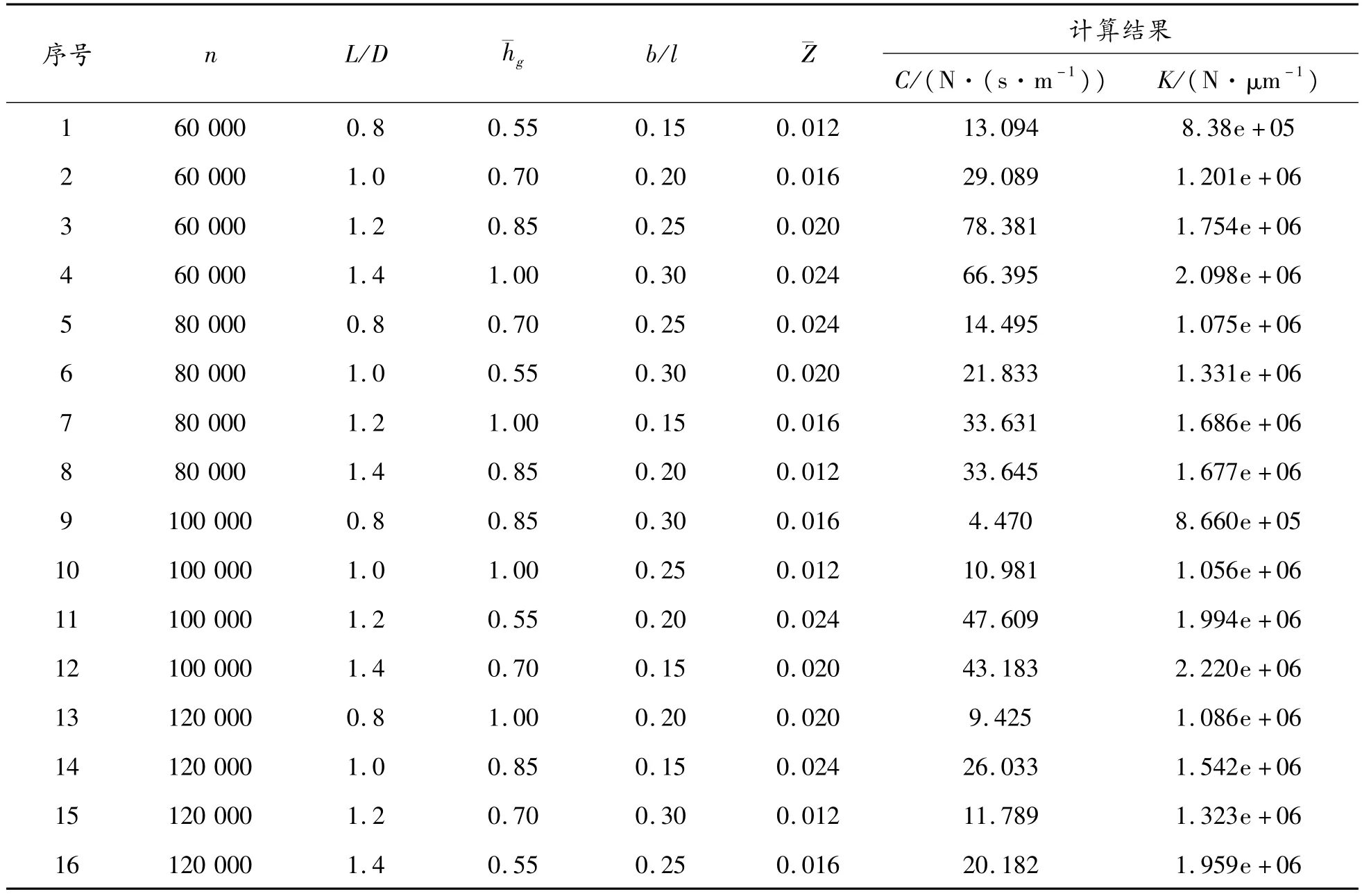
表3 仿真结果
4.2 灰色理论分析
利用灰色理论对正交实验表中的数据进行了分析和计算。从分析结果可以得到轴承参数对轴承动态特性的影响顺序和轴承特性最佳时的轴承参数组合。
根据主阻尼越大,主刚度越大,轴承动态特性越好的原理。表3中的数据由式(23)进行预处理,预处理结果如表4所示。
其中,φ=0,1,…,n;n为试验的次数;ξ=1,2,…,m;m为数据序列参数的个数。
利用式(24)计算比较序列相对于参考序列在第φ点绝对差,计算结果如表5所示
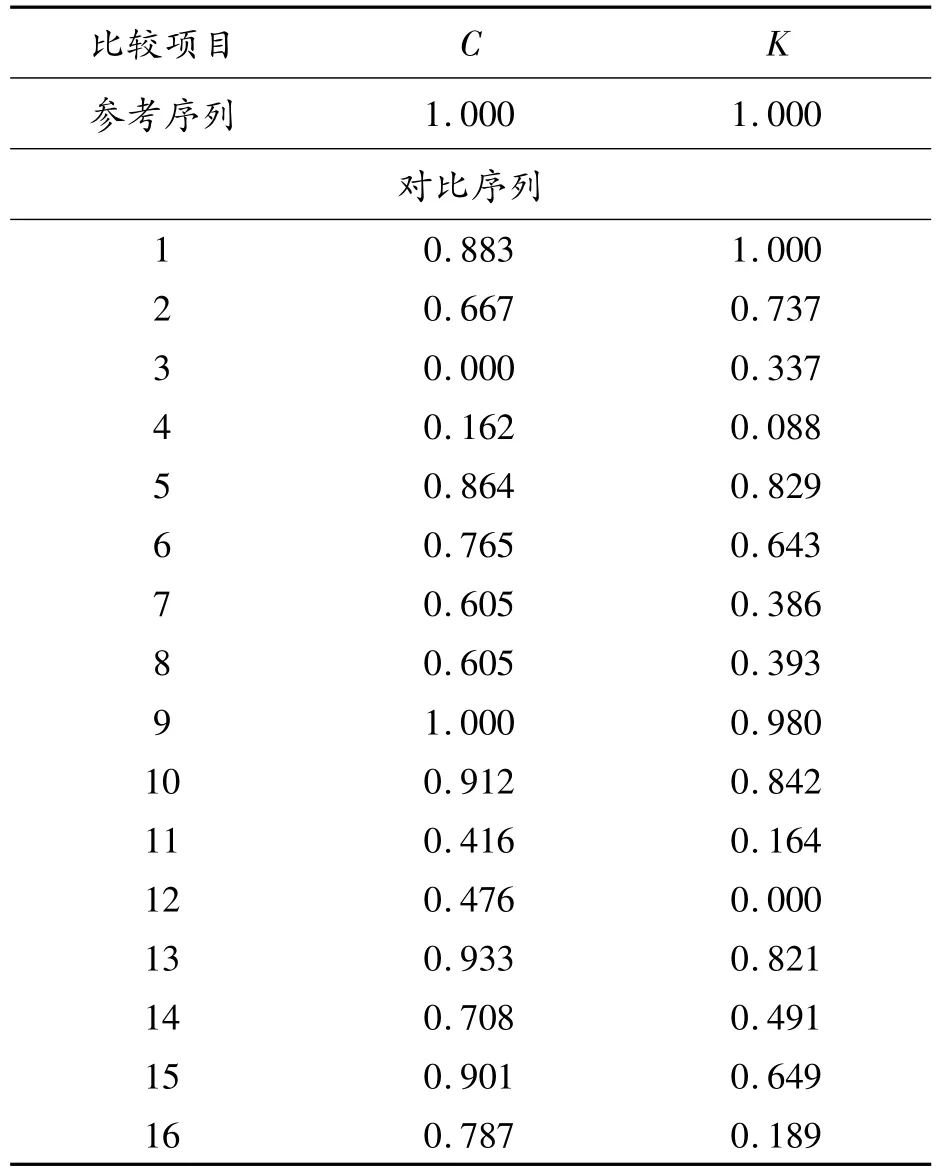
表4 预处理结果
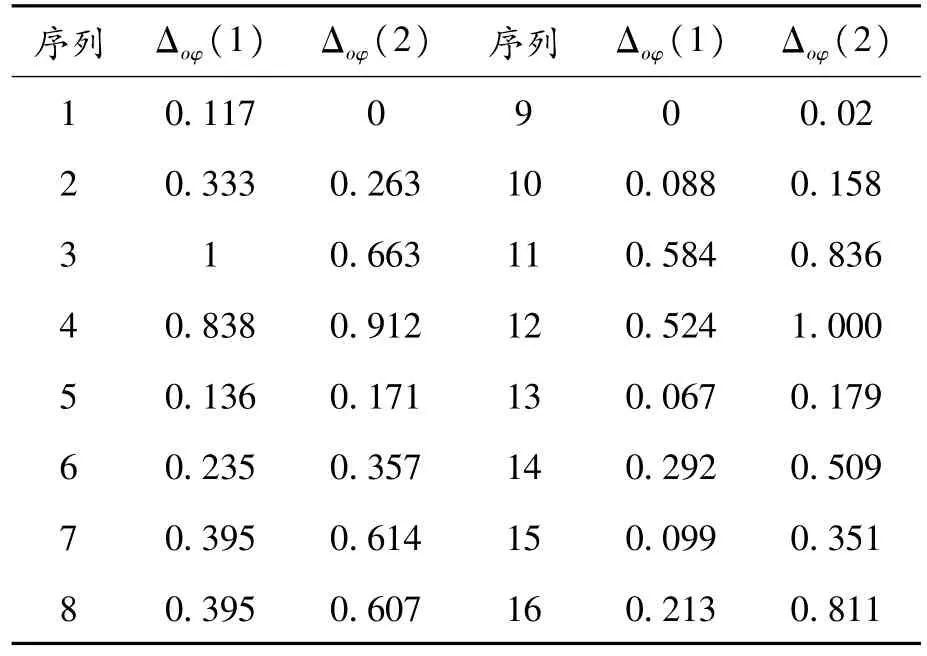
表5 绝对差计算结果
在正交试验中,假设评价各因素参数水平相同,则权重因子ζ=0.5,将该因子代入灰色关联系数和灰色关联度计算式(25)和式(26),计算结果如表6所示。

表6 灰色关联系数和灰色关联度值
如表6所示,序列号16的灰色关系系数最小,换言之,当转子速度n=10 000 r/min,轴承直径比L/D=0.8,量纲为一化人字槽深度=0.85,人字槽宽长比b/l=0.3,量纲为一化狭缝宽度=0.016时主阻尼和主刚度最大。
根据灰色关系系数和灰色关联度值的计算结果,计算了不同水平各参数的平均灰色关联度,计算结果如表7所示。最大值与最小值的差值越大代表该参数对轴承静承载力和静刚度的影响越显著,通过不同参数的灰色关联度差值比较得到轴承的不同因素对轴承动态特性的影响的大小顺序为:轴承长径比L/D,狭缝宽度Z,轴承转速n,人字槽宽长比b/l和人字槽深度hg。
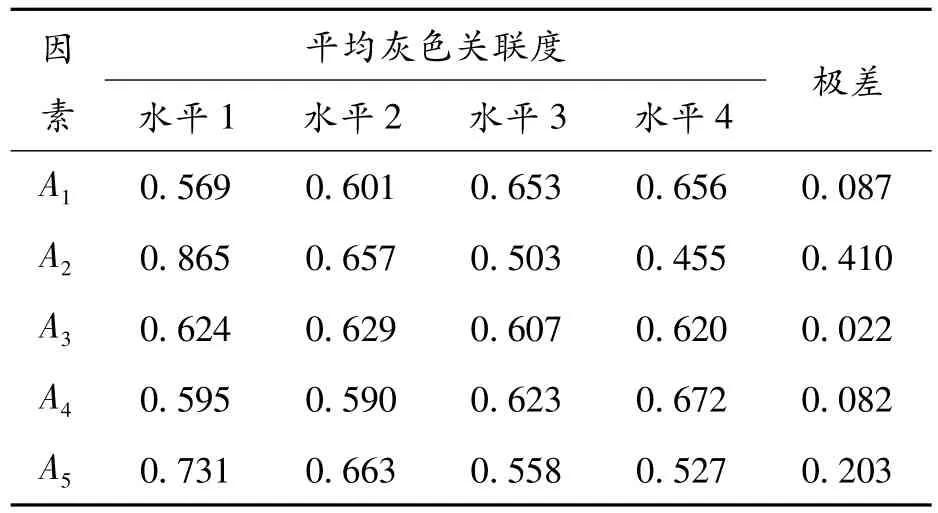
表7 各参数因素各水平的平均灰色关联度
5 结论
1)在相同偏心率ε下,人字槽狭缝节流动静压气体轴承的阻尼要大于普通轴承。轴承长径比L/D,狭缝宽度Z,轴承转速n,人字槽宽长比b/l,和人字槽深度hg等轴承参数取适当值时,可以得到轴承的最佳动态特性。
2)当转子速度n=10 000 r/min,轴承直径比L/D=0.8,量纲为一化人字槽深度=0.85,人字槽宽长比b/l=0.3,量纲为一化狭缝宽度=0.016时,轴承的主阻尼和主刚度最大。轴承参数对轴承动态特性的影响顺序是轴承长径比L/D,狭缝宽度Z,轴承转速n,人字槽宽长比b/l和人字槽深度hg。
