基于稀疏采样的无线多媒体传感网图像压缩算法

郭 剑，韩 崇，施金宏，薛浩天，孙力娟

(南京邮电大学 a.计算机学院，b.江苏省无线传感网高技术研究重点实验室，南京 210003)

无线多媒体传感器网络(WMSNs)是一种由大量低成本传感器节点通过无线通信组成的自组织网络系统。这些节点通常配备有麦克风、摄像头以及其他传感器来收集多媒体数据[1]。随着互补金属氧化物半导体(CMOS)和低成本无线网络技术的日益成熟，WMSNs现已被广泛应用于图像采集、视频监控等领域[2]。由于WMSNs可以捕获到更多维的数据，获得的数据量更大，因此，处理和传输时所需的节点能耗也会随之激增。然而，对于布置在恶劣自然环境中的WMSNs，其节点能量有限且难以进行补充。一旦电池耗尽，节点将无法正常工作，有限的能源存量已经成为限制WMSNs发展的瓶颈之一。因此，设计适合的压缩方案来降低传输的能耗是非常必要的[3]。

为了延长节点的生存时间，相关研究者已经提出许多压缩算法来抑制传输的数据量。PHAMILA et al[4]设计了一种基于小波域的低比特率图像压缩方案；PAL et al[5]通过引入基于颜色滤波器阵列(CFA)的图像压缩方案来解决WMSNs的能源短缺问题；MAMMERI et al[6]提出了一系列低能耗的JPEG图像传输方案。这些方案旨在通过分析图像并丢弃其中的非必要元素来减少数据量，从而使能量消耗最小化。因此，分布式图像压缩算法作为一种低能耗的WMSNs压缩方案，受到了广泛的关注。WU et al[7]基于小波变换设计出一种用于资源受限的多跳无线网络的低能耗分布式图像压缩方案；鲁琴等[8]提出采用双正交重叠变换[9]和JPEG2000方法的低能耗多点协作图像压缩方法；韩崇等[10]提出了基于奇异值分解(singular value decomposition，SVD)的压缩和传输图像的分布式图像压缩。上述相关研究成果已经在数据压缩方面取得了很好的成效，然而，这些方案在数据采集的编码端依然包含有较复杂的计算工作，这样就会导致有限供电的传感器节点在图像处理过程仍旧需要大量的能源消耗。因此，图像数据处理部分能耗仍需要进一步优化。压缩感知技术的兴起，提供了另一种有效的图像采集和压缩方式[11]。ZHANG et al[12]提出了一种面向无线图像传感器网络的随机采样分块压缩感知图像压缩算法。ZHANG et al[13]针对图像恢复问题进行研究，提出了基于低秩近似的多媒体传感网压缩感知方法。但这些算法并未考虑压缩感知算法中采样矩阵的优化选择问题，容易造成图像恢复效果不足的问题。

基于上述分析，本文结合WMSNs的特点，考虑多传感器节点的协作性，通过引入压缩感知技术，实现图像在傅里叶域上的分块自适应压缩采样与传输，通过对图像采集时采样矩阵的优化设计，提出了一种基于傅里叶域稀疏采样的分布式多媒体传感网图像压缩算法。

1 预备工作

1.1 压缩感知框架

传统图像信号编解码方式以奈奎斯特采样定理为基础，其采样过程与压缩过程是相对独立的。在编码端一般先对信号进行独立采样，然后对采集到的信号数据进行变换(如DCT变换、小波变换等)，变换后得到重要系数的幅度和位置信息，通过运算找出其中的大量小值数据并丢弃，从而实现图像信息的压缩。但该解码方式在图像的压缩编码阶段通常会涉及大量的矩阵运算和数据统计，对系统的计算能力和存储资源有一定的要求，不能直接应用到能量供应受限的WMSNs中。

压缩感知不同于传统编解码方式，其最大的特点是以压缩采样的方式代替传统压缩算法中涉及的复杂变换计算，这种采样和压缩同时进行的过程被称为压缩编码。理论上，只要原始信号是稀疏的，压缩感知方法就可以用远低于奈奎斯特标准的速率进行图像采样与处理[14]，同时保证恢复出的图像具有较好的视觉质量。

假设存在稀疏的原始图像信号表示为s，其列向量长度为N.可以使用观测矩阵Φ以压缩采样的方式对稀疏信号s直接进行观测采样，得到的观测值为y，其列向量长度为M，且M远小于N.它们之间的关系具体可以表述为：

y=Φs.

(1)

但是，实际情况下原始信号无法保证绝对是稀疏的，对于原始信号非稀疏的情况，可以通过稀疏变换的方式以稀疏系数来表示。假设存在非稀疏的自然图像信号x，其稀疏系数可以表示为：

s=Ψx.

(2)

式中：Ψ表示信号的稀疏变换过程，被称为稀疏矩阵。由于式(2)是一个欠定方程，无法直接对x进行求解。此时可以将式(2)转为一个约束条件，使s在最稀疏时可以获得x的最优解，具体可以表示为：

(3)

将上式中的观测矩阵Φ和稀疏矩阵Ψ进行组合，可以得到θ=ΦΨ，压缩采样过程可以重新表示为：

y=θx.

(4)

为了保证重建算法的收敛性，使得稀疏系数s可以被测量值有效恢复，式(4)中的矩阵θ应当满足限制等距特征(restricted isometry property，RIP)，即对于任意稀疏矢量v，矩阵θ都能使如下不等式成立：

(5)

由此可见，压缩感知系统的构造需要三个重要条件：1) 稀疏表示，即利用稀疏矩阵或稀疏变换使原始图像数据在变换域中仅有较少的非零系数，在本文中涉及的稀疏表示方法主要为傅里叶变换；2) 线性测量，即利用满足RIP条件的测量矩阵从原始图像数据中提取出测量值；3) 非线性重构，利用少量稀疏测量值计算信号的稀疏表示系数。

1.2 傅里叶变换

在图像处理领域，图像的频率是一种十分重要的要素，作为灰度在平面空间中梯度的表现，它能够反映出图像中灰度变化的剧烈程度。对于图像而言，其在空间域中的表现方式为灰度分布函数。而在频域中时，图像则通过频率分布函数来表示。在满足一定条件的情况下，可以利用傅里叶变换与傅里叶反变换来实现在图像在空间域与频率间的互换。也就是说，傅里叶变换及其逆变换可以实现图像灰度分布函数和频率分布函数之间的相互转换。

假设存在一张图像，其在空间域上的灰度分布函数为f(x,y)，那么可以利用二维连续傅里叶变换将图片变换至频域表示：

(6)

式中：F(u,v)是图像的频率分布函数，u、v表示频率变量，分别对应着x轴与y轴；d为积分。

同时，利用二维连续傅里叶反变换也可以进行图像频率分布函数到灰度分布函数的变换：

(7)

在实际应用中，由于图像由大量灰度像素点组合表示，并非绝对连续，这种情况下可以使用二维离散傅里叶变换：

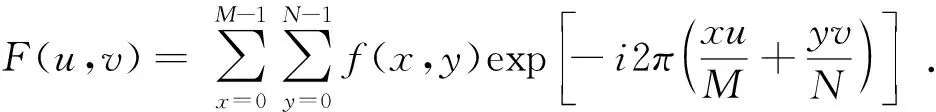
二维离散傅里叶的反变换过程可以表示为：

(9)

图1是利用傅里叶变换对测试图像进行傅里叶域上稀疏表示的效果图。通过对图像在傅里叶域上数据分布的特征进行分析可以发现，傅里叶域图像的中心部分聚集有大量的低频数据，这些数据构成了一块较为集中的低频区域，仅有少部分高频数据分布在图像中心周围。整体来看，傅里叶域上数据稀疏且围绕中心分布。图像在傅里叶域上的这一数据分布特征，使得基于傅里叶域的图像压缩采样成为可能。

图1 图像在傅里叶域上的稀疏表示Fig.1 Sparse representation of image in Fourier domain

1.3 稀疏采样

压缩感知通过稀疏变化的方式将原始图像映射到稀疏域中，使其在稀疏域中拥有尽可能少的非零元素，从而达到使图像信息稀疏化的目的。其中，傅里叶变换便是有效实现图像信息稀疏表达的手段之一。由图像在傅里叶变换域中的数据分布特征可知，其数据分布具有稀疏性，且大量低频信息集中在图像中心位置，这就为图像的压缩收集提供了方便。通过设计适合的观测矩阵对目标图像在傅里叶变换域进行掩膜采样，便可以实现图像的压缩。

完整的傅里叶域图像稀疏采样及重建流程如图2所示。对于非稀疏的原始图像信号x，可以利用稀疏变换(本文使用快速傅里叶变换)将其转换为稀

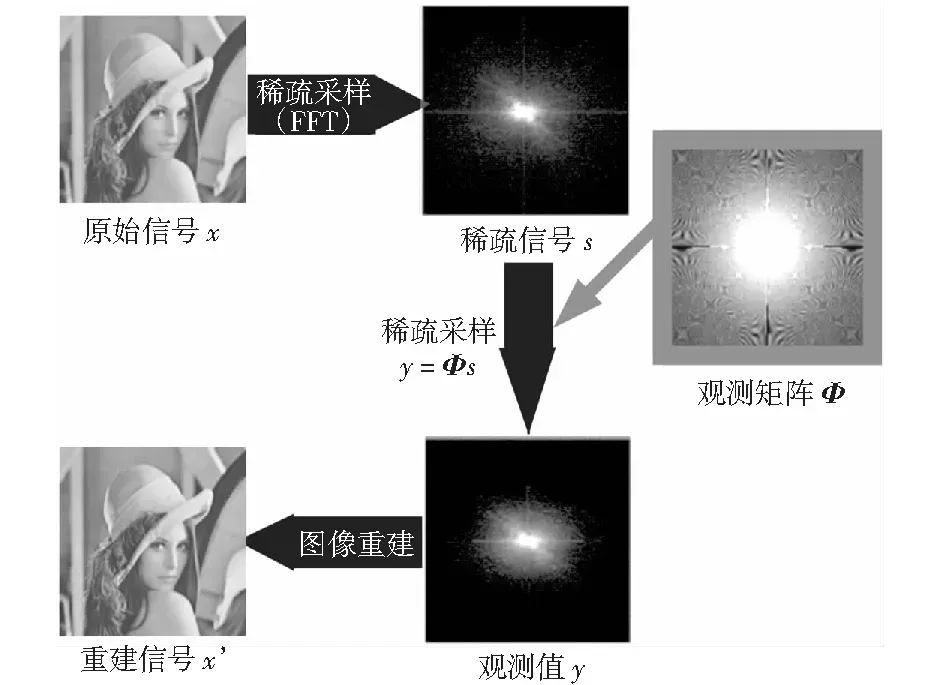
图2 傅里叶域图像稀疏采样及重建流程Fig.2 Sparse sampling and reconstruction of image in Fourier domain

疏信号s，然后可以使用设计好的观测矩阵Φ对稀疏信号s进行稀疏采样，得到观测值y.最后，利用图像重建算法可以将观测值y恢复成完整的重建图像信号x′.

傅里叶域稀疏采样所用观测矩阵根据不同的采样模式设计而成，每种采样模式都对应有专门的观测矩阵。随机笛卡尔采样和随机点采样方便简单且具有很强的随机性，这两种采样模式的观测矩阵十分容易满足与稀疏矩阵之间的RIP条件；螺旋采样模式一般以阿基米德螺旋(Archimedean spiral)作为采样轨迹，该方法对于动态场景具有较好的成像效果；星型采样和双星型采样相比其他采样模式，更加注重对原始图像在傅里叶域中心位置聚集的大量低频数据进行采集，其在傅里叶域中心区域的采样面积远大于周边其他区域。考虑到一般情况下自然图像其傅里叶域上的数据分布也是聚集在图像中心，所以这两种采样模式对于一般自然图像的采样效果略高于其他模式。特别是双星型采样模式，其中心位置的采样密度更高，在低采样度的情况下，双星型采样有更大可能采集到稀疏数据，所以这种采样方式在低采样率情况下会有更好的效果。

1.4 图像重建

在确定了图像信号的稀疏方法和采样模式后，便可以对图像在稀疏变换域上进行压缩采样。对于自然图像信号x，可以利用观测矩阵Φ对x进行采样得到测量值为y，对稀疏信号x的重构过程可以根据式(3)的方法表述为L0范数最小化问题：

(10)

式中：L0范数指矩阵中非0的元素个数，通过对L0范数的计算可以有效反映出矩阵的稀疏程度。假设存在有矩阵C，它的L0范数可以通过式(11)来表示。

(11)

然而，L0范数最小化问题是一个NP-hard问题，计算过程复杂且计算量大，在数据维度较大时，计算效率低下。可以对该问题进行凸优化，利用L1范数来代替L0范数，通过求解基追踪问题来获取L0最小化问题的近似解[13]。

2 基于稀疏采样的图像压缩算法

2.1 观测矩阵序列的构建

传统图像压缩方法一般通过对图像数据的计算和分析，找出图像信息中的冗余数据，通过丢弃冗余信息的方式达到压缩图像的目的。然而，求出冗余信息的计算过程往往具有一定的复杂性，对于能量、计算、存储性能受限的无线多媒体传感器网络节点而言负担较大。压缩感知方法则与传统图像压缩方式不同，它可以利用构筑好的观测矩阵对原始图像进行直接压缩采样，其采样过程实现了对图像信息的压缩，因此对于节点计算性能的要求大大降低。根据图像在稀疏变换域上的数据分布，设计合适的观测矩阵，不但可以降低节点的数据处理能耗，还可以有效保证重建图像的视觉质量。

经过傅里叶变换的图像，其中心部分聚集有大量的低频数据，这些数据使图像成分变得易于采样，也使基于傅里叶域的压缩采样成为可能。本文针对这一特性，结合了星型采样模式和双星型采样模式，设计观测矩阵构筑方法。通过生成一组观测矩阵序列(其中包含了各个采样率的观测矩阵)，可以很好地满足不同采样度下的采样需求。采样矩阵一般情况下使用星型采样模式，以均匀分布的采样轨迹进行采样，可以适应于任意自然图像。在低采样率的情况下，使用双星型采样模式进行采样，从而保证图像的重构效果。

2.2 傅里叶域稀疏采样的图像压缩方法

对于尺寸较大的图像，分块处理是最常用的图像处理手段。对大尺寸图像进行块状分割并分发给各个节点进行处理，不仅可以利用并行处理大幅减少单幅图像所花费的时间，而且还能够有效降低单个节点的数据处理能耗。就观测矩阵构筑方面而言，采用分块处理可以有效减小观测矩阵，从而降低WMSNs节点的存储空间成本。本文提出的分布式自适应图像压缩方法将对采集到的原始图像进行块状分割，并以分布式多点协作的方式在傅里叶域对其进行稀疏采样。

自适应图像压缩根据图像不同区域的构成复杂度来分别匹配不同的采样率，从而尽可能提高图像的整体质量，常用的衡量图像构成复杂度的标准包括方差、图像边缘算子等。其中，方差作为图像变化剧烈程度的直观表现，在一定程度上可以反映出图像构成的复杂度。同时，和其他衡量方法相比，方差更容易计算且计算能耗非常低，因此图像压缩方法将各个块状图像各自的方差值作为衡量其信息复杂度的标准，并以此为基准实现图像的分块自适应压缩。算法描述如下。

算法1：图像分块自适应压缩采样算法

Input：原始图像矩阵P，平均采样率R，分块大小p,q.

Output：块状图像的压缩数据D，观测矩阵编号n.

(1) [h,w]=size [P];

(2)a=h/p,b=w/q,s=0,t=0;

(3) fori=1 toa

(4) forj=1 tob

(5)t=t+1; ∥对原始图像进行块分割

(6)G{t}=P((i-1)×p+1:i×p,(j-1)×q+1:j×q);

(7)v(t)=var(G{t}(:)); ∥求矩阵方差值

(8)s=s+v(t);

(9) end for

(10) end for

(11)d=0.35+R×0.65; ∥设置基础采样率

(12) fori=1 tot

(13)r=d+16×v(t)×(1-d)/s; ∥计算自适应采样度

(14)n(i)=round(r×100); ∥匹配观测矩阵编号

(15) end for

(16)D=Compressive sampling (G,n)

(17) 输出压缩数据D和对应的观测矩阵编号n.

假设原始图像大小h×w，并按照p×q大小进行块状分割。在压缩端执行的图像分块自适应压缩采样过程可利用算法1进行详细表述。其中，算法1步骤(16)涉及的压缩采样过程由多个普通节点协作完成，其处理过程为：普通协作节点从原始灰度图像分割出的块状图像矩阵G{t}，观测矩阵编号n(t)；载入观测矩阵序列，对块状图像G{t}进行快速傅里叶变换，得到矩阵F=fftshift(fft(G{t}))；从观测矩阵序列中提取观测矩阵W=M{n(t)}；在傅里叶变换域上对块状图像压缩采样B=F×W；提取并保存块状图像的压缩数据D{t}=B(find(W!=0))；输出压缩数据D{t}和对应的观测矩阵编号n(t).

对块状图像进行自适应压缩采样后，整体图像的实际采样率为：

(12)

2.3 图像重建方法

在网络处于工作状态期间，基站或汇聚节点与传感器簇头节点进行通信并接收来自簇头节点压缩后的图像数据。基站或汇聚节点会首先根据接收到的观测矩阵编号，从观测矩阵序列中提取相应的观测矩阵，然后根据观测矩阵将压缩数据恢复到欠采样图像矩阵状态。最后，利用非线性共轭梯度迭代将欠采样的观测矩阵进行恢复。

3 实验与结果分析

通过仿真实验对本文提出的稀疏采样多媒体传感网图像压缩算法进行图像重建多模式评估和图像恢复质量的对比分析。在现有公开数字图像上，首先进行自适应和非自适应采样模式的图像质量分析，随后与现有分布式图像压缩算法进行对比实验和分析，验证了本文提出算法的有效性。

3.1 不同采样模式下图像重建质量分析

图像重建质量的高低是衡量WMSNs图像压缩算法的重要指标之一，本节将通过实验证明本文所提出的分块自适应图像压缩算法完全可以满足实际应用场景下的图像质量要求。首先，按照以下三种不同的稀疏采样模式对尺寸为512×512的灰度图像进行压缩处理。

模式一：整帧直接压缩方法，即不进行分块，直接对整帧图像进行压缩。

模式二：分块直接压缩方法，先对整帧图像进行分块处理，然后分别对各个图像块进行直接压缩，各块图像的采样率均与模式一相同。

模式三：采用本文提出的用分块自适应压缩方法，先对整帧图像进行分块处理，然后根据每块图像各自的方差进行自适应采样率分配。各块图像的采样率虽各不相同，但整个图像的总体采样率与模式一和模式二保持一致。

为了保证测试结果具有普遍性，分别以Lena、Peppers、Baboon三幅图像作为测试样本，在不同综合采样率下对算法的重构效果进行了统计，具体结果如表1所示。

表1 不同采样模式下重建图像的PSNR值Table 1 PSNR values of reconstructed images in different sampling modes dB

通过表1的实验对比结果可以看出，使用本文提出的分布式分块自适应压缩采样模式重建出的图像PSNR更高，表明本文提出的算法模式具有明显的优势。

3.2 与现有其他分布式图像压缩算法对比

将本文提出的算法与BSC-SPL[11]、STD-BCS-SPL[12]和SVD[10]算法进行相同采样率或压缩率的图像恢复质量对比分析。对比结果如图3-5所示，分别在lena、Barbara 2、Boat图像上的实验对比结果。

图3 Lena图像重建后的PSNR对比结果Fig.3 PSNR comparison of the results of recovered Lena image

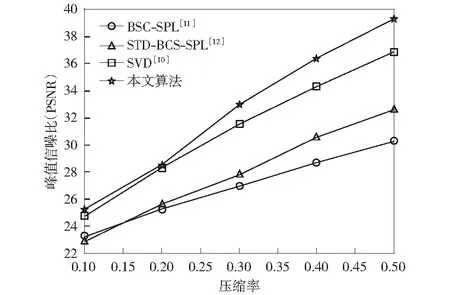
图4 Barbara2图像重建后的PSNR对比结果Fig.4 PSNR comparison of the results of recovered Barbara2 image

从图3-图5的对比中可以看出，本文提出的基于傅里叶域稀疏采样的分布式多媒体传感网图像压缩算法，通过自适应地选择观测矩阵，在图像压缩采集和恢复性能上具有一定的稳定性；另外虽然有些情况下SVD算法与本文算法比较相近，但是SVD算法需要进行矩阵分解，其编码端复杂度要高很多，因此本文提出的采集压缩算法要更适合于多媒体传感网应用场合。

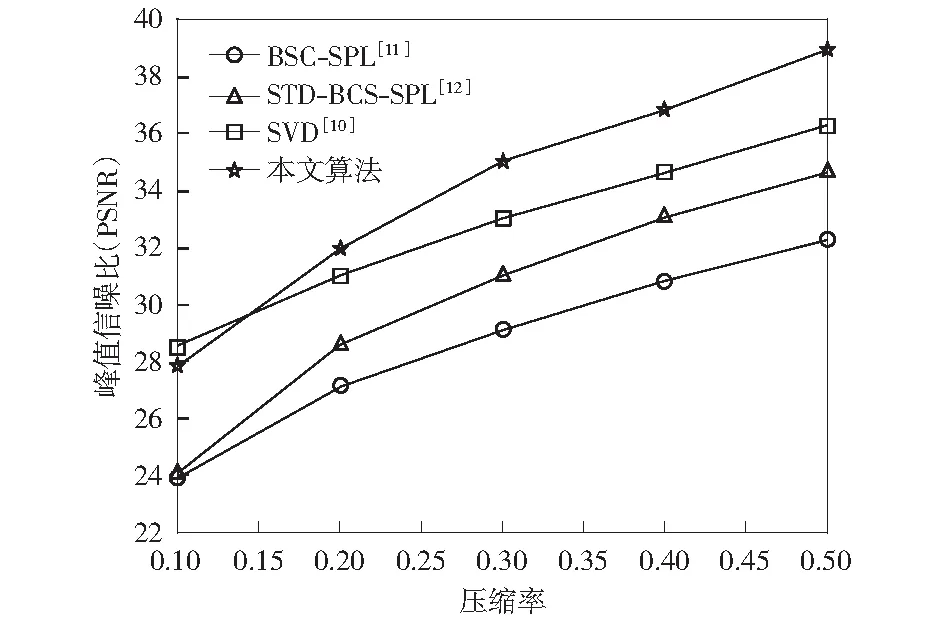
图5 Boat图像重建后的PSNR对比结果Fig.5 PSNR comparison of the results of recovered Boat image

4 结束语

有限的能量供应是无线多媒体传感网被大规模推广应用的瓶颈之一。本文针对无线多媒体传感器网络的低能耗图像压缩和传输问题，综合了分布式处理思想和稀疏采样理论，提出了一种基于傅里叶域稀疏采样的的分布式图像压缩方案。该方案通过将图像转换到傅里叶域进行分块自适应压缩采样与传输，通过对公开图片数据集和现有算法的对比，验证了本文提出算法的有效性。本文中提出的图像压缩方法遵循“轻编码，重解码”的理念，可以使用不同类型的节点来分摊图像处理工作，符合WMSNs的设计特征。