基于文本数据挖掘的复杂工况螺纹连接力矩衰减预测方法
2021-01-21王昌健蒋国璋段现银
王昌健,蒋国璋,段现银
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学 机械传动和制造工程湖北省重点实验室,湖北 武汉 430081)
0 引 言
螺纹连接件由于拆装简便、可靠性强、成本低、互换性好等特点,被广泛使用于各类机械设备中。但是,螺纹连接力矩不可避免会随着服役时间增加而逐渐衰减,使连接件发生松动,甚至断裂,轻则产生偏载、异响,重则导致重大安全事故。以重型卡车推力杆螺纹连接为例,由于其服役于交变横向载荷和横向振动等复杂工况中,更容易发生失效和造成严重损失。为排查机械设备螺纹连接的安全隐患,以提高机械设备工作的可靠性,很有必要对该类螺纹连接的力矩衰减进行有效预测。国内外学者及研究机构针对复杂工况螺纹连接力矩衰减问题进行了大量研究工作。
对于螺纹连接的失效及力矩衰减问题,传统解决方案一般是以实验和仿真的方法分析力矩衰减。在仿真方面,巩浩等[1]通过多种有限元模型仿真对比,揭示了横向振动条件下的预紧力衰退机理,发现应力再分布是导致预紧力衰退的一个重要原因,并在此基础上系统地分析了在不同条件下预紧力衰退过程的规律;刘传波等[2]分析了螺纹紧固件防松机理,同时建立了螺纹连接拧紧扭矩计算模型,针对有效力矩型锁紧螺母计算模型进行修正,并对修正模型计算的可靠性进行了实验验证。在实验方面,邵国强等[3]开发了一种高精度螺栓装配连接实验平台,模拟不同材料和规格的螺栓装配过程,系统研究了被连接件材料、螺栓等级等6个因素与扭矩-预紧力的关系,得出表面粗糙度和被连接件材料为扭矩系数的显著影响因子,从而指导优化了螺栓装配工艺;针对复杂工况下的螺纹连接失效问题,李海波等[4]通过对重型卡车钢板弹簧骑马螺栓进行实验受力和力矩衰减机理分析,指出钢板弹簧与板弹簧座间的间隙以及弹簧各片间的内摩擦是导致钢板弹簧骑马螺栓力矩衰减的主要原因,并给出了改进方案。
以上研究在螺纹连接的衰退机理、影响因素和防松策略等方面都取得了较好的进展,但实验方法一般成本较高、周期较长;仿真方法则存在仿真模型的精度与稳定性无法保证的问题。总体而言,通过设计实验及仿真,控制单一特征的传统解决方法不能有效地从宏观上发掘主要影响因素。另一方面,基于数据的机械故障预测已经越来越广泛地应用于各行各业,但对于螺纹连接的力矩衰减预测的研究却少有报道。
在故障预测领域,随着数据监测与处理技术的不断发展,数据驱动的工业设备关键部件故障预测领域积累了丰富的理论与方法进展,如随机森林[5](RF)、人工神经网络[6-8](ANN)和贝叶斯信念网络[9](BBN)等。温江涛等[5]利用随机森林算法对模糊粒化后的旋转机械故障特征进行融合分类,提高了故障诊断效率;HUANG R等[8]以轴承退化期为研究对象,首先利用自组织映射神经网络生成最小量化误差训练BP神经网络,然后通过失效权重适用技术构建了剩余寿命预测模型;ZHANG X等[9]提出一种利用高斯混合贝叶斯置信网络识别轴承退化状态,由退化状态识别结果随时间的变化预测剩余寿命的方法。
上述研究成果将数据挖掘技术的理论与方法应用于各种机械设备故障预测,而复杂工况下螺纹连接力矩衰减问题区别于普通机械设备故障,它具有力矩衰减数据不易获取、特征数量和规范性不足等特点。导致上述常用方法在螺纹连接的力矩衰减预测中容易出现过拟合,预测结果难以满足精度要求等。因此,有必要研究针对螺纹连接力矩衰减预测的特点与难点的预测方法。本文提出基于数据挖掘的复杂工况螺纹连接力矩衰减预测方法,开展复杂工况下螺纹连接力矩衰减的回归预测。将随机森林算法与岭回归预测算法进行Stacking集成,利用2种不同结构与原理算法的互补优势,解决在单一算法模型下容易过拟合的问题,减小力矩衰减预测模型的预测偏差与预测方差,并将该方法应用于大型商用车生产企业D的故障数据库,进行实例验证与分析研究。
1 基于文本数据挖掘的故障量化方法
文本极性分析是文本数据挖掘技术中应用最广的分支,文本极性分析也称为文本情感倾向性分析,主要是对文本数据中所包含的意见、观点和情感等,进行挖掘、分析、归纳和总结,最后得出整个文本的极性倾向。文本极性分析方法主要分为基于机器学习的方法和基于词典的方法,基于机器学习的方法需要大规模经人工标注的训练集,且容易忽视文本语句的结构变化,基于词典的方法原理简单,但存在通用极性词典无法适用于专业性较强领域的问题。为了综合提高文本极性分析的效率和准确性,考虑导致极性变化的特殊语言结构,本文提出一种基于专业领域词典的规则化故障量化方法。
1.1 量化方法框架
以汽车行业为例,汽车制造企业在生产、销售及售后维修过程中,常常无法对汽车已经出现的故障进行精确量化的测量与评价,因此,对于故障的描述一般只能通过文本和图像等非结构化数据的形式保存。其中,汽车售后故障鉴定文本作为鉴定汽车售后故障等级、评判售后赔偿金额的原始记录和直接依据,蕴含着丰富的信息。故对故障描述文本进行深度挖掘,建立文字描述与故障等级所具有的一般映射关系具有重要意义。
针对复杂工况螺纹连接力矩衰减问题,构建使用于其专业领域的极性词典。考虑会影响文本极性变化的特殊语言结构,运用文本极性分析方法对螺纹连接力矩衰减故障进行量化评级。量化方法框架如图1所示,挖掘流程概括如下。
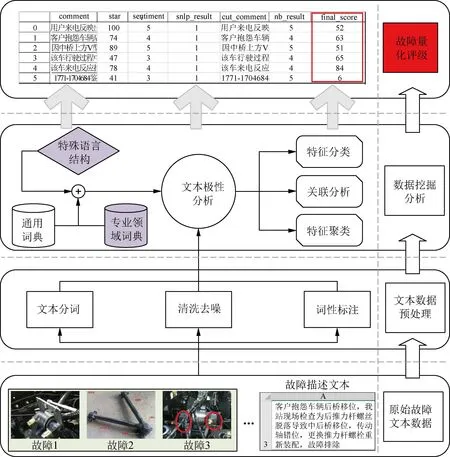
图1 基于数据挖掘的故障量化方法框架
步骤1 文本数据预处理。
针对原始故障描述文本数据,首先进行预处理,对文本进行清洗去噪、词性标注等工作,剔除文本中的无意义数据。
步骤2 数据挖掘分析。
基于所构建的专业领域极性词典和现有的通用词典,结合考虑特殊语言结构的极性分析规则,对经预处理后的文本数据进行挖掘分析。
步骤3 特征分析与获得量化结果。
针对步骤2所挖掘分析的结果,建立文本描述故障等级间的一般映射关系,获得故障量化评级。
1.2 基于词典的故障量化规则
词典提供了一个词语在极性上的先验知识,也就是该词语在大多数语境下的极性及其强度等信息。词典极性词的得分则是对词语极性倾向性程度相对合理的量化。经典的基于词典的极性分析方法通常用式(1)计算极性值,即对极性词得分进行累加,得到文本片段的整体极性倾向值[10]。
(1)
式中:PT(polarity tendency)为文本的极性倾向值;M为样本词数;score(termk)为第k个词在词典中的极性倾向值。
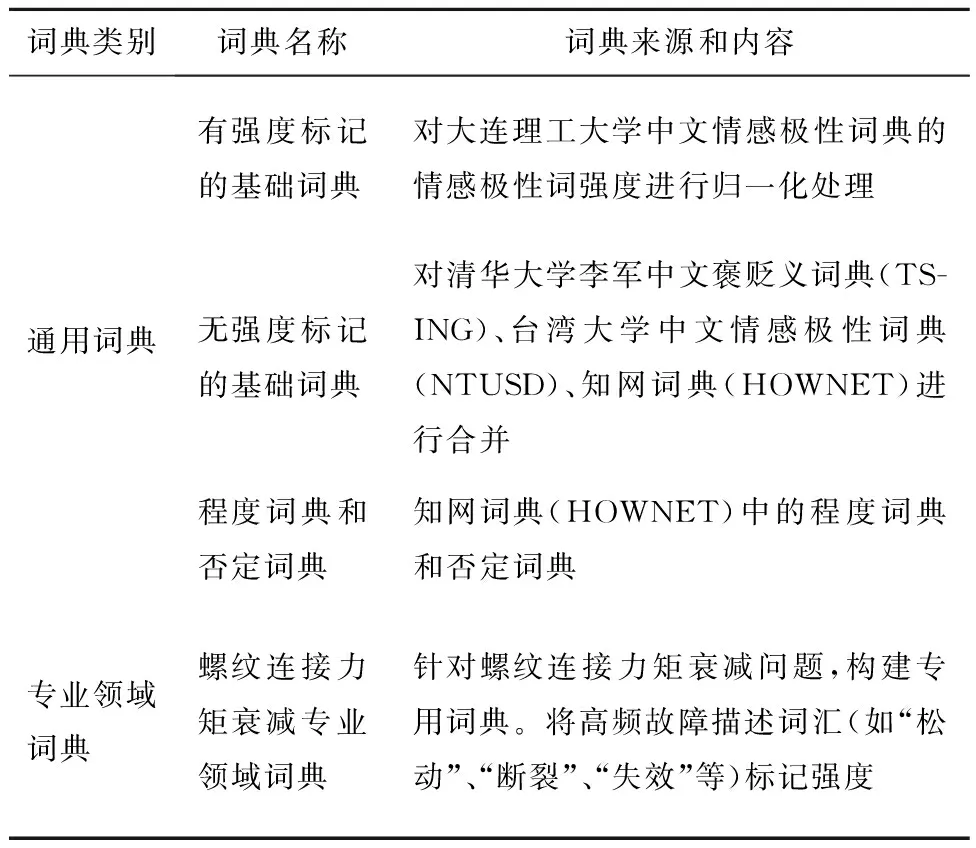
表1 故障量化词典
此方法忽略了导致极性变化的特殊语言结构,如否定、转折、情感极性强化和削弱等。本文考虑了导致词语极性变化的特殊语言结构,提出一种规则化故障量化分析方法。收集该方法所依赖的通用词典和所构建的专业领域词典(表1)。根据式(2)计算故障描述文本的极性量化值PQ(polarity quantization)。对故障文本中的字符串进行中文分词,按照预设的标点符号分割成N个子句单元;对每一个子句单元suk,使用cal_su_pq函数计算子句单元的su_pq;将N个su_pq相加,得到该条故障描述文本的极性量化值PQ,
(2)
Cal_su_pq算法如下。
输入:经过分词的故障文本子句字符串su。
在计算子句单元su_pq的过程中,考虑了中文表达的特点和语言极性表述的复杂性(如反意、虚拟等语义现象),设定3项细化的极性分析语义规则,如表2所示。
输出:子句的情感倾向性得分su_pq。
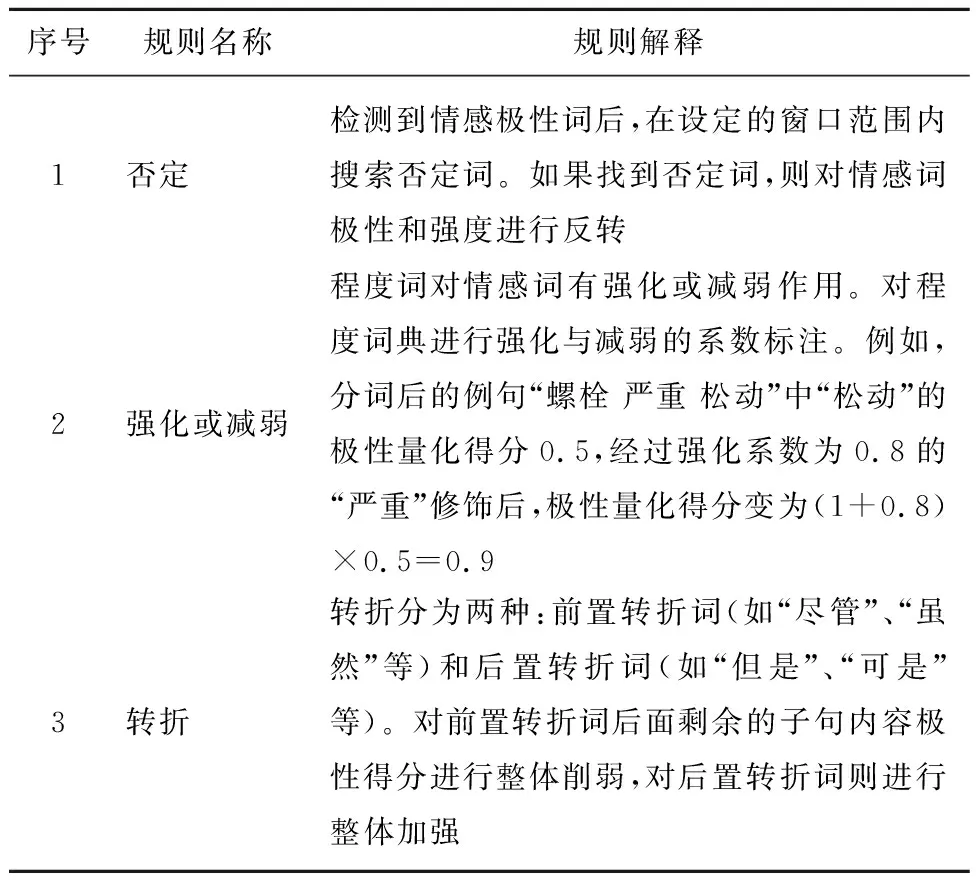
表2 故障量化分析语义规则
(1)初始化情感得分su_pq为0。
(2)将su按照空格解析为列表L,遍历L中的每一个词term。
(3)如果term是情感词,使用表2中的规则1和2,检测否定和加强(减弱)语义,将最终得分加入su_pq。
(4)如果term是转折词,递归计算剩余子句的得分,然后乘以转折变化系数后加上之前的得分,作为该子句的su_pq。
(5)返回su_pq。以某商用车制造企业D售后故障鉴定单中记录数据为例,分析两条与螺纹连接力矩衰减相关的故障描述,对故障进行量化,具体过程如图2所示。
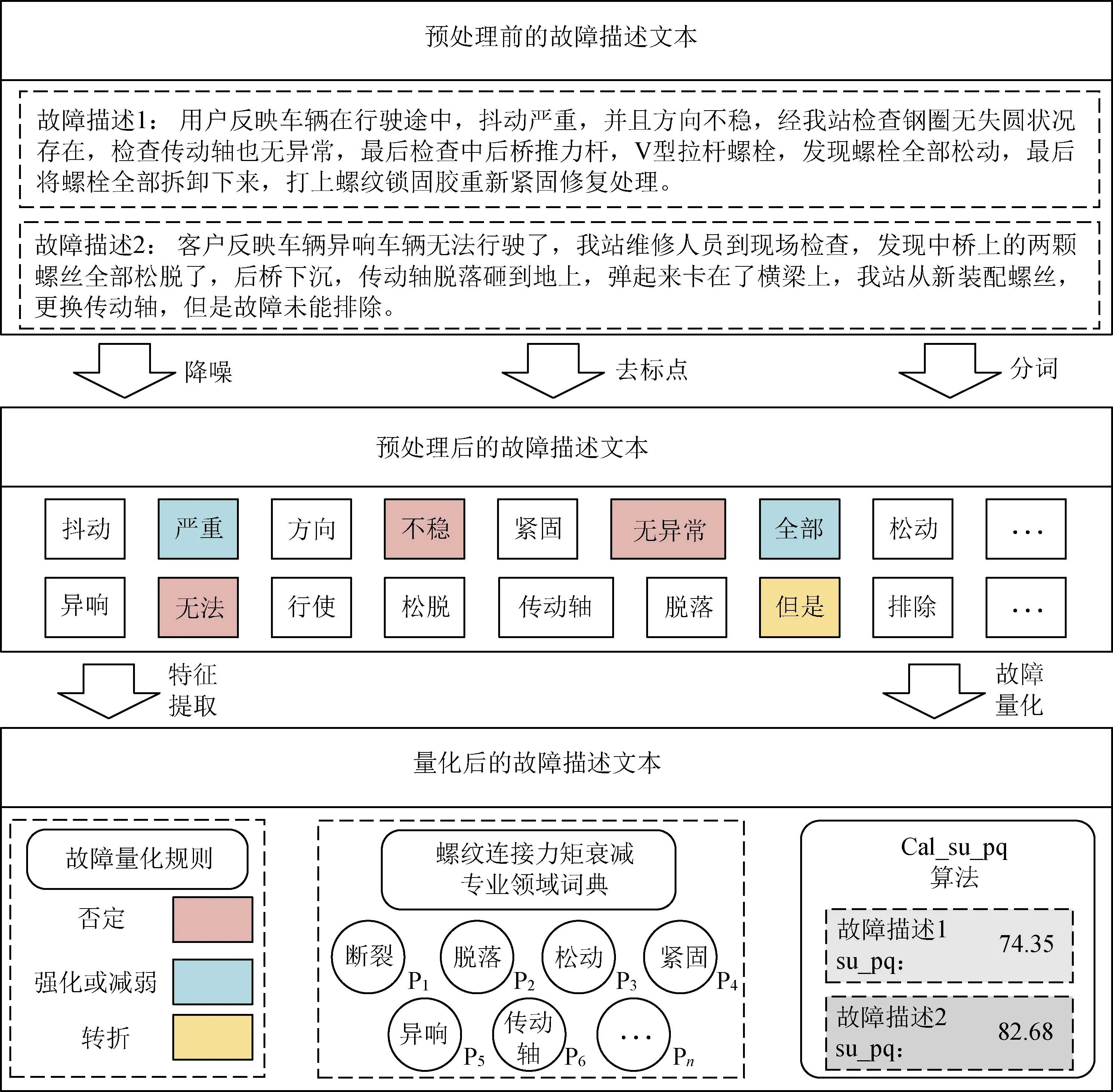
图2 螺纹连接力矩衰减故障量化流程
2 基于数据挖掘的螺纹连接力矩衰减预测建模
2.1 基于Logistic函数模型的力矩衰减相关特征构建方法
螺纹连接力矩衰减是一个强烈的状态非线性过程,该过程通常还伴有复杂的几何非线性(大位移)和材料非线性(塑性)影响,螺纹连接处于不同状态时,其松动机理也有明显的差别。已有研究表明[11],螺栓张紧力、工作载荷、工作温度、各结构形式与尺寸、结构材料和结构表面状态是螺纹连接松动的主要影响因素。
汽车制造企业依据这6大因素也不断地尝试从设计、制造(工艺)、管理3方面提出改进措施。依据多年实际生产经验,企业D针对重型卡车推力杆螺栓力矩衰减问题,陆续推行增加固体润滑剂、换用自锁型螺母、优化漆膜厚度和增加人工力矩检测工序等多项工艺与管理改进措施。生产过程中的各类工艺及管理相关因素与螺栓力矩衰减密切相关,挖掘分析两者间的关联,对螺纹连接力矩衰减相关特征集的构建具有较强的实际意义。
Logistic函数是一类用来描述持续过程的函数模型,由于充分考虑了内禀增长率和环境因素限制2方面因素,因此,在生态学、材料损伤演化和工程学等方面获得了广泛的应用[12],由缓慢的初始过程经历较为剧烈的中间过程,最终趋于极限或最佳效果。故Logistic函数的这种特性与汽车制造企业推行各项改进螺栓力矩衰减的措施后,逐步达到最佳改进效果的规律类似。函数式为
(3)
(4)
式中:ymax为最大值;y0为初始值;r为增长速率系数。
针对企业D已推行的各项工艺与管理改进措施,引入Logistic函数,以改进措施推行时间为自变量,建立螺栓力矩衰减改善效果映射关系。同时根据实际生产与管理经验,各类工艺改进措施的推行难度,实际效果差异明显,为了更切合实际地反映改进措施从推行到起效的过程,提出措施施行难度系数S,结合企业D工艺部门历年生产经验,赋予5大类7小项改进措施的S系数值,如表3所示。
根据公式(3)和(4)可得在Logistic模型下工艺等级评分的总表达式,如式(5)所示。
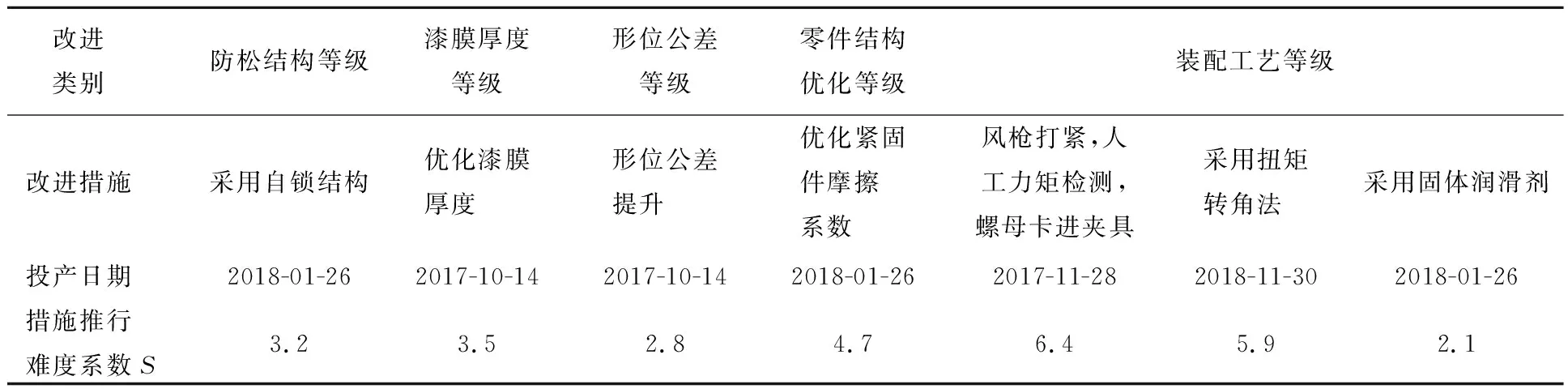
表3 改进措施施行难度系数
(5)
式中:G为工艺等级评分;Si为各项改进措施施行难度系数;ymax为Logistic模型下函数最大值;y0为初始值;r为增长速率;ti为各车辆故障时间;t0为改进措施上线投产时间。
2.2 基于岭回归和随机森林算法的Stacking集 成学习模型
Stacking集成学习通过组合多个异质基模型提升集成后的模型性能,相较于Bagging和Boosting的同质集成方式,Stacking集成学习从原理上更容易满足集成学习中“好而不同”的集成法则,实现互补优化[13]。
从数学角度而言,评价一个预测模型的性能,常以其泛化能力作为评价指标,模型的泛化误差则可以从模型的预测方差和预测偏差两方面来理解[14],如图3所示。
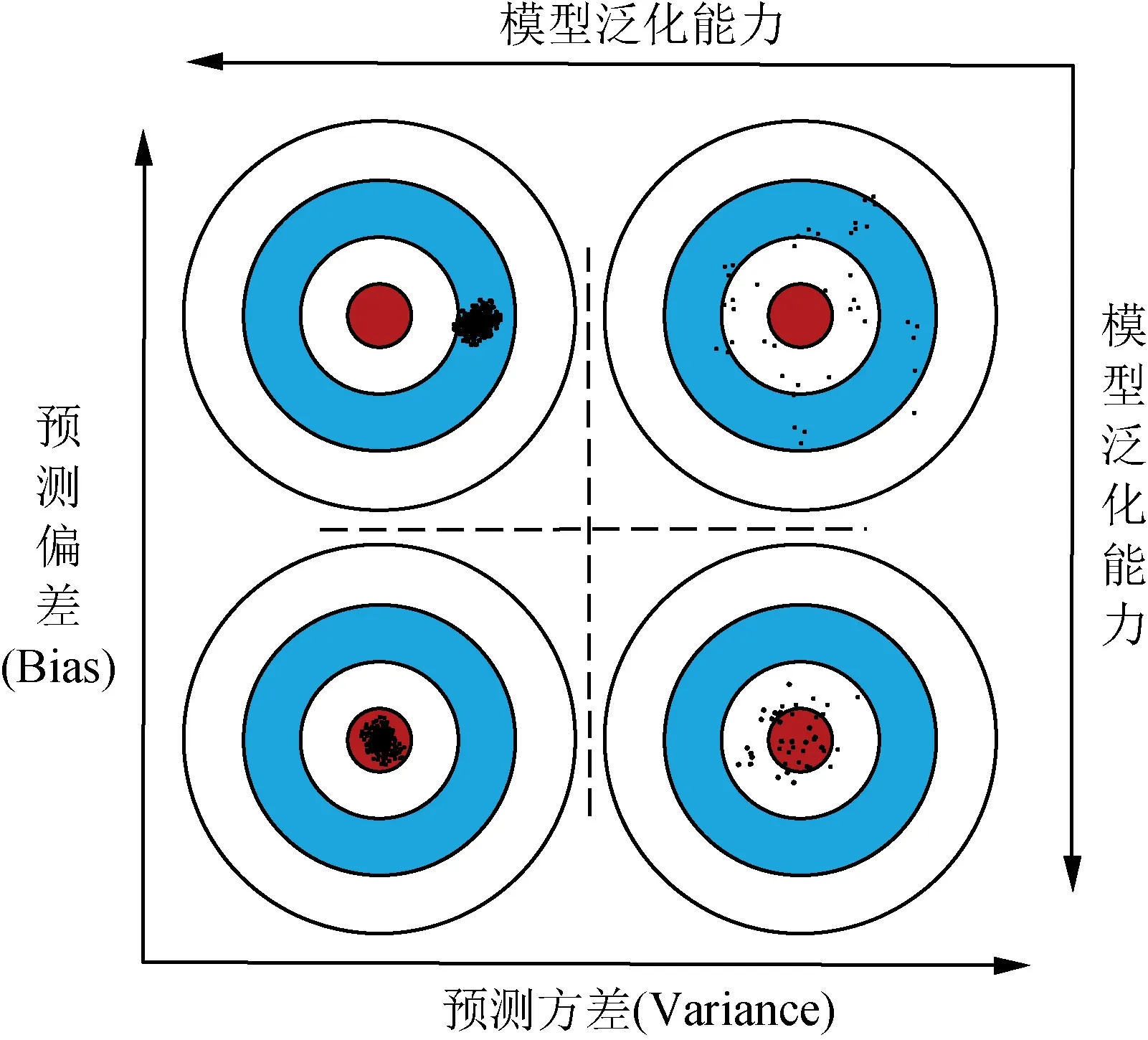
图3 预测偏差和预测方差
N个基模型fn组合得到集成模型F的过程中,预测偏差B(F)和预测方差Var(F)可表达为
[(N-1)·ρ+1],
(7)
式中:E[]为数学期望;F[X]为模型预测值;N为基学习器的个数;σ2,μ,γ,ρ分别为预测方差,预测偏差,基学习器被赋予的权重以及基学习器间的相关系数。
由式(6)~(7)可得,赋予预测性能较好的基模型更高的权重γ,降低基学习器之间的依赖关系(即减小ρ值)均可提升集成模型的泛化能力。
将不同的预测模型用Stacking集成方法进行集成的目的是提高整体预测的精度。Stacking集成中以L表示用于集成的基模型,数量记为N,分别为L1,L2,…,LN。各基模型对同一个数据集S进行预测,其中Si=(xi,yi),xi为解释变量,yi为被解释变量。通过基学习器产生的预测值为C1,C2,…,Cn,其中Ci=Li(S)。将第一层的输出结果作为第二层的输入,通过元学习器进行训练预测,得到最终的预测结果。
螺纹连接力矩衰减预测作为实际生产中的多元回归故障预测类问题,具有特征规范性不足,数据样本不易获取等特点。针对该问题,以随机森林和岭回归算法模型作为集成学习的基模型,其中随机森林算法对数据集的适应能力强,既能处理离散型数据,又能处理连续型数据,并且训练速度快,在各种回归问题上都具有较好的性能。岭回归算法对回归问题的处理效率高,且能弥补随机森林算法容易过拟合的缺陷。因此,以随机森林和岭回归算法作为Stacking集成的基模型,符合集成学习“好而不同”的集成原则。二级Stacking集成学习原理如图4所示。
以随机森林算法作为基学习器A,岭回归算法作为基学习器B,集成具体步骤如下。
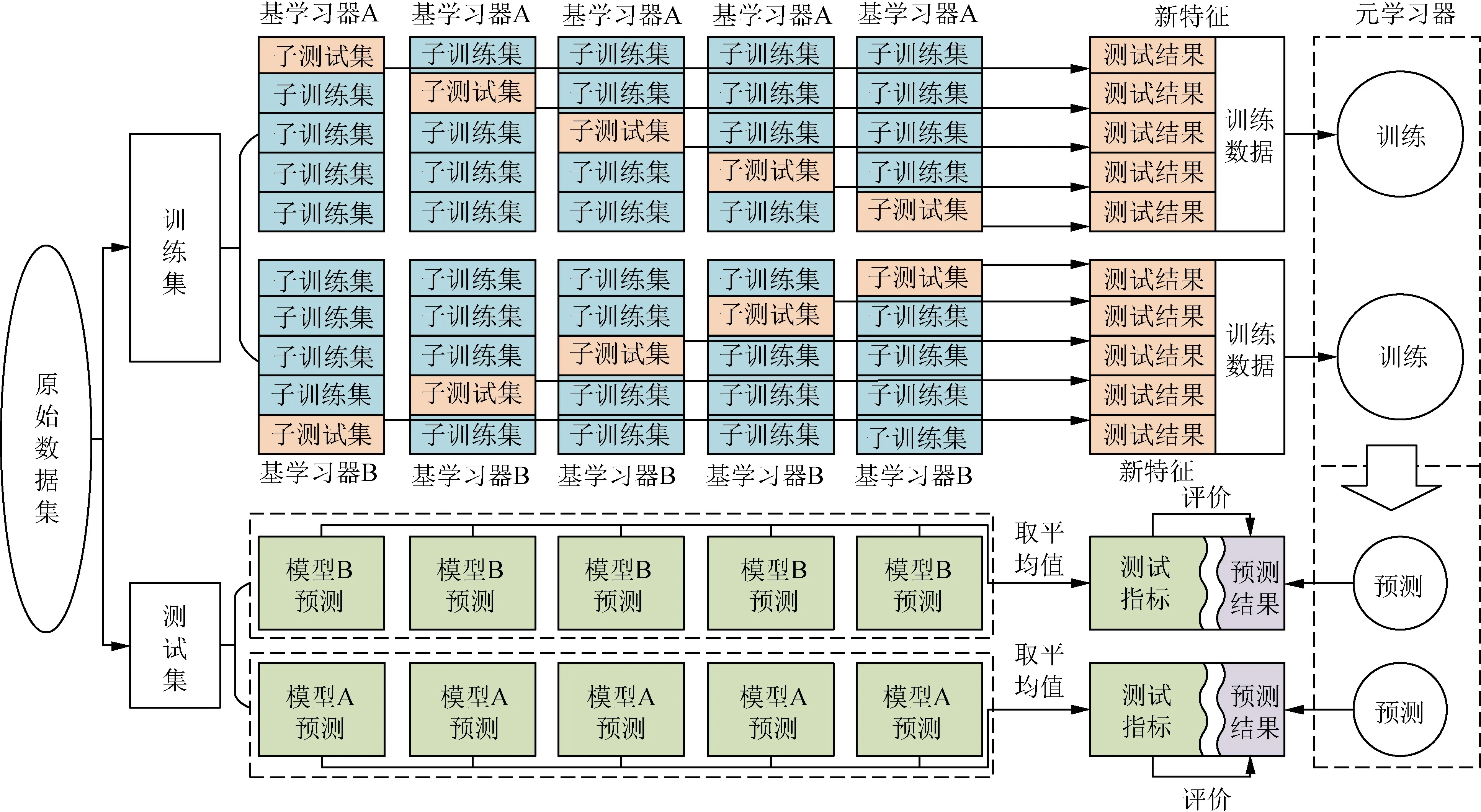
图4 二级Stacking集成学习原理
步骤1 数据集划分。
由于螺纹连接力矩衰减原始数据集样本体量不大,为了减小数据样本容量少造成的过拟合现象,对基学习器的训练集作K折划分,将训练集切分为K份,每一个基学习器每次取其中K-1份做为训练数据,另外一份作为测试数据,其中K选为5。
步骤2 模型训练。
将步骤1中基学习器5次测试得到的结果合并,作为元学习器新的训练数据输入元学习器进行学习训练。
步骤3 模型预测
基于测试集,综合各基学习器在每轮交叉验证中得到的预测结果,取其平均值作为元学习器的测试指标,最后利用不同基学习器得到的测试指标集对元模型进行检验和评价。
3 案例验证与分析
3.1 案例数据的特征相关分析
3.1.1 数据概况
以企业D生产销售的重型卡车力矩衰减相关案例为研究对象,提取2015—2019年售后故障鉴定单为数据样本集,各年各类故障记录多达8 000余例,各类故障中与螺栓力矩衰减相关案例占比高达41%。筛选出故障率最高、总赔偿金额最大的推力杆螺栓力矩衰减相关故障案例为研究对象。故障鉴定单中主要记录数据项目如表4所示,各类故障的占比情况如图5所示。
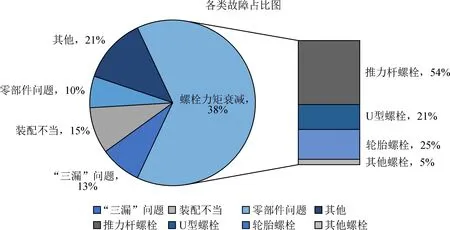
图5 各类故障占比图

表4 故障鉴定单关键数据
3.1.2 特征相关分析
进一步筛选2018年推力杆螺栓力矩衰减相关案例数据作为研究对象,考虑加入前文构造的5大工艺影响因素特征后,训练集共包含的特征数为15个,数据样本数为450个。
选用Pearson相关系数对15个特征进行相关分析,其相关系数介于[-1,1]间,2个特征间的相关关系是相互的,0表示不相关,1表示绝对相关,绝对值越大表示两者相关性越强[15]。
筛选出与螺栓力矩衰减程度相关系数最大的特征为:汽车行驶总里程、装配工艺等级、形位公差等级。其相关系数矩阵及散点图如图6所示。
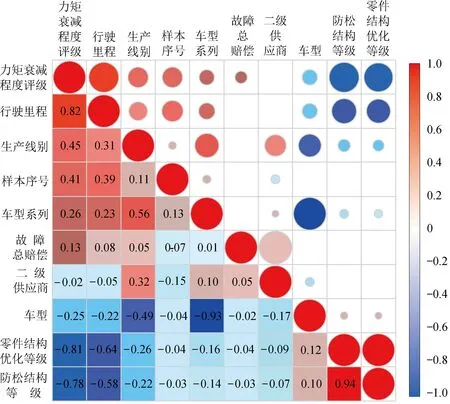
图6 特征相关系数矩阵Fig.6 Feature correlation coefficient matrix
3.2 样本数据清洗
3.2.1 缺失、异常数据处理
检查训练集中的缺失数据,对缺失数据进行平均值补偿。展示缺失数量前三的数据项,各项缺失数据个数均为0,结果表明,训练集数据完整度较高,如表5所示。

表5 数据缺失统计
异常数据处理,选取汽车行驶总里程特征作散点图,剔除异常数据点,id为58,315的异常点,如图7所示。
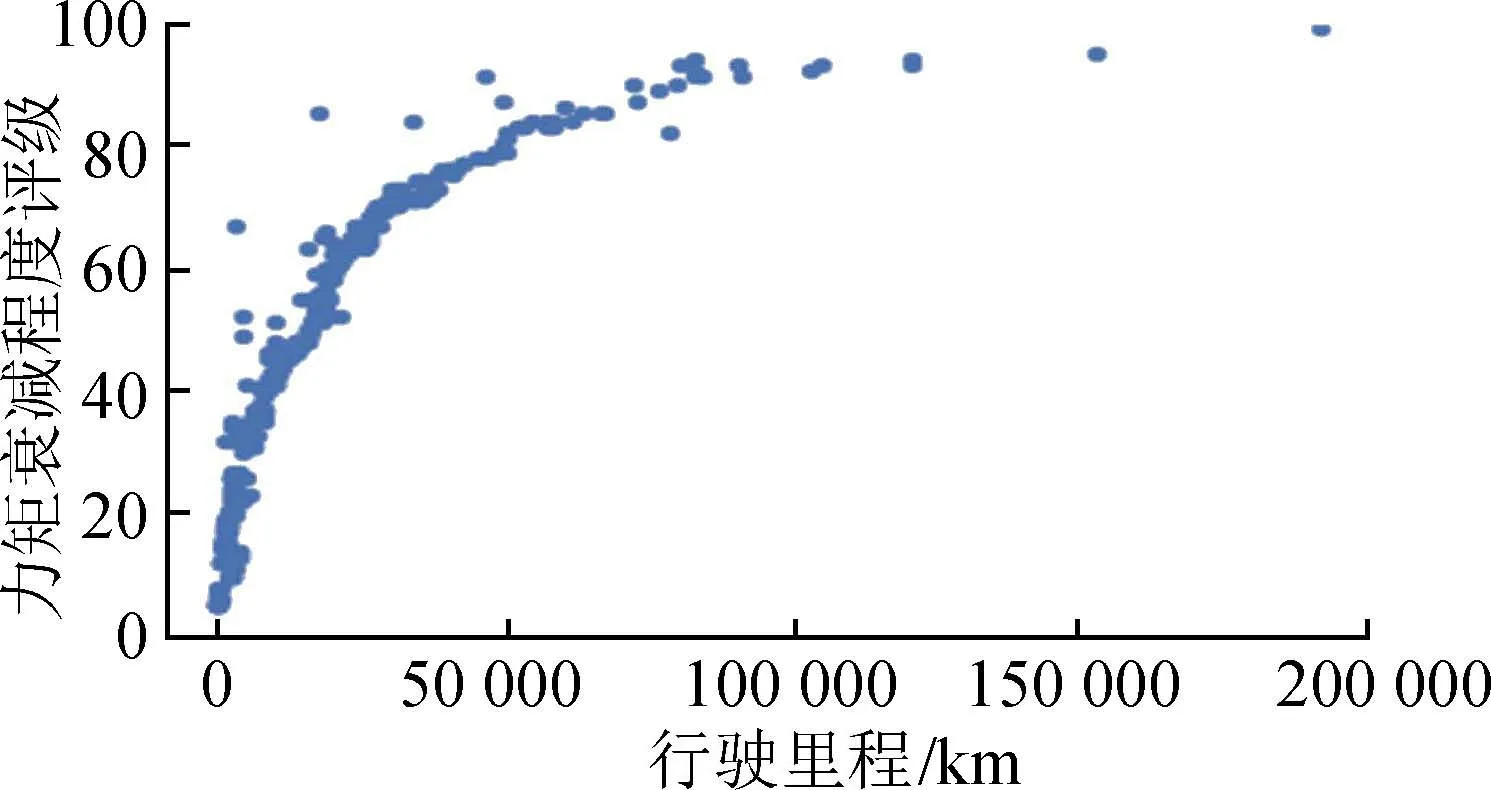
图7 异常数据散点图
3.2.2 数据One-hot处理及归一化
对类别型数据进行One-hot处理,消除类别
特征的数值影响。采用Python中pandas库自带的get_dummies方法实现One-hot。例如,重型卡车型号Model特征被分成12个column,每一个代表一个Category,是则赋值1,否则赋值0。
为了消除各项特征数据取值范围不同影响模型收敛的速度与精度,将各个特征数据进行归一化,降低模型线性回归效果不明显的现象。
3.3 预测结果与分析
3.3.1 岭回归模型预测
通过在损失函数中引入正则化项来达到降低回归过程的过拟合问题,拟定不同的50个参数,通过交叉验证选取最合适的参数,生成误差曲线如图8所示,当ɑ=0时,离散误差最小约0.40。
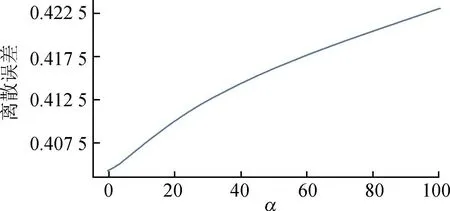
图8 岭回归模型预测误差曲线
3.3.2 随机森林模型预测
以随机森林中树木的颗数作为变量,设定子集0.3倍的特征数,来探索多少颗树木能达到最低误差,误差曲线如图9所示,当数目个数为200时,离散误差为0.24(最小)。
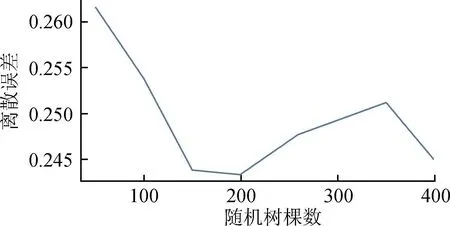
图9 随机森林模型预测误差曲线
3.3.3 基于Stacking集成学习模型预测
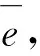
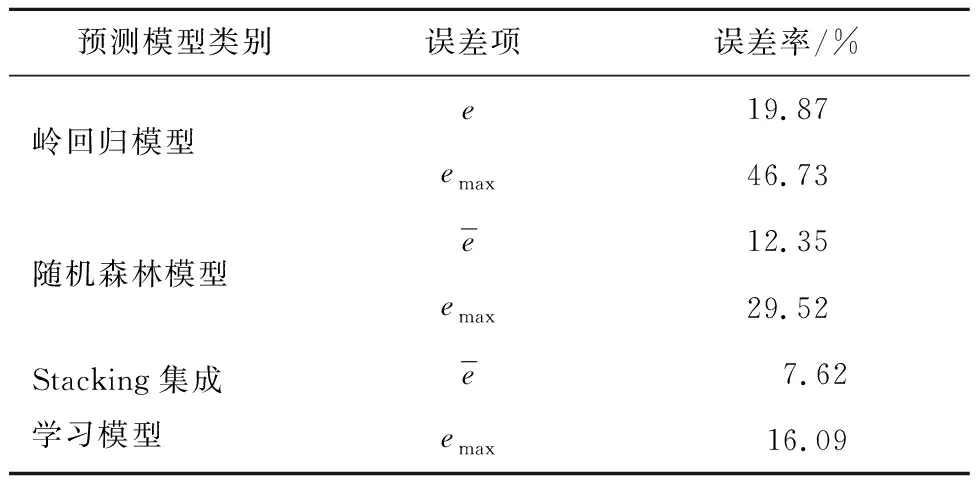
表6 各模型预测误差对比
从误差统计结果可知,Stacking集成学习模型比岭回归模型的预测平均误差减少了61.65%,最大相对误差减少了61.29%;比随机森林模型的平均误差减少了38.3%,最大相对误差减少了45.49%。
在特征数量和样本数量均有限的条件下,Stacking集成学习模型通过K折交叉验证,充分利用了训练数据,较单一预测模型准确率平均提升了53.39%,并有效改善了过拟合情况[[16]。
4 结 论
(1)建立了基于随机森林和岭回归算法的Stacking集成学习预测模型,解决了螺纹连接力矩衰减原始数据中小样本、特征不规范条件下回归预测模型严重过拟合问题,集成后的模型预测准确率较单一的随机森林和岭回归算法模型平均提升了53.39%。
(2)提出了一种有效的规则化故障量化分析方法,构建了螺纹连接力矩衰减专业领域词典与故障量化规则,对螺纹连接力矩衰减进行了基于文本描述的故障量化评级。
(3)以重型卡车推力杆螺栓力矩衰减预测为实际案例,构建了防松结构等级、漆膜厚度等级、形位公差等级、零件结构优化等级和装配工艺等级5类螺栓力矩衰减相关特征集,并进一步验证了基于数据挖掘的复杂工况螺纹连接力矩衰减预测方法的可行性。
