基于卡尔曼滤波的主子惯组匹配标定方法设计

李维刚，张鹏，李孟委,2,王树森

(1.中北大学 南通智能光机电研究院，江苏 南通 226000；2.中北大学 电子测试技术国家重点实验室，山西 太原 030051)

0 引 言

捷联惯性导航系统(strapdown inertial navigation system， SINS)将惯性测量组件(inertial measurement unit,IMU)与载体直接固连，仅利用IMU所感知到的载体比力及角速率信息就可为载体提供高精度的姿态信息，进而解算速度位置等导航参数[1]。该工作过程不受天气、磁力等外界干扰，也无需依靠卫星、中继等外界信息输入，具有自主性、无源性、体积小、抗干扰等优势,越来越广泛地应用于舰船、导弹、飞机等各种装备上，在民用和军事领域都发挥着愈发重要的作用[2]。

惯性测量组件作为测量载体姿态、位置、速度的敏感部件，是SINS的核心信息源，是惯性装备导航定位、精确制导、高效打击等关键技术的核心[3]。IMU关键指标的精确与否在很大程度上决定了SINS的导航精度。

对于安装在武器装备上的惯性测量组件，传统的周期性标定方法是拆卸以后运送到满足条件的实验室或仓库，利用高精度三轴转台进行分立式标定，对IMU的误差进行辨识。这样做对作战装备的机动性和实时性造成了比较大的掣肘，为解决这一问题，研究者提出引入外观测信息代替传统测试设备，实现外场标定。

杨晓霞等[4-6]在测试过程中引入了GPS、里程计和主惯组等外观测信息，无需测试转台,只要辅以车辆的不同机动方式就可利用Kalman滤波实现误差参数的标定；王乐[7]在仅引入主惯组信息的前提下设计了29维Kalman滤波器，通过编排导弹发射车的转弯、起竖和侧倾等机动，进行被测惯组的误差激励以实现免拆标定；王海亮等[8]利用炮车的常规机动方式在野战环境下实现了弹载IMU的简易标定。

以上研究者所做工作都实现了预期标定，但是存在滤波器维数过高、计算量大和载体运动路径过于理想化等问题。本文引入主惯组信息，设计12维卡尔曼滤波器，可在一定程度上补偿小型化可机动测试设备(350 mm×400 mm×500 mm，50 kg)的低控制精度，实现在低精度转台上的标定，具有一定的实用价值。

1 主子惯组匹配标定算法

目前，惯性测量组件的标定根据不同的输入基准可分为分立式标定和系统级标定。分立式标定以转台输入的角速率作为陀螺仪的基准，以角位置产生的重力加速度分量作为加速度计的基准，主要通过最小二乘法拟合输入矩阵与采样输出矩阵计算标定参数，其标定精度严重依赖于测试环境和测试设备精度；系统级标定从导航误差中推导IMU的标定误差模型，设计合适的转停方案激励被测件误差，再通过滤波算法逐步迭代校正标定模型参数[9]。系统级标定方法摆脱了对测试环境和设备的过度依赖，简化了测试流程[10]。

主子惯组匹配标定算法属于系统级标定方法，特别之处在于本方法以基准惯组和被测惯组导航参数之差作为观测量，通过卡尔曼滤波算法估计IMU误差项，然后将主惯组输出的加速度和角速率看作实际测量值，利用最小二乘法分离出子惯组中其余误差项。该方案的特点是：(1)摆脱了传统标定方法对测试环境和测试设备的苛刻要求；(2)测试过程中对外界环境干扰和测量噪声不敏感，从而提升了测量精度；(3)标定流程简单，易于实现。该方法适用于外场作战环境下对惯性装备中的捷联惯性测量装置进行标定和检测，同时也满足库存条件下惯性装备的定期维护需求。算法流程如图1所示。

1.1 误差模型建立

构建合理的误差模型是Kalman滤波器建立的先决条件，对陀螺仪和加速度计的误差产生机理进行分析并建立误差传递方程如下。

陀螺仪忽略随机干扰，误差模型为[11]

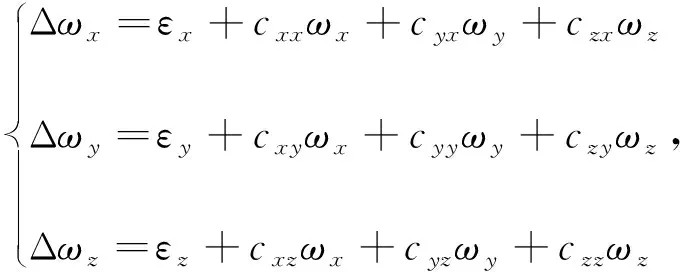
(1)

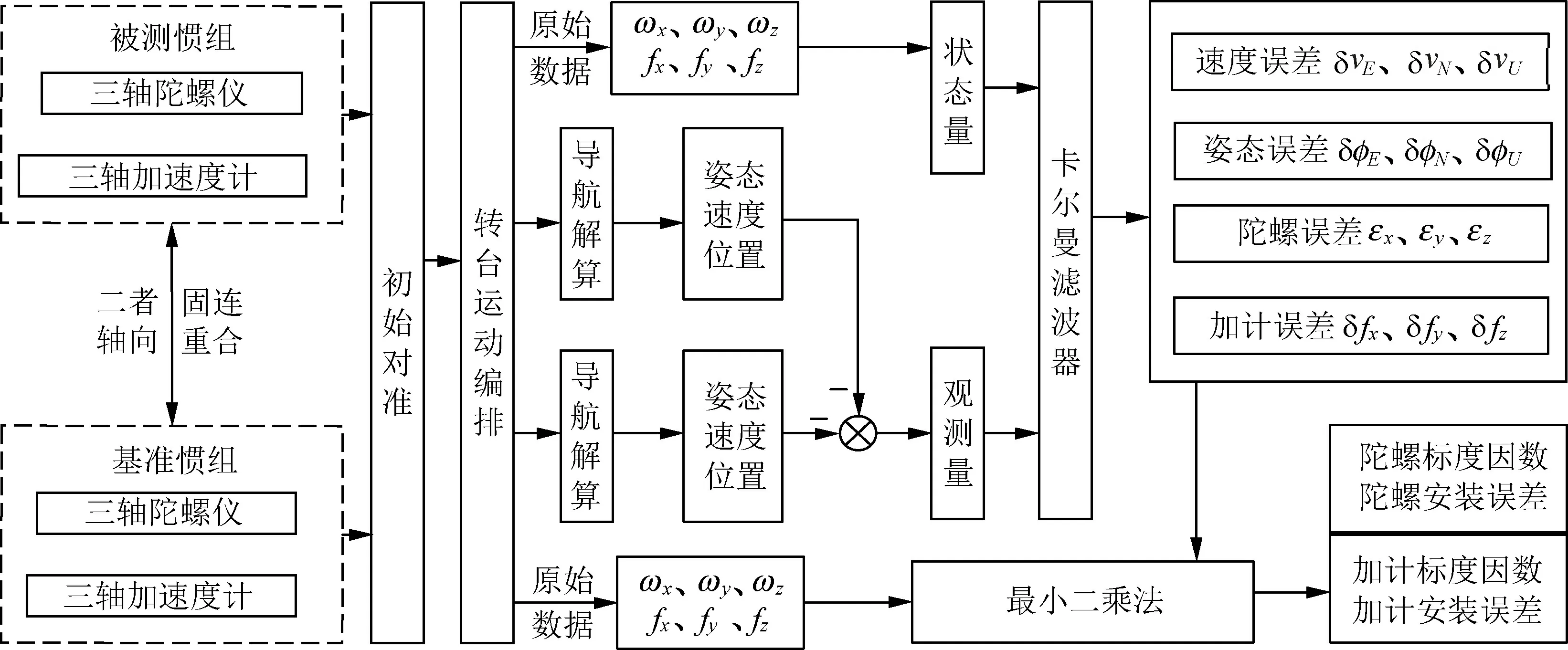
图1 主子惯组匹配标定算法流程图

加速度计忽略二次项误差，误差模型为

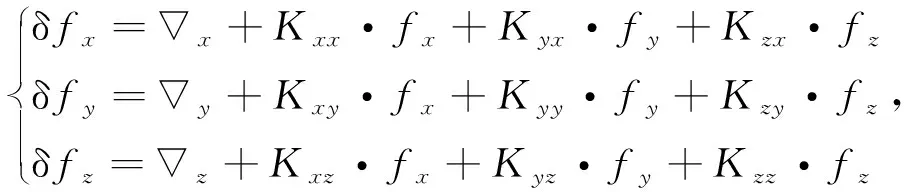
(2)

纬度误差

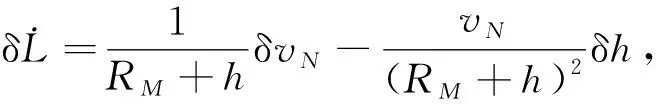
(3)

高度误差

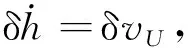
(4)

经度误差

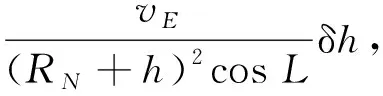
(5)

姿态误差模型为

速度误差模型为

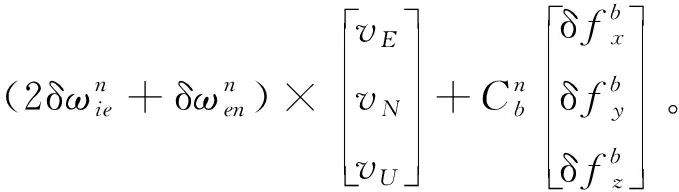
(7)

误差模型中各参数的涵义及其单位如表1所示，表1中δφE，δφN，δφU指子惯组东-北-天向姿态角相较于主惯组的误差。

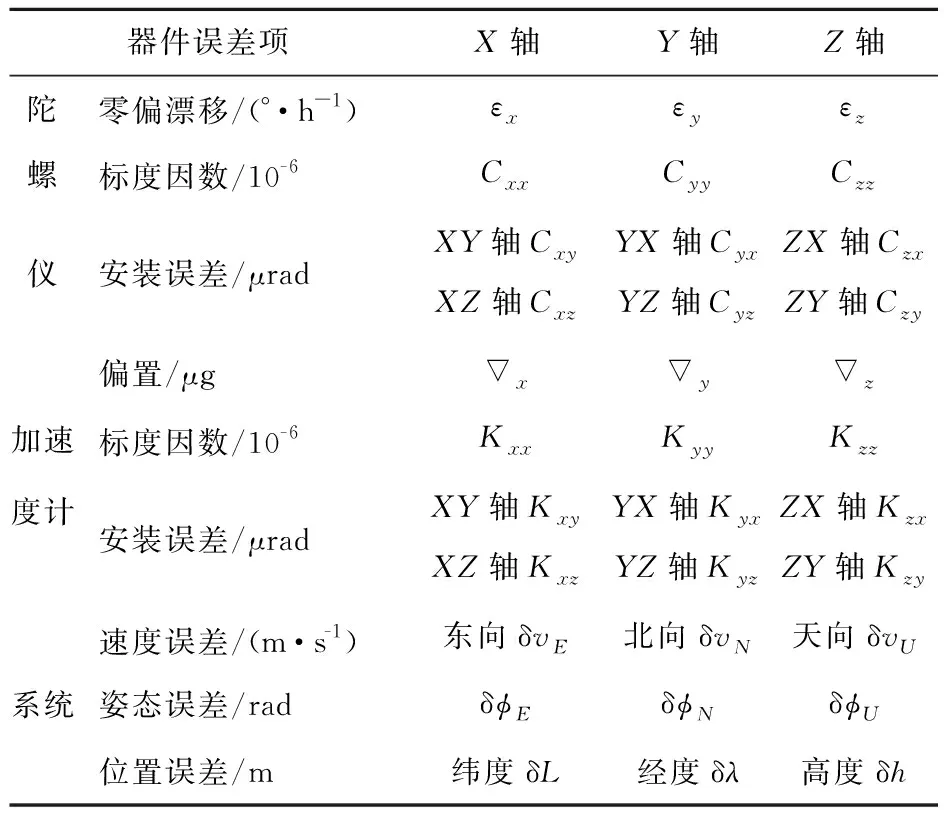
表1 误差参数明细

1.2 卡尔曼滤波器构建

卡尔曼滤波中,观测量为输入量，状态量为输出量。滤波器根据观测量修正状态量，进行迭代从而达到最优估计。卡尔曼滤波器是主子惯组匹配标定算法中最为重要的一部分，滤波器对采集到的IMU离散信号进行线性最优回归数据处理，通过观测量的不断修正，将误差模型参数迭代递推至最接近真实值的状态量[12]。

算法原理如图2所示。

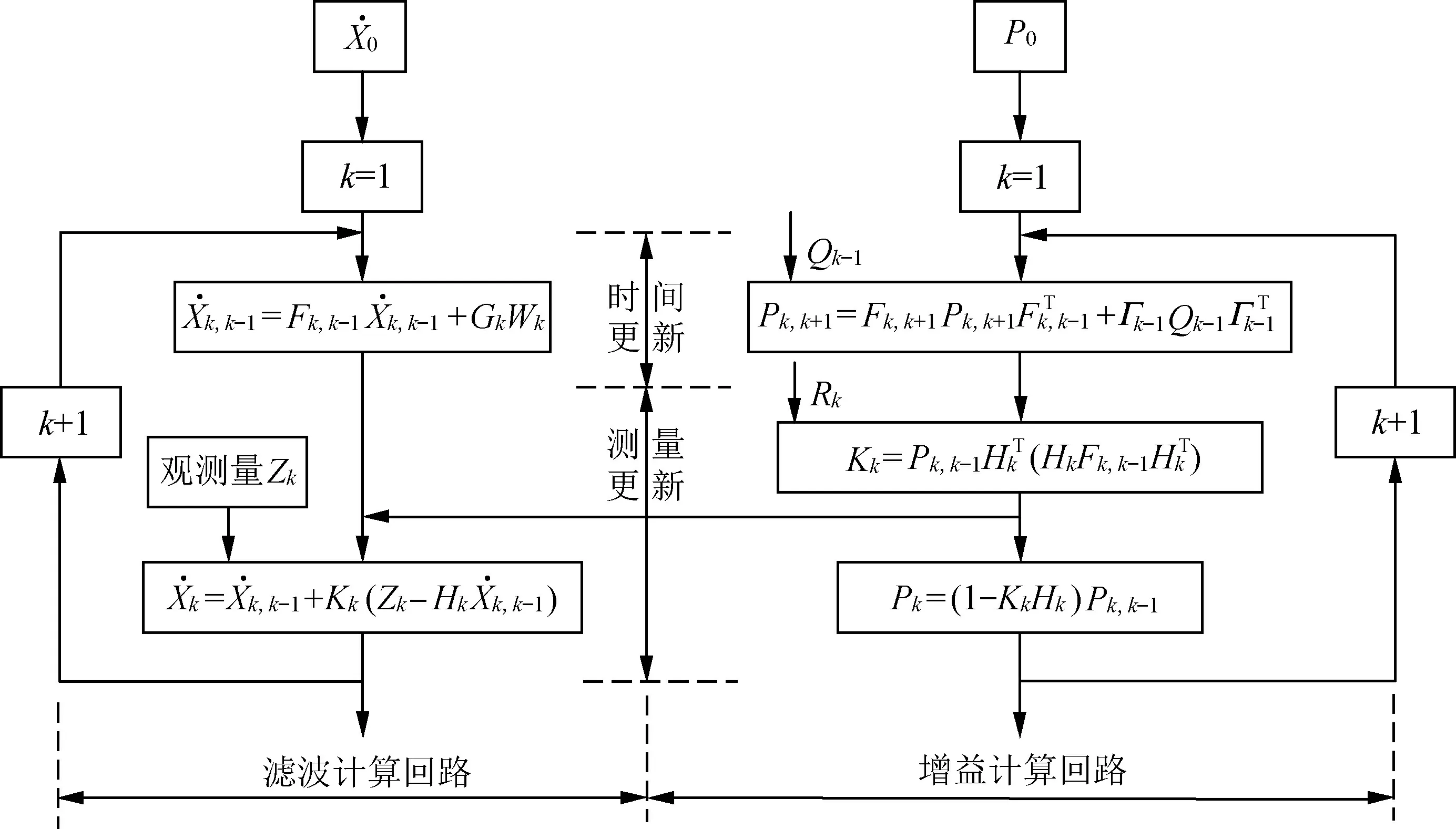
图2 卡尔曼滤波原理图

1.3 系统状态量选取

系统状态方程选用12阶卡尔曼滤波模型，包括三轴速度误差、姿态误差、陀螺误差和加速度计误差。其状态方程变量定义为

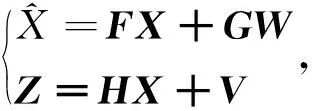
(8)

式中：

XT=[δvEδvNδvUδφEδφNδφUεx

εyεzXYZ]；

(9)

W=[WgxWgyWgzWaxWayWaz

0 0 0 0 0 0]T；

(10)

式中，V为量测噪声。

1.4 系统观测量选取

一般情况下，增加观测量可以加强系统的可观测性，提高系统的标定精度，捷联惯性测量单元测量的速度、姿态角、角速率、加速度、姿态矩阵等外部信息都可以利用[13]。但是加速度值受动态环境影响产生高频扰动，角速率积分会产生积分误差，这里都不予考虑。高动态环境下主惯导姿态是否可观测还有待研究；位置信息由速度信息积分得到，可观测性下降[14]。如何选取系统观测量，决定了标定系统的性能。

在传统的系统级标定算法中，整个标定过程不存在线运动，只存在角运动，若惯性器件为理想器件，则可以认为导航解算所得的速度为0，位置不变。因此,导航解算得到的速度与位置信息可以看作速度误差和位置误差[7]。在主子惯导匹配标定算法中，以基准惯组和被测惯组导航参数之差作为观测量。这样不仅可以提高观测量精度，而且能满足机动标定需求，还能降低动态干扰对标定结果的影响，满足外场标定的需求。

选用速度+姿态+位置匹配作为观测量时，由于主从惯组固连，轴向重合，二者的状态转移矩阵无限趋近于单位矩阵，因此可以认为二者在转台运动过程中的姿态角、速度、位置应完全一致。将主惯组的速度、姿态、位置作为基准，与从惯组的导航参数相减可看作更加准确的速度误差、姿态误差以及位置误差。将三轴9个误差项作为观测量，可得观测向量和观测方程为

Z=[δvEδvNδvUδφEδφNδφUδLδλδh]，

Z9×1=H9×12X12×1+V9×1，

(14)

式中,观测矩阵H为

其中，Ta为基准惯组测得的方向余弦矩阵。

选用速度+姿态匹配作为观测量时，观测向量与观测方程为

H=[δvEδvNδvUδφEδφNδφU]T

Z6×1=H6×12x12×1+v6×1，

(17)

观测矩阵为

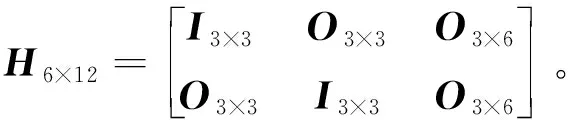
(18)

只选用速度作为观测量时，观测向量和观测方程为

Z=[δvEδvNδvU]T

Z3×1=H3×12X12×1+V3×1，

(19)

相应观测矩阵为

H=[O3×3I3O3×6]。

(20)

2 标定方法

根据上述系统级标定原理，设计标定方案。标定流程如下。

(1)将基准捷联惯性测量装置与待测惯组固连在三轴转台台面中心，轴向重合。

(2)以基准惯组的自身坐标系为参考坐标系，对被测惯组进行初始对准，保证其失准角非常小，即基准惯组与被测惯组之间的状态转移矩阵无限趋近于单位阵[15-16]。

(3)连接测试设备，给惯组供电并且预热，同时采集主、从惯组陀螺和加速度计的输出，等待测试设备与主、从惯组完成初始化。

(4)按照表2标定路径对三轴转台进行规定路径编排[11,17]。

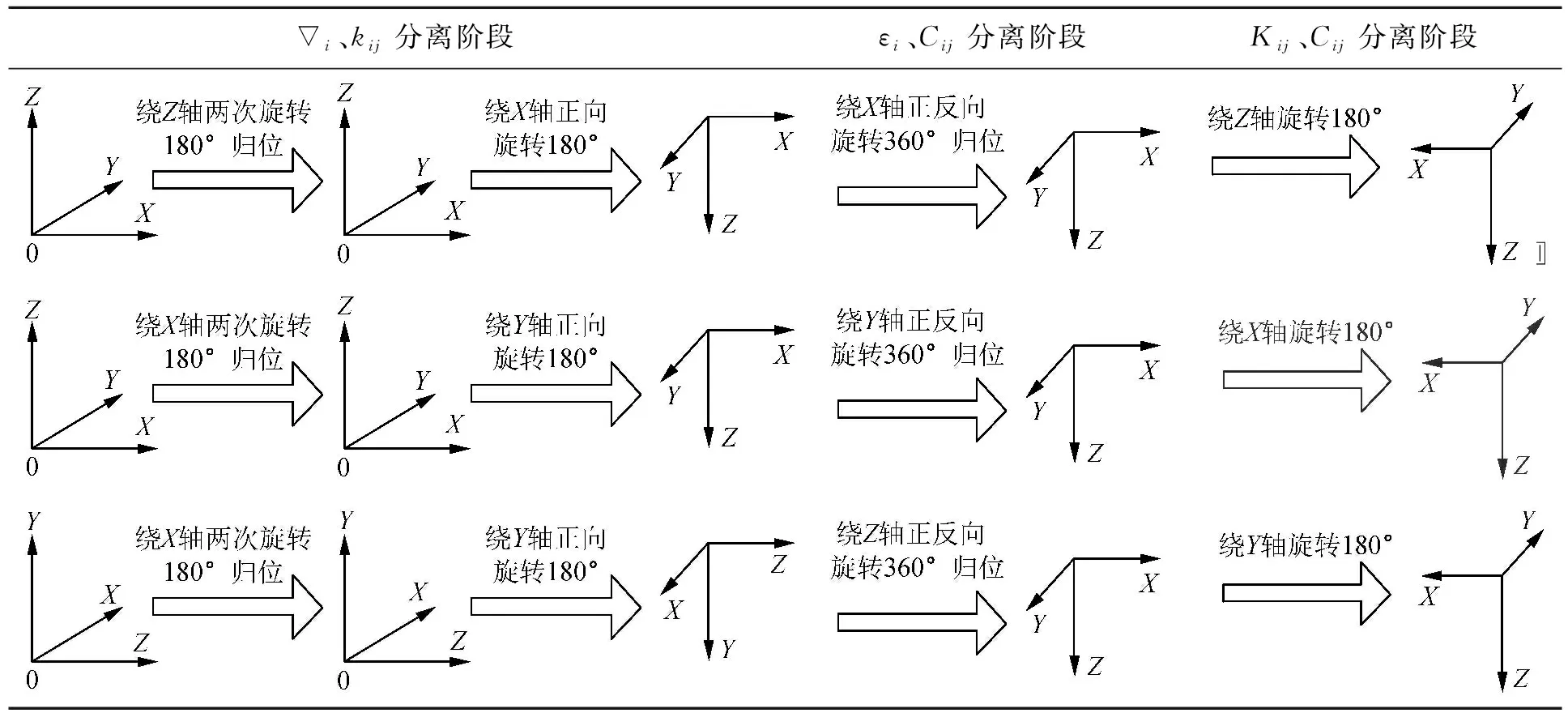
表2 标定路径

(5)在三轴转台运动的全过程中采集IMU输出数据，进行包括导航解算在内的离线处理[18]。

(6)通过卡尔曼滤波估计出陀螺仪误差和加速度计误差，然后将主捷联惯性测量装置的加速度计输出看作是实际的加速度，陀螺仪输出看作是实际的角速率，通过最小二乘法分离标度因数和安装误差参数[19]。

3 测试与实验

以IMU-500型惯性测量单元作为基准惯组，以MIN-900型惯性测量单元作为被测惯组，二者固连于UOO型惯性测试标定设备进行测试。分别以速度+姿态+位置匹配、速度+位置匹配、速度匹配作观测量，设置3组对照组，对比3种传感器布控方法对于标定结果和标定效率的影响。

3.1 测试条件

被测惯组和基准惯组都经过高精度三轴转台标校，其主要性能参数如表3所示。

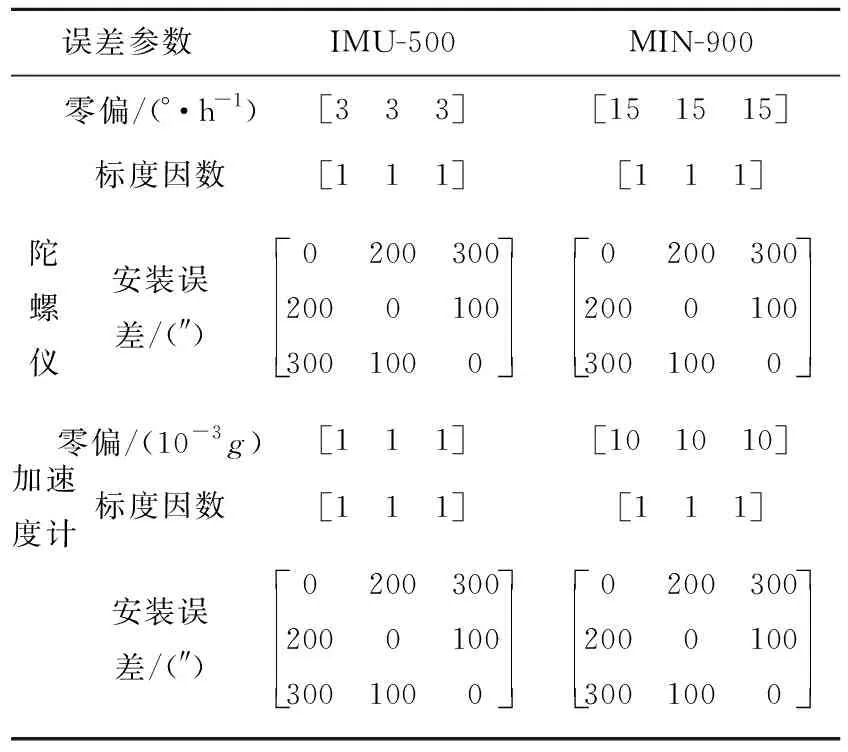
表3 惯组性能指标

实验采用UOO型惯性测量单元测试标定系统进行IMU的标定。测试设备的实物如图3所示。

该设备能提供速率、位置、摇摆等运动控制，并且能够实时采集被测惯性测量单元的原始数据信息，导航解算之后进行存储以便后端处理。测试标定系统为MEMS惯组的静态标定测试提供恒定转速，做为惯组测试信号源，通过上位机控制转台内框、中框、外框以固定步长旋转和固定时间。

相较于大多数高精度大型三轴转台，该测试设备具有小型化、易于外场机动的特点，但是需要配备隔振基座，角速率控制精度和角位置控制精度也远低于传统设备。

图3 惯性测量单元测试标定系统

根据表4，该设备属于低精度测试转台。测试标定系统的具体指标如表4所示。

表4 转台精度分类

表5 惯性测量单元测试标定系统性能指标

3.2 实验结果

测试中，以高精度转台标校后的参数，即表3中主子惯组的性能指标作为基准，共设置3组对照组,分别是速度+位置+姿态匹配、速度+姿态匹配以及速度匹配。在对卡尔曼滤波器设置不同观测量的情况下，观察IMU标定的精度以及滤波器收敛的速率,如表6和图4～5所示。

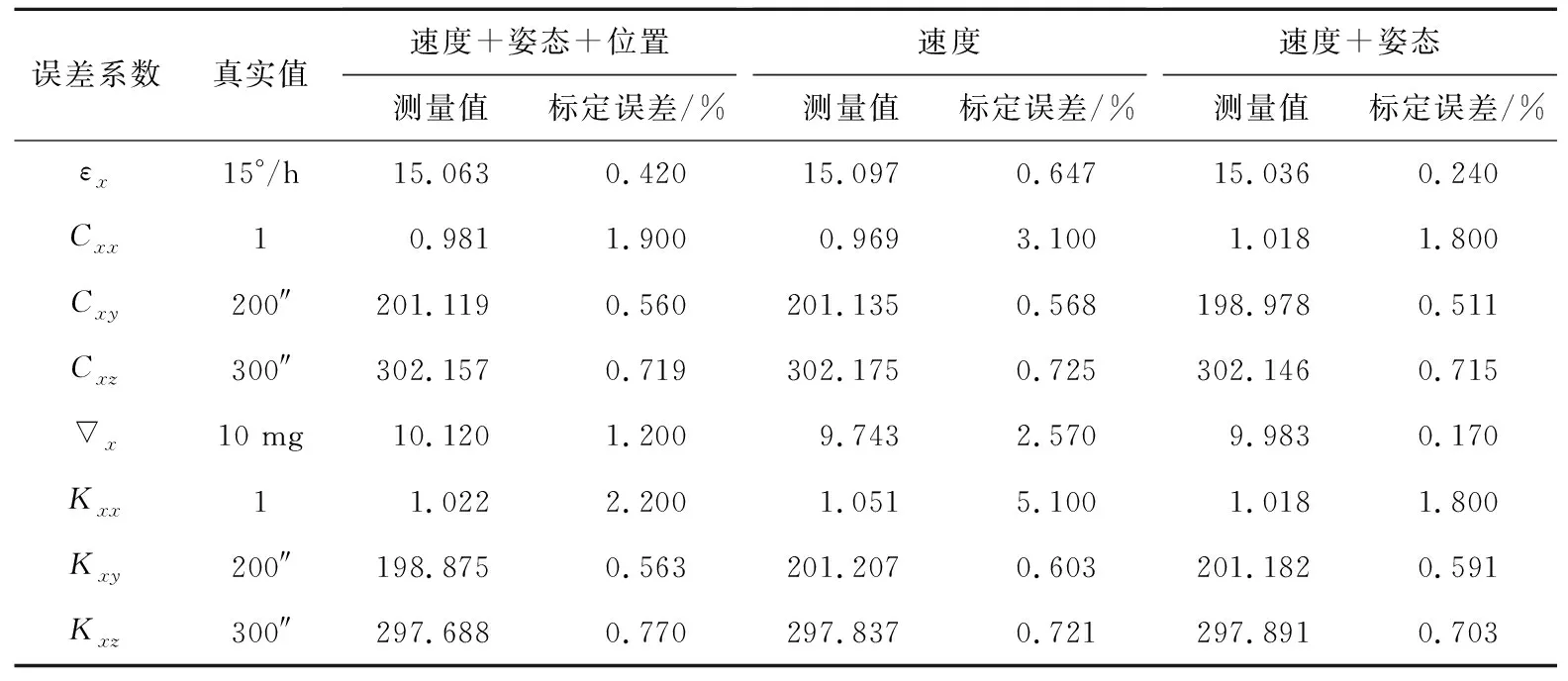
表6 陀螺仪X轴参数标定误差

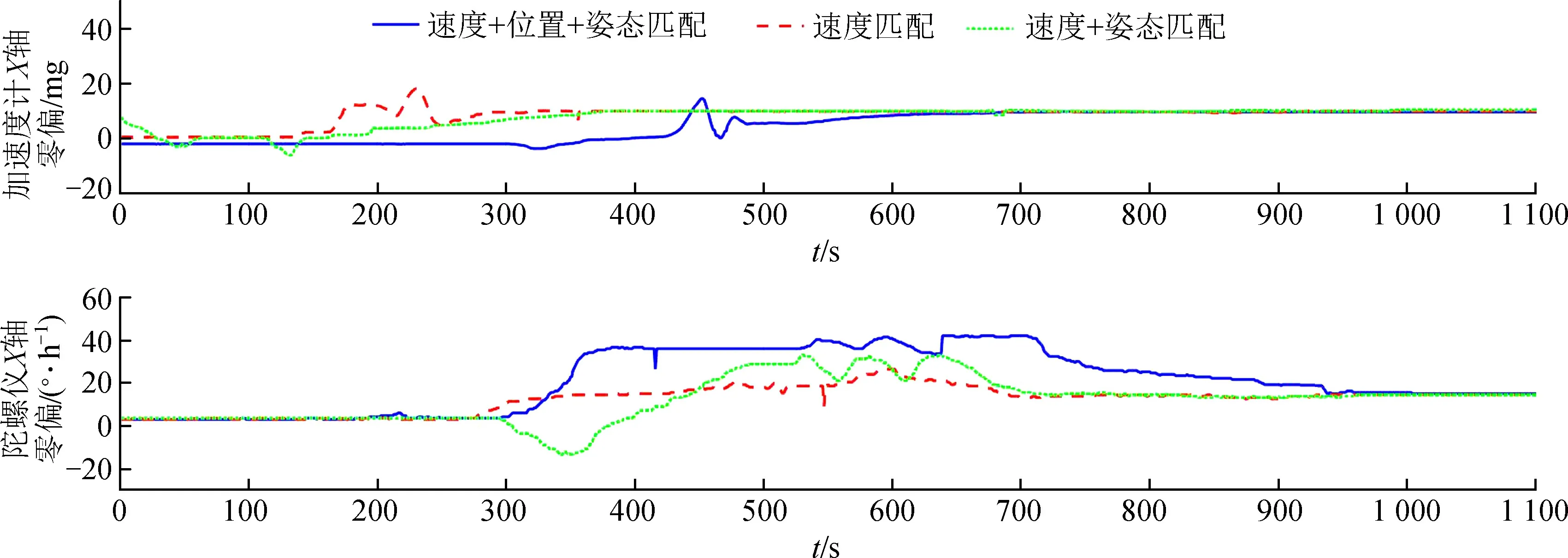
图4 不同观测量标定结果对照图

图5 惯性测量单元安装误差估计

通过对表6与图4～5分析可以得出：对于大多数误差参数，速度+姿态匹配方法标定的标定误差最小，速度+姿态+位置匹配方法次之。但是速度+姿态+位置匹配方法在卡尔曼滤波器中的收敛速度远慢于其他2种方法，基本上要推迟>250 s之后才能收敛至准确数值。因此，速度+姿态匹配的方法标定误差最小，收敛速度最快，运算复杂程度适中，在3种匹配方法中最优。

通过图6和图7对误差补偿前后惯组的一系列测试，证明本文提出的主子惯组匹配标定方法补偿效果更优，而且本方法能够在一定程度上补偿低精度转台各项误差造成的标定精度降低的问题。

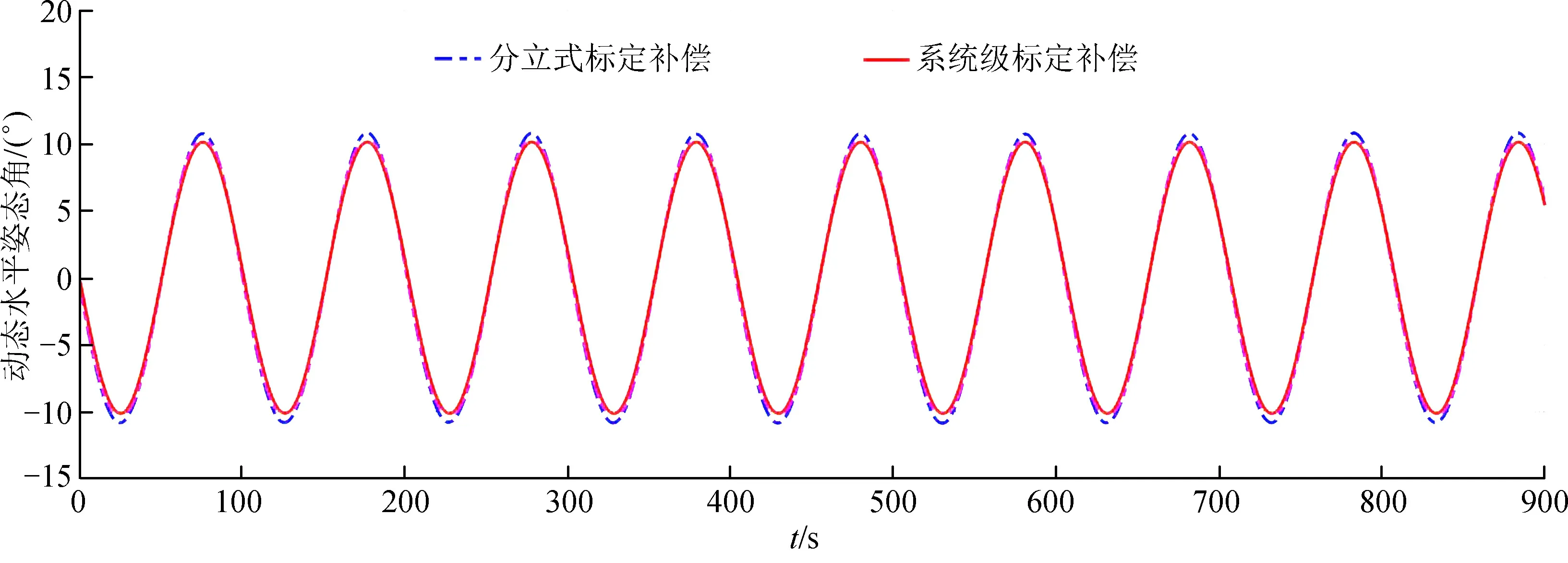
图7 动态姿态角补偿测试曲线

4 结 语

基于卡尔曼滤波的主子惯组匹配标定算法可以在低精度三轴转台上实现IMU的快速标定，标定精度在可接受范围内。将速度+姿态匹配作卡尔曼滤波器观测量时，系统标定精度最高，滤波器收敛最快，计算量适中，适合实际外场标定时的工程应用。