三维浮体的二阶波浪力计算研究
2021-01-21张君彦李文华林珊颖葛杨元
李 男 张君彦 李文华 林珊颖 葛杨元
(1. 大连海事大学 轮机工程学院 海底工程技术与装备国际联合研究中心 大连116026;2. 中国船级社质量认证公司 北京100006;3. 南通力威机械有限公司 如皋226500)
引 言
随着海洋资源开发的不断发展,海洋结构物的直接计算设计被广泛采和。海洋结构物受系泊系统的影响,存在低频慢漂和高频共振响应,非线性的差频与和频波浪力计算关系到平台的运动性能、系泊和采油设备的设计,是浮式海洋结构物设计的关键计算内容之一。[1]
基于频域二阶理论,二阶非线性波浪力包含一阶势产生的二阶力以及二阶势产生的二阶力两个部分[2]。一阶势产生的二阶力计算公式推导相对简单,但受计算机能力及速度势偏导数算法细节的影响,近场公式很难获得准确的精度,而远场公式只能给出纵荡、横荡和横摇的定常力,仍需进一步研究。刘滋源[3]、王磊等[4]开展了有限水深的定常力计算研究,段文洋[5]基于泰勒展开法获得了较高精度的切向导数,并开展了二阶定常力的计算研究,获得了较为精确的结果。
对于二阶速度势求解,国内外学者进行了广泛持久的深入研究,最早获得了回转体的解析解,如缪国平[6]在二阶绕射势产生机理的基础上给出了二阶绕射势的解析解。随后针对回转体进一步尝试了结合解析解的数值匹配解法,此外针对二阶辐射势的定解条件也一致在探讨中。Kim和Yue[7-8]首次将非齐次项放到绕射势求解中,使辐射势的求解和一阶势相同,同时该方法通过对速度势的远场展开扩展到任意三维浮体,并基于此开发了WAMIT[9]软件,国内学者也采和类似方法开展了相应的研究[10]。由于近场方法求解速度势高阶导数精度受限,一直致力于非线性水动力计算研究的Chen开发了HYDROSTAR软件[11],并创造性地提出了中场方法[12],大大提高了二阶力和二阶势的求解精度,使HYDROSTAR软件声名鹊起。此外,为提高高阶偏导数的计算精度,高阶B样条面元法[13]被引入到二阶水动力计算中,WAMIT软件也开发了基于B样条面元法的高级版本。AQWA[14]软件在结合工程实际,在考虑一阶势二阶力的基础上,引入二阶绕射势的近似考虑方法,避免了求解二阶绕射势,但在差频力计算中取得很好的效果,值得借鉴。
由于二阶波浪力计算的复杂性,要获得较准确的结果需要注意的细节较多,国内目前仍少有能够获得较高精度二阶力结果的计算软件,浮式海洋结构物相关设计和研究主要采和国外软件,限制了相关技术细节的掌握及深入研究的进一步开展。在当前国外屡屡对我国实施卡脖子策略,开展二阶波浪力计算研究,掌握相关的技术细节,对为未来持续深入开展水动力计算研究,培养脚踏实地的水动力计算研究人员,以及开发相关软件十分必要。
本文基于前人的研究成果,开展二阶波浪力计算的相关研究,对其中一些计算细节进行了摸索和总结,获得较满意的结果。
1 一阶势二阶力计算公式
1.1 一阶势二阶力计算公式简介
基于频域二阶理论的近场方法,对各物理摄动展开保留到二阶,若二阶运动产生的回复力不放在二阶力传递函数计算中考虑,则三维无航速浮体一阶势产生二阶力(力矩) 的计算公式[2,15]如下:

式中: 为六自由度运动位移; 为三个平动位移矢量,m; 为3个转动位移矢量,rad;n为六自由度法向量;r为湿表面上点到重心的矢径,m;ρ为水密度,kg/m3;g为重力加速度,取为 9.8 N/kg;(x,y,z)为湿表面上一点坐标;F(1)为一阶力(力矩), N(N·m);Φ为一阶速度势。式中4项分别为转化为水线积分的湿表面变化项、伯努利平方项、一阶力(力矩)转动项和平均湿表面转动项。
1.2 和频及差频计算推导
相关著作[2,15]虽然给出了类似于式(1)的一阶势二阶力计算公式,但没有给出2个一阶量合成二阶和频和差频项的公式,尤其是人为变化出的对称属性在二阶力传递函数矩阵中的应和,若不考虑这一属性,将使矩阵元素的结果与商和软件不一致而令人产生困惑。
基于二阶频域理论,为简化推导,假设波幅为a1和a2(包含相位的复数)的2个线性子波为Aj和有2个响应变量的C和D,其在频率ωj和ωl的响应分别为
则对于这2个子波,C和D相乘的二阶量可以表示为:

上式等号右端第1部分为和频分量,按子波分量改写成关于主对角线对称的矩阵形式,可以表示为:

式(2)中间的矩阵为和频力传递函数矩阵。等号右端第2部分为差频分量,-表示共轭运算。
由于互为共轭的2个复数的取实部结果一致,差频力可以表示为关于主对角线共轭的形式为:
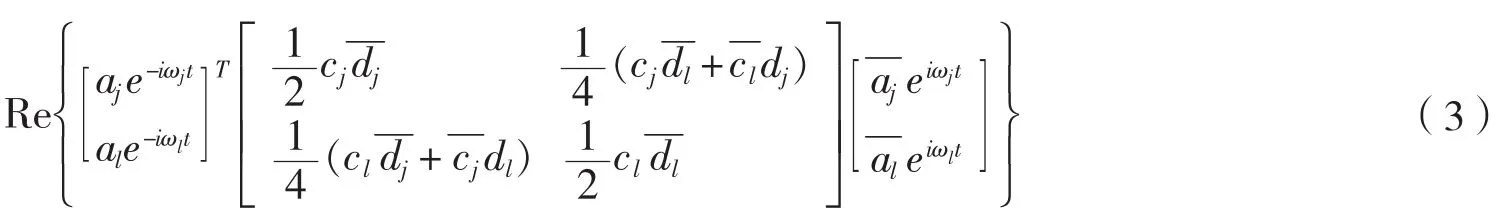
式(3)中间的矩阵为差频力传递函数矩阵。
需要特别说明的是,这里关于主要对角线元素的对称或共轭属性是在各子波分量合成结果不变的情况下人为变换得到的,考虑这一属性将导致二阶力传递函数矩阵的单个元素与不考虑不同,但两者最终的合成结果一致,与相关国外软件(如AQWA和HYDROSTAR)对比时需要注意这一点。
通过式(2)和式(3),可以将式(1)的二阶力(力矩)表示为各分量的传递函数的计算形式,且由于矩阵的对称或共轭属性,只需求解一半即可。多个频率的传递矩阵可参考以上方式按多个子波分量获得。
1.3 二阶入射和绕射差频力近似计算
对于2个线性子波,满足二阶自由面条件的二阶差频入射波势的表达式为:

又一阶入射波势的表达式为:

此处:ω为频率,为波数,且为水深,m;(x,y,z)为湿表面上点坐标,m;j和l为分量角标;I为入射波。
参考AQWA软件[14],假定二阶差频绕射力和一阶力有同样的关系,二阶差频绕射力传递函数也可以通过式(5),由相同波数的一阶绕射波力获得,这样就可以考虑近似考虑二阶差频力传递函数中二阶势的影响。
1.4 计算程序信息
基于以上理论推导,采和FORTRAN语言进一步开发了二阶波浪力计算的计算程序。考虑到二阶力计算精度要求高、计算量较大,推荐使和的内存不低于8 G、硬盘不小于10 G。此外,程序包含了对称性在水动力计算中的应和,使计算效率大大提高。目前,一万水动力网格单线程计算一个频率的时间(与网格数量的平方成正比)约为5 min,与国外AQWA、 HYDROSTAR等软件的计算效率接近。
2 算例FPSO的定常力及成分分析
为验证本文相关公式推导和计算的正确性,本文选取一艘典型的FPSO为例,将相关计算结果与AQWA软件结果进行比较。
2.1 算例基本参数
算例FPSO基本型线见图1,相关参数见表1。
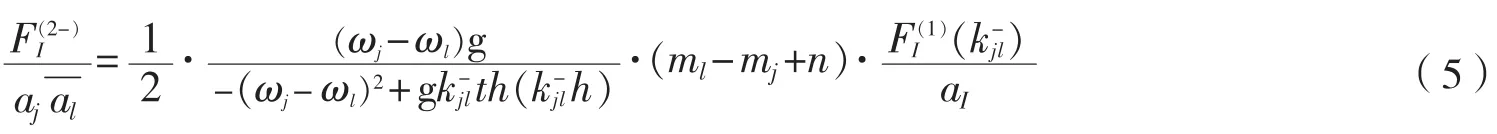
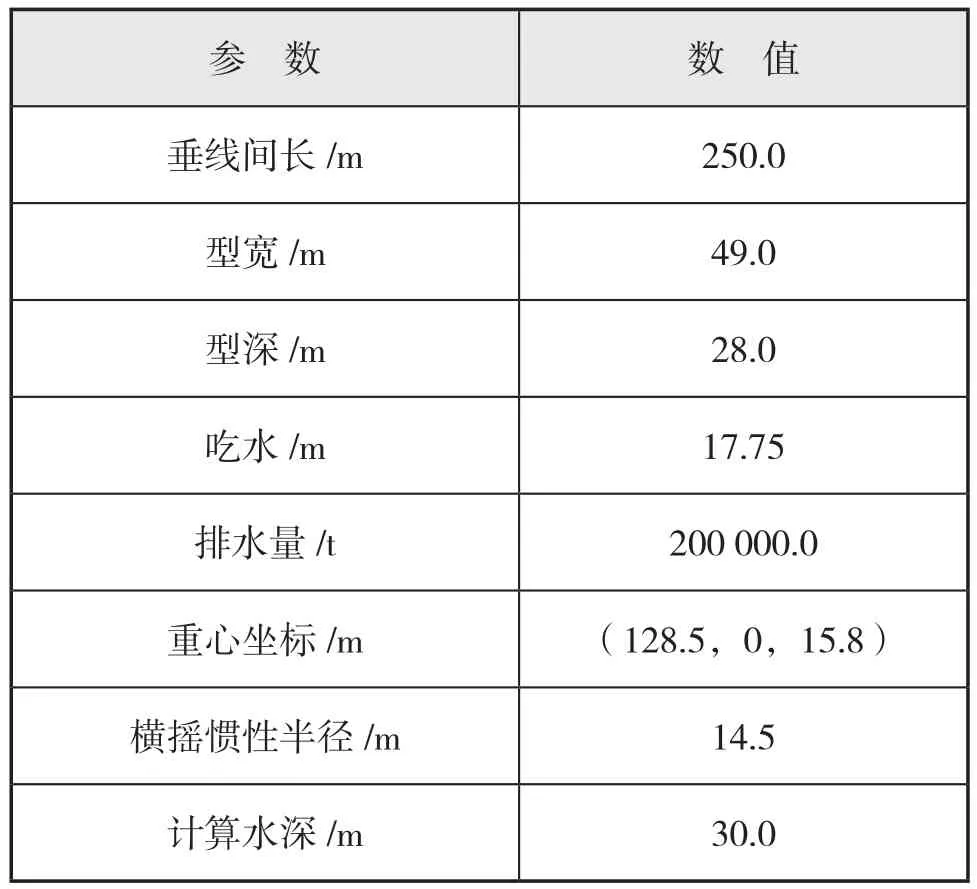
表1 算例FPSO相关参数表
半船船壳湿表面网格4 100个,内域自由面网格229个,水动力网格见图2。

图2 湿表面网格和内域自由面网格图
2.2 定常力计算结果
2.2.1 自由面刚性网格对计算结果的影响
进行水动力计算时,通常会遇到不规则频率问题,通常的做法是增加湿表面网格或者通过扩展边界积分法[16]在内域自由面增加刚性网格来消除不规则频率。经过实践计算发现,在计算二阶力时,由于需要考虑速度势偏导数的影响,若不采和扩展边界积分法,即使一阶响应没有不规则频率的影响,二阶结果仍会出现许多振荡,图3给出不考虑内域自由面网格的横荡一阶激励力和二阶定常力结果。
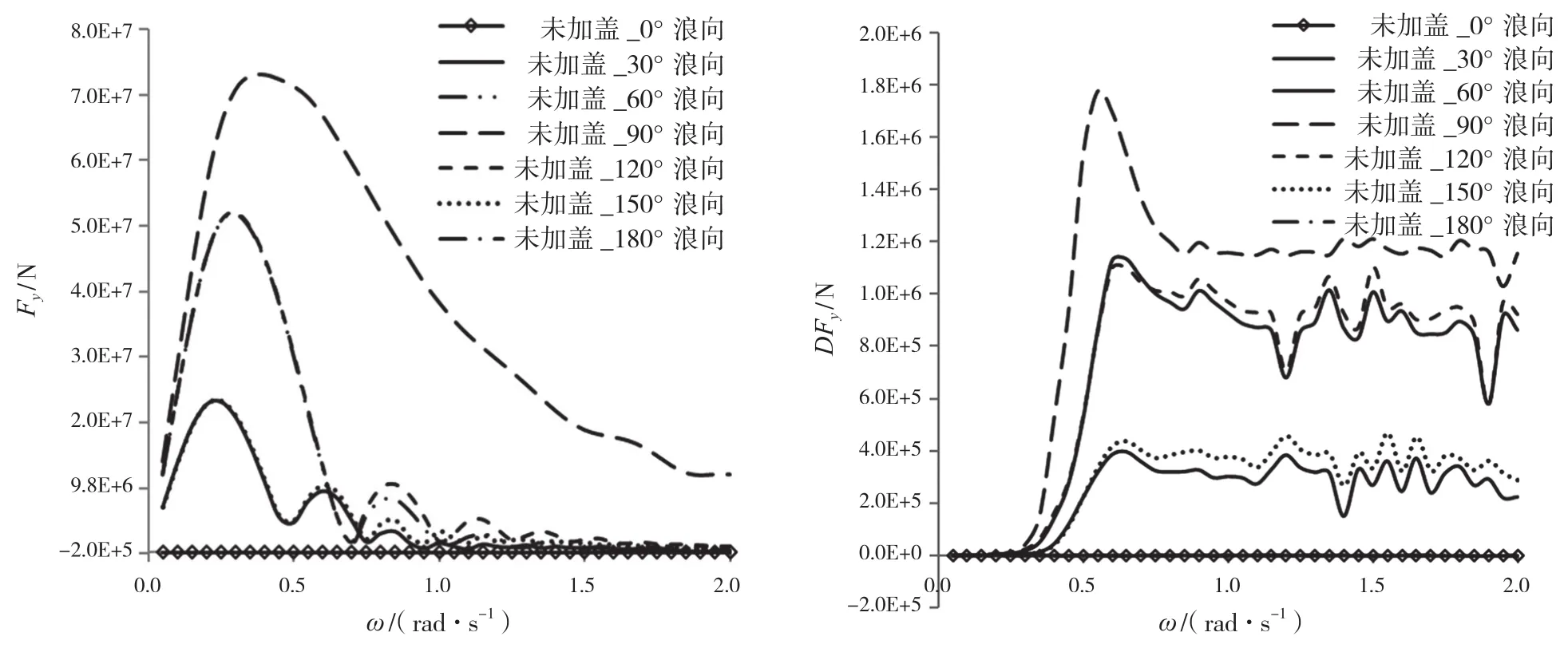
图3 未考虑内域自由面网格时横荡一阶激励力和二阶定常力结果
从图3可以看出,虽然一阶激励力结果很光顺,但即使采和半船4 100个网格,定常力结果与图4相比振荡仍较多。因此,在计算二阶力时,尤其是水线面面积较大的浮体,需要采和扩展边界积分法。
2.2.2 定常力计算结果与AQWA软件的对比
算例FPSO的纵荡、横荡、横摇及艏摇定常力结果对比见图4和下页图5。计算结果表明,本文与AQWA软件的定常力结果吻合良好。

图4 本文与AQWA软件的纵荡及横荡定常力结果对比图
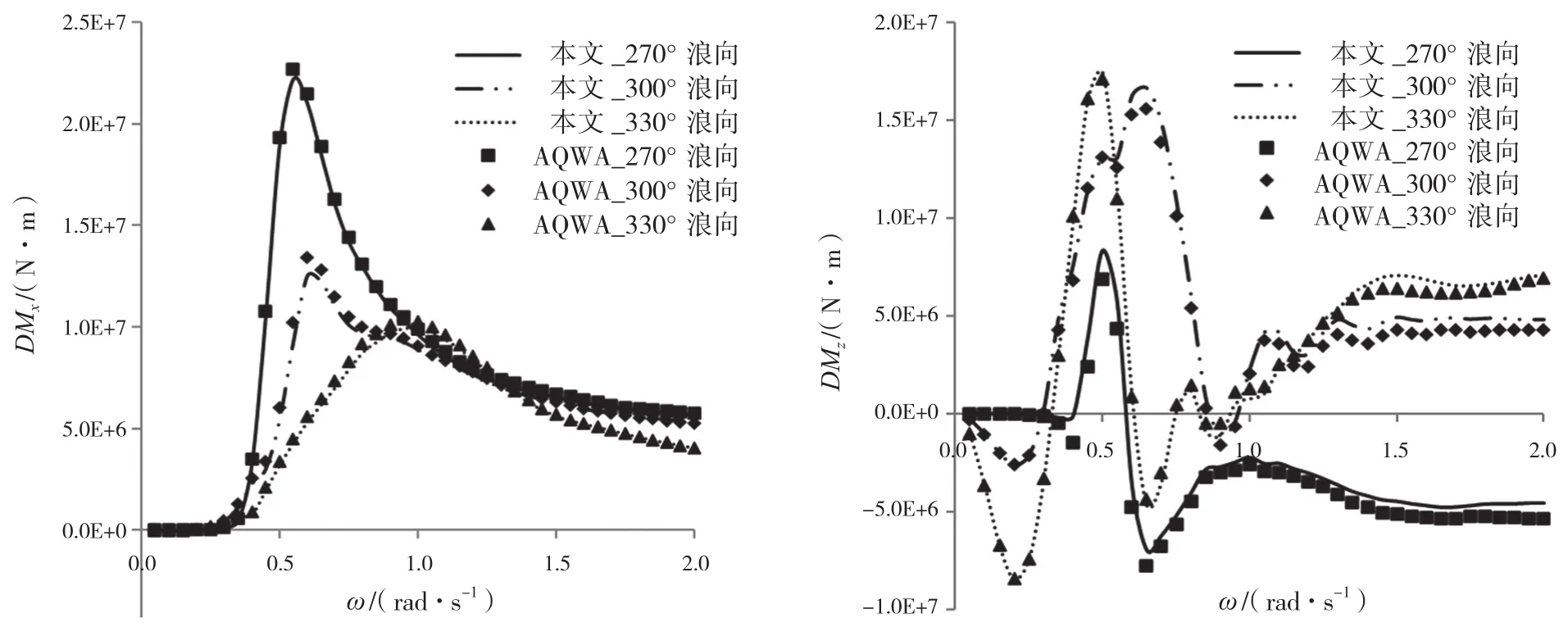
图5 本文与AQWA软件横摇和艏摇定常力结果对比图
2.2.3 定常力各成分分析
为深入了解定常力,进一步给出定常力响应最大时对应浪向四部分组成的结果,见图6至下页图8。
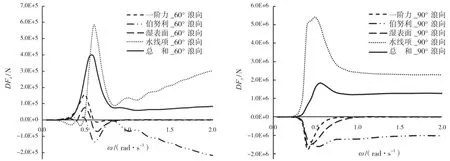
图6 纵荡定常力和横荡定常力各分量结果
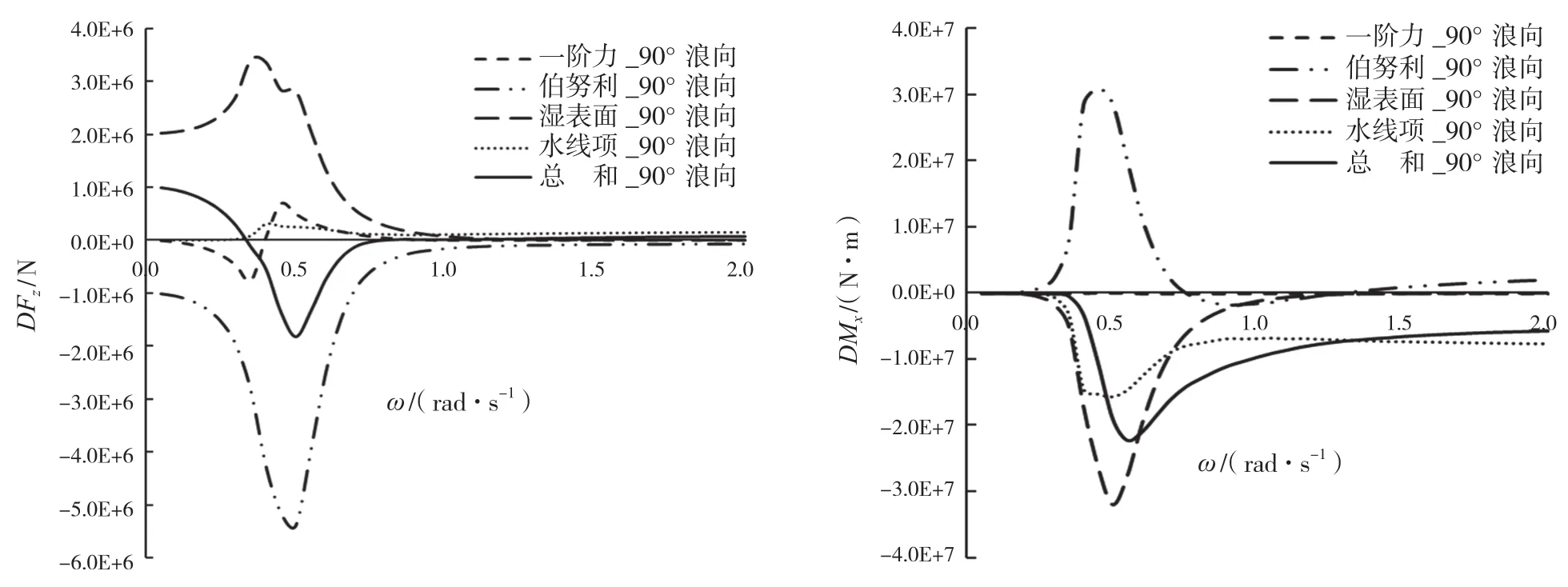
图7 垂荡定常力和横摇定常力各分量结果

图8 纵摇定常力和艏摇定常力各分量结果
由图6至图8的结果可以看出,各组成部分的符号不同,有的分量绝对值比总和结果还大,任何一项计算不准确都会导致最终结果产生差异,计算要求精度较高。另外,高频分量主要由伯努利项和水线积分项确定。
2.3 二阶力传递函数计算结果
为验证本文相关推导和程序的合理性,进一步开展了算例FPSO的二阶力传递函数计算验证。
2.3.1 二阶和频力传递函数计算结果对比
算例FPSO的二阶和频力传递函数对比部分结果见图9以及下页的图10和图11。其中:角标S表示和频,D表示差频,C表示实部,S表示虚部。可以看出,本文与AQWA的结果吻合良好。

图9 0°浪向的垂荡二阶和频力平方传递函数对比
2.3.2 二阶差频力传递函数计算结果对比
算例FPSO的Δω= 0.05 rad/s时,二阶差频力传递函数部分结果见下页图12-图14,结果吻合良好。
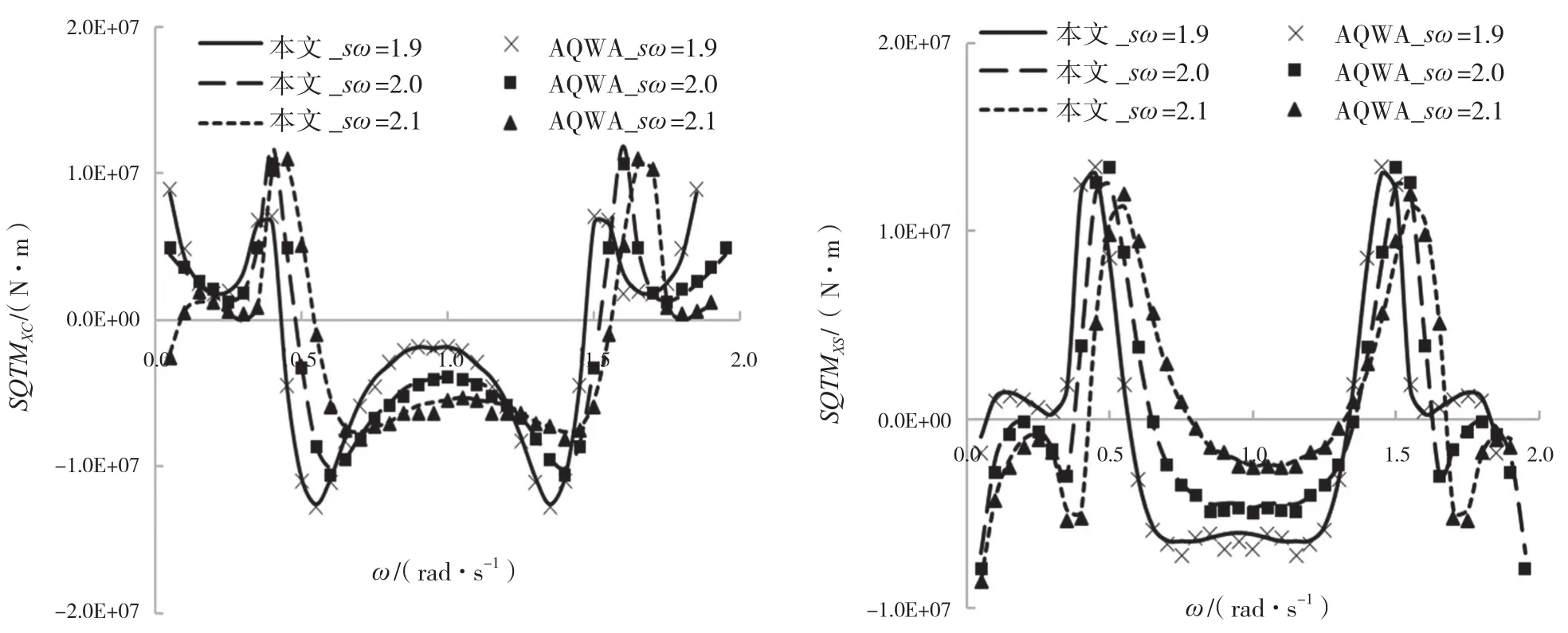
图10 90°浪向的横摇二阶和频力平方传递函数对比

图11 60°浪向的纵摇二阶和频力平方传递函数对比
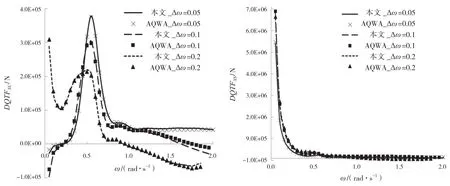
图12 60°浪向的纵荡二阶差频力平方传递函数对比

图13 90°浪向的横荡二阶差频力平方传递函数对比
2.3.3 二阶差频势对二阶差频力传递函数影响
本文进一步分析水深对二阶差频力平方传递函数影响,以及二阶差频入射势和绕射势对二阶差频力平方传递函数的贡献随水深的变化,水深为30 m、45 m、60 m和300 m,频率差为0.05 rad/s的结果见图15至下页图17。

图16 90°浪向不同水深二阶横荡差频力平方传递函数结果
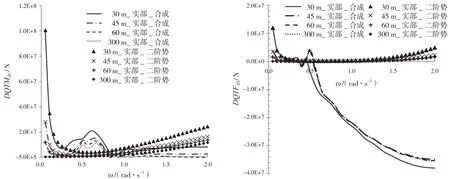
图17 60°浪向不同水深二阶艏摇差频力平方传递函数结果
从图中结果可以发现:
(1)二阶差频力平方传递函数的幅值随着水深的增大逐渐减小,且其随水深增大变化较快,水深达到吃水的4倍左右时水深增大引起的变化可以忽略;
(2)二阶差频入射势和绕射势对二阶纵荡和横荡差频力平方传递函数的虚部、艏摇差频力平方传递函数的实部影响较大,该影响随水深的增大逐渐减少到可以忽略。此外,二阶差频入射势和绕射势对二阶垂荡和纵摇差频力传递函数的实部和虚部、二阶横摇差频力传递函数的虚部影响较大,本文限于篇幅没有列出相关结果图。
3 结 论
本文基于一阶势的二阶力计算方法,给出定常力、二阶力传递函数的相关计算公式推导,并引入二阶入射和绕射差频力的近似考虑方法,通过编制相关程序进行验证,达到了AQWA软件的同等精度,为后续开发国产二阶水动力计算软件奠定了基础。此外,通过以上研究,得到以下经验结论供其他研究者参考:
(1)以适量的网格并采和扩展边界积分法,近场方法也可获得精度较高的二阶力传递函数。
(2)二阶力各组成分项符号不同,有的分量绝对值比总和结果还大,形成合成量为大值差的形式,要求计算精度较高,任何一项计算不准确都会导致最终结果的差异。
(3)二阶差频力平方传递函数的幅值随着水深的增大逐渐减小,且其随水深增大变化较快;当水深达到吃水的4倍左右,水深增大引起的变化可以忽略不计。
(4)有限水深时,二阶差频入射势和绕射势产生的差频力对二阶差频力传递函数影响较大;该影响随水深的增大而逐渐减少到可以忽略不计。
(5)与不同软件对比时,要明确一阶势二阶力计算公式中是否考虑二阶运动引起的静回复力非线性,二阶力传递函数矩阵计算中是否考虑了关于主对角元素的对称算法。
