深度学习促生长高阶思维亮课堂

【关键词】深度学习;高阶思维;情境教学;支架

作者简介：王艳兰（1991.8—）女，江苏常州市新北区奔牛实验小学，中小学二级教师。

北京师范大学郭华教授指出，深度学习是在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。深度学习的关键是高阶思维，就是指发生在较高认知水平层次上的心智活动或认知能力。在情境教学中，教师根据学习的内容以及学生的兴趣，设置有趣生动的情境，促使他们产生自主探究的欲望，从而进一步达到教与学的有效统一。在教学中，学生遇到困难时，教师适时提供语言、工具等支架的支持，让学生能够有启发性地继续展开学习，从而获得最佳的教学效果。

一、创设情境，激发学生求知欲

教育家夸美纽斯在《大教学论》中写道：“一切知识都是从感官开始的”，这种论述反映了直观在教学过程中的重要性。情境教学就是立足于感官，在数学教学过程中，教师有目的地引入或创设以形象为主体的生动场景，从而促使学生更容易理解教材的教学方法。情境教学法的运用，能给学生展示鲜明具体的形象，使学生从形象感知到达抽象理解，关键还能激起学生的兴趣。其实，情境就是架在学生与数学中的桥梁，它打破了学生原有的认知方式，能让学生的数学学习从“被动接受”转变为“主动参与”。在教学活动中，学生是课堂教学活动的主体，教师是引导者。教学目标的达成情况，是要以学生的认知成效为依据的。所以，教师的“教”必须落实到学生的“学”上，要让学生掌握学习的主动权，使学生站在课堂的正中央。教师要创设和谐轻松的课堂学习氛围，引导学生自学教材，使学生积极参与小组讨论，进而掌握解题策略，让学生的生命活力在课堂上得到充分释放。

现在学生对主要的学习载体—教材缺乏兴趣，对辅助性学习载体—视频、游戏等情境情有独钟。学生的学习需要兴趣，因此，在数学课堂中，教师要利用好情境教学，让学生在求知欲中产生学习动力。在《圆的周长》一课中，通过创设3个车轮滚动一周的情境，让学生比较哪个车轮滚动的路程长，然后动画演示车轮滚动一周，从而揭示课题“圆的周长”。车轮滚动是学生在真实生活中会接触到的场景，以已有经验为出发点，有助于学生在熟悉的场景中抽离数学上“圆的周长”的概念，产生解决问题的迫切欲望。正确应用信息化的手段，把学生带到“圆的周长”这一课中来。另外，不同年龄阶段的学生，对情境的兴趣指向性存在明顯的差异。所以在创设情境的过程中，要充分考虑学生原有的知识基础、年龄和心理发展的特点，创设他们感兴趣的、能激发他们求知欲的情境。车轮滚动的场景符合五年级学生的认知发展与思维水平，在教师富有感染力的语言描绘以及动画演示下，更能提高学生的感知效率。

阿尔弗雷德·比奈的实验证明，在儿童身上天然存在接受暗示的能力，这种“可暗示性”即“可教育性”。虽然数学是一门理性的学科，但是利用好情境，就能让数学思维发光发亮。蕴含着数学知识的情境，能够调动学生原有的认知结构，经过思维的内部整合作用，学生就会有所领悟，这就是情境的启迪作用。《圆的周长》一课中，车轮滚动一周所行驶的路程就是车轮的周长，也就是即将学习的圆周长的概念。然后对3个车轮的周长进行比较，猜想影响圆的周长大小的因素就是半径（或直径）。在这些情境中，学生能够一步步接收教师的暗示并深刻领悟，弥补自身的感性认识之不足，从而实现在认知上的发展，让思维向纵深发展。另外，教师在设计情境时，要指向数学知识的理解、数学思维的发展、数学知识的迁移，以学为中心，认真思考这些情境所要体现的数学思想。所以在处理教材时，教师本身要做到“知其然而知其所以然”，设计出科学却不失“热闹性”的情境，这样才能激发出学生探索数学的兴趣。

二、支架助学，引导学生自主探究

支架是教师在教学过程中，为学生建构对知识的理解、问题的解决提供的帮助。支架助学可以是课堂中为学生的自主学习提供适当的、小步调的线索或提示，也可以是关键性的追问与启发，从而使学生逐渐发现和解决学习中的问题，掌握所要学习的知识。著名心理学家维果斯基提出的“最近发展区”理论，为支架助学提供了有力的心理学依据。他认为学生发展有两种水平，一种是学生的现有水平，另一种是学生可能发展到的水平。在儿童智力活动中，教师提供的支架可以帮助学生实现发展，从而达到下一发展阶段的水平。小学数学新课程标准指出，教师是学习的组织者、引导者与合作者，学会为学生提供合适的支架，有利于推动学生主体地位的实现。教师要应用有效的学习工具（包括学习单、思维导图等），准确引导学生自主学习，满足学生的个性化需要。

《圆的周长》一课中，支架助学主要从以下两个方面体现：

1.在猜想圆周长与直径的关系时，教师提供了一张图（见右图）：在正方形里画一个最大的圆，接着在圆里画一个最大的正六边形，六个顶点都在圆上。通过正方形周长（4倍的直径）与圆周长的比较，得出圆周长比直径的4倍要小;通过正六边形周长（3倍的直径）与圆周长的比较，得出圆周长比直径的3倍要大。综合两次比较，学生能直观得出，正方形的周长大约是圆直径的3倍多一些。通过图片，学生猜想到圆周长与直径的倍数关系，克服了教学中的难点，并能更清晰、更深入地思考。这一设计符合学生的逻辑思维，让学生的深度学习更加具有方向性。

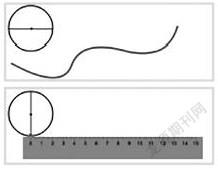
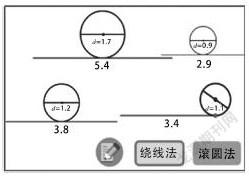
2.测量4个圆片（直径已知）的周长时，对于学习有困难的学生，教师在iPad里放入资源包，通过资源包里的动画，直观演示测量的两种方法，即滚圆法和绕线法。学生之间是有个体差异的，针对能力较弱的学生，教师需要利用相关辅助工具，尽力做到关心每一个学生的发展。另一方面，小学生受到自身年龄的影响，他们的思维以具体形象为主，用Flash动画演示测量方法，既直观又高效，让学生一下子抓住本质特征。

在开展小组活动之前，教师需要明确相应的活动要求，在相关提示下，避免学生理解偏差。比如两次实验操作前，教师会请学生朗读活动要求，并明确组长的职责，保证好小组活动的高效开展，做到全员参与，独立思考与交往互动协调发展。

探索圆周长与直径的关系时，教师先起到启发引导的作用，让学生从支架中获得猜想，然后再去分析。这样有助于学生突破难点，有所领悟与启发，为后续的学习做铺垫。探索过程中教师适时关注学习有困难的学生，帮助能力稍弱的学生也能准确测量，减少实验误差。提供支架的同时，也注重培养学生独立思考的能力，而不是一味地、盲目地帮扶。起初的引导、帮助可以多一些，然后逐渐放手让学生自主探索，自然而然地促进学生深度学习。教师还应当鼓励学生在小组合作交流时，做到大胆发言、认真聆听并及时评价的过程性习惯，师生共同努力营造自然清新、灵动和谐的氛围，让学生在互动中“求真知、明道理”。久而久之，每位学生都参与课堂，在教师的引导下积极互动，他们就自然而然会思考、能思考，那么深度学习也不需要教师再劳心劳力了。

三、实验操作，丰富学生深度体验

著名的教育思想家卢梭认为：“通过儿童自身活动，获取的知识比从教科书、从他人学来的知识清楚得多、深刻得多，而且能使他们的身体和头脑得到锻炼。”因此，在我们小学数学教学中，教师应当放手让学生去体验、去活动，从自身操作的实验活动中获得数学知识，会直接得多。小学数学新课程标准指出，除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式，学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。因此，实验操作也是课堂迸发思维活力的有效方式，有利于促进学生分析、理解，从而得出相关结论。在实验操作之前，教师需要带着学生一起明确实验要求，有条理地推进实验过程，避免操作失误。

在《圆的周长》一课中，进行了两次实验，分别是4个圓片周长的测量与电脑验证。初次的实物测量实验，学生通过小组合作，利用滚圆法和绕线法，记录下4个圆片的周长，然后与直径进行比较，算出周长除以直径的商。教师汇总全班数据，小组汇报交流得出周长除以直径的商都是三点几。教师适时提问，“对于直径相同的圆，为什么各小组测量的周长数据互相之间有差异”，从而明确实际测量中会产生误差，需要更精密地测量更多的圆、不同的圆。

那么自然引出第二次测量，就是通过电脑软件，学生可以画任意的圆，滚动一周后，由电脑量出它的周长进行计算并记录。这样又快又准确地测量与计算，进一步丰富学生的操作体验。从全班的测量数据中，学生快速得出周长除以直径的商都是一个固定的无限不循环小数，就是圆周率。开展实验活动，让学生调用已有的知识经验，主动形成对问题情境的思维成果，引导学生在做一做、验一验中对猜想进行验证，从而得出正确的结论。课堂上能让学生观察的尽量让学生观察，能让学生动手的尽量让学生动手，让学生的动手动脑能力得到充分的发展。在课堂上充分合理地运用实验教学，能够有效引导学生自主建构，发现相关规律、解决疑惑，并体验到数学知识的奥秘所在，激发学生学习数学的热情，最终达成教学目标。

四、精讲精练，促进学生思维生长

从心理学角度看，学生在课堂上听课注意力集中时间是有限的。根据有关研究表明，小学生课堂上注意力高度集中一般在10～20分钟，因此，教师在教学过程中拖沓、重复知识点，反而会让学生出现注意力稳定性的衰退，就是“开小差”。因此，教师需要改变过去那种填鸭式的灌输教学方式，在全面把握知识的情况下，注意详略得当、突出重点、突破难点，充分调动学生的积极性，这就是精讲。另外，心理研究还发现了适当练习对技能学习有促进作用，但过量练习、重复练习会适得其反。教师在课前应设计好相关练习，根据不同学生的认知水平、思维水平，拟定不同层次的练习，专项练习、巩固练习、拓展练习。当然，练习后教师应当给予有效评价与小结，或者也可以开展同学互评。教学活动中教师的评价主要起着反馈、激励、调控、导向的作用，那么怎么做到点评到位，就要教师要根据当堂课的实际情况，有选择性地针对不同点进行评价。这样，才能使学生对教材的理解从片面走向深刻、从浅表走向内里，教学的重难点得到解决，最终实现教师、教材、学生三位一体的融合。

《圆的周长》一课中，学生交流得出圆周长公式后，随即在iPad上进行4道选择题的练习。学生独立完成后提交，教师端就能生成4道练习题的正确率以及完成情况等，教师可以有侧重、有针对地进行讲评。然后也能当堂发现掌握不熟练的学生，便于课后辅导。这让学生在解决问题的过程，学会灵活调用已有经验来判断和解答问题。以“练”提高学生对知识的理解，从而达到巩固知识的效果。课堂的最后，拓展研究圆周率的数学历史，让学生了解古代人的伟大，并学习他们不断钻研的精神，使学生对教材的理解从肤浅走向深刻，促进学生思维生长与情感的升华。把知识的发生发展历史以及关键人物的研究成果融合到教学中，在教学的同时，给学生渗透数学文化，推进学生后续学习，激励学生学好数学，将来在数学领域做出贡献。

总之，深度学习离不开深度教学，深度教学的关键是教师，教师需要做好提前准备，真正立足儿童，迎合儿童探究的天性。尊重儿童的身心发展规律，设置情境教学;尊重教育规律，提供支架助学;顺应时代发展，利用好各种教育资源，实施探究学习。教师除了整合教材中的数学知识，还必须采取恰当的教学方式，营造自然和谐的课堂氛围，调动和培养学生自主探究的能力，让学生在理解的基础上拾级而上，走向深度学习，促进思维生长。

【参考文献】

钟法旺.基于高阶思维能力培养的小学数学教学—以“长方体的认识（一）”教学为例[J].新教育时代电子杂志，2020（01）.

张素坤.让深度学习在数学课堂中真正发生[J].教育实践与研究（A），2019（01）：29-31.DOI：10.14160/j.cnki.13-1259/g4-a.2019.01.011.

王桂香.小学数学课堂教学中深度学习的策略[J].小学科学（教师版），2017（01）.

陈柏良.构建深度学习的数学课堂[J].中学数学教学参考，2017（31）：14-17.