湍动流化床颗粒流动特性的数值模拟

王 坤，朱丽云，李安俊，王振波，王国涛

(中国石油大学(华东)新能源学院，山东 青岛 266580)

当前我国的重油催化裂化工艺(RFCC)经过不断改革创新，逐渐趋于科学化、高效化，已经成为石油加工的核心技术和重质油轻质化的主要手段。随着原油日益重质化、劣质化，对再生器等设备的考验越来越大。催化裂化反应使焦炭沉积在催化剂表面上，导致催化剂活性急剧下降【1】，而再生器则通过烧去结焦催化剂上的焦炭来恢复催化剂的活性。为了提高目标产品收率、降低焦炭产率，工艺上通过提高系统催化剂循环量、改变再生器内气固流化形式来提高催化剂再生效率，促进裂化反应，保证催化剂活性。系统催化剂循环量增加和再生器内流化形式的变化均需要更高的流化气速，随着再生器内操作气速的提高，床层内气体夹带能力大大提高，大量的催化剂被带入稀相空间，降低了再生效率；同时气固分离设备入口浓度增大，分离负荷增加，设备效率降低，也降低了催化剂的回收率。针对上述问题，在深入研究湍动流化床内颗粒流动特性的基础上，对流化床及旋风分离器的结进行优化、改善催化裂化条件是十分必要的。

湍动流化床因其固含率高、气固接触良好、热质传递高效等独有的特点在目前FCC再生器中的应用已十分广泛【2-3】，而由于湍动流化床内气固运动复杂、各种测量技术的局限及实验条件存在限制，目前针对湍动流化床中颗粒运动规律的研究仍较少。随着数值算法的发展以及各种商用软件的兴起，计算颗粒流体动力学(CPFD)【4】已经逐渐成为研究气固两相流的重要手段。计算颗粒流体动力学(CPFD)数值模拟方法采用欧拉-拉格朗日方法来求解气固的流动特性【5】，该方法基于MP-PIC(multiphase particle-in-cell)【6】，可以解决流化床等大型设备中颗粒与流体的耦合问题。欧拉-拉格朗日方法是将流体视作连续相，在欧拉坐标系下考察流体相的运动；颗粒视作离散相，在拉格朗日坐标系下通过对每个颗粒进行跟踪来研究颗粒的运动，即颗粒轨道模型，可对具有各种颗粒类型、尺寸、形状和速度的流动进行分析【7】。从现象上看，颗粒轨道模型是最适合研究颗粒、流动两相系统的宏观结构，它可以给定单个颗粒的物理特性，跟踪颗粒的蒸发、挥发和反应过程，并可以考虑气体和颗粒间的耦合作用，以及颗粒间的相互碰撞行为。同时模拟计算中的颗粒并非等同于实际意义的颗粒，而是将具有相同物理性质的颗粒打包成颗粒群(称之为“计算颗粒”)，将上亿的颗粒系统进行简化，从而大大提高计算效率，为准确高效模拟气固系统中颗粒流动特性提供了可行的条件。

现代工业中的技术条件已变得越来越专业化、技术化，因此通过数值模拟了解流化床再生器内的颗粒浓度、速度及粒度分布等特性，为再生器及分离设备结构的设计与优化提供有意义的参考，对如今催化裂化工艺非常有帮助。

1 数学模型

以CPFD技术为核心【8】，采用欧拉-拉格朗日方法模拟颗粒-流体动力学，其中固体颗粒相采用离散拉格朗日数值颗粒模型，流体相采用欧拉计算网格模型，其技术方法路线如图1所示。

图1 技术方法路线

采用欧拉-拉格朗日两相模型，求解流体的基本守恒方程如表1所示。表1中的符号解释见文后。

表1 数学控制方程

2 几何模型及参数设定

2.1 几何模型

如图2所示，流化床结构主要是由气体分布器、床体、旋风分离器及料腿组成的。该装置模拟石油工业中催化裂化单元的再生系统装置，空气通过鼓风机压缩并进行缓冲，然后经过控制阀与转子流量计进入到气体分布器中，经气体分布器均匀分布并穿过整个流化床后，在流化床顶部进入二级串联旋风分离器完成初步气固分离；分离后的气相进入布袋除尘器和湿式除尘器除尘后排放，固相则沿旋风分离器料腿进入床层内进行循环利用。

为了简化计算，本文只选择流化床主体作为研究对象，其详细结构尺寸如图3所示，其中z代表浓度测量开孔高度，在浓度测量孔上下距离0.25 m各开有1个压力测量孔，高度用h表示。流化床结构为下小上大变径式，其中小径段由2个筒节组成，大径段由8个筒节组成。流化床小径段底部设有气体分布器。分布器采用管式结构，上部开口数为48个，孔径为0.006 m，如图2右下角所示。

采用Solidworks进行建模，通过笛卡尔网格划分功能对流化床进行网格正交划分，网格示意如图4所示。对流化床局部结构进行网格加密，该模型共设有702240个网格。

2.2 模拟参数与边界条件

实验中的颗粒相采用FCC催化剂，颗粒密度为2 600 kg/m3，平均直径为64.62 μm，粒度分布PSD如图5所示；气体介质为空气，密度为1.17 kg/m3,气体粘度为1.84×10-6kg/(m·s)。定义入口为速度边界条件，出口为压力边界条件，数值模拟参数如表2所示，模拟初始条件云图见图6。

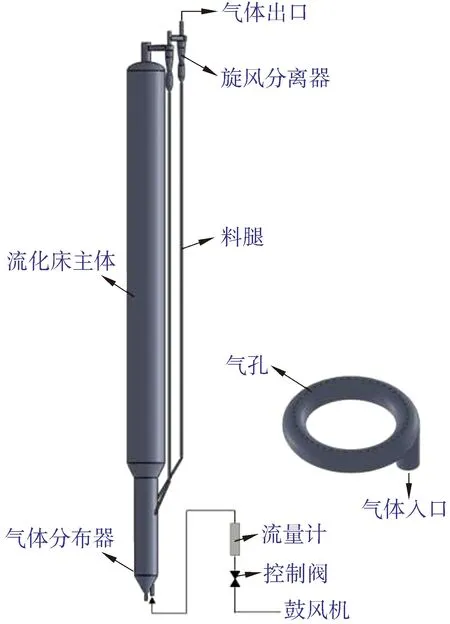
图2 流化床结构

图3 流化床几何模型

3 结果分析与讨论

3.1 模型验证

为检验采用的数学模型及使用的模拟计算方法是否准确、合理，本文沿轴向取任意8组高度差，将对应高度差下数值计算获得的压降值与实验结果进行对比，各高度差代表的具体位置见表3。图7为压降的实验值与模拟值对比。如图7 所示，任意高度差下压差的实验值与模拟值吻合较好，且整体变化趋势基本一致，由此可见该模拟方法能较为准确地反映出湍动流化床内气固两相的流动特性。

图4 流化床网格示意

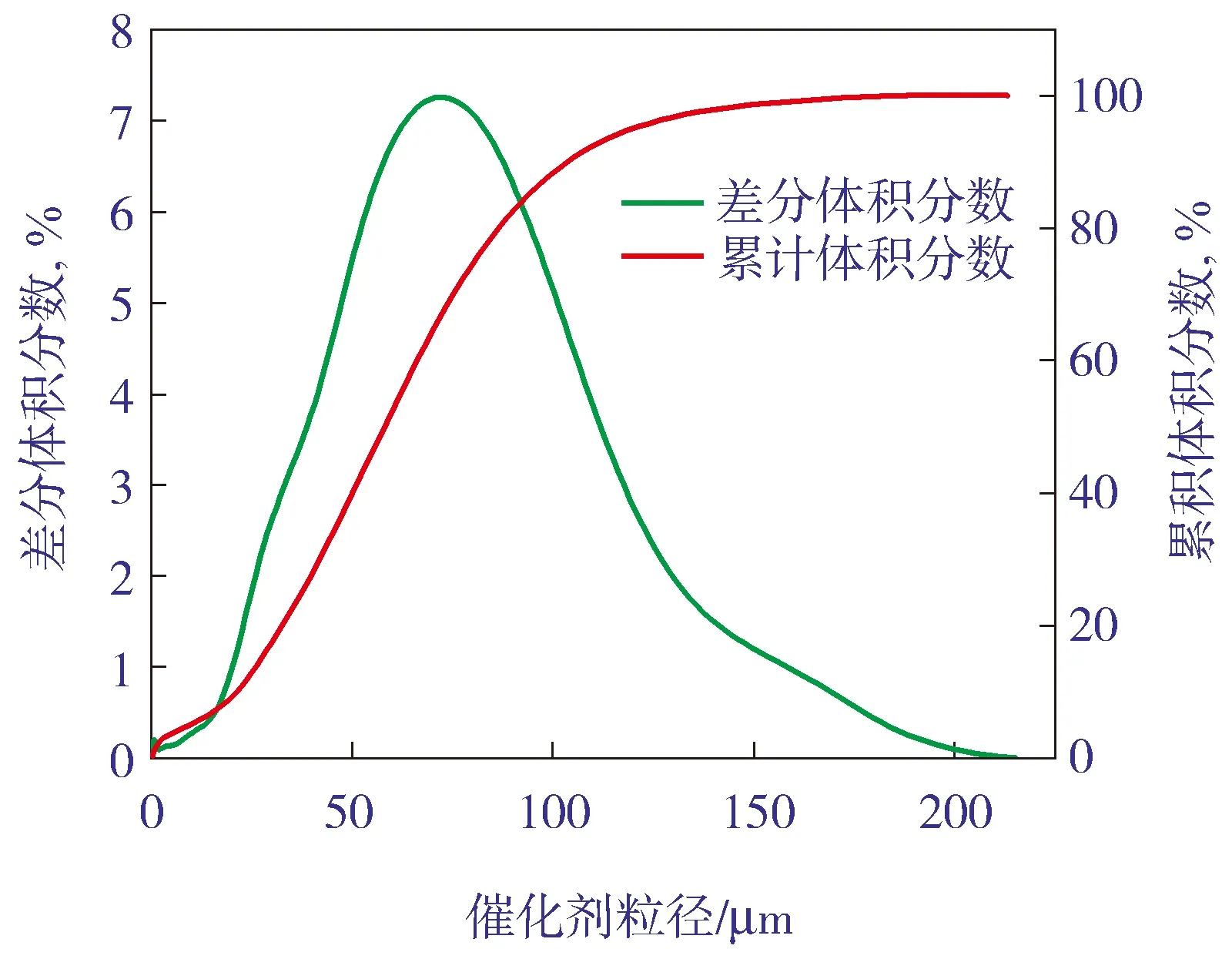
图5 催化剂粒度分布

表2 数值求解参数

通过将采用不同曳力模型获得的密相床层压降值与实验值进行对比，获得与实验情况最接近的气固曳力模型。如图8所示，模拟情况下曳力模型Haider Levenspiel与Richardson获得的密相床层压降最接近实验值，而Richardson模型仅适用于单颗粒尺寸分布的模拟，故选择Haider Levenspiel曳力模型进行湍动流化床的数值模拟。

图6 数值模拟初始条件云图

图7 轴向压降实验值与模拟值对比

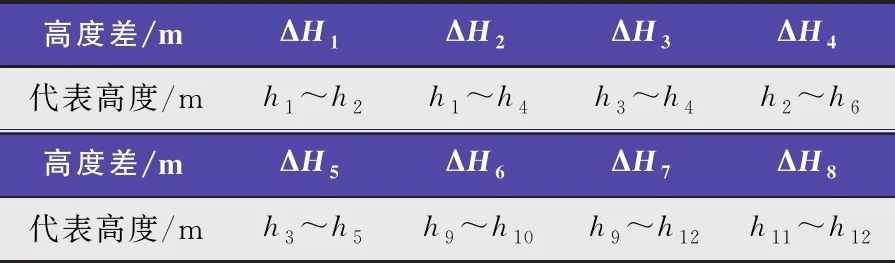
表3 ΔH代表的高度差

图8 不同曳力模型密相区压降对比

3.2 床层内颗粒流动特性分布

图9为流化床中心区域压力沿轴向的时均分布。由图9可见，中心区域的压力随着轴向高度的增加而减小，在流化床的密相段颗粒浓度高，气泡运动剧烈，所以此处压力变化较大，而稀相区及上部自由空域颗粒浓度很小，气体介质流化比较平稳，压力变化较小。

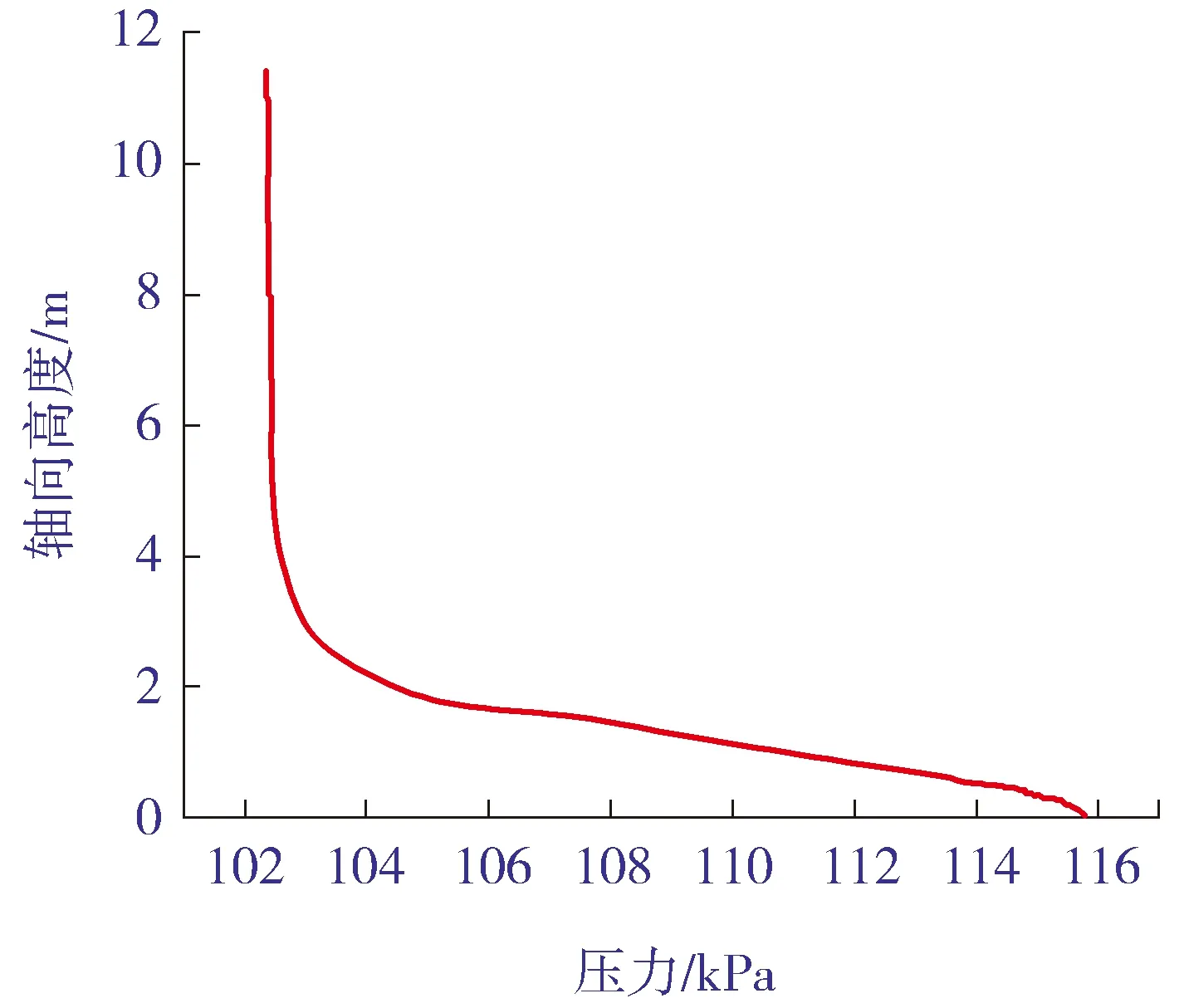
图9 时均轴向压力

图10表示湍动流化床沿轴向的时均固含率分布。由图10可见，随着轴向高度的增加，颗粒浓度呈 “ε”形分布，总体上颗粒浓度随着轴向的增高而逐渐减小。根据轴向颗粒浓度，可以将流化床分为底部密相区、中间过渡段以及上部稀相区，其中稀相区中固含率沿轴向高度不变的区域为自由空域。颗粒浓度在密相区较高，稀相区较低，而中间的波动区域则是由过渡段内存在不规则的气泡运动所造成的。

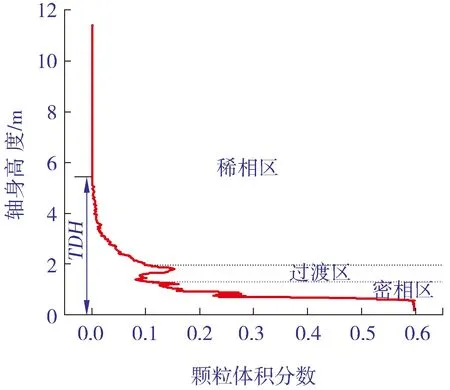
图10 轴向固含率分布

图11表示湍动流化床内沿径向的时均固含率分布。由图11可见：在轴向高度z1=3.32 m处，颗粒浓度在边壁处较高，在中心处较低。这主要是因为湍动流化床内的大部分气体都是从床层中心通过的，气体对颗粒的脉动比较剧烈，而在壁面处颗粒浓度较大便会发生团聚，所以在此处沿径向形成了“环核”结构；在z2=4.32 m处边壁处的颗粒浓度与中心处相差不大，说明此处“环核”结构已经消失，即沿轴向 “环核”结构呈现递减的趋势，直至消失；随着轴向高度的增加，颗粒浓度沿径向的分布变得更加均匀，z3=5.32 m处整个径向截面处的浓度已经十分接近。图12为轴径向固含率云图分布，图中z=2.32 m处也可明显看出边壁处的颗粒浓度较高，且总体分布规律与图11的描述一致。

图11 径向固含率的分布

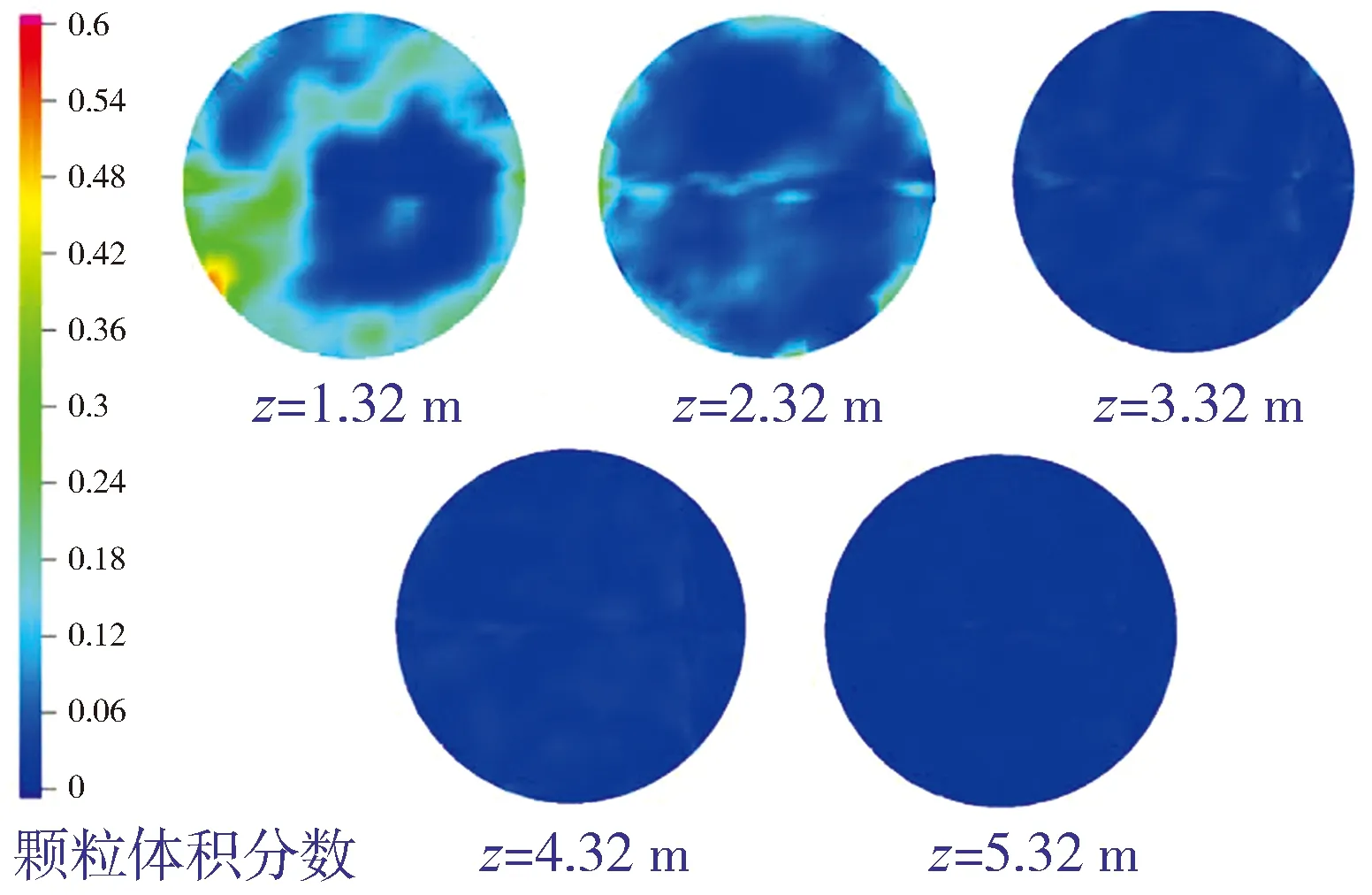
图12 轴向固含率的云图分布

图13表示湍动流化床内不同床层高度下颗粒的时均轴向速度分布。由图13可见：流化床中心区域的颗粒速度普遍要大于边壁处的颗粒速度，且随着轴向高度的增加，颗粒轴向速度在径向分布的起伏变大，但总体分布趋势相同；在轴向高度z=5.32 m处，此时颗粒处于稀相区，颗粒轴向速度从中心到边壁呈现出先减小后增大的趋势，且在中心区域附近也存在颗粒下落的情况，壁面处的颗粒不再下落，说明颗粒下落位置由壁面向中心存在移动。

图14表示湍动流化床内不同轴向高度颗粒的瞬时轴向速度分布云图。由图14可以看出：由于气泡的剧烈运动，使得分布器区域的颗粒速度产生不规则的变化；在远离分布器区域的密相区，颗粒速度明显呈现出中间高、沿壁面速度逐渐降低的趋势，且在壁面处颗粒为向下运动，所以颗粒在密相区就会形成颗粒的循环流动；而稀相区的颗粒速度径向分布相对比较均匀，在边壁处也很少出现颗粒下落的情况，但颗粒速度总体仍呈现出中心高、边壁低的趋势。

图13 径向颗粒速度分布

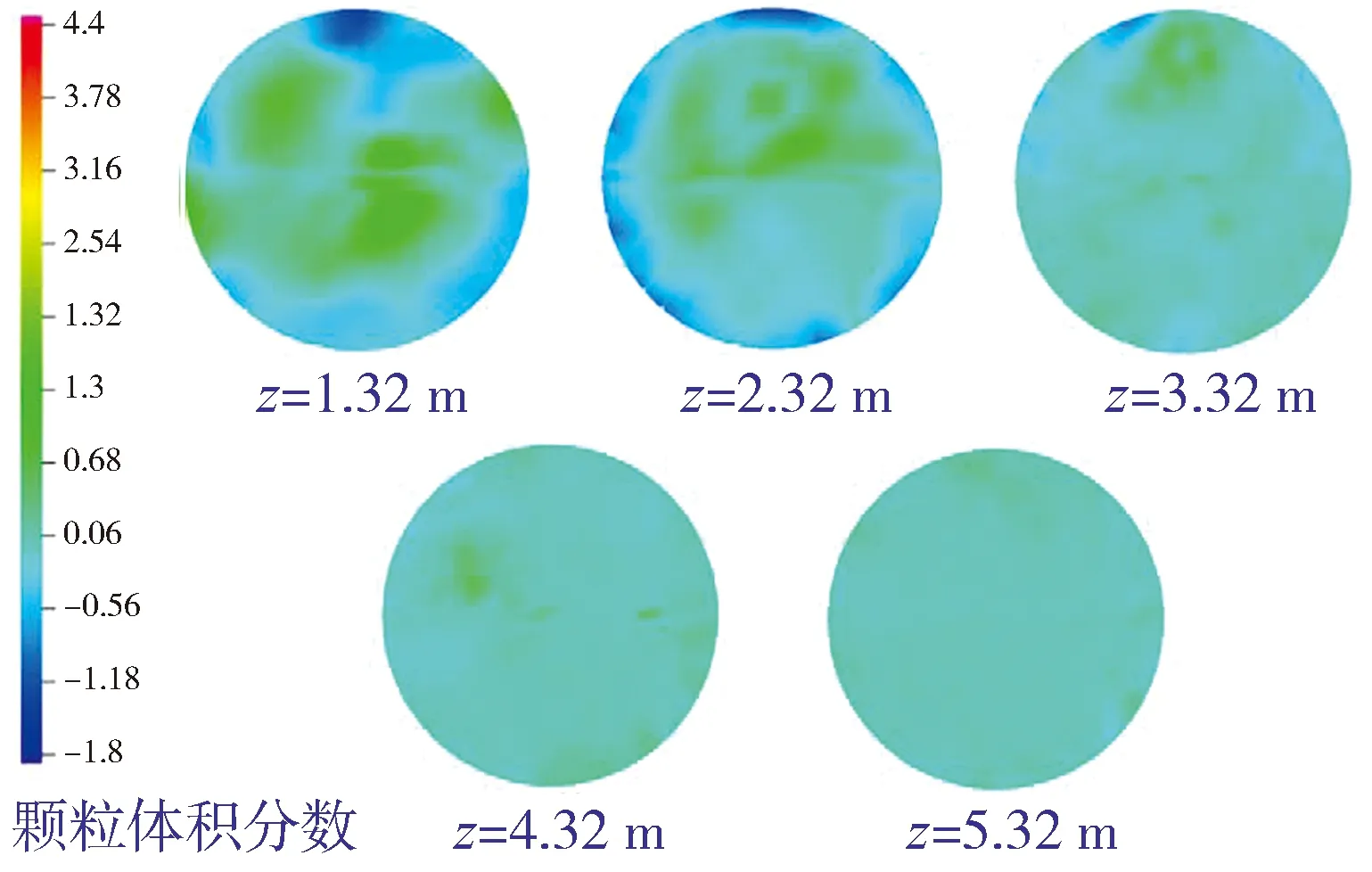
图14 径向颗粒速度的云图分布

图15表示流化床内颗粒粒径沿轴向的分布。由图15可见，颗粒粒径沿轴向高度的增加逐渐降低，在稀相区粒径分布相对比较均匀。在密相床层表面，由于气泡破裂时的夹带，使大量颗粒被抛向自由空域，而颗粒的扬析现象使颗粒在流化气体的作用下因具有不同的终端沉降速度而分级，在不同的轴向高度出现颗粒回落，较大的颗粒及颗粒团便会集中在密相区及过渡区，此处由于气泡的作用存在颗粒循环，因此颗粒在密相区及过渡区的分布相对不均匀，而较细的颗粒便存在于稀相区顶部。

4 结语

基于欧拉-拉格朗日双流体模型，采用颗粒流体动力学方法，通过数值模拟研究了湍动流化床压力、固含率、颗粒速度、粒度分布等流动特性，模拟结果表明：

图15 颗粒粒度的云图分布

1) 通过对采用不同曳力模型数值模拟获得的密相床层压降值与实验值进行对比，最终确定曳力模型Haider Levenspiel最接近实际情况。

2) 湍动流化床中心区域的压力随着轴向高度的增加而减小，在密相段压力变化较大，而稀相区压力变化较小。

3) 根据流化床内轴向颗粒浓度的分布，可以将床层分为底部密相区、中间过渡段以及上部稀相区，中间的浓度波动区域是过渡段内存在不规则的气泡运动所造成的；在密相区上部，颗粒浓度沿径向呈现中间高、边壁低的“环核”结构，且该结构沿轴向高度逐渐减小，直至消失。

4) 流化床中心区域的颗粒速度普遍要大于边壁处的颗粒速度，且随着轴向高度的增加，颗粒速度在径向分布的起伏变大，但总体分布趋势相同；在稀相区上部，颗粒下落位置由壁面向中心存在移动。

5) 颗粒粒径沿轴向高度的增加逐渐降低，在稀相区粒径分布相对比较均匀。

符号说明

t——时间，;

m——颗粒质量，kg;

εg——气相体积分数;

p——气相压力，Pa;

ρg——气体密度，kg/m3；

F——单位体积内气固两相动量交换律;

ug——表观气速，m/s；

g——重力加速度，m/s2;

τg——气相应力张量，Pa；

D——相间交换系数；

Dp——曳力系数;

f——概率分布函数；

up——颗粒速度，m/s；

εs——单位网格内颗粒体积分数;

ρp——颗粒密度，kg/m3；

Xp——颗粒位置向量;

εp——固相体积分数；

τp——颗粒法相应力，N;

mp——颗粒质量，kg；

μf——流体粘度，kg/m·s；

rp——颗粒半径，um；

Re——雷诺数；

Vp——颗粒体积，m3；

FD——气固相间曳力，N；

fh——与雷诺数相关的参数。