谷歌打造开放源码库RLiable让机器强化学习评估更可靠

强化学习作为机器学习的三大基本范式之一，被用在诸多学科，如信息理论、基于仿真的优化、多智能体系统、群体智能、统计学等。

强化学习通过从经验中学习来解决决策任务，其重点是在探索未知领域和开发现有知识之间找到平衡，涉及智能代理应如何在环境中采取行动，以最大限度地提高累积奖励。

强化学习已在电子游戏、平流层飞行气球和设计硬件芯片等复杂的任务上取得了可观的实验结果。然而，谷歌认为现行的强化学习经验评估标准越来越表现出一些问题，可能会给人一种机器学习在快速进步的错觉，同时会减慢强化学习领域的发展速度。

针对这个问题，谷歌在NeurIPS 2021上的一份口头报告《基于统计边缘的深度化学習》中，深入探讨了如何在只使用少量训练的情况下，考虑结果的统计不确定性，并使深度强化学习的评估更可靠。

谷歌提出了一个更严格的强化学习评估方法，并发布了多种统计工具，包括分层引导置信区间、性能概况、四分位数均值和最优性差距， 同时还发布了一个开放源码库RLiable。

强化学习中的经验研究依赖于评估一系列不同任务的表现，例如，使用Atari 100k游戏来评估进展。大多数深度强化学习算法是以比较海量任务上的相对性能进行评估的，它们得出的结果比较了总体表现的点估计值，如任务的平均值和中位数。

但不同训练运行的得分具有随机性，因此只报告点估计值并不能表明新的独立运行也会得到相似的结果。少量的训练运行，再加上深度强化学习算法性能的高可变性，往往导致此类点估计的统计不确定性很大。

随着基准测试逐渐复杂，任务的解决需要更多的计算和数据，对多次运行的评估将变得越来越困难。

因此，要想减小在计算要求高的基准上的统计不确定性，评估更多的运行不是一个可行的解决方案。

虽然以前将统计显著性测试作为一种解决办法， 但这种测试本质上是“ 二分法”的， 也就是要么“ 显著” ， 要么“ 不显著”，而简单地认为不显著的结果表明“没有关联”是毫无根据的，它们通常缺乏产生有意义的见解所需的“粒度”。

下面简单介绍下谷歌对强化学习进行更可靠评估所使用的工具。

任何基于有限次数运行的综合指标都是一个随机变量。考虑到这一点，谷歌建议使用报告分层的引导置信区间。这能够预测在不同运行中重复同一个实验时可能出现的聚合度量值。

在统计中，CIs是未知参数的一系列估计值，它可使我们理解结果的统计不确定性和再现性。

例如，在Atari 100k上对3个运行进行评估，每个运行包含26个任务，产生了78个用于不确定性评估的样本分数。在每个任务中，彩色球表示不同运行时的得分。

大多数深度强化学习算法在某些任务和训练运行中表现得更好，但是总体性能度量标准可能会掩盖这种变化，可参见下图。

谷歌对此推荐使用性能配置文件，其通常用于比较优化软件的解决时间。使用这些配置文件可以一目了然地对分数进行定性比较，当一个算法的曲线高于另一个算法时，就意味着这个算法要更好。

尽管性能配置文件对定性比较有用，但在算法方面却稍逊一筹，以致它们的图像经常相交。因此，为了更好地进行定量比较，需要总体性能指标。

然而， 现有的度量标准存在一些局限性，比如，单个高绩效任务可能支配任务平均得分;近一半任务的中位数不受零得分的影响，并且在较小的统计不确定性下需要大量的训练运行。

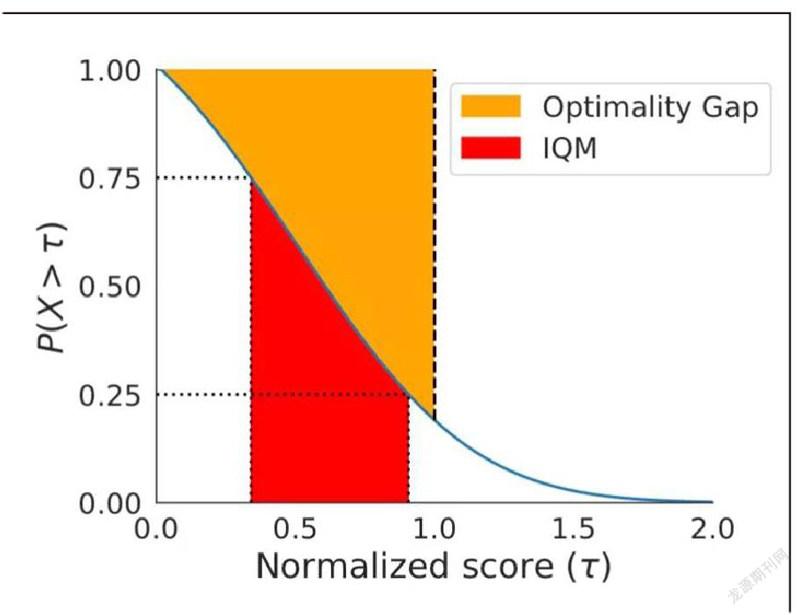
为了解决上述问题，谷歌想了两个基于稳健统计学的替代方案，四分位数均值和最优性差距，两者表示的区域如下图所示。

作为中位数和平均数的替代，四分位数均值对应于所有任务中50%的运行总和的平均得分。它对异常值比平均值更有效，是比中位数更好的总体性能指标，并且导致较小的CIs，也需要较少的运行来改进。平均数的另一种替代方法最优性差距，测量的是算法达到最优性能的距离。

为了直接比较两种算法，还需要考虑一个改进的平均概率指标，这个指标描述了改进超过基线的可能性，其计算使用的是曼—惠特尼U统计。

运用上述评估工具，谷歌在对现有广泛用于强化学习的算法进行重新审查，还发现这些评估算法中有一些自相矛盾的地方。例如， 在广泛认可的强化学习基准Arcad eLearning Environment（ALE）中，算法的性能排名随聚合度量的选择而变化。而在连续控制基准DM Control中，大多数算法的平均标准化分数在95%的CIs中存在大量重叠。

最后，谷歌希望研究人员能够通过开源库RLiable整合这些评估工具，以避免不可靠结果对强化学习的影响。