三维稳定渗流的非线性复合单元高斯点求解分析
2021-01-19张晓旭
张晓旭
(齐齐哈尔市龙沙区农业综合服务中心,黑龙江 齐齐哈尔 161000)
1 绪 论
土石坝渗流、坝基渗流、边坡渗流等地下水运动现象都是渗流的非线性问题,其本质为渗流自由面随外界环境因素的不断改变,造成相应的渗流场变动。要对渗流的非线性问题进行正确求解,重点在于渗流边界的确定,在数学迭代稳定的同时准确快捷的找出渗流自由面[1]。中国近年来渗流非线性问题理论成果众多,有限单元法、网格法、饱和方法等,该问题在实际运用中得到实质解决。
2 三维稳定渗流场数学模型[2]
三维稳定渗流场的模型原理表达式为:
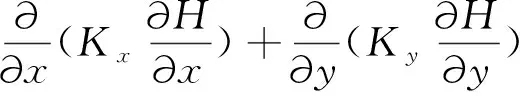
(1)
式中:Ω为渗流区域;H(x,y,z)为水头分布函数;Γ1为第一类边界;Γ2为第二类边界;Γ3为渗流自由面边界。
三维问题将计算域离散单元变换可得空间8结点等参元。坐标变换关系式如下:
(2)
单元插值函数为:
(3)
三维八节点等参元示意图,见图1。
3 算例分析
3.1 算例1
3.1.1 计算过程
该算例简化一土石坝为三维均质各向同性坝,坝宽10m,上、下游水为10m和2m。坝型简易图,见图2;有限元网格划分图,见图3。
边界条件:AE为固定边界,Y向流量为零[3]。
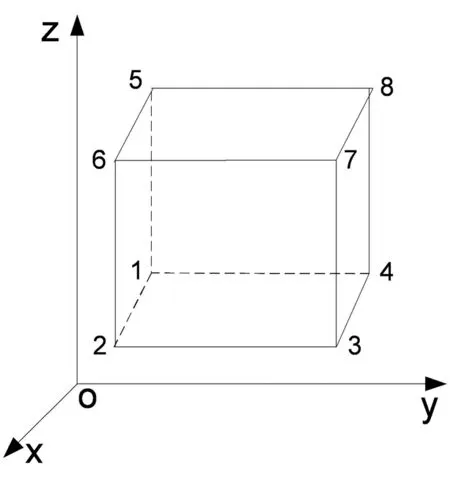
图1 三维8结点等参元
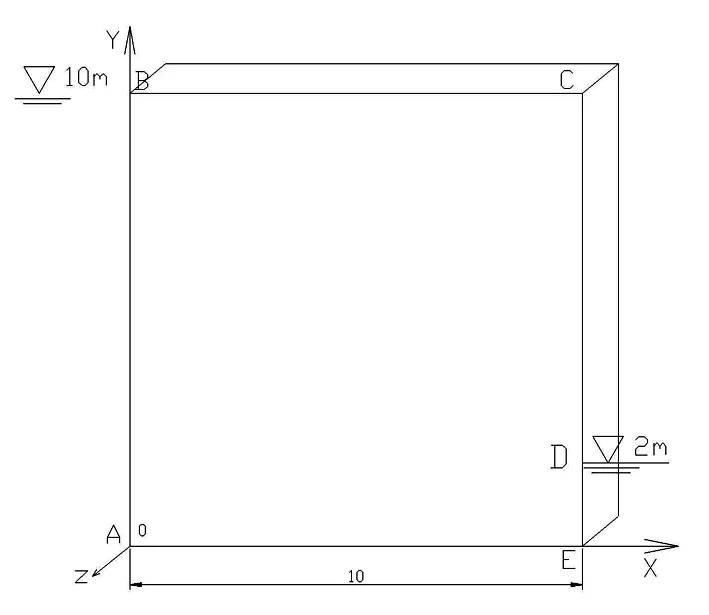
图2 坝型简易图
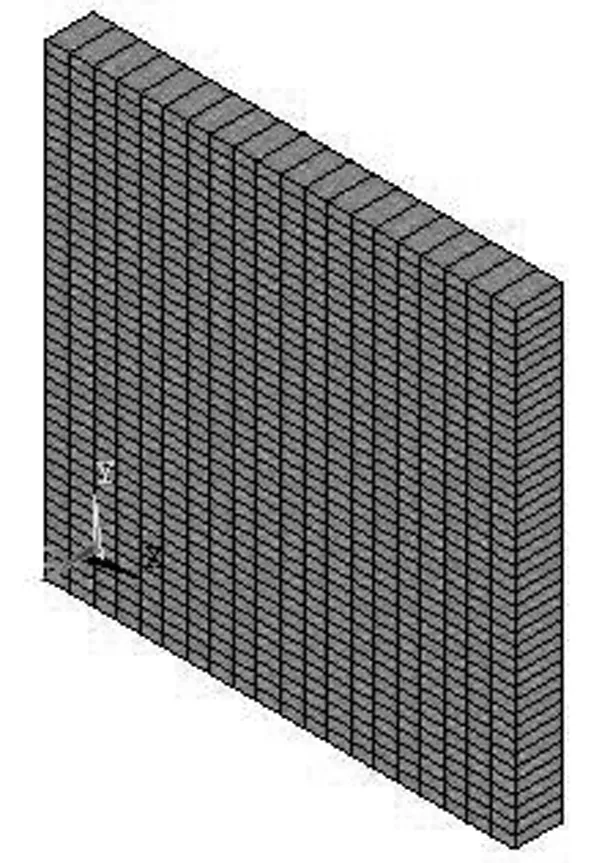
图3 有限元网格划分图
迭代15次后,计算得出横向1m的典型断面溢出点高程为4.53m。渗流自由面位置的结果比较,见表1;渗流自由面,见图4;水头计算结果,见图5;单元中心位置流速矢量结果见图6。

表1 渗流自由面位置的结果比较
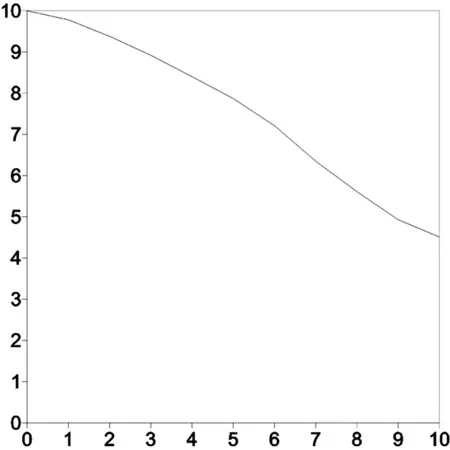
图4 渗流自由面
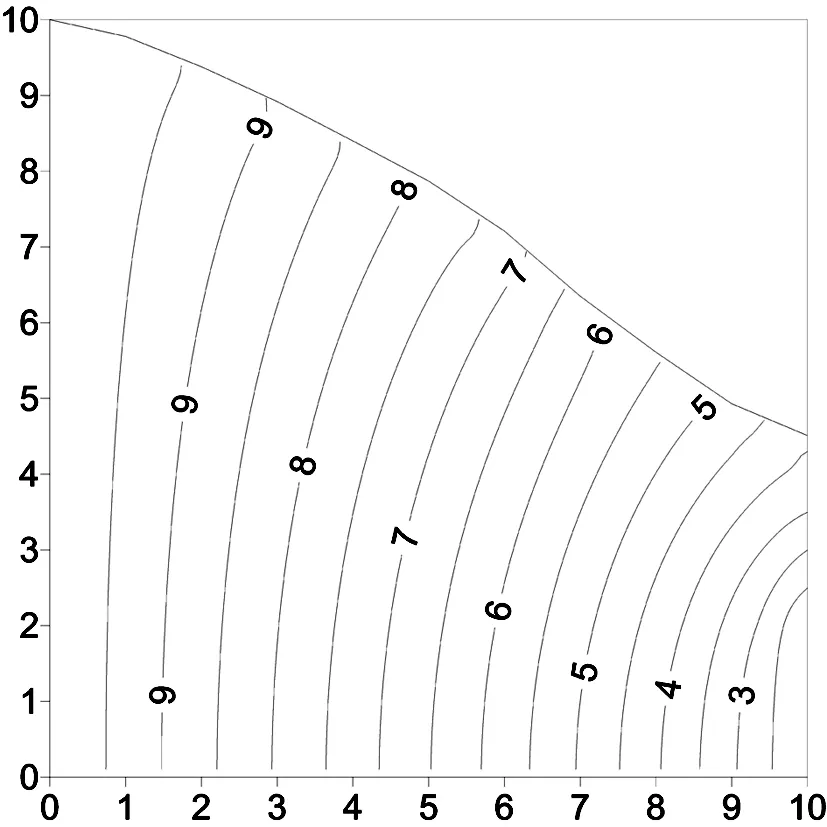
图5 水头计算结果示意图
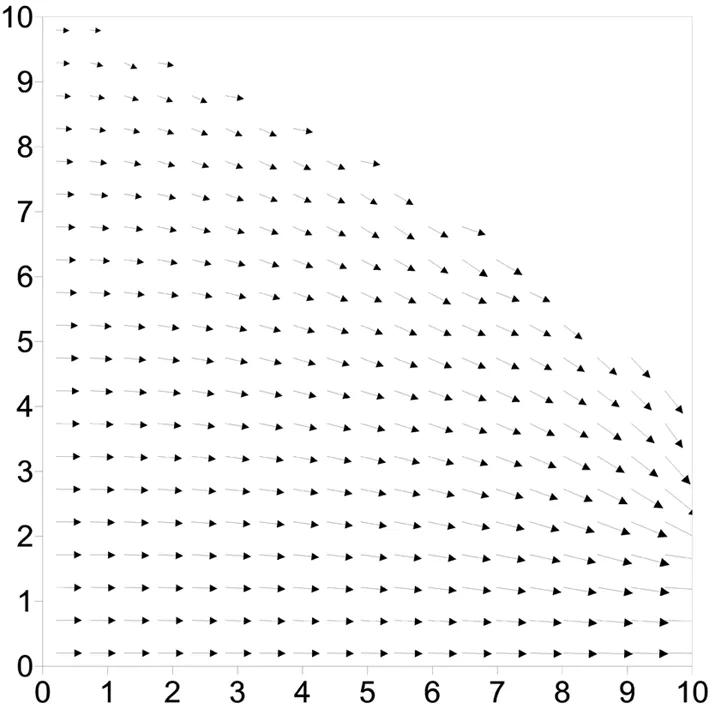
图6 单元中心位置流速矢量图
由表中结果可得,3种计算方法的渗流自由面保持一致,溢出点位置基本重合。虽溢出点位置的自由面出现局部偏差,总体结果和实测值相差较小,验证李自编程序计算非线性复合单元高斯点法是合理的。
3.1.2 稳定性分析
复合单元高斯点法早迭代时稳定性较差,局部渗流面区域出现震荡,分析该震荡产生机理表现[4],震荡现象出现原因示意图,见图7。
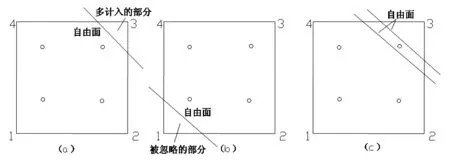
图7 震荡现象出现原因示意图
由图可得,在图1中的复合单元所有高斯积分点的水头值大于横向变形值,见图(a),该单元存在部分非饱和区,其不再是复合单元,结果中结点实际增加3结点的单元渗透矩阵作用,造成计算结果和实际相差较大。在图2中,若单元高斯积分点的水头值均小于横向值,该单元因存在部分饱和区,也不是复合单元,结果中易忽略1结点的单元渗透矩阵作用,同样不符合实际。在图3中,自由面在高斯积分点在渗流自由面的细小改变,积分值均会产生较大改变。
3.2 算例2
本算例在上节计算程序的基础上做出变动,目的是为实现高斯点加密后的单元功能,更好体现复合单元高斯点模拟效果,增加各坐标轴的高斯点至18个[5],计算可得加密后的渗流自由面位置。高斯点加密前后的的渗流自由面,见图8。
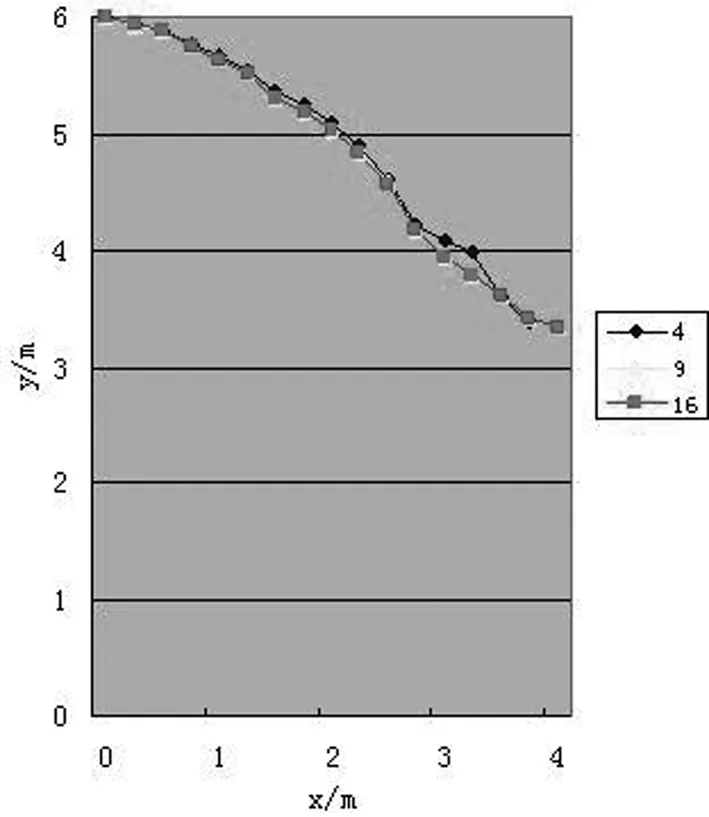
图8 高斯点加密前后的的渗流自由面
由图可知,当高斯点数目为10个,渗流自由面的局部较大偏差显著减少,当高斯点数目为18个,渗流自由面已趋于稳定,未发生改变,表明在本算例的有限元网格划分基础下,复合单元高斯点法的求解已稳定,通过加密高斯点可有效提高渗流自由面的稳定性,其数值解亦能最大程度得到稳定。
4 结 论
文章在三维稳定渗流原理和数学模型基础上,结合工程算例建立有限元模型,基于复合单元高斯点法求解连续介质渗流非线性问题,对比不同高斯点数目下的渗流面位置稳定性,形成高斯点法求解渗流非线性的稳定性探讨,对比计算值和实测值,验证自编有限元程序的合理可行性。
