基于蒙特卡罗方法的水体光场传输特性研究∗

（海军驻武汉地区第七军事代表室 武汉 430223）

1 引言

进入21世纪，随着经济和技术的快速发展，对海洋的研究已经成为一个新的领域。海洋资源开发、海洋自然环境保护以及海洋军事应用等方面的研究越来越引起人们的关注［1］。

光电探测成像技术是海洋探测及环境保护的重要手段之一。然而，光在水下传播过程中，受到水分子和其他悬浮粒子的作用，将发生吸收和散射现象，使得光线能量逐渐衰减，且成像质量急剧下降。因此，对水下光场传输特性的研究具有重要的意义［7］。

研究水下光场传播规律的主要方法有几何光学方法、辐射传输方程方法［3］和蒙特卡罗模拟方法等［4～5］。几何光学方法主要是采用光在水空界面的折射定律和光在纯净水中的直线传播规律，无法深入研究散射背景条件下的光传播特性。辐射传输方程虽然可以描述光在强散射水体中的传播特性，可详细地考虑散射、吸收、辐射等光与物质相互作用的现象，但是对于复杂边界条件和初始条件下方程求解比较困难。而蒙特卡罗模拟方法［6～9］作为研究散射介质中光传输特性的一种适用广泛而严谨的方法。本文基于该方法仿真分析了在强散射背景条件下水体的光场传输规律。

2 方法

光子在水体中的传播规则采用概率分布来描述。如图1是蒙特卡罗方法水体散射仿真流程图，单个光子首先被初始化统一权重，设置光子步长，并在坐标系中移动它。

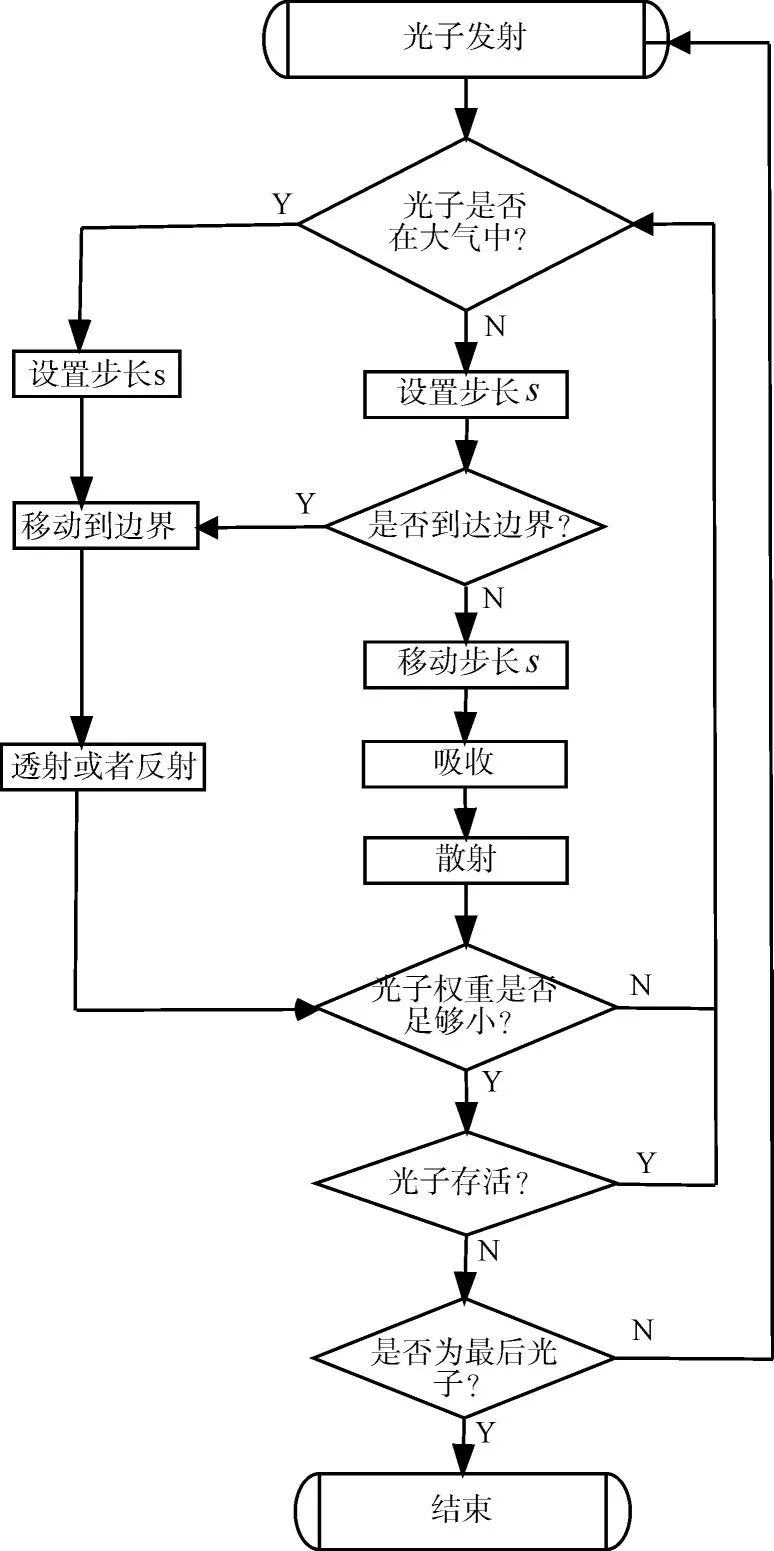
图1 蒙特卡罗方法水体散射仿真流程图

若光子到达水体边缘，检查其内部反射的几率，并决定其是继续留在水体内还是离开水体。若其在内部反射，则需修改其运动方向，继续运动；否则，光子离开水体，记录为反射（透射）。在每运动一个步长，计算光子由于水体的吸收造成的权重衰减，并记录在该处水体吸收矩阵中。剩下的光子权重代入到散射后移动方向传输步长计算中。若光子权重低于一定小的阈值，则执行轮盘赌算法来决定忽略此光子或继续计算它的移动。

2.1 光子的初始化

每一个光子在最初统一设定一个权重W。当光子在水体边界遇到折射率改变界面时，会发生镜面反射。设入射空气折射率为n1，水体折射率为n2，则镜面反射率 Rsp为

则光子的权重被减去Rsp。

2.2 光子步长

根据吸收系数和散射系数的定义，光子与水体介质在单位步长［s1，s1+ds1］内相互作用（包括吸收与散射）的几率为μ1ds1。由水体的比耳朗伯定律［4］可得:

其中，μa为吸收系数，μs为散射系数，μt是总衰减系数，单位是m-1。对上式进行变换，在［0，s1］内积分，得到指数分布:

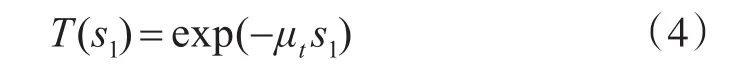
表示光子步长大于 s1的几率，即P｛s≥s1｝。对于自由路径s的累积分布:

变换上式求解得到:

设定ζ=P｛s＜s1｝，且在（0，1］区间均匀分布，因此ζ与1-ζ的分布相同，则-ln（1-ζ）与-ln（ζ）等价，故:

依此式，在（0，1］区间内生成随机数ζ，便得到步长s=s1。

2.3 光子移动

当s被确定以后，光子就可以在坐标系中移动。设光子的瞬时位置为（x，y，z），瞬时方向单位向量r，可表示为（μx，μy，μz）:

在移动后光子的位置为（x’，y’，z’），则:

2.4 边界处理

在光子移动一个步长过程中，光子可能会遇到水体边界。当光子遇到边界时，光子可能反射（或透射）逃逸出水体或者向内部反射。光子向内反射的几率取决于入射到边界的角度（θi）。可计算得到:

由Snell公式表示入射角θi与折射角θt的关系。向内反射的几率R（θi），可由Fresnel公式得出:

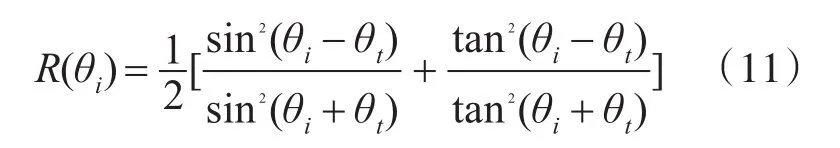
因此，1-R（θi）表示光子离开水体成为反射部分，计入反射矩阵。

在光子离开介质前，只行走了步长s的一部分。因此，实际离开位置应该是基于减短的步长s':

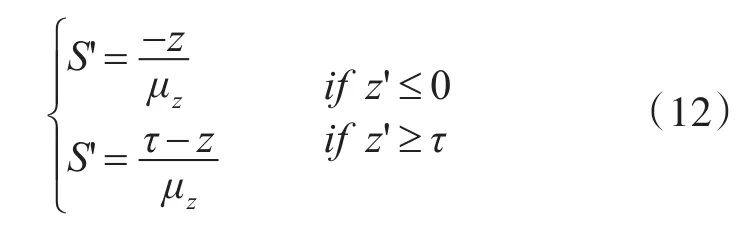
其中τ表示水体的厚度。若光子内反射，则光子权重计算为

剩下的光子有新的位置和方向。x，y坐标可直接用前述公式计算，z坐标更新为

2.5 光子吸收

当光子移动一定步长时，光子由于水体介质的吸收，会使得权重减小。权重减小的幅度ΔQ:

光子权重W更新:

由于（μa/μt+μs/μt）=1，因此能量是平衡的。

2.6 光子散射

当光子发生散射时，光子的轨道偏转角度θ分布在［0，π］。Henyey与Greenstein［10］最早提出利用散射相函数来计算散射偏转角的概率密度方程:

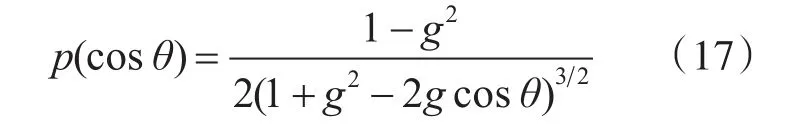
其中，g为各向异性因子，表示散射的角度分布。令μ=cosθ，分布在［-1，1］。可以推导出:

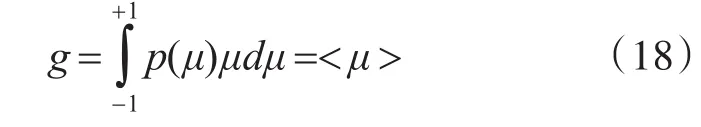
因此，g表示介质中散射角余弦的平均值。各向异性因子g取值在-1～1之间。

计算出偏转角和方位角，新的光子轨道μ′x，）则可从旧的轨道（μx，μy，μz）和偏转角θ与方位角ψ计算得到:

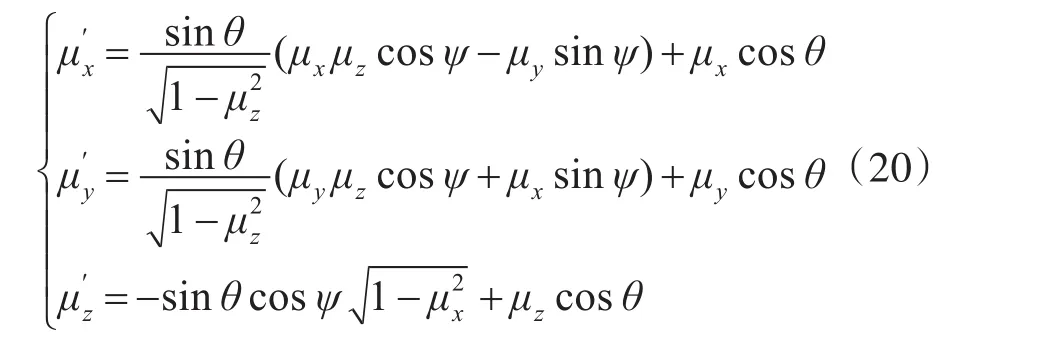
2.7 光子终止

若光子的权重衰减到足够小，并低于一定阈值时，那么它的传输对计算结果的影响将可忽略。为了减小忽略权重而带来的误差。采用轮盘赌方法对权重小于阈值W的光子进行处理。在一定数量m的光子中让其中一个光子能够存活下来，并使权重增为mW，其他的光子则为0。

3 结果

3.1 水体参数设置

根据实际水体所满足的参数和成像探测范围，选取深度为30m，半径为5m的圆柱形水体区域，网络划分的精度为0.01m，进行蒙特卡罗程序仿真实验，如图2所示。设从水体的吸收系数为0.2 m-1，散射系数为 0.1 m-1，各项异性因子为 0.8［11～12］。为了保证一定的仿真精度，选择入射光子包数为100万。

图2 水体介质模型示意图

3.2 单光子散射路径

根据仿真设计的参数，首先分析单光子的散射路径，并对单光子的散射路径和散射方向进行描述，如图3所示。部分单光子经过了水体的折射、散射和吸收后，最终又在水面出射（如图3中上面三图所示）；部分单光子经过水体折射、散射和吸收后，最终被吸收掉（如图3中左下图所示）；部分单光子进入水体后，直接在通过水体出射（如图3中右下图所示）。

3.3 水下光子密度空间分布

将100万个光子在规定的水域中心位置，准直入射到水体中，光子经过水体的反射、折射、散射和吸收，并对100万个光子能量进行统计，可以得到不同位置的光子密度空间分布和不同位置的光子密度空间分布等高线图，如图4所示。Colorbar采用jet颜色映射［13］，表示以10为底的光子数对数大小。

图3 单个光子在水体中的散射路径

图4 光子密度空间分布仿真图和高线图

3.4 不同深度下径向光子密度分布

根据仿真数据，进一步对比统计分析了在水下不同深度时，光子密度（或光子数）的径向分布，如下图所示。分别统计了水下深度为5m、15m和25m处的光子密度，其对数分布曲线如图所示，可以看到光子密度随着深度增加，光子密度整体上成递减趋势，但是在距离入射位置处光子密度比远离入射位置处的值要大。在深度为25m时，光子密度已经非常低，达到10-4。

3.5 不同深度下散射光子分析

透过水体的光子可以分为弹道光子和散射光子，散射光子可以分为蛇形光子和扩散光子。一般地，认为弹道光子在传统透镜式成像中起到了主要贡献，而散射光子是被水中散射子散射的光子，对成像起到干扰作用，为噪声成分。

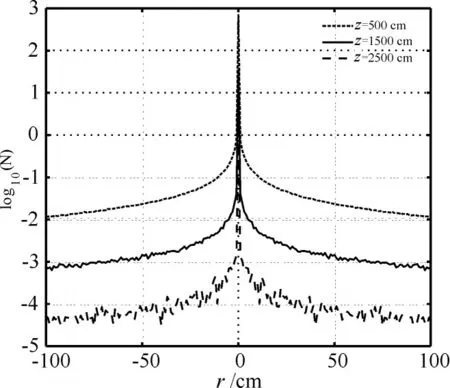
图5 不同深度下光子数径向分布

图6 不同深度下，弹道光子去除和未去除透射光照度对比

为了对比分析不同水体深度下，弹道光子去除和未去除时对透射光子密度分布影响，分别对水深度为2m、6m、10m和15m的水体仿真研究，其对比图如图6所示。在每个水体深度下，左上图是未去除弹道光子的透射光子密度分布图像，左下图是未去除弹道光子的透射光子密度分布图像对应y为0位置的光子密度分布（Colorbar以光子密度的对数形式表示出），右上图是去除弹道光子的透射光子密度分布图像，右下图是去除弹道光子的透射光子密度分布图像对应y为0位置的光子密度分布。其他水体深度，同理可得到如图4所示。

由图中可以看出，未去除弹道光子时x为0位置处的光子密度数远大于去除弹道光子时，但是随着深度增加，其比值会逐渐减小，说明散射光子在深度比较小时对成像影响比较小，但是在水体深度比较大时，弹道光子较少，散射光子也会减小，值得注意的是，弹道光子减小的比例比散射光子减小的比例要大。所以在大深度区域成像时，主要贡献的直行光子会被噪声淹没，无法进行成像。

4 结语

本文基于蒙特卡罗仿真思想设计了水下光场传输的蒙特卡罗程序算法，选取实际水体参数，对水下单光子散射路径、水体光子密度分布、不同深度径向光子密度分布和不同深度下散射光子影响进行了仿真分析。单光子路径主要有三种情况:直接透射、最终出射水面、最终吸收。光子包垂直进入水中时，弹道光子密度数远大于散射光子时，但是随着深度增加，其比值会逐渐减小，说明散射光子在深度比较小时对成像影响比较小，但是在水体深度比较大时，弹道光子减小的比例比散射光子减小的比例要大。所以在大深度区域成像时，起主要贡献的直行光子会被噪声淹没，无法进行成像。