基于蒙特卡罗法的海上落水遇险人员漂流轨迹预测∗

2021-01-19

舰船电子工程 2020年12期

（海军航空大学青岛校区青岛 266041）

1 引言

随着综合国力的增强和科学技术的进步，“辽宁号”航母列装，我国海军从浅蓝走向深蓝，舰载机飞行员完成航母起降训练，是我国国防力量增强的表现。因此为保证战斗力、保障生命，对人员落水后及时、快速的搜寻，是我国目前海上航空搜寻研究的重点课题。

对海上遇险落水人员的搜寻基础是预测漂移轨迹，国内外许多学者都对海上漂浮物的漂移特性都进行了细致的实验和研究。从20世纪80年代起，在军事需求实用化的推动下，针对航空遇险，搜索理论进入以运动目标为搜索算法的研究时代，Brown设计了运动目标探测算法方面，Allen A和Plourde J.V等系统性研究了在海上风压作用下漂浮物的运动特性，Ohsumilss用一个扩散过程来描述目标的运动，Breivik采用了蒙特卡洛算法确定搜寻区域。国内大连海事大学等高校系统性的对海上搜寻做了的建模仿真。这些模型是基于解析法设计的，整体误差过大［1～2］。本文以海上遇险人员对研究对象，采用蒙特卡罗法预测落水人员的漂移轨迹。

2 漂移数学模型建立

海上遇险人员落水分为无速度和有初速度两种情况，航空人员海上遇险由于弹跳开伞等原因，一般在水平方向有初速度。不考虑落水前弹射离机的位移，针对落水后的研究漂移情况，因海水密度较大，在不考虑垂直作用力的情况下，落水人员受风力、海浪、流速三种力的共同影响下在海面上做水平漂移。经实验研究表明［5］，当落水目标长度小于50m相对于海浪波长较小时，可以忽略波浪对落水目标的影响。因此相对于海上落水人员而言，漂移速度主要受到风力与流速两方面因素的影响，即是暴露于海面上的身体部分所受到的风力漂移、浸渍在海面下的身体部分所受到的流速漂移两方面因素影响［1，9］。设定人员落水初速度为v0（v0可为0），风力漂移速度为vw，采用海面下0.5m处的流速漂移速度vf，则落水人员的漂移速度v表示为

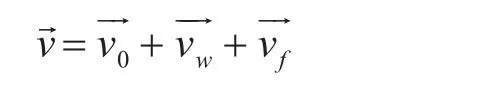
根据落水人员的受力分析可知漂移运动方程为

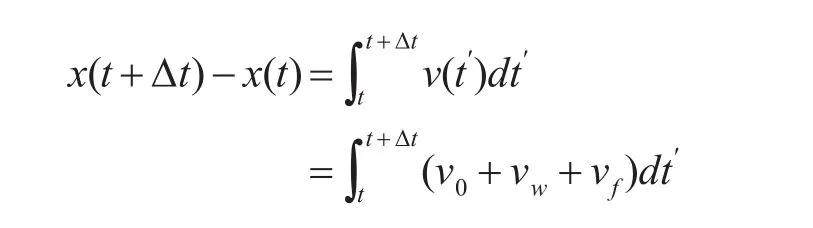
在运动方程中v0为飞行员跳伞着陆速度，允许垂直着陆的耐限值是10.7m/s［14］，水平速度受降落伞阻力和海上风力共同影响，因此风力漂移在运动方程中起决定作用。

3 风力漂移模型

风力漂移是由于落水人员暴露于海面上的身体部分受到风压作用引起的，可以分解为顺风分量DWL和侧风分量CWL，如图1所示。从风力漂移速度到顺风分量的夹角为风压角α，风压角α可以在风速顺时针偏右方向，也可能是在风速顺时针偏左方向，这里定义在风速方向顺时针偏右的侧风分量为正，偏左为负。

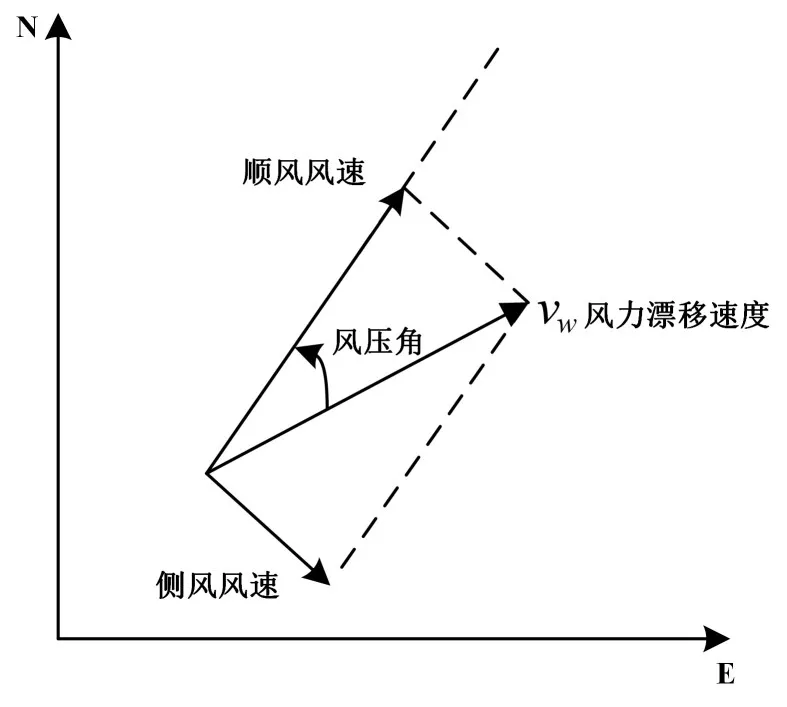
图1 风力漂移速度分解模型

风力漂移速度受落水目标大小、形状、海面上下面积比等多方面影响，本文针对目标为落水人员，选用Allen Plourde等对不同类型搜寻目标的风压试验数据结果，确定落水人员于海面上空10m处风速的关系。模型顺风分量风压经验值与海面上空10m高处风速关系如图2所示，当风压模型速度为0时，顺风分量也为0，随海上10m处风速增大，顺风矢量也增大，但存在一定的误差。

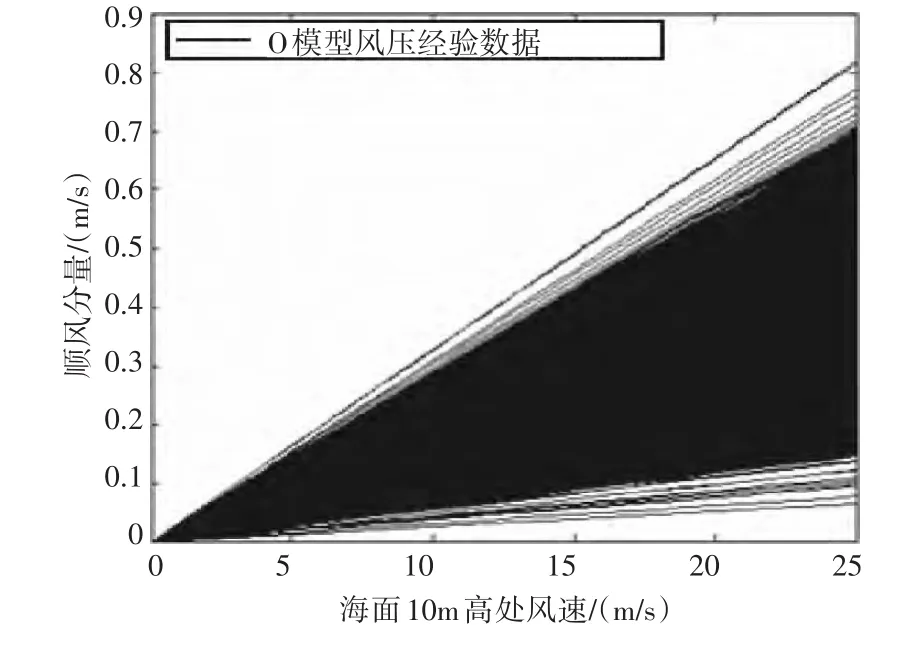
图2 模型顺风分量风压经验值与海面上空10m高处风速关系

风力漂移模型是在现有的经验数据上增加约束条件统计回归计算得到的，顺风方向风压矢量、侧风方向风压矢量与海面10m高出风速之间的线性回归方程为

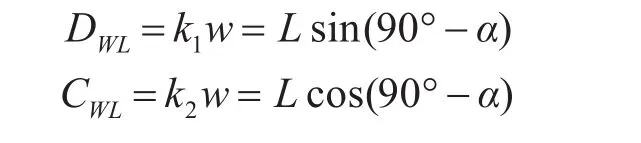
式中:w为风速矢量；L为总风压矢量；α为风压角；k1为顺风向风压系数；k2为侧风向风压系数。

漂浮物的漂流速度记为Vd应满足:

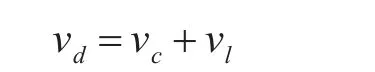
式中:vc为海流对地总流速；vl为漂浮物相对水面环境的速度，即风压速度。

人员落水漂流的即时位置POSc应满足:

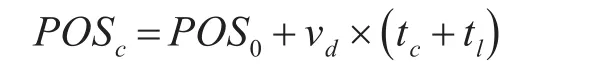
式中:POS0为事发位置；tc为当前预测时间；tl为事发时间。

4 流场数据插值算法

为减小对目标漂移预测的误差，需要提高流场数据的精确度。在流场计算过程中一般是使用插值函数来描述内部各个点的值。插值法是在一直的函数表中，插入一些表中有没列出的所需要的中间值的方法。主要有线性插值法、图解内插、多项式插值、差分插值法、分段插值等是数学算法，根据插值多项式余项公式表明插值节点越多，误差越小，函数逐近越好，但是插值多项式的次数过高，会产生Runge现象，即出现误差不降反增的现象，因此为更精确地描述内部各点值，本文采用分段线性插值法。

设插值节点为xi函数值为yi，i=0,1,…,n，hi=xi-1-xi，i=0,1,…,n-1，h=maxhi，任取两个相邻的节点xk，xk+1，形成一个插值区间[xk,xk+1]，构成Lagrange线性插值。插值多项式L1(x)可表示为

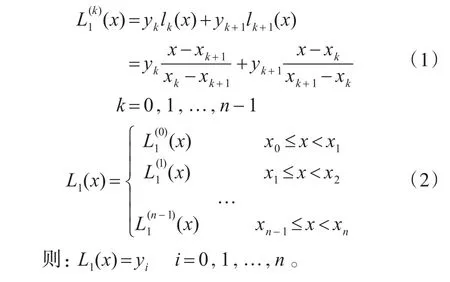
5 实验及实例分析

5.1 实验方法

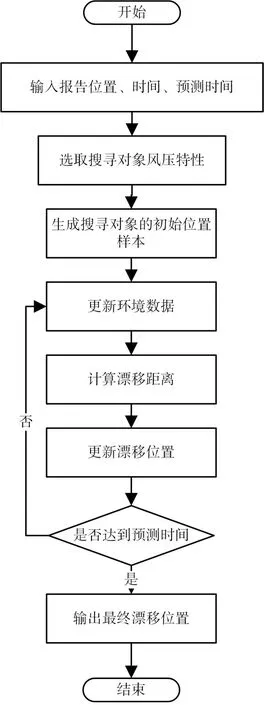
图3 算法流程图

蒙特卡罗（Monte Carlo）法是也称统计模拟方法，是由于科学技术的发展和电子计算机的发明二备提出的一种以概率统计理论为指导的数值计算方法，其基本思想是当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种实验的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的数字特征，并将其作为问题的解。基于此将落水人员抽象成粒子并大量复制，认为对每个粒子都因海洋环境的作用而产生漂移，通过描述这些粒子出现的位置概率来预测落水人员的漂移轨迹。考虑粒子在漂浮过程中t+1时刻所处的位置与t时刻所处的位置相关，算法流程如图3所示，当收到人员落水的警报，首先输入落水人员报警位置、时间和预测时间，然后根据所需搜寻人员受的风压特性生成搜寻对象的初始位置样本，通过更新环境数据、计算漂移距离、更新漂移位置，与预测时间进行比对，如果达到预测时间则输出最终漂移位置，本次漂移轨迹预测结束；如果未达到预测时间需重新计算，直至达到预测时间为止。

5.2 实例分析

本实验利用Matlab软件仿真，采用的基础实验数据是我国渤海海域救生演练中通过给假人安装救生定位装置而获取的，将此实验数据作为实际数据。将实验数据的落水初始时间设置为0，初始位置误差为0，以初始位置圆心，以100m为半径，根据蒙特卡罗预测法预测落水人员的漂移轨迹得到本次漂移曲线，与目标的实际漂移曲线相比较。实验结果如图4所示。

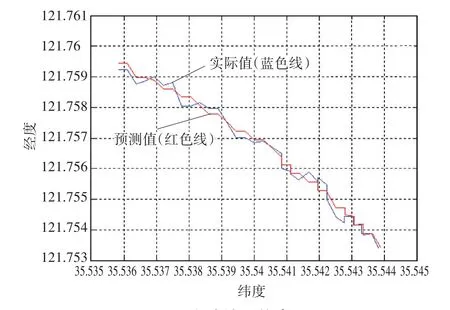
图4 实验结果仿真图

图中蓝色线表示为实际值，红色线为本实验预测值，实验证明当风速和流速较稳定时，通过蒙特卡罗法及分段插值算法得到的仿真曲线与实际曲线接近，能够预测目标的漂移轨迹。但对于海上落水人员而言，身体大部分处于海面下，而海况分析又较为复杂，导致流速对落水人员的漂移影响大，所以流场数据的精确度直接影响模型的实验误差。为此，利用分段线性插值算法对流场数据进行处理，提升其在时间上的精确度，流场数据进行线性插值后的误差均有所减小。