基于Lazy Theta*算法的反潜巡逻飞机航路规划研究∗
2021-01-19
(海军指挥学院 南京 210016)
1 引言
反潜巡逻飞机是现在乃至将来海上反潜作战的主要作战力量,由于其相对水面舰艇和潜艇反潜而言,机动性更强、搜索效率更高、不易被潜艇攻击等特点,得到各国海军的重视[1]。一般情况下,反潜巡逻飞机通常是在获得相关情报信息后,对指定海域执行巡逻反潜任务,或者对疑似潜艇目标执行应召反潜任务。
在规划反潜巡逻飞机飞行航路时,不仅需要考虑雷暴、云层等自然因素,还需要考虑蓝方防空火力、侦察探测的覆盖范围等战场态势。快速地为反潜巡逻飞机拟定安全、可靠、高效的飞行航线,是提高反潜巡逻飞机作战效率的有效途径之一。
目前,经典的航路规划方法主要有A*算法[2]、遗传算法[3~4]、蚁群算法[5~7]等。针对经典航路规划方法容易导致最终得到的路径不平滑、存在过多转折点的问题,本文采用Lazy Theta*算法,在搜索路径的同时允许以任意角度改变路径的方向、对路径进行平滑处理。经过仿真实验表明,能够得到平滑且距离更短的路径。
2 Lazy Theta*算法
Lazy Theta*算法通过进行启发式路径搜索,同时对父节点进行可达性检测分析,通过减少转向次数和缩短路径长度等方式,实现对搜索路径的高效优化[8]。其原理如图1所示。
其中,灰色区域表示障碍区域,白色区域表示自由区域。算法从起点作为扩展节点开始搜索,如图1(a),细箭头表示箭头所在点向起点进行可达性搜索;找到离终点最近的点后,以该点作为新的扩展节点进行可达性搜索,如图1(b);形成可能的路径并将途径障碍区域的路径调整为从自由区域经过,如图1(c)、图1(d),粗箭头表示可能的路径;以此类推,直到形成从起点到终点并避开障碍区域的路径 A4→B3→B2→C1,如图 1(e);但此时形成的并不是最短路径,该路径的基础上,通过判断各节点之间的通视性,对路径进行优化,得到最优路径A4→B3→C1,如图 1(f)。
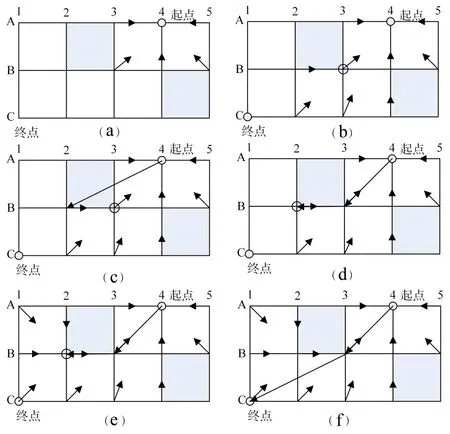
图1 Lazy Theta*航路规划算法步骤示意图
3 反潜巡逻飞机航路规划问题建模
3.1 几点说明
1)威胁区域包括该区域海平面以上的空域
在实际运用中,对于威胁区域往往是一个立体的概念,反潜巡逻飞机在规划航路时需要避开。安全起见,通常认为威胁区域覆盖了该区域从海平面到反潜巡逻飞机最大飞行高度的空间,反潜巡逻飞机一般不会采取调整高度的方式来规避某些防空火力的威胁,而是采用从区域外完全规避的方式飞行。基于此,可以将三维空间的航路规划问题简化为二维平面中的航路规划问题进行求解,大大提高计算效率,同时也保证实际运用的飞行安全问题。
2)区域内经线相互平行
在地理坐标系中,各经线之间并不平行,但反潜巡逻飞机飞行航路多集中于某一局部区域。由于区域跨度有限,在栅格化处理时可以近似的认为该区域内经线互相平行,这种处理对反潜巡逻飞机飞行航路规划的影响较小,同时也能简化计算、提高效率。
3.2 问题描述
反潜巡逻飞机航路规划问题实质上属于最优化问题的一种。其中,反潜巡逻飞机面临的战场环境即为最优化问题的约束条件,飞行航路的评价指标即为最优化问题的优化指标,最终规划的飞行航路即为最优化问题在满足约束条件下的全局最优解。
根据约束条件、优化指标的不同,反潜巡逻飞机航路规划问题可以分为不同的类型。
1)最短航路规划问题:将反潜巡逻飞机飞行路程作为优化指标的飞行航路规划。
2)最佳油耗规划问题:将反潜巡逻飞机飞行油耗作为优化指标的飞行航路规划,这种规划问题中通常还需要同时规划飞机在不同航路段的飞行高度和速度。
3)最安全航路规划问题:将反潜巡逻飞机飞行安全作为优化指标的飞行航路规划。
本文研究最短航路规划问题,考虑气象条件和蓝方威胁两类战场环境作为约束条件,以反潜巡逻飞机飞行路程作为优化指标进行研究。
3.3 战场环境建模
为便于把战场环境转化为数学化的约束条件,采用栅格法对反潜巡逻飞机面临的战场环境进行建模。将战场环境空间划分成多个同样大小的区域,对气象威胁和蓝方威胁转换成区域的可通过性进行描述。
通常情况下,反潜巡逻飞机飞行航路上的威胁区域在地图上的平面投影由一个或多个多边形组成。在不同的规划任务中,根据规划路径的精度要求,可以按照不同的精度对地图进行栅格化,其栅格化规则如下。
1)每个栅格的威胁性设置为威胁栅格和安全栅格,威胁栅格用1描述,表示存在威胁,飞机不可通过;安全栅格用0描述,表示不存在威胁,飞机可安全通过。
2)威胁区域在栅格上的投影完全覆盖栅格,认为该栅格是威胁栅格。
3)威胁区域在栅格上的投影覆盖不满一个栅格,认为该栅格是威胁栅格。
4)没有威胁区域投影覆盖的栅格,认为是安全栅格。
5)只对反潜巡逻飞机可能涉及的区域进行栅格化,为使问题简化,认为区域栅格的横轴与纬线平行,纵轴与经线平行,横纵轴相互垂直。
通过对地图进行栅格化,能够直观地描述反潜巡逻飞机的航路规划空间。栅格越小,对航路规划的计算也就越精细,但对应的计算量也显著增加,所耗费的计算时间也越多。在考虑航路规划精度的同时,需要考虑算法所耗费的资源和时间,避免过于繁冗的计算过程。
3.4 航路规划指标建模
在规划反潜飞机飞行航路时,需要建立各航路的性能优化指标。在地图栅格化的基础上,以栅格的横轴方向为x轴,纵轴方向为y轴,栅格的坐标以(x,y)表示,栅格的安全性函数f(x,y)可以表示为
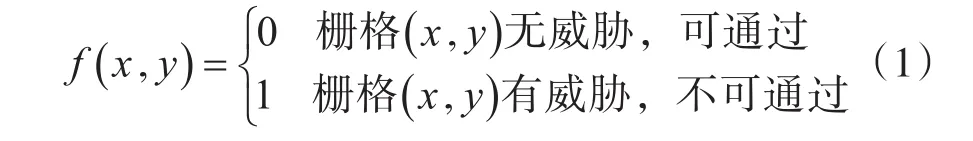
假设所有气象威胁的栅格集合为RW,所有蓝方威胁的栅格集合为RE,对于航路栅格集合R上的任意一个航路点栅格(xi,yi),应该满足f(xi,yi)=0,则航路规划问题的约束条件可以描述为
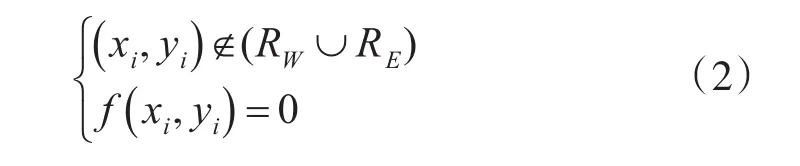
在避开气象威胁和蓝方威胁的基础上,以反潜巡逻飞机最短飞行航路作为优化目标,使飞机的飞行距离最小,对R上的任意一个航路点栅格(xi,yi),建立航路规划目标函数如下:
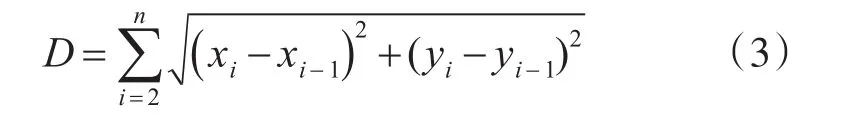
其中,n为航路点个数。满足使D最小的航路点栅格(xi,yi)集合和n即为满足安全条件下的最短航路和航路点的个数。
4 程序实现
4.1 地图栅格化
地图栅格化的程序计算流程如下。


其中,涉及两点间球面距离、点与区域相对位置的算法[9~10]已十分成熟,此处不再赘述。
4.2 基于Lazy Theta*算法的航路规划
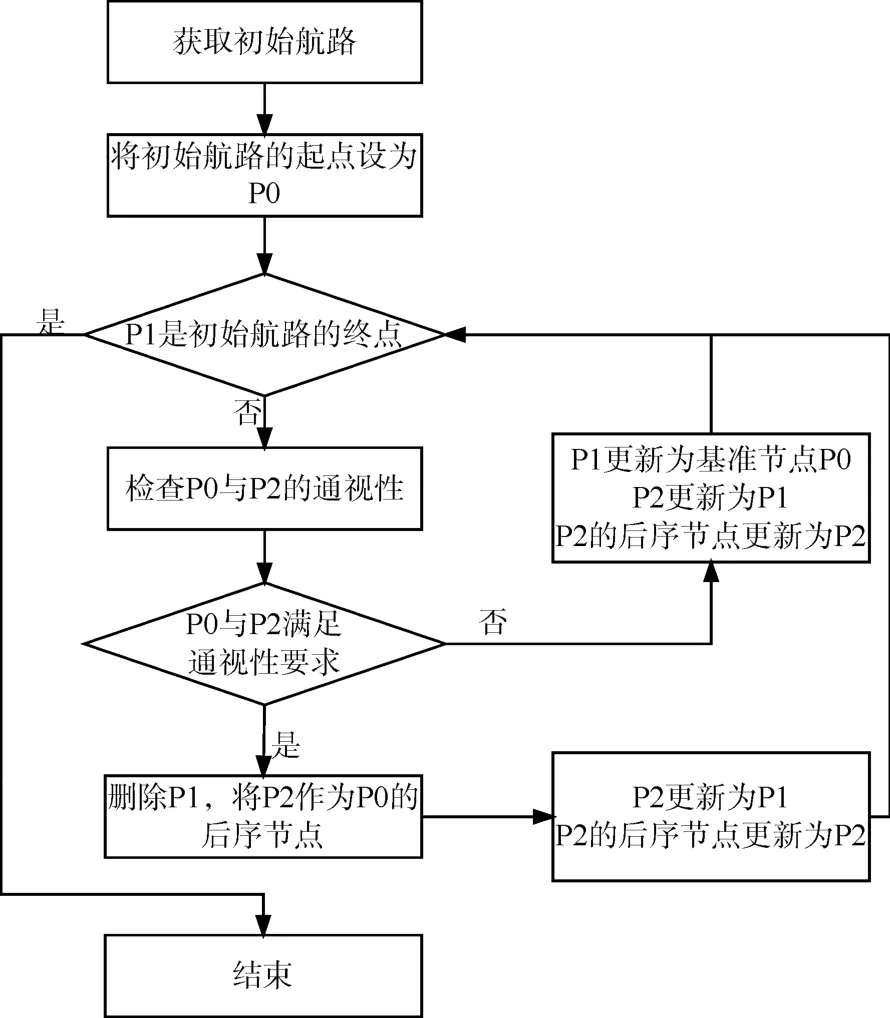
图2 Lazy Theta*算法平滑处理流程图
Lazy Theta*算法是Theta*算法的改进,其核心在于运用Theta*算法求得航路后,对所得航路进行平滑处理,从而进一步缩短航路的距离、减少航路转弯次数[11]。其平滑处理的程序计算流程如下,该流程中,优化的基准点记为P0,P0的后序节点记为P1,P1的后序节点记为P2。
在规划航路的过程中,如何保留最有价值的节点作为航路的一部分有多种判断方式。结合最短航路规划的目标,主要以该节点与终点之间的距离、该节点和终点的连线与起点和终点连线形成夹角的大小作为判断依据,距离越短价值越高,距离相同的情况下,夹角越小价值越高。
4.3 实例化
将本文提出的反潜巡逻飞机航路规划思路进行计算机实现,形成反潜巡逻飞机航路规划辅助决策系统。系统能够根据飞机的起飞机场、执行反潜任务的目标海区以及需要避开的危险区域,采用Lazy Theta*算法自动生成飞机从机场至目标海区的飞行航路。
假设当前时刻,某海域发现不明潜艇信号,获取到其可能的航向航速信息,位于A机场的反潜巡逻飞机起飞赴不明信号所在海区执行应召反潜任务,为保障任务的隐蔽性和安全性,飞机需避开蓝方驱逐舰的对空雷达探测范围和禁飞区。根据不明潜艇可能的航向航速信息和信号所在海域与A机场的直线距离,可以初步判断飞机飞抵海区时其反潜目标海区为不明潜艇前方扇形区域[12],系统初始态势如图3所示。
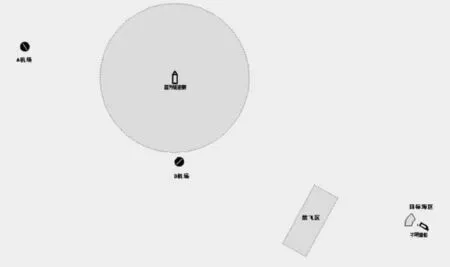
图3 初始态势示意图
基于初始态势,系统对相关区域进行栅格化操作,如图4所示,以平行纬线方向为X轴,平行经线方向为Y轴建立栅格坐标系,使地图上的每一个点都能对应到某一个栅格当中。
在初始态势栅格化的基础上,采用Lazy Theta*算法计算的飞行航路如图5所示。最后将栅格坐标还原为经纬度坐标即为计算结果,如图6。需要说明的是,图4和图5所示的过程为计算机后台计算和处理的示例,并不会呈现在指挥人员和决策者面前。若指挥人员和决策者对航路规划结果不满意,可以通过系统对威胁区域进行增删改,再自动规划相应的航路,也可以直接在已有航路规划结果的基础上增加、删除航路点或对航路点的坐标进行修改,直至获得满意的结果。
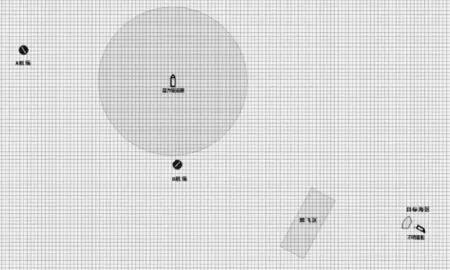
图4 初始态势栅格化
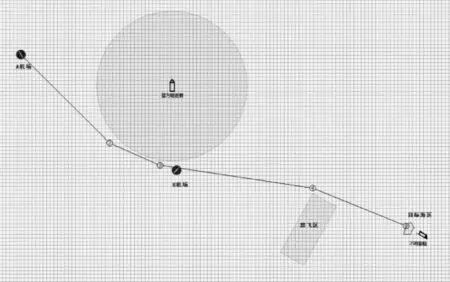
图5 栅格状态下的航路规划结果
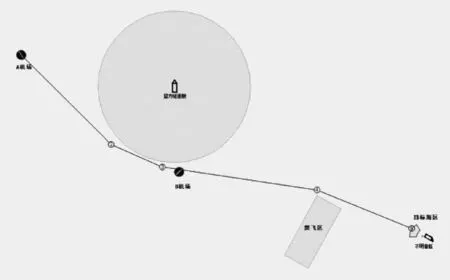
图6 航路规划计算结果
从图6所示的结果来看,算法自动规划的飞行航路能够避开预先设定的威胁区域,且保持航路距离最小,作为以飞行路程作为优化指标的航路规划问题,其规划结果能较好地满足要求。
5 结语
本文针对反潜巡逻飞机飞行航路规划问题,建立了战场环境和航路规划指标模型,将Lazy Theta*算法运用于模型求解过程;设计了地图栅格化和Lazy Theta*算法解决该问题的计算机程序逻辑,采用C++语言对这些过程进行了计算机实现;通过应用实例,验证了航路规划模型的正确性和Lazy Theta*算法在解决该问题过程中的有效性,能够为指挥人员和决策者提供一定的决策支撑。
