基于灰关联分析与证据理论的目标识别方法∗

（海军航空大学 烟台 264001）

1 引言

辐射源识别是电子侦察的重要内容，它决定了电子侦察系统的性能优劣，是形成电子情报的基础。辐射源识别就是将侦测得到的辐射源参数与数据库中的辐射源特征参数进行比对，从而推导出辐射源型号的过程。在此基础上，还可以进一步分析，得到相关武器系统的工作状态、活动规律以及战术运用特点，实现对威胁等级的判断，对战场态势的判读。

对于辐射源识别的研究由来已久，现在常用的主要有特征参数匹配法［1］、基于专家系统的识别方法［2］、基于神经网络的识别方法［3］、脉内特征分析方法［4］、基于模糊推理的识别方法［5］等。目前，灰色关联理论也被人们更多地应用于辐射源识别领域。文献［6］讨论了灰关联理论应用于辐射源识别的可行性。文献［7］研究了基于D-S推理的灰关联识别算法，提高了正确识别率。但是以往用于辐射源识别的大多是邓氏关联度，对于其他形式的灰关联度没有进行深入的研究。不同的灰关联度都是从不同的角度来刻画两个向量之间的相似程度。本文先研究了几种不同形式的灰关联度单独应用于目标识别时的效果，然后由以识别效果较好的灰关联度为基础，得到基本概率赋值函数。最后通过证据理论将由不同形式灰关联度得到的基本概率赋值进行组合，并根据组合后的基本概率赋值进行决策。

2 基于灰关联分析的辐射源识别方法

灰关联分析就是利用灰色关联模型来衡量变量之间的相互关系［8］。其基本原理是通过研究系统序列曲线的几何接近程度来体现序列之间关系的密切程度，即曲线的形状越相似，它们之间的关联度就越大。

2.1 模型的建立

进行灰关联分析先要确定参考序列与比较序列，选取侦察设备上报的待识别目标向量为参考序列，选取雷达数据库中的雷达特征向量为比较序列。雷达的特征向量通常由载频（RF）、脉宽（PW）、重频（PRF）等特征参数表示。在仿真时，我们依据一定的规则赋给每个特征向量合适的参数。

2.2 灰关联分析的基本流程

灰关联分析一般分为数据标准化、灰关联度计算、基于灰关联度进行决策这几个关键步骤。

2.2.1 数据标准化

出于提高建模精度的考虑，灰色系统理论在建立模型之前要对原始数据进行一些处理，以便消除数据的量纲不统一情况和不可比性。本文采用区间化生成的方法来对数据进行标准化。公式如下:

其中j=1,2,…,k，i∈R。

2.2.2 灰关联度

灰关联度是用来评价事物之间、因素之间关联性大小的指标。现有计算灰关联度的形式有很多，本文使用的是邓氏关联度、绝对关联度、相对关联度与斜率关联度。

记侦察设备侦测到的信号X0={x0(1),x0(2),…,x0(n)}为参考序列，以雷达数据库中的雷达特征向量Xi={xi(1),xi(2),…,xi(n)}为比较序列。

对于邓氏关联度来说，第一步是先计算邓氏关联系数，即

绝对关联度研究的是两组数据增量绝对值间的关系，其物理含义是两条曲线间所夹的面积大小。对于绝对关联度来说，在计算之前需先得到各条序列的始点零化象。记X0与Xi的始点零化象为，则X0与Xi之间的绝对关联度的为

公式内每一个符号的含义都与绝对关联度计算公式内的对应符号相一致。

2.2.3 基于灰关联度的决策

灰关联度分析是根据事物或因素间曲线的相似程度来判断其关联程度的。因此，我们采用最大关联度识别原则。

3 基于灰关联分析与证据理论的融合识别方法

证据理论是由Dempster于1967年提出的，后来由Shafer发展，所以证据理论又称D-S理论［9］。证据理论可以处理由不知道所引起的不确定性。它采用信任函数而不是概率作为度量。它通过对事件概率的约束来建立信任函数，而不要求得到精确的概率。

基本概率赋值是证据理论研究的重要概念，本文将以灰关联度为基础构造基本概率赋值。设U为一识别框架，则函数m:2U→[0 , 1]（2U为U的所有子集）在满足下列条件:

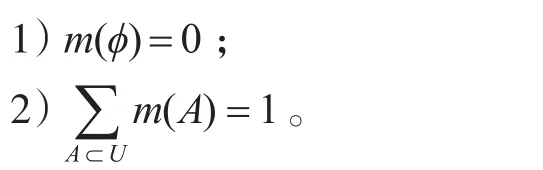
时，称m(A)为A的基本概率赋值。m(A)表示对命题A的精确信任程度，表示了对A的直接支持。

3.1 基于多种灰关联度的融合识别算法步骤

在灰关联分析的基础上，应用证据理论进行融合，提高正确识别率。具体过程是:

1）计算待识别信号与雷达数据库中各个特征向量之间的灰关联度。计算完所有关联度后，将其存于关联度矩阵。

2）对灰关联度进行归一化，构造基本概率赋值。记某条证据的基本概率赋值为m(i)，则

3）将由不同形式灰关联度得到的基本概率赋值根据组合规则进行融合，得到新的基本概率赋值并进行决策。

3.2 证据理论融合规则

设U表示X所有可能取值的一个论域集合，且所有在U内的元素是互不相容的，则称U为X的识别框架。设m1,…,mn是2U上的n个相互独立的基本概率赋值（Basic Probability Assignment，BPA），现在我们想要得到组合后的基本概率赋值:m=m1⊕…⊕mn。

式中，若K1≠1，则m为合成后的基本概率赋值。若K1=1，则认为m1,…,mn矛盾，没有联合概率赋值。K1的大小反映了证据的冲突程度。由上式给出的组合规则称为Dempster组合规则。

3.3 基于绝对值距离确定权重的冲突合成法证据

由于经典的Dempster组合规则不适合处理证据出现高冲突的情况［10］，众多的研究人员提出了改进方法。Murphy［11］提出了先将基本概率赋值进行平均，在进行证据合成的方法。王肖霞［12］提出了一种利用证据间相似系数确定权重，将BPA加权平均再进行合成的方法。采用相似的思路，本文提出了一种基于绝对值距离确定权重的冲突合成法，其思路是计算证据间绝对值距离及可信度并确定权重，再将证据的基本概率赋值进行加权平均并合成。

对于证据E1与E2，它们的基本概率赋值分别为m1，m2，则两条证据之间的绝对值距离为

其中m1(i)、m2(i)分别是m1、m2内各个焦元的基本概率赋值。两个矢量越相似，它们之间的绝对值距离越小。

计算所有证据间的绝对值距离，得到绝对值距离矩阵:

将绝对值距离矩阵的每一行相加，则可以得到该证据与其他证据绝对值距离之和:

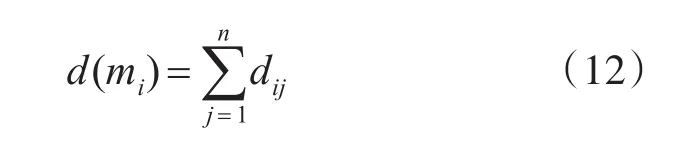
因为距离之和越小，表示其他证据对它越支持。令证据Ei的支持度为

可信度计算公式为

根据证据的可信度确定权重，计算BPA的加权平均，再进行合成。其基本流程如下:

1）计算证据间的绝对值距离，得到距离矩阵。

2）计算证据的支持度和可信度。

3）确定权重，对BPA加权求和。

4）用Dempster组合规则进行证据的合成。

4 仿真分析

4.1 不同灰关联度应用于辐射源识别的优劣

在本文的仿真中，我们假设存在20个雷达类，每个雷达类都可能存在多个工作模式。按均匀分布随即抽取100个雷达射频数据，100个雷达脉冲重频数据，100个雷达脉宽数据，100个天线扫描周期数据，组合成100个工作模式，并且把这100个工作模式等概率随机分配给20个雷达类，每类的工作模式数目都是随机的。在抽取参数时，限定信号载频的范围为2GHz～10GHz，脉冲重复频率为200Hz～300KHz，脉宽为0.1μs～80μs，天线扫描周期为0.1s～100s。

在模拟待识别信号时，我们抽取某一类雷达的某种工作模式，并叠加上一定的随机误差，来模拟电子侦察系统接收到的信号。本文假定随机误差服从正态分布。

在进行不同灰关联度的仿真时，我们分别进行1000次独立的仿真，并根据仿真结果计算出正确识别率。本文通过Matlab来进行建模仿真，研究采用不同关联度对识别效果的影响，还研究了不同噪声环境对正确识别率的影响。我们把噪声对信号参数的影响转化为待识别信号随机生成时方差大小。噪声环境越差时，生成的待识别信号方差越大。第一种情况的方差是原参数的2%。第二种情况的方差是原参数的5%。第三种情况的方差是原参数的10%。

表1 不同关联度应用于辐射源识别的正确识别率

从仿真结果，我们可以发现以下结论:

1）正确识别率与测量误差的关系。通过对不同测量误差情况下的仿真，我们发现当测量误差较小的时候，识别效果比较好；当测量误差增大时，正确识别率随之降低。

2）不同灰关联度应用于辐射源识别的优劣。邓氏关联度与斜率关联度用于辐射源识别的效果较好，而绝对关联度与相对关联度用于识别的正确率低下。本文进行灰关联分析时的序列，仅有四个参数方向，数据序列的维度较小。而绝对关联度和相对关联度的计算都与始点有着密切的关系，其进行的处理使得始点x(1)不是0就是1，相当于第一维信息丢失了，使得有效信息变得更小，导致了正确识别率低下。

4.2 基于灰关联分析与Dempster组合规则的融合识别方法

在仿真中，由相对关联度和绝对关联度来进行识别的方法正确率太低。因此，在的仿真中，我们仅以邓氏关联度与斜率关联度为基础，得到基本概率赋值函数。在融合时，还通过控制证据数n来研究融合时证据数对正确识别率的影响。进行完证据的组合后，得到新的基本概率赋值函数并进行决策，判断待识别目标向量来自于数据库中雷达类的哪个工作模式。

表2 融合后的正确识别率

从仿真结果中，我们能发现:

1）与单纯使用灰关联分析方法进行辐射源识别相比，采用该方法能提高正确识别率，在环境噪声越大、识别率较低的情况下，提升效果更加明显。同时，当证据数较小时，增加融合的证据数可以提高正确识别率。

2）测量误差对正确识别率有较大的影响。随着测量误差的增大，正确识别率会降低。

4.3 基于绝对值距离确定权重的冲突合成法

表3 采用新方法进行融合后的正确识别率

由仿真得到的数据，我们发现在进行融合时采用基于绝对值距离确定权重的冲突合成法可以减小证据之间的不一致或冲突带来的影响，有效提高正确识别率。特别是当噪声环境比较恶劣时，对识别效果的改善作用更加明显。

5 结语

本文对基于灰关联分析的辐射源识别方法进行了研究，比较了邓氏关联度、绝度关联度、相对关联度以及斜率关联度应用于辐射源识别的效果。通过仿真，我们发现邓氏关联度、斜率关联度用于辐射源识别的效果较好，而绝对关联度与相对关联度的正确识别率低下，不适用于辐射源识别。同时，本文以识别效果较好的邓氏关联度与斜率关联度为基础，构造了传感器的基本概率赋值，由证据理论融合规则得到了最终的基本概率赋值并进行判决。最后本文还提出了一种基于证据间绝对值距离确定权重的冲突合成方法。该方法先计算两两证据之间对应位置基本概率赋值之差的绝对值之和，构造绝对值矩阵并计算支持度与可信度，并根据可信度对证据的基本概率赋值进行加权平均，再进行融合。通过仿真，证明了该方法在辐射源识别中的有效性和可行性。