基于宽度学习的结构沉降预测
2021-01-19陈永红甘文娟
陈永红,甘文娟,孟 雪,韩 静
(长安大学 信息工程学院,陕西 西安 710064)
0 引 言
随着现代化的飞速发展,结构工程建设的脚步不断加快。工程建设进程中结构受多种主客观因素影响而不可避免发生形变,严重形变量所引发的重大灾害给人民生命和财产安全带来了巨大损失。因此,对结构工程的施工和运营阶段提出了更严格的安全性要求,并且对结构变形进行自动监测也至关重要。采用科学完备的预测模型对结构沉降监测数据进行预测,可以指导有关部门及时采取有效的预防措施,提高工程建设的效率,保障施工建设的安全。当前,为了对结构沉降进行客观准确实时的预测,预测精度和训练速度已成为结构沉降变形预测关注的重点。
常用的结构变形预测模型主要有回归分析预测模型、灰色理论预测模型、时间序列分析预测模型和人工智能预测模型等。回归分析预测模型通过分析大量变形数据与影响变形因素之间的数学关系,建立回归方程进行模型预测[1]。其要求进行分析的数据具有较好的分布规律。该预测模型的精度由影响结构变形的因素决定。为达到简化预测模型的目的,通常采用线性回归模型进行结构变形预测,而实际的变形监测变量之间都是相互关联的,因此该模型在结构沉降预测方面具有一定的局限性。灰色系统理论最早由邓聚龙教授提出[2],用于研究小样本数据、贫信息等问题。灰色系统理论的重要部分是灰色预测,其中GM(1,1)是广
泛应用的预测模型[3]。灰色预测模型对数据的波动变化不敏感,而对数据的光滑度要求较高。灰色分析要求数据包含完整变化趋势,防止当数据序列较大且快速变化时模型预测误差增大预测精度降低而导致模型预测失效。以上问题限制了灰色系统理论在实际预测中的应用。时间序列法是一种数理统计学的动态数据处理法。AR自回归模型、MA移动平均模型、ARMA自回归移动平均模型[4-5]、ARIMA自回归求和移动平均模型[6]都是应用广泛的时间序列分析模型。时间序列的研究依赖于数据随时间变化的规律,其最突出的优点是可以找到历史数据在时间变化范围内的规律,实现对未来数据的预测。时间序列的预测结合了影响结构沉降的外部因素,但由于预测中的参数不能实现动态变化,使模型对于快速变化的数据预测精度较差。时间序列模型进行预测的前提是数据满足线性关系,而实际的结构变形数据是含趋势项和随机部分的非线性数据。因此时间序列法应用于结构沉降预测的发展不是很理想。
近些年,随着人工智能的蓬勃发展及大数据时代的出现使得应用人工智能预测方法解决结构变形预测问题成为热点。目前神经网络法[7]、支持向量机[8]等都是应用广泛的人工智能预测[7-12]方法。神经网络模型对非线性数据、非确定性系统具有良好的描述特性和抗干扰能力,是一种有效的结构沉降预测算法。但是该模型参数设置缺乏理论支撑,易出现收敛速度慢、局部最优等问题。支持向量机预测模型对于小样本、非线性和局部极小点等问题具有良好的解决能力,但对于突变数据的处理存在预测失效的可能。最初针对神经网络预测模型的研究大部分采用浅层结构,然而随着人们对结构沉降预测精度要求的不断提高,浅层神经网络的预测精度已不能满足实际需求,深度学习被提出。近些年来,随着机器学习研究热潮的出现,深度学习逐渐应用于结构沉降变形预测。深度学习网络结构的实质是多层神经网络,其学习能力和模型泛化性均良好,适合处理大规模数据。目前应用深度学习的结构沉降预测模型[13-15]已非常强大,但是仍然存在一些亟待解决的问题。为解决深度学习网络模型结构复杂、训练耗时等问题,宽度学习系统应运而生。宽度学习的提出旨在为深度学习提供一种替代方法。宽度学习是一种新的机器学习算法,和深度学习算法相比,具有模型结构简单、训练速度快、实时性高的优势。宽度学习系统通过对监测数据进行训练,构建预测模型,实现对结构沉降监测数据的预测。与现有预测模型相比,宽度学习预测算法具有更快的训练速度和更高的预测精度。
1 宽度学习系统的结构沉降预测方法
1.1 宽度学习系统模型
宽度学习系统(board learning system,BLS)[16]是基于随机向量函数链接神经网络(random vector functional-link neural network,RVFLNN)[17-18]提出的一种新的学习算法。RVFLNN是一种浅层神经网络,基本思想是初始数据和其经过简单映射后的结果共同构成模型输入训练得到输出。宽度学习系统结构如图1所示。该模型的本质是一个单层网络,其通常由输入层、隐藏层和输出层组成,隐藏层由映射特征节点层和增强节点层构成。首先,初始数据经过线性特征映射函数连接输入权值矩阵变换得到映射特征组,输入权值通过稀疏自编码器产生。然后映射特征组经过线性映射和非线性激活函数连接权值矩阵得到增强节点。最后增强节点和映射特征节点共同连接输出权值矩阵得到系统输出,输出层权重通过岭回归近似广义逆计算得到。
(1)映射特征组。
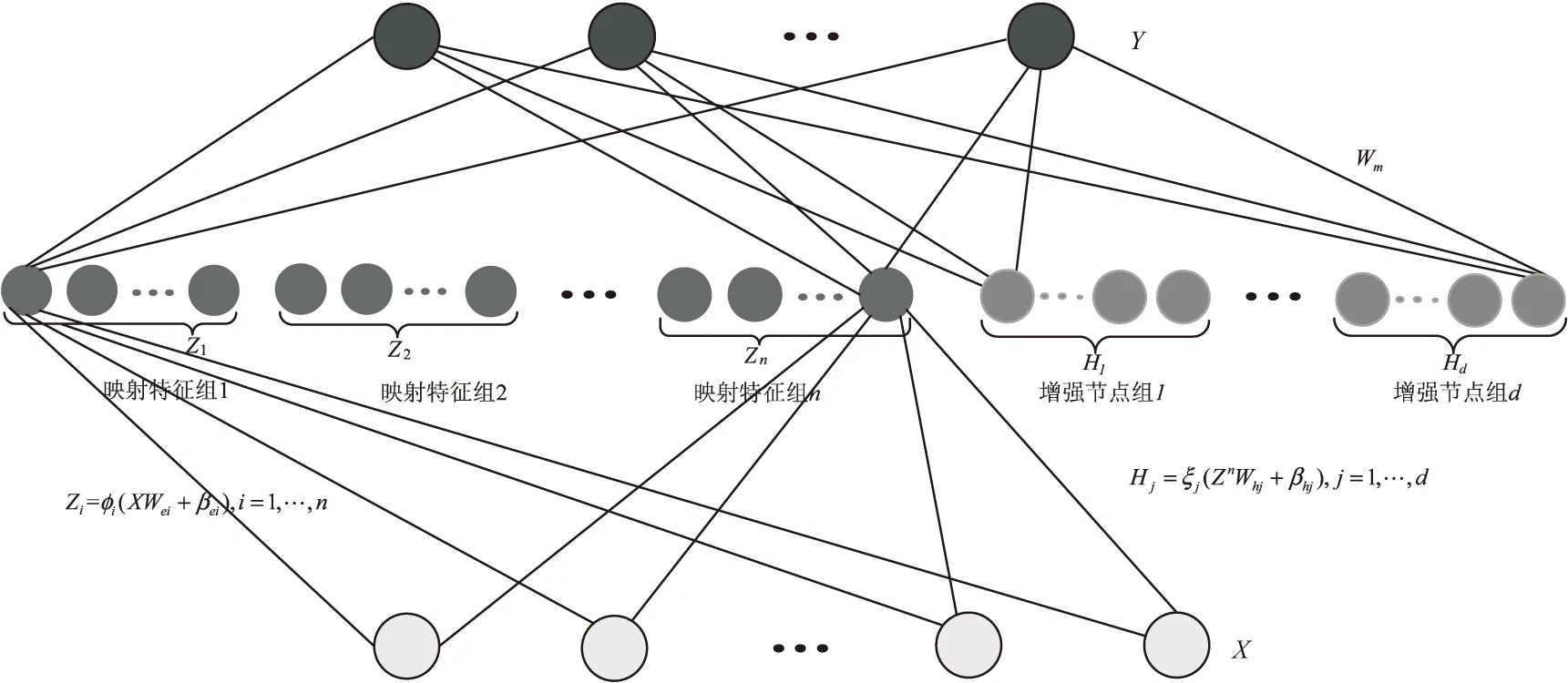
图1 典型宽度学习系统结构示意图
X∈Ra×b表示模型训练的输入数据,其数量为a,维数为b,Y∈Ra×c表示模型训练输出a个c维的数据,φi(·)表示特征映射函数,第i组特征映射用Zi表示,所有的特征映射组用Zn表示。
(1)
其中,Wei表示第i组由稀疏自编码得到的最优输入连接权值矩阵,βei表示从输入层到映射特征节点层的与Wei相对应的偏置矩阵。权重Wei的维数决定了映射特征组Zi中的节点数。
(2)增强节点组。
增强节点组由映射特征组经过函数映射变换得到,第j组增强节点组用Hj表示,所有的增强节点组用Hd表示:
(2)
其中,ξj表示非线性激活函数,Whj表示第j组映射特征节点到增强节点层的随机连接权值矩阵,βhj表示第j组偏置矩阵,增强特征组的个数为d。
(3)结果输出。
增强特征节点和映射特征节点共同作为系统输入,则宽度学习系统的输出为Y:
Y=[Zn|Hd]Wm=
[Z1,Z2,…,Zn|H1,H2,…,Hd]Wm
(3)
其中,[Zn|Hd]矩阵表示BLS模型的实际输入,Y作为系统输出在文中表示结构沉降预测值,Wm是连接系统输入到输出层的权值矩阵,通过求解岭回归矩阵伪逆的方式得到。
BLS的输出用式(3)表示,该问题的求解通过采用岭回归近似广义逆[Zn|Hd]+得到,计算公式如下:
Wm=(λI+ATA)-1AΤY
(4)
其中,A=[Zn|Hd],I表示单位矩阵,λ表示正则化系数。
1.2 BLS结构变形预测模型
图2是BLS结构变形预测算法流程。对地铁沉降数据进行预处理,将进行归一化处理的数据划分为训练集和测试集用于BLS网络的训练和测试。BLS网络进行学习的全过程:输入样本P产生包含特征映射节点的映射特征组,映射特征组连接非线性激活函数产生增强节点组,映射特征组和增强节点组共同作用到输出层得到BLS模型的输出U。BLS模型的输出数据,需先进行反归一化得到最终的地铁沉降预测数据。将原始地铁沉降数据和预测数据比较,采用误差值判断BLS模型对结构沉降数据的预测精度,采用测试时间验证BLS模型训练速度的优越性。进一步对不同预测模型的结果进行比较,画出不同模型预测形变量与真实形变量对比图。
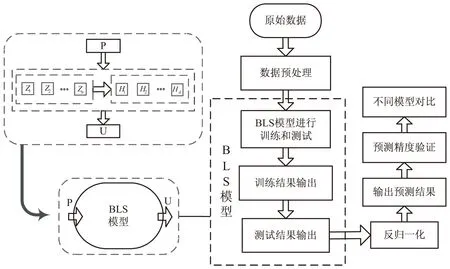
图2 BLS结构变形预测算法流程
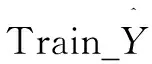

(5)
(6)
Train_Y=Φ(Train_X)
(7)
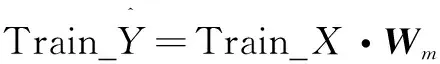
(8)
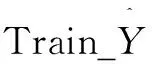

(9)
(10)
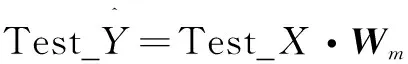
(11)

2 实 验
2.1 数据集介绍
实验数据来源于某地铁5号线的地下隧道沉降数据,该数据集包含131个数据,监测时间段是从2016年03月10日到2016年12月29日。宽度学习系统本质是一种机器学习算法,由于原始131个地铁监测数据样本量较少,为了验证模型的有效性,实验采用三次样条插值法对监测数据点进行10倍插值。将插值后的数据按顺序以7∶3的比例划分为训练集和测试集,并对数据集进行归一化处理。对数据进行归一化可降低数据之间存在的差异性,在一定程度上减少训练时间,提高测试精度。实验采用最值归一化(min-max normalization,MMN),其实质是对数据进行线性变换,使数据结果值定义到[0,1]区间。模型对归一化数据进行预测,因此需要对预测结果进行反归一化。反归一化公式由归一化公式转换得到。归一化和反归一化公式如下:
(12)
y'=y·(xmax-xmin)+xmin
(13)
其中,x表示原始数据,x'表示原始数据归一化后的数据,xmin表示原始数据的最小值,xmax表示原始数据的最大值,y表示预测数据,y'表示对预测数据进行反归一化的值。
2.2 模型评价指标
该文采用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)作为评价模型预测精度的指标。这两种误差的公式如下:
(14)
(15)

RMSE的计算可以得到预测值与真实值之间的偏差。MAPE的计算可以得到绝对误差与真实值之间的比例。RMSE、MAPE是常用的模型预测精度的评价指标。RMSE、MAPE值的大小,表示预测精度的高低。值越小,预测精度越高。
2.3 实验结果及分析
经过多次实验,当映射特征组数、映射特征组内节点数和增强特征节点数分别取12、12、15,正则项参数C为2-20时,宽度学习模型对地铁沉降监测数据的预测结果最好。模型预测值与原始地铁沉降值对比结果如图3所示。此时,模型测试集均方根误差为0.006 3,平均绝对百分比误差为0.000 4,测试时间为0.069 3 s。
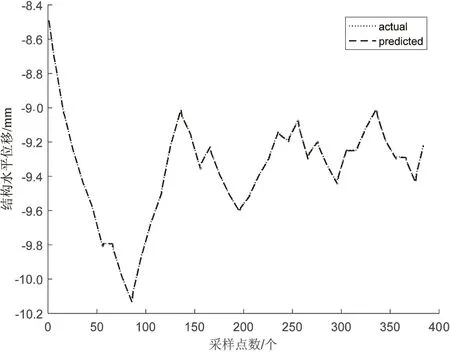
图3 BLS预测结果
为了验证BLS模型在结构沉降预测方面的有效性,实验将BLS模型与深度置信网络-支持向量回归(deep belief networks,support vector regression,DBN-SVR)、支持向量回归(support vector regression,SVR)和人工神经网络(artificial neural network,ANN)模型对地铁沉降监测数据的预测结果进行比较。四种不同模型预测性能评价如表1所示。模型预测结果采用均方根误差(RMSE)、平均绝对百分比误差(MAPE)和运行时间进行评估。
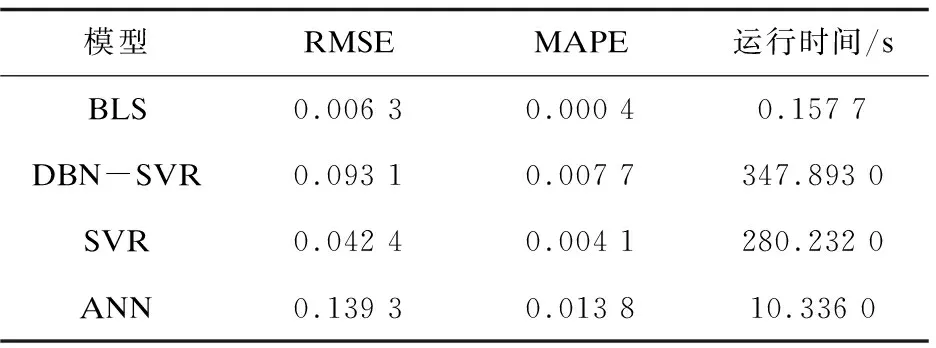
表1 四种模型性能评价
由表1可知,BLS模型预测误差最小,运行时间最快。BLS模型预测精度达到了99.96%,运行速度最快仅为0.157 7 s(训练时间为0.088 4 s,测试时间为0.069 3 s)。对四种预测模型的性能进行评价可知,BLS模型的预测均方根误差(RMSE)和平均绝对百分比误差(MAPE)明显小于其他三种对比模型。BLS的预测精度比DBN-SVR、SVR和ANN分别提高了94.81%,90.24%,97.10%。BLS模型的运行速度相比于对比模型提高了数十倍至数千倍。综合考虑模型的预测精度和运行速度,BLS模型用于地铁沉降数据预测,具有非常高的预测精度和非常快的运行速度。
通过上述DBN-SVR、SVR、ANN和BLS预测模型的实验,得到BLS与DBN-SVR、SVR和ANN的预测值与真实地铁沉降值的曲线对比结果,如图4所示。

图4 不同模型预测结果
由图4可知,BLS对地铁沉降数据预测的拟合度非常高,即预测值与原始地铁沉降数据高度吻合;在沉降数据变化的拐点处也可以实现精确预测,即局部拟合度也非常高;ANN的拟合度最差,其预测结果和原始数据的变换趋势整体大致符合。
图5为BLS、DBN-SVR、SVR和ANN的预测误差对比,其直观分析了四种预测模型的预测误差。由图5可知,BLS预测误差最小,即预测精度最高。实验结果表明,BLS预测模型相比于其他预测模型具有更高的预测精度和更快的运行速度,是一种预测性能优良的结构沉降数据预测算法。
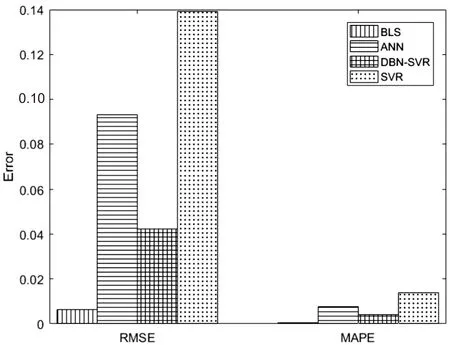
图5 不同模型误差对比
进一步在不改变模型其他参数的前提下,通过调整模型的正则项参数C,得到宽度学习系统对结构沉降数据的预测结果(见表2),验证其对模型预测精度的影响。由表2可知,正则项参数C设置为2-20时,模型预测效果最佳,即预测误差最小,但此时模型运行速率不是最快。

表2 正则项参数对BLS预测结果的影响

图6 正则项参数对模型预测准确率的影响
图6中预测准确率是通过1-MAPE定义的。图中随着正则项参数C的缓慢增加,宽度学习系统对于结构沉降预测准确率呈缓慢下降趋势,预测准确率从99.96%下降到99.24%。在一定范围内,改变正则项参数C对基于宽度学习系统的结构沉降预测准确率的影响非常小。
3 结束语
提出了一种基于宽度学习的结构沉降数据预测模型,通过实测地铁沉降数据测试结果表明,宽度学习系统模型的预测值和真实值基本吻合,即使在结构沉降数据变化的拐点处吻合度也较高。进一步将BLS与DBN-SVR、SVR和ANN模型预测结果进行对比,模型预测精度采用预测误差进行验证,模型预测速度采用模型运行时间进行评估。实验结果表明,提出的宽度学习系统模型预测精度高、运行速度快,是一种性能良好的结构沉降预测方法。宽度学习系统可通过引入增量学习算法,改变原系统的性能,在将来的研究中应进一步研究增量学习算法对宽度学习系统结构沉降预测精度的影响。
