基于VNF间性能干扰的服务请求调度策略
2021-01-19史久根谢熠君
郭 胜,史久根,孙 立,谢熠君
(合肥工业大学 计算机与信息学院,安徽 合肥 230601)
0 引 言
网络功能虚拟化(network function virtual,NFV)技术的特点在于实现硬件与软件的分离,通过网络功能的虚拟化,将虚拟网络功能(virtual network function,VNF)运行在通用硬件之上,不需要专用硬件,减少成本支出[1]。虚拟网络功能可以放置在虚拟机(virtual machine,VM)节点提供特定的网络功能[2]。通过VM迁移,VNF可以部署在网络中任意一个商用服务器中,同时这种新的模式也带来了一些挑战。首先,数据包需要经过一组VNF,即服务功能链[3](service function chain,SFC),网络运营商会考虑如何将VNF部署在候选服务器中以减少端到端延时。例如,Zhang等人[4]以最大化平均资源利用率和最小化请求平均响应延时为目标,提出了综合考虑VNF服务链放置及服务请求调度的问题。其次,要提高资源利用率,VNF布局根据流量变化动态调整VNF实例的数量。例如,Eramo等人[5]提出VNF迁移策略,使得网络运营商得知VNF最佳的迁移的时间和地点,以节约资源。最后,现有的VNF实例可能需要合并到另一台服务器以释放和关闭一些服务器来节省资源。现有研究致力于研究应对上述挑战并提供高效的VNF放置方法。例如,Li等人[6]考虑不同VNF,在同一时隙对硬件计算量的需求不同,故将时变负载相关度最小的VNF放置在同一节点,达到计算资源互补,并采用多租户策略共享VNF,从而减少物理机的使用量来减少资源消耗。
然而现有的VNF放置方法大都没有将VNF同位间的性能干扰问题考虑在内。虽然虚拟化技术在VM之间提供了一定程度的性能隔离[7],但VNF在一个共享的硬件基础设施上运行时仍存在明显的性能干扰[8]。当流量监视器与入侵检测系统同时运行时,流量监控器的吞吐量下降了38.47%[9]。但是,为了最大化资源利用率和降低功耗,网络运营商倾向于将VNF实例放在同一物理上的服务器尽可能多,导致资源匮乏竞争和严重的性能干扰。同时,在数据流增大的时候干扰也随之增强。由于数据流的增大,VNF处理任务增加,所需的资源也随之增加,导致基本硬件资源的竞争更加激烈。
针对上述问题,该文根据不同类型的虚拟网络功能的工作特性,通过在虚拟机中运行工作特性相似的应用以及文献[9]的分析,得出不同的虚拟网络功能对CPU、Memory、Cache等资源的依赖程度,设计一个CAPA算法解出VNF之间的最佳组合,使得整体干扰度最小,并进行放置。其次,根据不同VNF对数据流量的处理特性,使用TAA算法进行服务请求的调度,从而进一步减小虚拟网络功能的干扰程度。仿真结果表明,该方案缓解了VNF间的干扰,提升了网络吞吐量。
1 问题描述
该模型需要解决的问题是,根据不同虚拟网络功能间干扰程度不同,对每个VNF进行组合,要设法使其双方的干扰度都尽可能小,并对服务链请求进行合理的调度,使得整体网络中的虚拟网络功能受到的干扰最小。
1.1 同位间虚拟网络功能干扰
同位间虚拟网络功能干扰是指,同一个物理中VNF会产生一定的性能干扰,使得彼此间性能下降。由于VNF对各种硬件资源的需求不尽相同,若多个同种资源需求密集型VNF放置在同一服务节点,会引起服务节点底层的某一资源过度占用,从而使得服务节点整体处理性能下降。在图1中(a)表示当VNF1与VNF2独立运行在服务器时的处理能力,(b)表示新增的VNF3分别放置在先前的服务器中,使得三个VNF处理能力都有不同程度的下降。由于各VNF,对不同的资源需求的比重不尽相同,可以通过资源互补的形式进行合理组合。如图2所示,左边部分表示三种VNF对不同资源的需求(每个颜色的柱型代表一种资源),右上侧VNF1+VNF2表示VNF1与VNF2进行组合,右下侧VNF1+VNF3表示VNF1与VNF3匹配,故合理的组合可以达到较优的效果。

图1 VNF间性能干扰示例
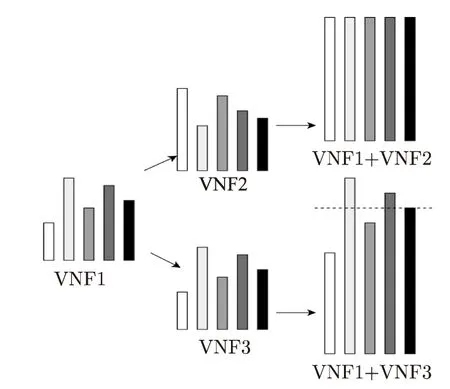
图2 VNF匹配方案示例
1.2 修改数据流的大小
VNF会对数据包进行分析,根据特殊的业务需求对数据包添加包头,或者对数据包进行优化压缩,使得数据包的字节数及数据流的大小都被改变[10]。目前VNF的总数很多,与路由器的数量相当[11],其中很大一部分的VNF有改变数据流大小的性质。如图3所示,网络功能F1可将数据流修改为原来的两倍,F2则将数据流修改为原来的一半,所以数据流先经过F2时,可减缓F1的处理负担,而VNF的流经顺序是部分可调的[12-13]。

图3 VNF修改数据流示例
数据流的减小和增大直接影响VNF工作时对资源的竞争程度。因此合理的调度方案可以进一步减小干扰。
2 系统模型
图G(E,V)表示交换机网络模型,节点v∈V都有一个物理机,设定网络中的物理机是统一的,每个物理机有资源R(u)(r1,r2,…,rn),ri表示各项分资源。(u,v)∈E表示连接节点u与v的链路传播时延为De(u,v)。网络为具有全局拓扑视图的SDN网络[14],设定网络中的交换机,连接高容量光链路,因此每条链路的带宽容量不做约束[15]。
定义(干扰度):假设两个向量a(x1,x2,…,xn)和b(y1,y2,…,yn)之间的夹角为θ,a、b向量的长度分别是‖a‖和‖b‖,θ所对的边的边长为‖a-b‖。根据余弦定理:
‖a-b‖2=‖a‖2+‖b‖2-
(1)
a·b=‖a‖·‖b‖cosθ
(2)
根据上述公式可以得到:
(3)
cosθ就是余弦相似度,两个向量之间的夹角越小,其夹角余弦越大(越相似)。因此可用余弦相似度来度量两个VNF对资源的需求相似度。向量a(x1,x2,…,xn)对应VNF对各种资源的占有率X(X1,X2,…,Xn),由于不同VNF对每种资源的依赖程度不一,故定义λ(λ1,λ2,…,λn),λi表示VNF对某一种资源依赖程度的权值。VNF间的干扰度定义如下:
(4)
其物理概念为同一服务节点中的一个VNF的资源的占有率与另一个VNF对资源的实际需求率的一个契合程度。网络吞吐量与网络中VNF间的干扰程度呈反比例关系,定义反比例系数β,吞吐量P(m)与干扰度存在下述关系:
P(m)=βcosXY
(5)
决策变量的定义:用F表示所有流的集合,用Z表示网络中VNF个数。任意一条流f∈F由三元组(srcf,dstf,Mf)表示其属性,其中srcf表示流f的源节点,dstf表示流f的目的主机,Mf表示流f需要经过的VNF集合。ratio(m)表示VNFm的流改变因子。用符号→来定义VNF的依赖关系,若m→n则n依赖于m,即业务流需先经过m再经过n。
首先定义VNF处理顺序的传递性,例如m→n,n→k,那么m→k。用二进制变量d(m,n)来描述这种关系:
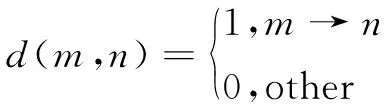
(6)
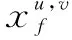
(7)
(8)
流f在网络中经过的是一条多跳路径,用i表示跳数,若共有N跳,那么1≤i≤N。用f(u,i)表示第i跳所在的位置:

(9)
同一节点允许部署一条流的多个VNF实体,对于流f来说有以下情况:
∃u,i≠j:f(u,i)=1&f(u,j)=1
(10)
约束条件:tin(f,u)和tout(f,u)分别表示流f进入节点u和流出节点u的流量数据率。对于流f来说,如果它在节点u经过了VNF的处理,那么tin(f,u)和tout(f,u)满足如下关系:
(11)
对于网络中的物理节点来说,所有服务请求的VNF集合实例化到该点上所需的资源总和必须不超过该物理节点u所能提供的节点容量,R(u)与式(4)中的Xi以(Yi)对应,约束如下:
(12)
构成一条路径的所有中间链路De(u,v)之和要小于所设定的时延容限MDe。约束如下:
(13)
如果VNFn依赖于VNFm,那么流f将先经过VNFm,即有以下约束:
f(v,k)×i]×d(m,n)>0
(14)
用下式表示链路中的流守恒:
tout(f,u)=tin(f,u+1)
(15)
最后文中目标是最大化网络吞吐量,T表示参数因子,T与tin(f,u)呈反比。
(16)
3 算法分析
该文所要完成的目标,在式(11)~式(15)的约束下求解是一个NP-难问题。因为在所给定的节点容量约束下,不考虑资源种类和各VNF对不同资源的需求权重时,问题将转换成装箱问题,装箱问题是常见的NP-难问题[16]。完成该目标需要两个算法实现,首先通过自主设计的基于贪心的CAPA算法得到VNF间的最佳组合,并进行放置。然后通过TAA算法进行流服务请求调度,使得数据流经过各个节点的累加值最小,进一步减小VNF间性能干扰。所以通过该文提出的两步调整策略可完成目标。
3.1 算法描述
算法1:MIMP算法。
输入:虚拟网络功能集合L,网络拓扑G(E,V),拓扑中心节点c;
输出:组合放置集合L'。
1.构建优先矩阵ψ
2.镜像复制
3.延时接受算法匹配
4.重复项删除
5.干扰度求和排序
6.if原∑P(m)>重组∑P(m) do
7.拆分重组Return to step 5
8.else 构建组合集ξ
9.Dijkstra算法选点
10.组合集映射到节点集
11.得到组合放置集合L'
12.结束
算法1:
(1)输入数据处理:首先输入所有VNF资源需求集合L,网络拓扑G(E,V)和给定的拓扑中心节点c,通过式(4)进行干扰度计算,生成VNF间的干扰度矩阵W。然后将矩阵的每一行元素按照干扰程度大小进行升序排列得到优先列表矩阵ψ,越靠前则最优。复制列表矩阵,一份做原优先列表矩阵,另一份为镜像ψ'。镜像处理使得原先无法进行匹配的单列元素可以进行匹配处理。
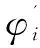
(3)节点映射:由于模型的设定,物理机类型统一,故将VNF组合向网络拓扑中心靠拢,方便后续的服务请求调度,故以延时De为权值,使用Dijkstra算法计算给定节点c到网络拓扑中其他节点延时的大小,得到权值集合τ。将得到的组合集合ξ中的元素映射到权值较小的集合τ中的节点元素,最终输出最佳组合放置集合L'。
算法2:TAA算法。
输入:服务请求的虚拟网络功能集合Ω,网络拓扑G(E,V),组合放置集合L'
输出:服务请求调度集合S
1.while Ω≠∅ do
2.读取所需VNF信息构建初步顺序
3.if 无依赖关系的VNF个数≠0 do
4.if NVF ratio(m)<1 do
5. 序列头部升序排列 end if
6.if NVFratio(m)>1 do
7. 序列尾部升序排列 end if
8. end if return VNF order
9.得到必经点及顺序约束
10.Dijkstra算法
11.if ∑De(u,v) 12.else丢弃此请求 13.输出最终服务请求调度集合S 14.结束 算法2: (1)顺序建立:请求集合Ω不为空,对每条服务请求中的VNF的流修改因子ratio(m)进行读取,判断服务请求中的VNF是否存在依赖关系的VNF,确立具有依赖关系的VNF的流经顺序。然后判断服务请求中的VNF是否存在没有依赖关系的VNF,若有,且VNF的流修改因子小于1,则将其在调度列表中头部进行升序排列,若VNF的流修改因子大于1,则将其在调度列表中尾部进行升序排列,从而确立了此条服务请求中VNF的所有流经顺序。 (2)路径选择:对于每条服务请求读取其源节点以及目的节点,并将其值分别赋予k1,k2根据服务请求所需的VNF所在的物理节点,建立必经点的路径约束,再根据上述处理提供的VNF流经顺序,建立顺序约束。最后通过双约束的Dijkstra算法以链路延时为权值,进行路径选择,若总传播时延超过给定的时延阈值则丢弃此条服务请求,若满足约束则加入到最优路径集,最终为请求集合中的每条服务规划出一条路径,得到服务请求调度集合S。 用ω表示VNF的个数,在算法1中构建干扰度矩阵所需循环次数为O(ω2),构建优先列表矩阵所需循环次数为O(ω2),匹配过程中最大循环次数为O(ω2),重组调整过程中的最大循环次数O(ω2-2ω)。Dijkstra算法时间复杂度为O(v2),v表示物理节点个数,故算法1的整体复杂度为O(v2+ω2)。 在算法2中VNF的顺序处理的复杂度取决于服务链的长度,以及无顺序约束的VNF个数,定义平均服务链长度为ε最终顺序建立的平均复杂度为O((ε/2)2)。Dijkstra算法的时间复杂度为O(n2),其中n表示节点跳数,由于约束条件的存在,算法中使用的Dijkstra算法的复杂度为O(ε2),故其整体复杂度为O(ε2+n2)。 CAPA算法所要解决的是一个NP-难问题,故对此进行近似比分析。将物理机假设为单位容量为C的箱子,VNF假设为大小为s的物品,设si<1,i=1,2,…,n。设OPT(I)为最优解所用箱子数目的一个上界,CAPA(I)为CAPA算法的解。由算法描述中CAPA算法的拆分重组规则可知,所有箱子中至多有一个非空箱子,所装的物体体积小于1/2。 现在设εi为第i个箱子中的空余容量,δi为物品占用第i个箱子的容量εi+δi=C。那么有: 对于第k个箱子有两种情况: (1)εk<δk; (2)εk>δk。 对于情况2,有:εk-1<δk,εk<δk-1,所以: εk-1+εk<δk-1+δk。 最优解的一个上界为所有箱子恰好装入全部物体,即: 故CAPA算法近似比为: 硬件环境为Inter Core i5-7200U CPU 2.71 GHz RAM 4 GB的Windos10家庭版操作系统;该文选择的仿真平台是matlab2017a。实验采用的网络拓扑为真实的网络拓扑Internet2(Internet OS3E)[17]。实验设定VNF个数Z=32,实验考虑多种不同资源R(u)(r1,r2,…,rn),每个VNF对多种不同资源都有不同的权λ(λ1,λ2,…,λn),每个VNF都有一个固有的流修改因子ratio(m)。 4.2.1 CAPA算法的性能分析 图4表示不同算法情况下,网络中分别部署4,8,16,32个VNF时,网络的整体标准化吞吐量变化情况(利用式(5)计算,并做标准化处理,标准化处理最终为两个结果的比值)。从实验结果图中发现,在VNF数量较少的情况下,CAPA算法与First-fit算法[18]差异不是特别明显。这是因为当VNF数量较少时,组合的方式很少,当VNF数量增加使差异不断增加是因为First-fit算法在寻找组合对象时只考虑选择对象对自己的干扰程度,没有考虑自身对选择对象的干扰程度,使得单方面最优,达不到双方最优。图中random表示不考虑干扰因素以随机的方式组合,其代表的柱型起伏不定的原因是由于VNF数量少时偶然性因素较大。 图4 不同VNF个数下的网络标准化吞吐量情况 4.2.2 TAA算法的性能分析 图5表示在Internet OS3E网络中,设定服务链总长度为10,当平均无依赖关系的VNF占服务请求链的百分比增加时,两种算法情况的对比。纵坐标的标准化处网络吞吐量,可由式(16)经过标准化处理得到。从图中可以看出,当服务链请求中的无依赖关系的VNF占总体服务链请求所需的VNF比重越小,TAA算法性能会越接近于Dijkstra算法[19],这是因为当具有先后依赖关系的VNF占服务链请求所需的VNF比重越大,TAA算法所能调整的范围就会越小,在服务链请求中的VNF全部相互依赖的情况下,TAA接近普通算法。在实际情况中服务链请求中的VNF是有相当一部分可以调整的。 图5 无依赖关系的VNF比例与性能间关系 4.2.3 标准化传播时延分析 图6表示在不同的无依赖关系的VNF比例下,两种VNF放置方法与网络标准化传播时延的关系,其中服务链总长度设定为10,用TAA算法进行调度。图中可以看到随着流经顺序可调的VNF比例的增加,两种放置方法对应的网络中标准化传播延时都在减小,这是因为服务请求调度的顺序约束减少了。而中心化放置方式对应的网络标准化传播时延,始终较小的原因是由于随机放置,会使得某些VNF被放置在网络边缘,流服务请求必须达到网络边缘获取相应的处理,仿真结果中随机放置情况下TAA算法所得平均端到端延时为0.55 ms。而中心化放置使得VNF集中于网络拓扑中心附近,服务请求在网络拓扑中心附近便可获取所需的处理,实验分析表明CAPA算法中将VNF放置在网络拓扑中心附近,能够在一定程度上减小服务请求调度过程中的网络传播时延。 图6 标准化传输时延无依赖关系VNF比例间关系 4.2.4 算法整体性能分析 图7中,考虑干扰方案表示在Internet2(Internet OS3E)网络中,将VNF通过算法1进行组合放置在网络拓扑中,设定服务链总长度为10,服务链请求中具有依赖关系VNF的比例为60%,并使用TAA算法进行服务请求调度。未考虑干扰方案表示在Internet2(Internet OS3E)网络中,通过First-fit算法进行组合放置,并使用Dijkstra算法进行请求调度。从实验生成图中可以看出,当数据流不断增加时,两种方案下的标准化网络吞吐量都有所下降,但是考虑干扰方案下的网络吞吐量始终比未考虑干扰方案下的标准化网络吞吐量优。 图7 标准化处理能力随数据流大小变化示意图 提出了一种考虑VNF间性能干扰的组合放置问题,并根据VNF的修改数据流大小的特性设计了服务链请求调度算法,从而减小了VNF间性能干扰,提高了网络吞吐量。理论分析以及仿真结果表明,该策略较忽视干扰因素的一般策略可将网络吞吐量提升1.3倍。今后将研究在干扰情况下的动态部署VNF以及如何权衡成本开销与网络性能间的关系问题,并将在真实环境中进行实验以提高结果的准确性。3.2 算法复杂度分析
3.3 算法近似比分析
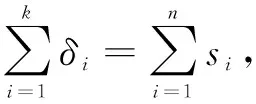
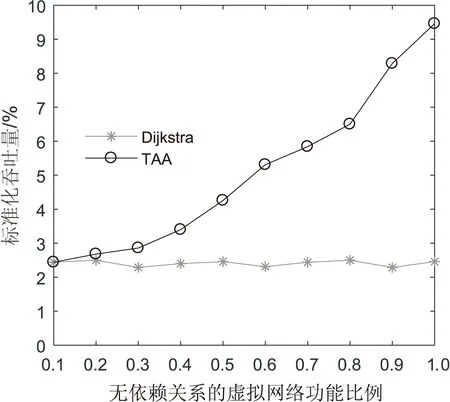
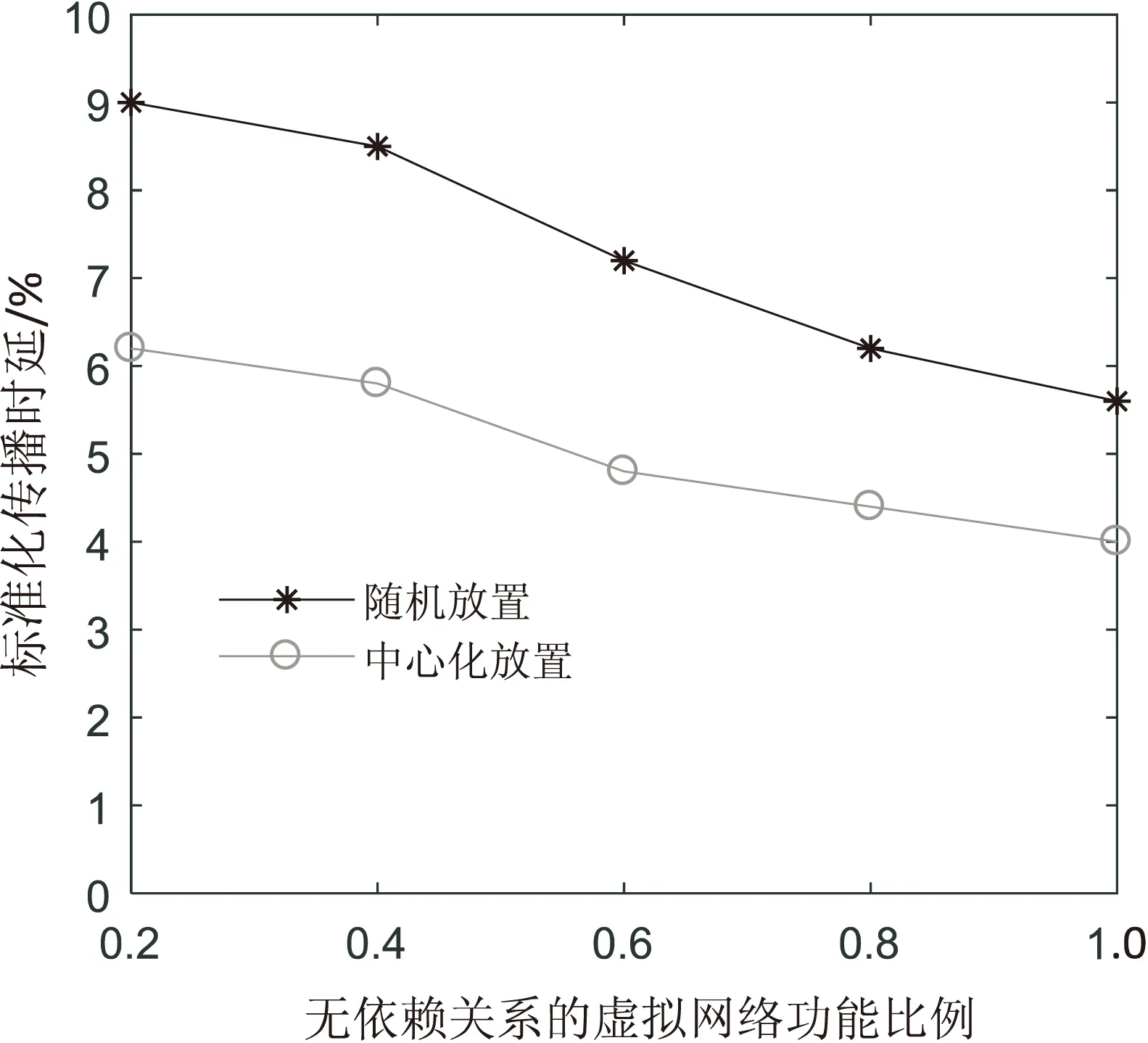
4 仿真实验结果及分析
4.1 仿真实验环境参数
4.2 性能分析


5 结束语
