偏振双向反射分布函数模型研究进展

王 凯，刘 宏，郭奉奇

(1.渭南师范学院 物理与电气工程学院，陕西 渭南 714099；2.宇航动力学国家重点实验室，西安 710043；3.西安交通大学 电子与信息学部，西安 710049；4.陕西信息光子技术重点实验室，西安 710049)

20世纪60年代前，已经存在各种名目的反射率，这些反射率在定义、术语和符号等方面都存在很大差异。因此，许多学者呼吁对众多的反射率进行统一。1977年，NICODEMUS F E[1-2]首次提出了双向性反射特性的表达——双向反射率分布函数，同年美国国家标准局以此为参考定义了标准的双向反射分布函数(Bidirectional Reflectance Distribution Function，BRDF)并将它作为物体表面双向性反射特性的基本表达，从而使反射率定义的研究达到顶峰。

BRDF用于描述目标物体表面的空间光反射特性。其用来描述物体表面的光反射特性具有唯一性的特点，它所确定的反射特性只取决于物体表面本身的特性，表示不同入射条件下物体表面在任意观测角的反射特性。它主要由表面粗糙度、介电常数、辐射波长、偏振等因素决定[3-5]。BRDF能够很好地将材料表面的反射和散射统一于同一概念中，可以描述表面的方向散射和辐射特性。BRDF理论经过发展，已广泛应用于可见光、红外波段和微波波段的散射、辐射方面，在地物遥感[6-8]等领域得到了广泛应用，并已经扩展到计算机视觉等新兴的研究领域。另外，通过BRDF的测量数据获得物体材料的红外反射率也是取得许多不透明材料(尤其在800 K以下)的发射率和吸收率的重要方法。

不同材料光学散射特征的差异在光学特性建模中体现为不同的BRDF表达形式，也就是说事实上，BRDF的确定是描述目标光学散射特性和目标光学散射特性建模过程的关键和核心所在。如果在光与目标表面发生作用的过程中加入入射光和反射光的偏振态信息，将传统的标量形式BRDF扩展为穆勒矩阵形式的偏振双向反射分布函数(polarimetric Bidirectional Reflectance Distribution Function,pBRDF)，就可以将反映入射光和反射光偏振信息的Stokes矢量对应联系起来，反映目标表面的全偏振特性，完整地描述和表示目标表面的偏振特性，从而获取我们感兴趣的材料特征信息。

1 偏振BRDF模型的研究现状

1.1 国外偏振BRDF模型研究情况

国外关于pBRDF模型的研究虽然开展得比较早，但发展较为缓慢。20世纪90年代末，一些学者的相关研究表明，还没有一个合适的pBRDF模型能够以满足我们要求的精度来描述pBRDF特性。但是先前的一些标量BRDF，实际上已经提出了建立pBRDF模型的思想。

1995年，美国尼科尔斯研究中心和佛罗里达埃格林空军基地的FLYNN D S和ALEXANDER C[9]针对以前BRDF与光的偏振状态之间关系描述的不足，首次将全偏振的表达方式引入BRDF之中，提出了全偏振BRDF思想。作者将BRDF中的入射光和反射光定义为矢量，并定义了偏振BRDF矩阵，研究了BRDF矩阵和散射振幅矩阵之间的关系，对偏振和非偏振的BRDF表达式之间的关系进行了讨论。该研究虽然没有与具体的BRDF模型结合起来，但它为全偏振形式的BRDF模型研究提供了全新思路和理论基础，对于偏振BRDF的发展具有里程碑式的意义。

Torrance-Sparrow模型(T-S模型)和Beard-Maxwell模型(B-M模型)等许多已提出的BRDF模型均考虑多次散射并假设体散射偏振态是完全随机的，这些模型认为首次表面反射光中包含所有偏振信息。美国密歇根环境研究所的ELLIS K K提出了光滑涂层模型(Glossy Coating模型)[10]，光滑涂层模型的分析型表达式表明体散射部分对偏振是有贡献的，而且发现在一些简单的模型中首次表面反射光与体散射光间是有耦合作用的，并且该耦合作用会对体散射光部分的偏振效应产生影响。

密歇根环境研究所开发了一个基于第一原理的油漆反射模型(F-BEAM)。这种模型能够预测多层涂层的偏振BRDF。[11]与光滑涂层模型相比，F-BEAM在一定领域能解决更复杂的问题。但在其他领域，ELLIS K K发现F-BEAM模型所利用的简化的设想并不总是有效的。因此，在大角度时将会偏离测量数据。

从2000年开始，许多研究者开始对T-S模型这种最典型和常见的BRDF模型进行扩展，将其扩展成为具有全偏振形式的pBRDF模型，并基于全偏振形式的pBRDF开展了相关的应用研究。

2000年，美国海军研究实验室的PRIEST R G和国家标准技术局的GERMER T A[12]将T-S模型与穆勒矩阵结合起来，对一个微面元进行研究，实现了T-S BRDF模型的偏振化，提出了Priest-Germer pBRDF模型(简称P-G模型)。图1为偏振双向反射过程的几何关系图。在图1中：(θi,φi)和(θr,φr)分别代表入射光和反射光的方向；θ和φ分别代表天顶角和方位角；α为宏观面法线方向Z与微面元法线方向n之间的夹角；β为入射方向与微面元法线之间的夹角。并有

图1 偏振双向反射几何关系

(1)

cos2β=cosθicosθr+sinθisinθrcos(φi-φr)。

(2)

P-G模型使用微面元理论，认为它们在二维平面上是高斯分布的，在这样的假设下进行偏振辐射的计算，对其中的角度关系进行了详细描述，并推导出角度关系间的变换矩阵，建立了入射方向、反射方向、微面元法线方向、目标宏观表面法线方向之间关系的四个坐标系：(1)由ri和z构成的坐标系；(2)由ri和n构成的坐标系；(3)由rr和n构成的坐标系；(4)由rr和z构成的坐标系。

给出了坐标系转换矩阵，规定坐标系(1)旋转γi角度至坐标系(2)，坐标系(3)旋转γr角度至坐标系(4)，则有以下关系：

(3)

(4)

坐标的旋转角γi,γr可由下面的关系得到：

(5)

(6)

并由此推导出描述入射与反射偏振光之间关系的琼斯矩阵，给出了穆勒矩阵元素与琼斯矩阵元素之间的关系，得出了包含全偏振信息的T-S pBRDF模型。

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

通过以上关系可以得到表面反射过程的16个穆勒矩阵元素Mi,j(θi,θr,φr-φi)，将标量T-S BRDF表达式中的菲涅尔反射率F换成穆勒矩阵元素Mij，就可以得到全偏振形式的矢量pBRDF表达式，标量形式的BRDF就变成了含有16个元素的矩阵形式的矢量pBRDF表达式。对有绿色涂层的金属样品分别在可见和红外波段进行偏振光主动照明，该模型与实验测量数据能够较好地吻合。

P-G模型表达式：

(23)

其中：σ为表面粗糙度参数；M为微面元的穆勒矩阵；i，r分别代表微面参考系中的入射和反射方向。

P-G模型仅仅修正了T-S BDRF中的镜面反射部分，而且该模型比较明显的一个缺点是当入射光掠入射到目标表面时，在大反射角度处的pBRDF值会趋于无穷大，这是不符合物理规律的。WELLEMS D等人[13]提出了漫射消偏作用。对一个给定粗糙度的全反射微面元，在整个半球上对BRDF积分。积分值与1之差可以归因于光的多次反弹和表面相互作用造成的漫反射。这种消偏是表面粗糙度的函数，而与材料复杂的折射率无关。这种消偏已经加入到DIRSIG中的T-S BRDF模型中。

2002年，PRIEST R G等人[14]又研究了红外波段下高吸收率和高反射率粗糙表面的偏振散射特性，通过分别对带有黑色涂层的阳极化铝以及有等离子体喷铜和镀金的铝衬底的两种粗糙表面进行实验测量，获取了目标表面的穆勒矩阵并与菲涅尔定律进行了比较，发现具有高吸收率的粗糙表面比高反射率的粗糙表面具有更高的偏振度。罗彻斯特理工学院的MEYERS J P[15]在其博士论文中将P-G模型引入了DIRSIG软件。基于复杂环境下的红外散射和辐射的偏振测量，FETROW M P给出了T-S BRDF模型的偏振修正模型[16]，研究了确定材料复折射率和粗糙度的方法，在美国科特兰空军基地和埃格林空军基地对空中目标进行了实验测量并对结果进行了比较。与T-S模型的pBRDF类似，B-M模型也可以通过菲涅尔反射公式经过修正成为偏振形式的BRDF，来预测初次表面反射中的偏振信息。CONANT J A和IANNARILLI F J[17]在其研究中给出了Sandford-Robertson BRDF模型的偏振形式，通过对菲涅尔公式的扩展，加入了对偏振态的描述。根据物理推导，模型将镜面反射分量看作是有偏振的(由于微面元的菲涅尔反射)，将漫反射看作是消偏的(由于多次体散射)，也就是说，材料的偏振性质只存在于表面部分，或者说只依赖表面反射作用。

2003年，美国约翰霍普金斯大学的DUNCAN D D等人[18]提出了一个新的基于物理原理的分析BRDF模型，它能够反映任意粗糙表面散射光的偏振态差异，体现目标的偏振信息。该模型含波长参数，既包含目标表面的固有属性(如折射率)，又包含目标的外在特征(如表面高度变化的统计矩)。该模型的成果之一是它能够预测随光波长变化的辐射偏振态，但其包含的偏振态也仅限于正交的两个方向，即p光和s光。

2009年，怀特—帕特森空军基地的HYDE M W等人[19]对基于T-S模型的偏振BRDF模型进行了扩展，其认为表面微面元的法向分布满足以下关系：

(24)

式(24)中的α即为微面元法向与宏观法向的夹角，ι为表面自相关长度。文章使用由Blinn提出的简化形式的阴影与遮蔽衰减因子G的表达式：

(25)

偏振BRDF的表达式如下：

(26)

(27)

式(27)与P-G模型的一个重要区别就是该模型增加了阴影/遮蔽函数G，G所起的一个关键作用就是保持pBRDF有界。

HYDE M W通过推导得出了解析的漫反射分量的表达式，减少了经验参量漫反射系数：

(28)

(29)

(30)

ρDHR(θi;σh,ι)为方向性半球反射率，经材料表面反射到整个半球上的总能量与沿某一特定方向入射的总能量的比值。该模型中的漫反射分量有两个特点：一是其仅取决于入射角和粗糙表面的统计特性；二是不需要模拟漫反射pBRDF的拟合系数。这个系数普遍应用于其他BRDF中，而其值通常需要通过测量数据与BRDF拟合确定。

考虑镜面反射和漫反射部分：

(31)

Fjk(θi,θr,φ;σh,ι;η)=Fjks(θi,θr,φ;σh,ι;η)，j,k≠0。

(32)

因为漫反射是消偏的，所以漫反射部分只对pBRDF穆勒矩阵中的F00部分有贡献。

Hyde模型有两个特点：一是增加了阴影/遮蔽函数，使得pBRDF有界；二是发展了漫反射pBRDF部分，这部分仅仅依赖于物理参数，不需要与测量值拟合。Hyde模型虽然在镜面反射部分加入了阴影/遮蔽函数，使得P-G模型在近掠射角条件下大反射角度处的pBRDF值得到明显下降，但是在下降过程中有一个突变的拐点也是不符合物理规律的。针对这一问题，西安交通大学的研究人员提出了积分型阴影/遮蔽函数[20]，结果表明加入积分型阴影/遮蔽函数后，大反射角度处的pBRDF曲线平滑缓慢地下降，该方法很好地解决了这一问题。

1.2 国内偏振BRDF模型研究情况

国内在pBRDF模型建立方面虽然较国外发达国家而言还有较大的差距，但是也取得了一定的成果。合肥工业大学的研究人员在一阶矢量扰动理论的基础上，对多层涂层建立了pBRDF模型，并在该模型基础上研究多层高反射和单反射涂层的偏振反射特性[21]。北京理工大学的王霞等人[22]在Hyde pBRDF模型的基础上提出了红外pBRDF模型，并对绿色和黑色油漆表面的偏振反射特性进行了实验测量。

2008年，中国科学院环境光学重点实验室的冯巍巍等人[23]采用基于T-S模型的pBRDF模型，对涂层材料的空间光散射理论进行了数值模拟，采用遗传算法对偏振双向反射分布函数模型的参量进行了反演，分析了模型参量对偏振双向反射分布函数的影响。数值模拟的结果和实验结果的对比说明，该模型算法具有较高的模拟精度，为后续涂层目标偏振特征提取与识别工作提供了一定的参考。西北工业大学的陈超等人[24]通过分析偏振BRDF与实验探测角、波长间的关系，提出用多项式模型来定量描述偏振度分量，在可见光范围内实现偏振光谱BRDF建模，对于土壤等各向性质较为均匀的背景能较好地达到精度要求。2010年，陈超等人[25]从获得的户外试验测量数据入手，分析与探测角、波长之间的关系，通过比较测量的方法得到绿漆涂层木板的可见光谱pBRDF。

2009年，北京理工大学的马帅等人[26]将含有双参数的柯西分布替代常规高斯分布引入微面元BRDF模型，同时考虑了目标自身辐射强度的方向依赖性，在此基础上推导了长波红外偏振的数学模型，并在合理范围内对模型做简化与修正使之适用于仿真研究，并对数学模型双参数σ和q(σ为材质粗糙度参数,q为与材质特性有关的常量,q的引入增强了微面元模型的灵活性)的选择进行理论分析并验证了该模型的灵活性以及优势所在。偏振场景仿真结果较为理想，得到的目标红外偏振特性与实际图像基本吻合。

2010年，北京师范大学的谢东辉等人[27]利用长春光机所研制的多角度观测装置测量了玉米嫩叶、玉米成熟叶和一品红叶表面的双向偏振反射率分布，发现叶片表面反射具有明显的非朗伯性。通过借鉴Cook-Torrance光照模型的形式，将不同偏振态的菲涅尔因子耦合到模型中，推导得到用于叶片表面偏振的双向性反射分布函数模型。将建立的pBRDF模型与实测数据拟合，利用遗传算法进行参数反演，获得叶片漫反射率、等效折射率和表面粗糙度的大小。

2011年，哈尔滨工业大学的陈加伟[28]研究并建立了偏振反射率模型，采用植被和土壤的物理模型进行仿真，也对半经验模型进行了深入分析和进一步拓展，实现了偏振高光谱的场景仿真。

2017年，西安交通大学的朱京平课题组先后提出了适用于金属材料[29]和空间目标材料[30]的pBRDF模型。该模型通过研究光与目标材料的相互作用过程，首次提出将目标反射光分成镜面反射光、方向性漫反射光和理想漫反射光三部分(三分量假设)，如图2所示。

图2 光与目标材料的相互作用过程

镜面反射光是由入射光与金属材料表面发生作用后的单次反射光形成，该部分遵循微面元理论和菲涅尔定理，如图3所示。假设材料表面是由很多高低起伏的表面微元组成，每一个小微元可以看作一个小镜面，所以每一个微面元满足Snell反射定律。所有小微面元都是随机分布的，并且微面元斜率的概率统计分布服从高斯分布函数。入射光照射到不规则的表面上，在每一个小微面元都会发生镜面反射。镜面反射部分的BRDF表达式可以通过微面元理论推导得到。

图3 镜面反射分布情况

方向性漫反射部分是入射光经凹凸不平的表面多次反射后形成，如图4所示。由于多次反射的计算非常复杂，所以方向性漫反射部分在现存的模型中都是被认为在整个半球空间均匀分布的。然而多次反射的反射角是与入射微面元的倾斜角相关的，根据微面元理论，微面元分布服从高斯分布，因此多次反射也应该服从特定的分布。

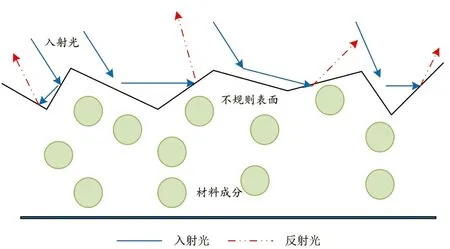
图4 方向性漫反射分布情况

理想漫反射是由入射光进入材料下表面与材料内部粒子发生多次相互作用后，由上表面透射出来形成，如图5所示。入射光子与材料内部的粒子发生相互碰撞，每一次相互作用都会使入射光的方向和偏振态发生改变，所以方向性漫反射的偏振态也是随机分布的。但是相互碰撞后光子沿每一个方向移动是等概率的，所以认为理想漫反射光沿每一个方向都有相同的强度，也就是该部分在整个半球空间是均匀分布的。

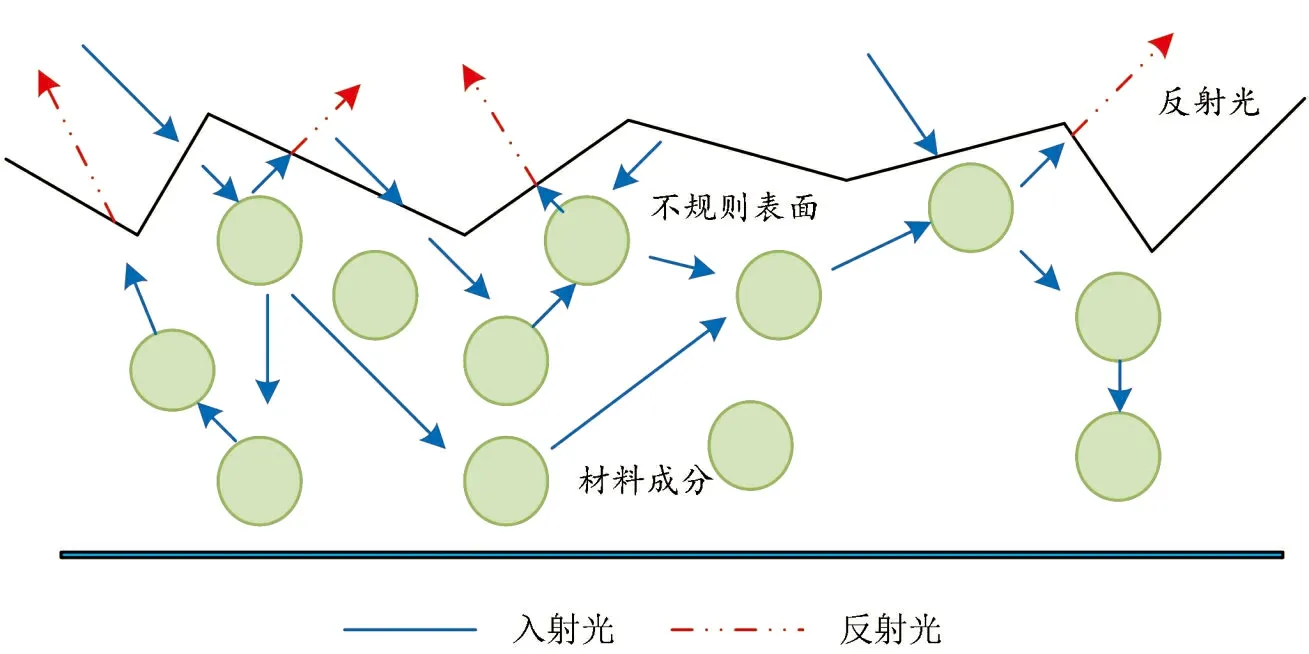
图5 理想漫反射分布情况

通过对不同种类的目标材料和具有不同粗糙度的同种目标材料的实验测量数据进行拟合得到最优化的表达式，理想漫反射光部分遵循朗伯定律。

根据三分量假设，从入射光的Stokes矢量出发，建立了入射光Stokes矢量、反射光Stokes矢量与pBRDF穆勒矩阵之间的关系，就此反推出新的pBRDF穆勒矩阵，并建立了pBRDF模型，镜面反射光由表面单次反射光形成，携带了光与材料相互作用后获得的所有偏振信息；方向性漫反射光由光经凹凸不平的表面多次反射后形成，理想漫反射光由入射光子进入材料与内部粒子发生相互作用后的体散射光形成，这两部分反射光完全消偏。通过对不同的金属材料以及具有不同表面粗糙度的同种金属材料的实验测量数据和模型仿真结果对比可以看出，三分量pBRDF模型能和实验测量结果较好地吻合。从对比结果可以看出，对具有不同粗糙度的同种材料来说，反射光中3分量的比例不同。对于不同种类的材料，模型中的3个分量系数的比例也是不同的。三分量的比例既随着材料的不同而变化，也随着粗糙度的不同而变化，该模型在理论上更加合理。并且通过两种模型与实验测量结果对比后的误差分析验证了三分量模型在精度上较原来的模型有很大的提高。该课题组还在三分量pBRDF模型的基础上进一步提出了体现材料表面粗糙度影响的偏振度表达式。[31]

2 需要解决的关键问题

(1)虽然人们对pBRDF的研究比较多，建立的模型也有很多种，但是尚未见到有文献对各种不同pBRDF模型的适用条件(如适当的材料、波段等)进行完整的总结和讨论，进而为材料检测、目标识别提供一个光学散射模型的选择依据，这样就造成人们在进行光学散射建模的过程中存在一定的盲目性，并且目前典型的pBRDF模型对于温度等影响因素没有加以考虑。

(2)目前所有的全偏振双向反射模型pBRDF都要依赖基于实验测量的任意角度下的穆勒矩阵，穆勒矩阵完全由实验确定，测量过程复杂，导致pBRDF依赖测量和经验，缺乏按照电磁理论推导的物理来源，使得利用模型对偏振双向反射特性进行预测时并不能减少实验测量的工作量，也就是说，这样“查表”形式的pBRDF模型实际上不是完整意义上的模型。目前，进行完整意义上的全偏振pBRDF模型建立，难点在于对16个穆勒矩阵元素的描述，但是目前国际上对穆勒矩阵元素的研究成果比较少，人们对其物理含义和规律的认识仍需加强。

(3)目前国内外对目标偏振特性机理和规律的研究较少，这使得人们对目标的偏振散射特性深层次的物理机理理解仍然不够深入，相关研究偏重于通过实验得出效果进行比对。由于对偏振效应物理机理方面研究成果的缺乏，使得国内外学者在研究目标偏振特性时，只能依靠经验数据进行分析，缺乏理论指导。

3 总结与展望

偏振探测与传统的光强探测相比有着明显的优势。无论在国外还是国内，偏振技术的研究与应用发展很快。目前各国的研究人员正在更宽的波段对偏振特性进行研究，并且研究对象从目标识别向生物组织特性等热点方向扩展。随着相关学科技术的发展和人们对偏振特性在目标识别等场合应用的持续关注，目标偏振双向反射分布函数建模及偏振散射特性研究必将取得更丰硕的研究成果。目标偏振双向反射分布函数建模及偏振散射特性研究将有以下几个方面的发展：(1)穆勒矩阵深层物理含义和变化规律仍有很大的研究价值，明确穆勒矩阵中每一个元素代表的物理含义，研究每一个元素关于空间角度和其他影响因素(内因和外因)的函数表达式，从而获得准确的pBRDF模型解析表达式，完成对目标表面的全偏振信息建模。(2)总结不同条件下pBRDF的适用范围，由于不同的材料表面具有不同的偏振双向反射分布特性，描述不同的材料表面要选择不同的pBRDF模型，所以对各种不同形式的pBRDF模型的适用条件(材料、波段、表面分布特性等)进行完整的研究和总结，能够为目标识别、材料检测、大气传输等不同过程提供pBRDF模型的选择依据，使得人们进行光学散射建模时选择pBRDF模型有据可依。(3)从物理本质出发，通过理论推导研究所有影响目标偏振特性的内部本质属性和外界环境因素，找出他们对偏振特性产生影响的规律，进而揭示产生目标偏振特性的最本质原因，对今后在目标偏振特性方面的研究和应用起到推动作用。