智能网联环境下交叉口混行车队通行模型构建
2021-01-18刘天天陈思祺刘洪廷
刘天天,莫 磊,陈思祺,刘洪廷,张 钊,2,丁 川
(1.北京航空航天大学交通科学与工程学院,北京 100191;2.交通运输部公路科学研究院,北京 100088)
0 引言
随着自动驾驶技术和车联网技术的快速发展,过去极具挑战的城市道路交叉口交通控制问题有了新的解决办法[1-4]。然而,自动驾驶汽车全面落地面临诸多困难,在未来很长一段时间内,将会面临自动驾驶车辆(Connected and Autono⁃mous Vehicle,CAV)与网联车辆(Connected Ve⁃hicle,CV)混行的环境。为解决在不同CAV 渗透率条件下的交叉口通行权优化问题,对智能网联环境下交叉口混行车队的通行问题进行研究很有必要。
近年来,国外学者关于智能网联环境下的混行交叉口通行模型进行了大量研究,如Szilassy等[5]提出基于神经网络的交叉口信号控制模型;Barthauer 等[6]采用分离的方法保护自动驾驶汽车,提出自动驾驶汽车渗透率较低时的保护运动方案;Yang 等[7]提出启发式算法切换信号控制并对自动驾驶车辆进行轨迹优化,以有效减少停车次数和延时;Zhao 等[8]采用模型预测控制(Model Predictive Control,简称MPC)方法协同车辆间距,降低能耗;Talebpour 等[9]提出混行交通的微观仿真框架。然而,以上研究均假设CV 能接受驾驶速度建议,这与实际情况存在较大偏差,同时所建模型计算时间偏长,难以满足混行车队在交叉口通行的实时计算要求。
国内学者对智能网联车辆在交叉口的通行也作了一些研究,如Feng 等[10]构建了针对CAV 的阶段性信号模型;Yu 等[11-12]建立了单交叉口信号配时和车辆估计优化的真实集成模型;Xu 等[13]提出在进行交通信号优化的同时控制车辆速度的方法。然而,现有研究未充分考虑人工驾驶的网联车辆,难以解决混行车辆编队情况下交叉口的通行权问题。
鉴于现有研究存在的不足,本文将针对混行交通,考虑实时性要求,采用混合整数规划方法对不同CAV 渗透率和不同速度建议接受概率下的交叉口运行指标展开研究,同时通过车辆编队、信号配时实时优化和车辆轨迹引导三个模型,实现对交叉口交通运行安全、高效地控制。
1 智能网联环境下交叉口混行车队通行模型构建
1.1 建模条件
本文研究场景为标准的四进口道交叉口,每个方向为双向六车道,如图1(a)所示,无线通信技术V2X(Vehicle to Everything)覆盖以交叉口为中心、以R为半径的区域;交叉口每个车道设定为固定转向,如图1(b)所示,车辆在进入不可变道区之前可换道,右转方向始终绿灯。
本模型构建基于以下假设:
(1)在覆盖区域内,V2X 通信没有丢包现象,交叉口控制中心(Intersection Control Center,ICC)可接收CV和CAV 信息(如速度、位置和加速度等)并控制所有CAV 轨迹,且给CV 轨迹建议;
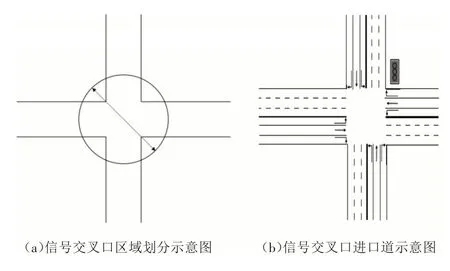
图1 交叉口场景示意图
(2)CV为人工驾驶网联车,且以一定概率接受速度建议。
1.2 建模假设
本文以混行车队为基本控制单元,并基于以下假设建模:
(1)车辆换道:车辆在进入不可变道区之前变道,具有相同转弯需求的车辆在可变道区行驶到同向车道;
(2)混行车辆编队:CAV 与CV 根据车辆跟驰条件在不可变道区组队,CV 根据一定概率接受建议加入车队;若CV 没有听从建议而滞后,后方来车判断跟驰条件选择是否组队,或该CV单独成为一队,并进入下一优化周期;
(3)头车向ICC发送信息:头车将状态位置、加速度、速度、车队的车辆数等信息发送给ICC;
(4)ICC优化及引导车队:ICC根据车队信息运行信号灯控制优化模型,将绿灯时间分配给不同的车道,发送行驶建议给混行车队,若CV 没有听从建议,则再次被ICC 检测,进入下一个优化周期。
1.3 混行车辆编队模型
车辆进入不可变道区域后,具有同样方向的车辆组队作为控制单元。车辆编队条件如下:
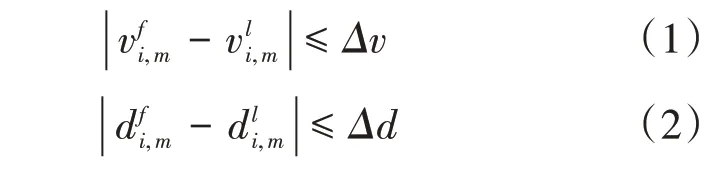
式(1)~式(2)中:为车队P(i,m)的跟随车辆速度;为车队P(i,m)中头车的速度;P(i,m)表示车队在i进口道(i=1,2,3,4,分别表示南、东、北、西进口道),方向为m(m=1,2,3,分别表示左转、直行、右转),如P(1,3)表示南进口右转车队;Δv为速度阈值;,分别为车队P(i,m)中头车和跟随车辆到停止线的距离;Δd为距离阈值。
式(1)和式(2)表明,前车和后方跟随车辆同时满足以下两个条件时即可组队:
(1)相邻车辆的速度差小于Δv;
(2)相邻两车的间距小于Δd。
组队后,车队P(i,m)中的车辆数发生如下变化:
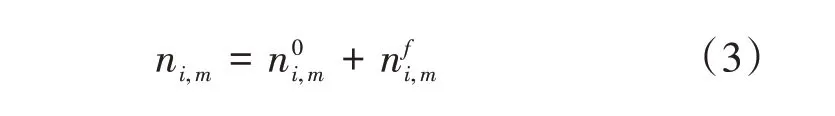
式(3)中:ni,m为组队后车队P(i,m)中的车辆数;为组队前车队P(i,m)中的车辆数;为车队P(i,m)后面跟随的车量数。
车辆在跟驰过程中的安全速度基于改进的Krauß模型[14],按下式计算:
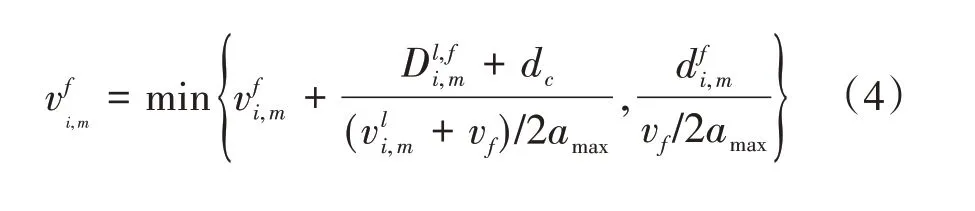
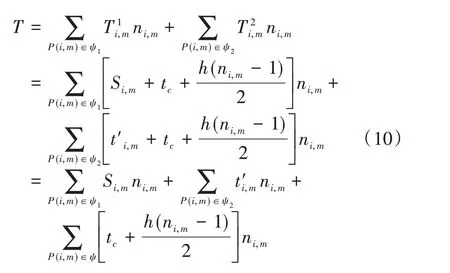
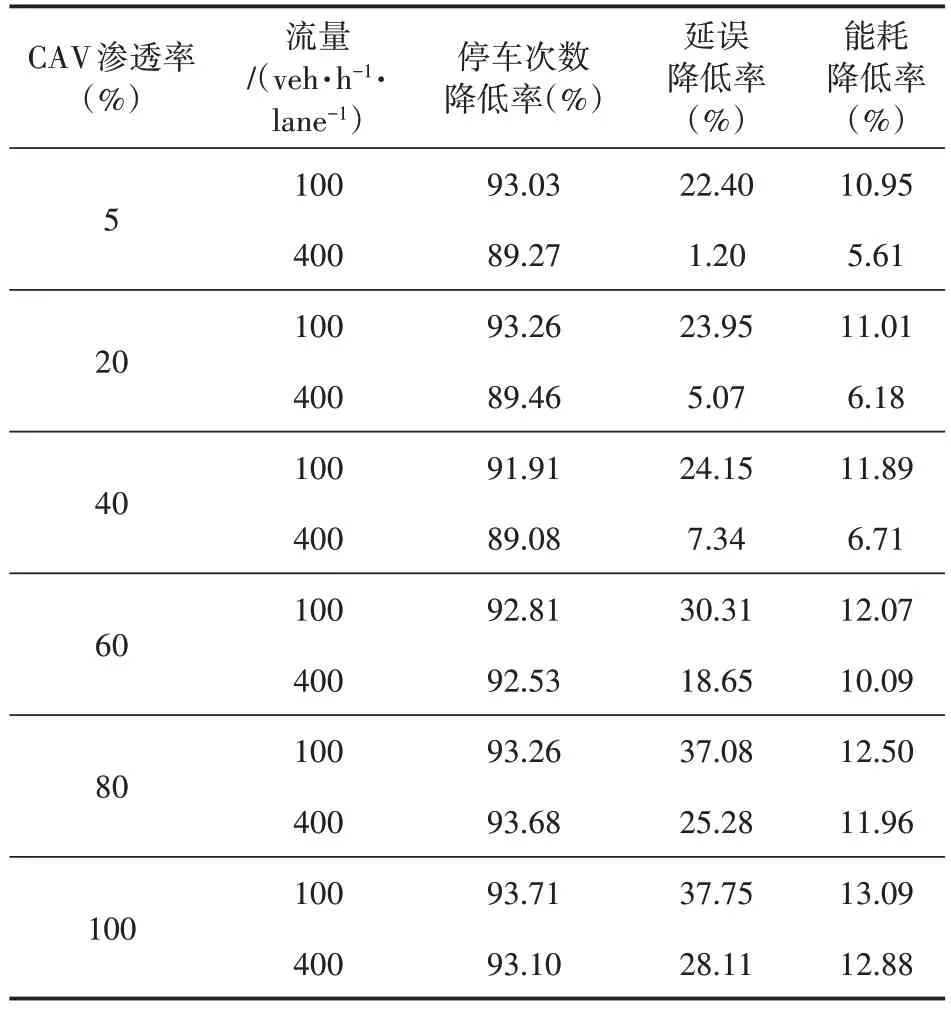
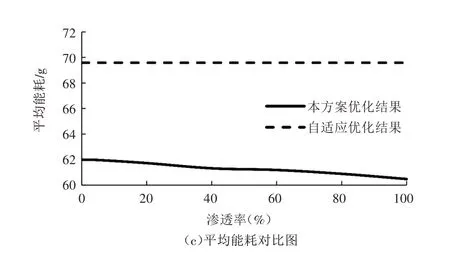
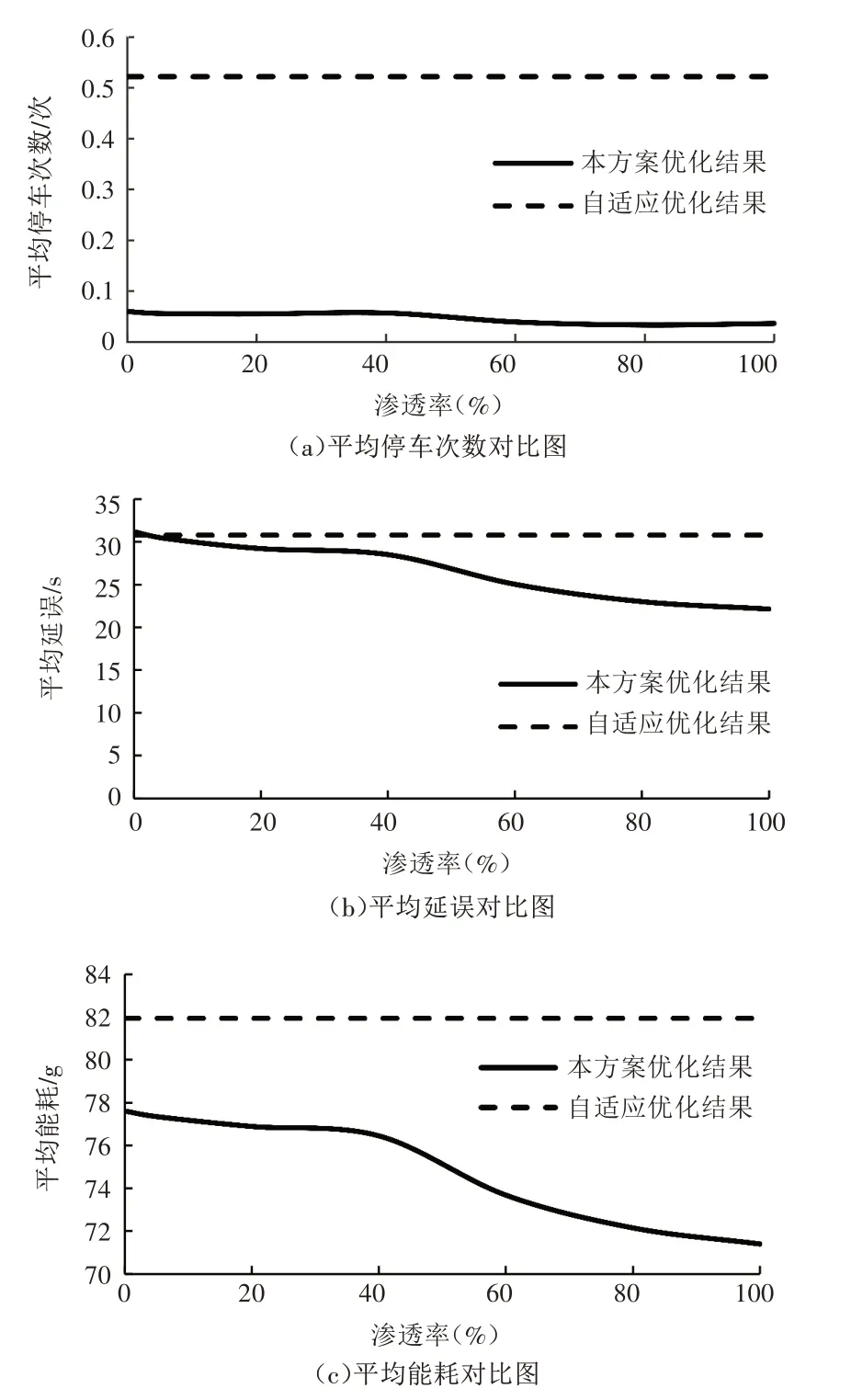
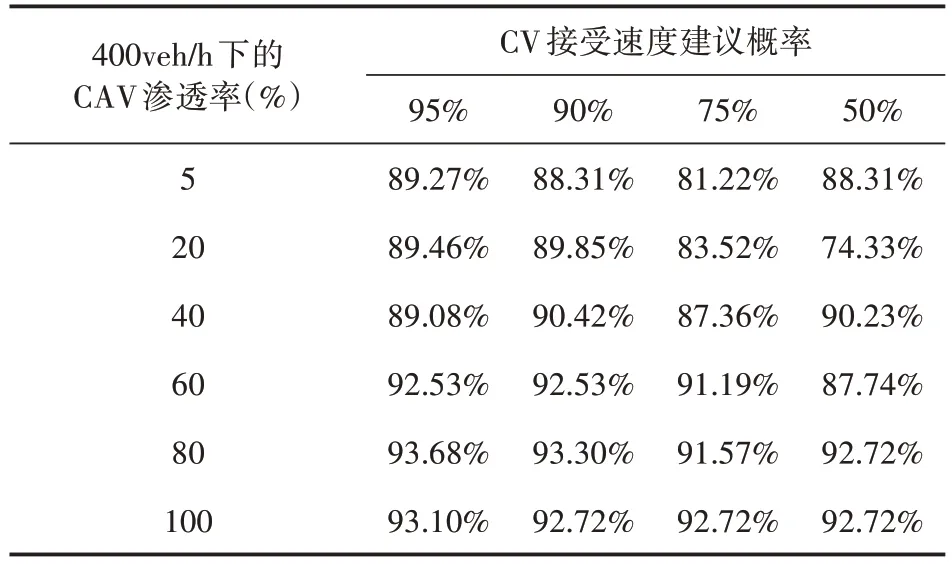
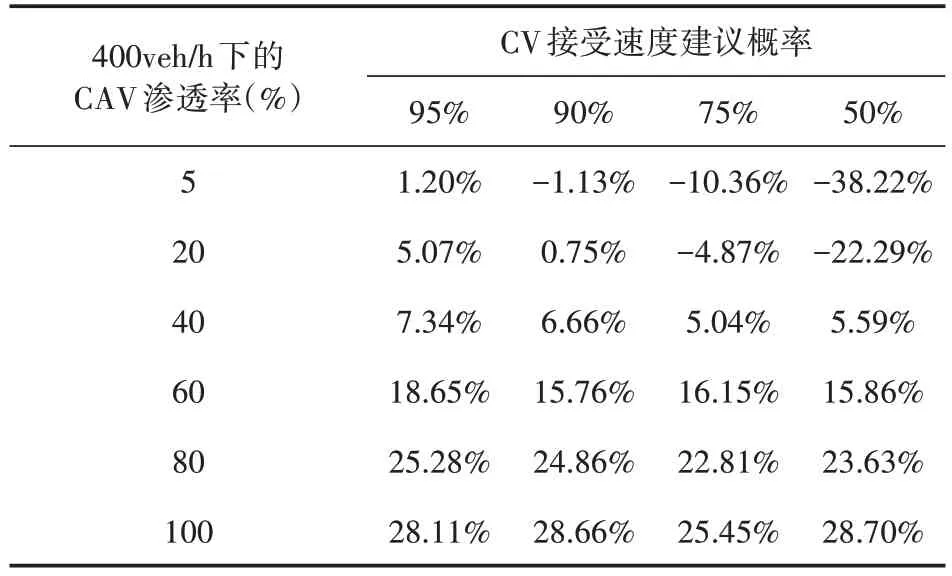
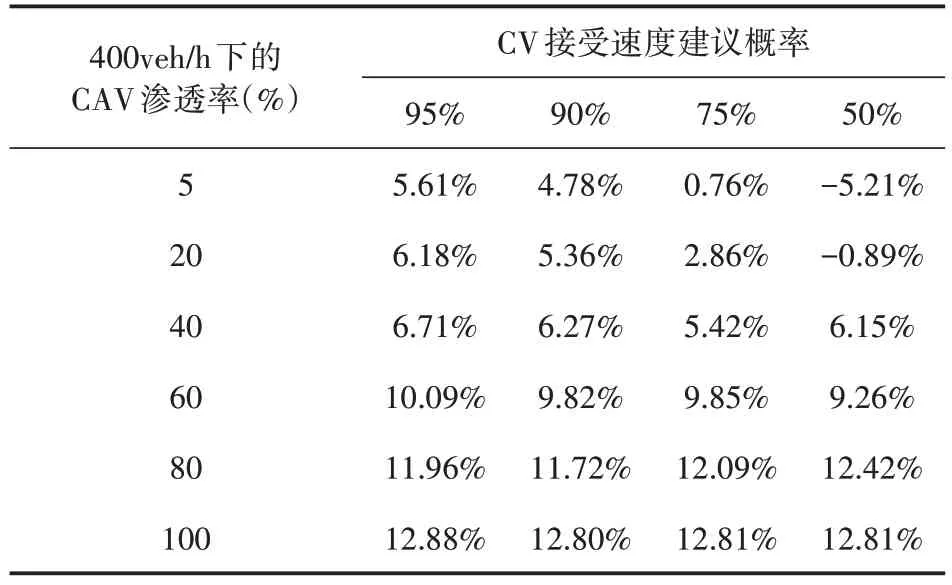
式(4)中:为车队P(i,m)头车与后面跟驰车辆的距离;dc为预设的安全距离;vf为自由流速度;设vi,m为车队速度,则车队P(i,m)速度小于自由流速度,即vi,m 对于混行车辆的编队,分为以下3种情况: (1)CV 为头车,人工驾驶车辆对速度建议及组队建议的执行可能存在一定的误差,会出现CV 作为头车时与后方车辆间距较大的情况,如图2(a)、(b)所示; (2)CAV 为头车,CV 跟在车后或在CAV 之间,如图2(c)、(d)所示; (3)CV 在车队后时没有听从组队建议,分为两种情况:CV 单独为1 个车队,或CV 与后车组队,如图2(e)、(f)所示。 图2 不同编队示意图 模型的理想优化目标为车队P(i,m)抵达停止线时可直接通过交叉口,若有某两组车队距离停止线都很近,或车队到达停止线的时间间隔很短,此目标就难以实现。因此,基于交叉口通行效率最优的原则,将优化目标设为最小化所有车辆的通行时间。 1.4.1 车辆行程时间计算 车队P(i,m)抵达交叉口停止线时有两种可能情况: (1)车队P(i,m)到达停止线时信号灯未变为绿灯,须在停止线停车等待,即P(i,m)的绿灯开始时间在车队减速直到在停止线停止的时间之后: 式(5)中:为车队P(i,m)减速直到在停止线停止的时间;Si,m为车队P(i,m)的绿灯开始时间。 车队从开始到通过交叉口的行程时间等于到达停止线的时间、在停止线的等待时间及穿过交叉口的时间之和。假定车队P(i,m)以饱和流率穿过,则通过交叉口的时间可用下式计算: 式(6)中:为该情况下车队P(i,m)从开始到通过交叉口的行程时间;tc,h为常数,分别表示头车经过交叉口的时间和车头时距;其他变量意义同前。 (2)车队P(i,m)到达交叉口时信号灯已是绿灯,可不停车通过,即车队P(i,m)到达停止线时绿灯已经启亮: 式(7)中:为车队到达停止线的时间;其他变量意义同前。 为保证车队P(i,m)中所有车辆可在剩余的绿灯时长内安全穿过交叉口,须满足以下条件: 式(8)中:Gi,m为车队P(i,m)的绿灯持续时间;其他变量意义同前。 在该情况下,P(i,m)的行程时间为到达停止线的时间与穿过交叉口的时间之和: 式(9)中:为从t=0 开始到车队P(i,m)通过交叉口的行程时间;其他变量意义同前。 所有车队通过交叉口的行程时间总和为: 式(10)中:T为所有车队通过交叉口的总行程时间;ψ为所有车队所在的集合;ψ1为需停车等待的车队集合;ψ2为可直接通过交叉口的车队集合;其他变量意义同前。 结合式(7)与式(11),有: 综上,可得所有车辆行程时间的计算公式: 1.4.2 优化模型的约束条件 (1)车辆行驶时间约束 ICC 可通过对CAV 进行控制使其以一定的速度行驶,并对CV 给予速度建议,若需要加减速,则控制车队P(i,m)以恒定的加速度或减速度通行。车队P(i,m) 到达停止线时速度大于等于0,即: 式(14)中:为车队P(i,m)到达停止线时的速度。 车队抵达停止线需要的最长时间,即其减速直到在交叉口停止线停止的时间为: 式(15)中:di,m为车队P(i,m)到停止线的距离;其他变量意义同前。 车队P(i,m)抵达停止线的最短时间为: 式(16)中:为车队抵达停止线的最短时间;其他变量定义同前。 于是,车队P(i,m)抵达停止线的时间应满足以下条件: (2)绿灯开始时间约束 理想情况下,车队P(i,m)到达停止线的时间等于绿灯开始时间,即: (3)最小绿灯时间 为保证车队中所有车辆在一个相位内通过交叉口,对最短绿灯时间进行约束,即: 式(19)考虑CV 的存在,对绿灯的持续时间作了一定时间c的延长(取3s)。 (4)避免冲突约束 考虑到安全性,模型设置避免冲突约束以确保车队之间不发生碰撞: 式(20) 中: Ωi,m,i′,m′表示两个相冲突的车队P(i,m)和P(i′,m′)的信号相位顺序,为0-1 变量,Ωi,m,i′,m′=0表示P(i′,m′)的绿灯开始时间在P(i,m)的绿灯结束之后,Ωi,m,i′,m′=1 表示P(i′,m′)的绿灯开始时间在P(i,m)的绿灯结束之前;Ωi′,m′,i,m表示两个相冲突的车队P(i′,m′)和P(i,m)的信号相位顺序,意义同Ωi,m,i′,m′;M为1个无穷大的数。 ICC 根据优化的交叉口信号配时,计算车队如何抵达路口,并将方案发给车队中每个CV(如果存在)。目标是将车队(车辆)引导至期望状态(期望到达停车线的时间和期望速度vd)。 本文采用Stebbins 等[15]提出的考虑绿灯时间的车速优化引导策略(Green Light Optimal Speed Advisory,GLOSA)对车队进行引导。车队先以恒定的加速度或减速度加减速,然后匀速行驶,再以恒定的加速度或减速度达到期望状态。车队初始速度为vi,m,若有足够的时间以预期速度抵达停止线,如图3 所示,按照车队预期行驶距离ds与到停车线的距离di,m的大小关系将车队引导策略分为3种情况: (1)当ds=di,m时,车辆能直接加速或减速到期望速度,再匀速抵达停止线,如图3(a)所示; (2)当ds (3)当ds>di,m时,速度偏大,车辆需减速行驶,如图3(c)所示。 图3 引导策略(具有充足时间) 若车队没有足够的时间以预期的速度抵达停止线,如图4所示,按照ds与di,m的大小关系将对车队的引导策略分为两种情况: (1)当ds>di,m时,表明速度偏大,车辆需减速,使抵达速度低于期望速度,如图4(a)所示; (2)当ds 图4 引导策略(没有充足时间) 本研究采用由德国宇航中心(Deutsches Zentrum für Luft-und Raumfahrt,DLR)运输系统研究所与科隆应用信息中心开发的中微观多模式交通仿真软件(Simulation of Urban Mobility,SU⁃MO)来搭建仿真环境。首先,利用SUMO路网文件搭建十字交叉口,运行车流文件生成车辆;然后,在Python 中通过调用traci 模块来获取车辆信息,得到信息后调用Gurobi 优化器求解1.4 节中的信号灯控制优化模型,并进一步通过1.5 节中的车队引导策略对车队进行轨迹引导;最后,在仿真过程中通过traci 模块提取每辆车的停车次数、延误、能耗等信息,并利用得到的数据进行结果分析。 本文所建信号灯控制优化模型是一种二元混合整数线性规划(Binary Mixed Integer Linear Pro⁃gramming,BMILP)模型,采用分支定界算法求解。模型的输入变量为ni,m,vi,m,di,m;决策变量为Si,m;目标函数为minT。模型共有7 个约束(式(14)~式(21))、16个整数变量、32个二进制变量和8 个连续变量。因此,可以实现实时性求解优化模型(CPU 为Inter Core i7-7700HQ 的普通笔记本电脑可在20ms 内求出结果,满足实时性要求)。 自适应交通控制是智能交通系统的一部分,在欧美国家已得到广泛应用,可以根据交通流的变化而实时调整信号配时,相比于传统信号控制在缓解交通拥堵、降低延误及能耗等方面表现良好,具有很好的可比性,被广泛用作信号控制优化对比方案。因此,下面将本文提出的模型与同等环境下自适应交通控制方案进行比较。 2.2.1 不同进口道流量下结果对比 本文设置两种交通流量(100veh·h-1·lane-1和400veh·h-1·lane-1),交叉口如图1 所示,左/直/右交通流的转向比为1∶1∶1,设置5%~100%的CAV渗透率,运行仿真系统3 600s,对比本文提出的模型和自适应交通控制方案(见表1),得到平均停车次数、平均延误、平均能耗曲线如图5~图6所示。 表1 不同条件下本模型相比自适应交通控制方案优化效果 图5 进口道流量100veh·h-1·lane-1仿真结果 图6 进口道流量400veh·h-1·lane-1仿真结果 由以上仿真结果可以看出,本模型的平均停车次数接近0,远低于自适应配时方案,在不同自动驾驶车辆渗透率和不同流量下,本模型平均停车次数降低90%左右;对于平均延误,随着CAV 渗透率的提高,本模型相比自适应配时方案可降低20%~30%;在能耗方面,随着CAV 渗透率的提高,本模型能耗降低显著,可达10%~15%。以上结果表明,本模型在不同CAV 渗透率下皆有较好的优化效果。 2.2.2 不同组队接受概率下指标优化结果 为了验证CV 速度建议接受概率对于交通运行效率的影响,本文在交通流量为400veh/h 的情况下,对比了4种CV接受速度建议概率(95%,90%,75%,50%)下,本模型的交通运行效率指标(平均停车次数、平均延误、平均能耗)相对自适应控制方案的优化效果,结果如表2~表4所示。 表2 不同组队建议接受概率下平均停车次数优化 表3 不同组队建议接受概率下平均延误优化 表4 不同组队建议接受概率下平均能耗优化 由表2~表4可知: (1)本模型对于平均停车次数减少具有很好的优化效果,在不同渗透率和CV 速度建议接受概率下,优化效果大于80%; (2)CAV 低渗透率的情况下,组队建议接受概率对平均延误和平均能耗的影响较大,随着CAV渗透率的增加,影响在逐渐减弱; (3)CAV 渗透率高于40%时,平均能耗和平均延误均具有一致的优化效果。当渗透率为40%时,平均能耗的优化效果分别为:6.71%,6.27%,5.42%和6.15%,即无论CV 是否听从组队建议,本模型都有一致的优化效果。 综合不同组队建议接受概率下的模型仿真结果可知,在较高CAV 渗透率时(高于60%),CAV 对CV 的行驶轨迹会有较好的引导作用,削弱了CV 未接受组队建议造成的影响;当CAV 渗透率较低时,CV 作为头车的概率更大,引导作用减弱,在停车线等待的情况增多,在极低CAV渗透率(5%)下,CV 接受速度建议的概率对模型表现有较大影响,当速度建议接受概率为50%和75%时,本模型提出的方法仅在停车次数上具有较好的优化效果。 本文针对CAV 和CV 混行的情况,构建了交叉口混行车队通行的信号优化和轨迹引导模型,以解决在不同CAV 渗透率条件下的交叉口通行权分配问题。通过微观交通仿真对所建模型进行验证,发现该模型可以有效减少延误和停车次数、降低能耗。最后,进一步探讨了人工驾驶车辆速度建议接受概率对交叉口运行效率的影响。所建模型及其结果可为未来智能网联环境下混行交叉口控制提供参考。不过,本文仅考虑了单交叉口的控制优化,后续将对多个交叉口路网的协调控制优化展开进一步研究。
1.4 信号灯控制模型优化

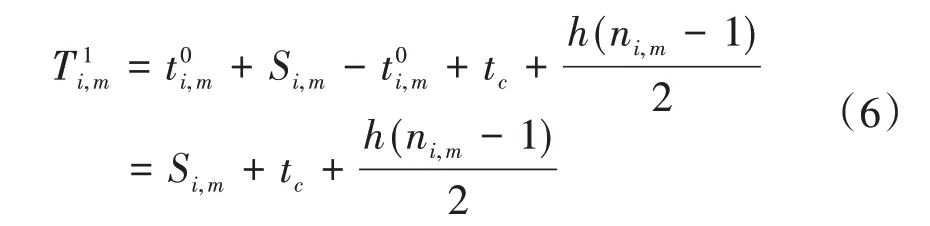

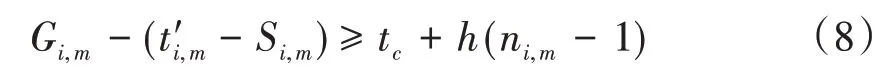

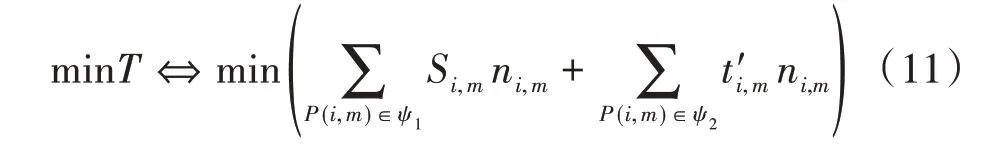

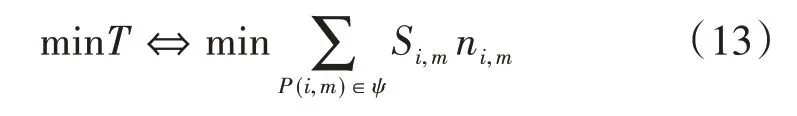
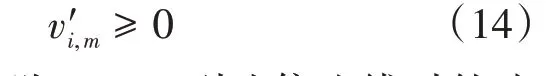

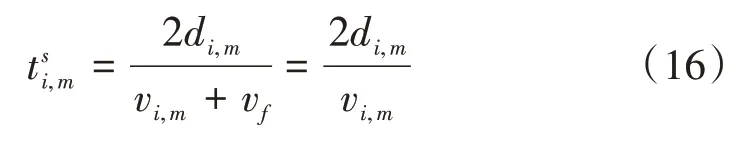


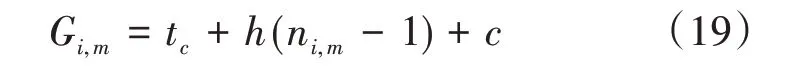
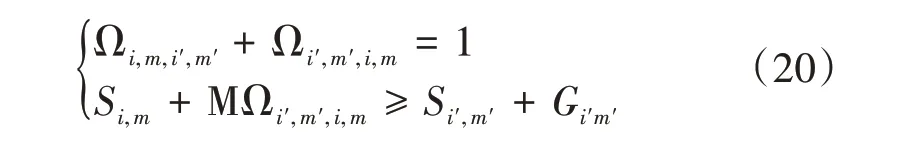
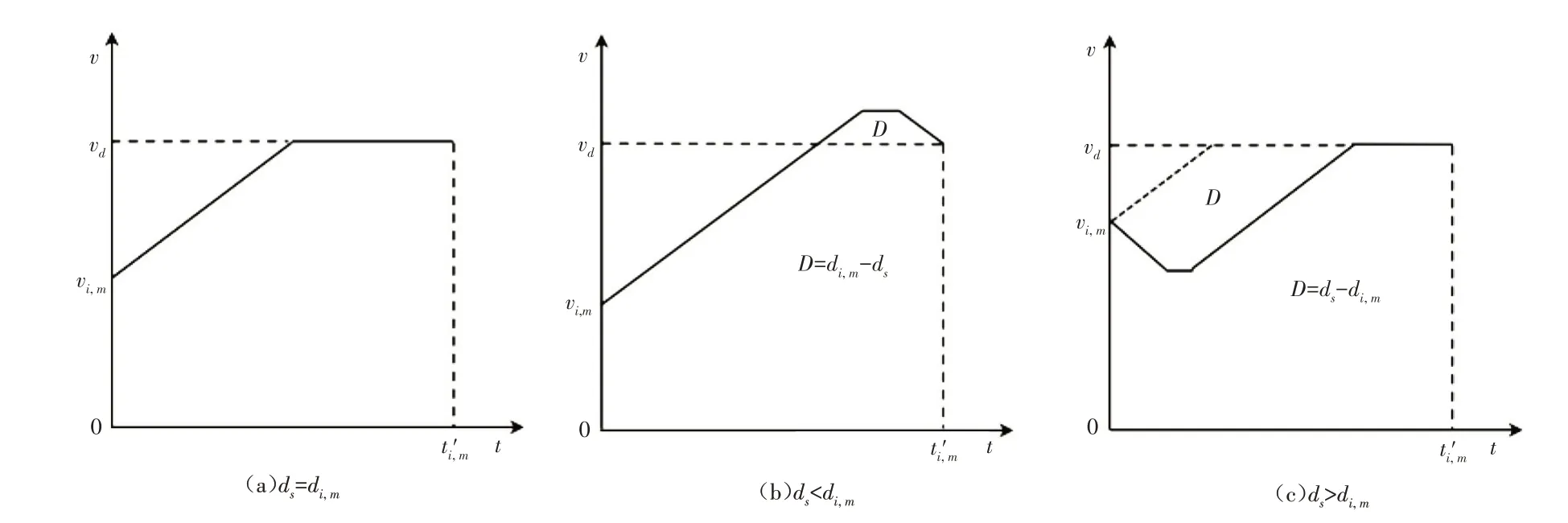
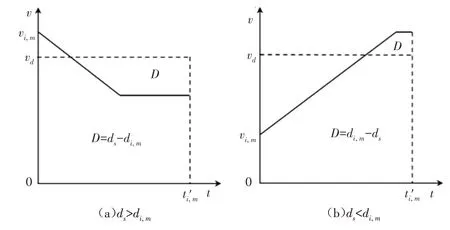
1.5 车队(车辆)实时引导策略
2 模型求解与分析
2.1 仿真平台
2.2 模型求解及分析

3 结语
