软土地层地铁盾构隧道结构病害数值模拟及分析

2021-01-18李庆桐

铁道标准设计 2021年1期

李庆桐

(上海申通地铁集团有限公司,上海 201103)

引言

从1969年首都北京开通中国大陆的第一条地铁开始，中国城市轨道交通已经走过50年的发展历程，特别是近10年以来，其建设规模和建设速度举世瞩目[1]。以交通流量大、建筑物密集的长江经济带上的龙头城市——上海为例，2/3的地铁区间隧道为盾构隧道。由于软土地层具有变形量大、承载力低的特性，使得呈一维地下管状结构的隧道衬砌发生纵向不均匀沉降，导致盾构隧道在服役过程中存在不同程度的结构病害，其中裂缝与渗漏水是最常见的两种病害[2]。

近年来，随着计算机、数码相机、存储器、图形处理器(Graphics Processing Unit，简称GPU)、人工智能算法等软硬件的快速发展，国内外已有学者[3-5]将计算机视觉和深度学习应用到盾构隧道结构病害的图像识别之中，并能够快速精准地提取病害的详细参数，如裂缝长度和宽度、渗漏水面积等。就隧道维护保障部门而言，仅仅将结构病害的区域从数字图像中识别或者提取出来，并不能从根本上解决实际中的工程问题。上海市工程建设规范DG/TJ08—2213—2013《盾构法隧道结构服役性能鉴定规范》[6]的条文说明中第3.1.2条指出，隧道检查的目的是对隧道结构服役性能做出评价。盾构隧道衬砌上裂缝、渗漏水等结构病害的严重程度直接关系到衬砌结构服役性能的高与低[7]。然而，结构病害参数与结构服役性能之间的这种力学关系尚不清晰，直接制约了病害严重程度的客观评价。文献[8]指出目前运营地铁盾构隧道的渗漏水危害等级评价具有模糊性、不确定性的问题。

为了解决以上不足，通过有限元模型(Finite Element Model，简称FEM)的数值模拟手段，来研究裂缝和渗漏水病害共同存在的情况下衬砌结构服役性能的变化规律。

1 盾构隧道三维实体模型

在隧道工程的结构分析中，由于岩土体本构关系的非线性、荷载及边界条件的复杂性，采用解析方法求解的难度较大，通常需要采用数值方法进行计算。与ANSYS、ADINA等大型通用有限元软件相比，ABAQUS包含十分丰富的材料模型、单元模式、荷载及边界条件，尤其在求解非线性问题方面具有独特优势，对隧道工程有较好的适用性。本文采用ABAQUS软件开展建模工作。

图1 接头弱化模型的示意(单位：mm)

对于已运营的地铁盾构隧道，其埋深和周围土体的性质会对隧道结构内力产生重要影响，而且需要对渗漏水病害进行仿真模拟，所以采用地层结构法建立模型。根据对盾构隧道管片接头处理方法的不同，管片计算模型主要有匀质圆环模型、等效刚度圆环模型、自由铰圆环模型、接头弱化模型[9]、梁-弹簧连续模型[10]、梁-接头不连续模型[11]、壳-接头模型[12]等。在以上这些模型中，弹簧或铰接的非连续模型难以考虑渗漏水病害的数值模拟，匀质或等效刚度的圆环模型得到计算结果偏保守，接头弱化模型的计算结果相对较接近真实的隧道变形和内力情况[13]。因此，本文研究采用接头弱化模型，如图1所示。按照上海地铁盾构隧道的防水设计要求，接头宽度取5 mm；根据横向刚度有效率η=0.67[14]拟合出的接头模量E′=500 MPa。

以上海城市轨道交通中的地铁盾构隧道为模型背景，该盾构隧道的衬砌外径为6.2 m，衬砌内径为5.5 m，管片厚度为0.35 m，通缝拼装，管片宽度为1.2 m，混凝土强度等级为C55，其弹性模量为3.55×104MPa，泊松比为0.15。对于隧道周围土层，以隧道衬砌圆心为基准，其隧道顶部上覆土层表面距圆心距离为18.1 m，底部土层下表面距圆心距离为34.1 m，土层总厚度为52.2 m；水平两侧土层边界距圆心距离各为34.1 m，土层总长度为68.2 m。可以看出，盾构隧道衬砌外表面距下部、左侧、右侧土层边界的距离均取5倍的衬砌外径(6.2 m×5=31 m)。表1给出了土层的物理力学参数。盾构隧道衬砌结构及其土层的分布示意如图2所示。考虑到该盾构隧道所处的地区为软土富水区，假设地下水位线与地表面持平。

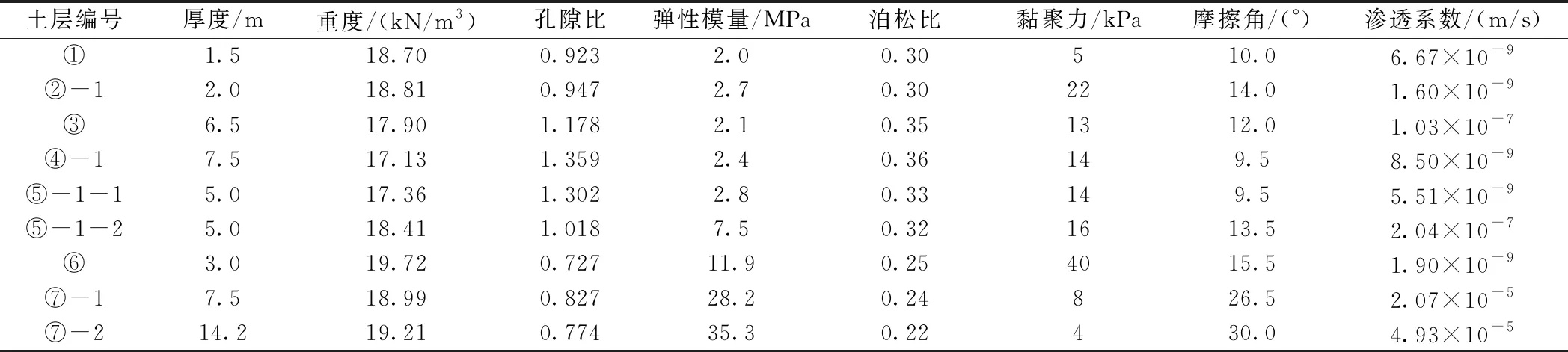
表1 土层的物理力学参数

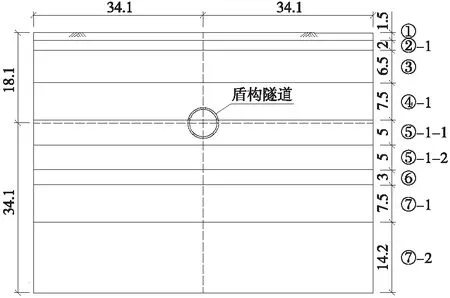
图2 土层分布与隧道位置示意(单位：m)

土层本构模型采用摩尔库伦(Mohr-Coulomb)模型，其参数取值依据表1确定。混凝土本构模型采用Saenz公式简化后的双折线线性强化弹塑性模型[15]，如图3所示。对于强度等级为C55的混凝土而言，其物理力学参数如表2所示。

图3 混凝土应力应变曲线

表2 管片混凝土的物理力学参数

模型的顶部表面不设置约束，底面设置固定约束，左右两个侧面设置水平约束，保持竖向位移自由。假设管片拼装完成之后，衬砌结构与土体之间不发生相对滑移，始终保持接触状态，因此，衬砌结构与土体之间的接触面采用绑定约束。对土体划分网格时采用ABAQUS内部的渗流计算单元，其满足渗流与固结沉降的耦合分析要求[16]。

考虑到计算机的运算能力，本文研究沿纵向取3个衬砌管片来建立上述盾构隧道的三维实体有限元模型，如图4所示。管片与管片之间的环缝也采用宽度为5 mm、模量为500 MPa的接头弱化模型来考虑。环缝与管片之间采用绑定约束。该模型共有20 739个单元。分析步主要包括：(1)地应力平衡；(2)土体开挖及衬砌激活；(3)超载施加(最大超载设置为180 kN/m2)；(4)长期渗流固结。

图4 基于地层结构法的盾构隧道三维实体模型(单位：m)

2 结构病害模拟方法

根据地铁盾构隧道的病害检测结果，裂缝与渗漏水两种结构病害往往同时存在，并相互影响。裂缝病害发生在混凝土管片的表面；渗漏水病害常发生在管片与管片的拼缝之间。渗漏水病害会导致衬砌结构外荷载发生变化，使衬砌结构的椭圆化变形增加，引起裂缝病害的扩展，而裂缝病害的进一步扩展又会导致衬砌结构刚度下降，管片拼缝进一步张开，渗漏水量相应地增加，持续恶化隧道结构及其受力状态，从而威胁盾构隧道的安全运营。因此，本文研究是基于盾构隧道三维实体模型，对裂缝和渗漏水两种结构病害进行同时模拟分析。

2.1 裂缝病害

对于混凝土结构中的裂缝病害，其力学模型主要有3种：(1)分离式裂缝模型(Discrete Crack Model)[17-18]；(2)分布式裂缝模型(Smeared Crack Model)[19]；(3)内嵌式裂缝模型(Embedded Crack Model)[20]。分离式裂缝模型是最早模拟混凝土开裂的模型，其基本思路是将裂缝设置为单元边界，一旦出现裂缝就及时调整节点位置或增加新的节点，并重新划分单元网格，使裂缝处于单元边界与边界之间。分布式裂缝模型假定裂缝在单元内部形成，当单元达到开裂条件后，就在垂直于主拉应力的方向产生裂缝。内嵌式裂缝模型是通过改造单元形函数的方式来构造内嵌裂缝的特殊单元模型。由于分离式裂缝模型能够较好地描述裂缝病害引起的非连续性，方便设置裂缝病害的位置、形状、宽度、长度等参数，而且在本文研究中不考虑裂缝病害的扩展演化，所以选择分离式裂缝模型对盾构隧道衬砌结构中的裂缝病害进行有限元模拟。

分离式裂缝模型又可分为张开型、滑开型、撕开型3种裂缝类型，如图5所示[21]。其中，张开型裂缝是由于受拉破坏引起，其裂缝表面位移上下相反，方向垂直于裂缝扩展方向；滑开型裂缝是由于剪切破坏引起，其裂缝表面位移前后相反，方向平行于裂缝扩展方向；撕开型裂缝是由于拉剪破坏引起，其裂缝表面位移左右相反，方向平行于裂缝扩展方向。

图5 裂缝扩展的基本类型(u指裂缝扩展产生的位移)

根据盾构隧道结构病害检测的统计结果，发现衬砌管片顶部内侧出现裂缝病害的概率较高，也更加容易扩展演化，而且裂缝病害的起点位置大都从拼缝处开始。文献[13]通过室内模型试验和数值模拟，进一步验证了对隧道结构安全性能威胁最大的裂缝区域是衬砌管片顶部内侧受拉区域。因此，为了取得较为明显的数值模拟效果，研究通过预留裂缝的方式在管片顶部内侧的最不利区域内模拟张开型的裂缝病害。图6给出了盾构隧道三维实体模型中的裂缝病害模拟，其长度和宽度根据计算工况确定，深度参考文献[13]的双直线模型确定。盾构隧道管片裂缝病害的双直线模型是通过裂缝宽度来计算裂缝深度的一个实用的简化计算模型，是依托TJGPJ-2000管片加载系统，对足尺的地铁盾构隧道管片进行四点弯正弯矩试验而建立的。该双直线模型如图7所示，其计算式见式(1)。

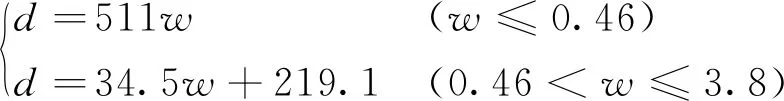
(1)

式中，w为裂缝宽度，mm；d为裂缝深度，mm。

图6 盾构隧道三维实体模型中的裂缝病害模拟

图7 盾构隧道管片裂缝病害的双直线模型

2.2 渗漏水病害

在盾构隧道的服役过程中，虽然衬砌管片的接头、螺栓孔、注浆孔等位置采用了特殊的材料及构造防水措施，但由于隧道变形、材料老化等不利因素的影响，难以避免防水措施的失效，进而引发渗漏水病害。盾构隧道衬砌出现渗水病害后，土层中水分会发生流失现象，导致土体中孔隙水压力降低、有效应力增加，使得土体发生重新固结，影响隧道衬砌结构受力状态。针对渗漏水病害在衬砌表面的分布位置，文献[22]通过现场调查和统计分析发现：接头渗漏水占88.17%，注浆孔渗漏水占8.77%，螺栓孔渗漏水占3.06%，具体如图8所示。可以看出，接头渗漏水所占的比例非常高，注浆孔渗漏水和螺栓孔渗漏水所占的比例较低。因此，研究仅考虑接头渗漏水病害，包括环缝渗漏水、纵缝渗漏水、十字缝渗漏水3种类型。

图8 渗漏水病害在衬砌表面的分布规律

对于隧道衬砌渗漏水病害的数值模拟方法，主要分为3类：均质渗漏模型、差异渗漏模型和局部渗漏模型。均质渗漏模型是将隧道衬砌整体等效成为均质渗流，如泰国亚洲理工大学Arjnoi等[23]通过设置衬砌内部的渗透参数，对排水隧道出现渗漏水病害后土体孔隙水压力的分布规律进行了研究。差异渗漏模型是根据隧道衬砌的不同位置，有差异地设置不同的渗透系数，如英国岩土工程咨询集团Wongsaroj等[24]对伦敦地铁盾构隧道的长期沉降进行分析时，将管片的上部与下部分别设置不同的渗透系数，其模拟结果与检测数据的吻合度较好。局部渗漏模型是针对渗漏水病害可能出现的局部区域(如接头位置等)而设置渗流路径，其他位置不发生渗漏，如同济大学刘印等[25]采用该方法分析了盾构隧道长期渗漏下隧道周边孔隙水压力、地表沉降等的变化规律。以上3种不同的渗漏水病害模拟方法如图9所示。虽然盾构隧道的渗漏水病害大多发生在拼缝部位，但对于不同区间的盾构隧道而言，其渗漏水病害发生的部位相差较大。如果采用均质渗漏模型和差异渗漏模型的话，难以真实地模拟实际工程情况。因此，采用局部渗漏模型开展盾构隧道渗漏水病害的数值模拟。

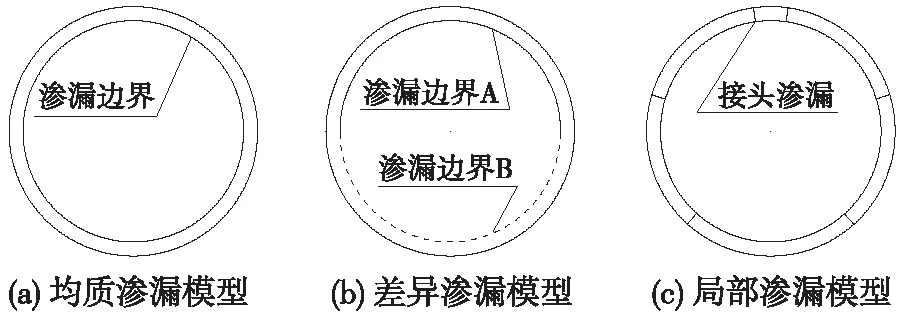
图9 隧道渗漏水病害的3种数值模拟方法

当渗漏水病害的发生位置与裂缝病害越接近时，由渗漏水引起的裂尖应力和裂缝宽度的增长值也越大[13]。为了便于分析结构病害对盾构隧道服役性能的影响，渗漏水病害的模拟位置设置在封顶块与邻接块的管片接头处。图10给出了盾构隧道三维实体模型中的渗漏水病害模拟。基于可以实现流固耦合分析的孔压单元(Pore Pressure Element)，在盾构隧道管片接头处设置渗漏水病害的渗流路径，其路径宽度与接头宽度相同(按照上海地铁盾构隧道的防水设计要求取5 mm)，路径长度取150 mm，再设置相应渗流单元的属性及渗透系数，即可模拟管片接头处的渗漏水病害。根据上文中关于地下水位线位于地表的假定，将地表孔压设置为0。为了保证渗流的连续性，衬砌管片单元类型选择孔压单元。当衬砌管片发生渗漏水病害时，渗出侧位于管片内侧且与空气直接接触，故管片内侧孔压设置为0。管片单元与土体单元之间采用绑定约束，初始渗流场分析会自动计算管片外侧迎水面的孔压，不需要再专门进行设置。由于该盾构隧道三维实体模型的尺寸远大于隧道衬砌尺寸，认为土体两侧及底面的3个边界不会由于渗漏水病害而引起土层中水体的流动，故设置为不透水边界。

图10 盾构隧道三维实体模型中的渗漏水病害模拟

3 计算方案

盾构隧道衬砌表面上出现的裂缝病害通常不是直线形状，而是具有一定曲率变化的曲线形状。裂缝病害的主要量化参数有长度、宽度、深度、位置。由于本文采用图7所示的双直线模型，所以宽度和深度是一一对应的，因此仅考虑裂缝病害的宽度信息。鉴于裂缝病害出现的位置主要集中于管片顶部内侧，仅研究管片顶部内侧位置处的裂缝病害。

由GB 50208—2011《地下防水工程质量验收规范》[26]表C.1.5知，渗漏水病害主要有5种类型，分别是湿渍、渗水、水珠、滴漏、线漏。文献[27]对盾构隧道不同类型渗漏水病害的统计结果发现：渗水的比例为76%，湿迹的比例为17%，滴漏比例为7%，水珠的比例为0，线漏的比例为0。可以看出，滴漏的所占的比例较少，且滴漏的渗水量与其面积之间没有明显的相关性(面积很小可能渗水量很大)，所以本文研究暂不考虑滴漏这种类型的渗漏水病害。对于下述所提及的渗漏水病害，均是指渗水与湿迹两种类型。渗漏水病害的量化参数主要有面积和位置两种。对于渗漏水病害发生的位置主要是管片拼缝处，即环缝、纵缝、十字缝等3处。对于渗漏水病害的面积，其大小与渗漏量有关；而渗漏水病害在渗流通道面积和水力坡降一定的情况下，与渗透系数成正比关系，具体如式(2)所示。在数值模拟过程中，通过设置不同的渗透系数来描述渗漏水病害的不同面积。

q=kiA

(2)

式中，q为渗水量；k为渗透系数；i为水力坡降；A为渗漏通道面积。

为了便于裂缝和渗漏水病害数值模拟，假设盾构隧道衬砌表面上的裂缝病害均为直裂缝，渗漏水病害区域均为圆形。对于隧道衬砌结构，病害数量的增加会显著降低完整性，从而降低其服役性能[6]。就本文所要模拟的结构病害数量而言，在不影响计算精度前提下，出于对计算时间的考虑，在盾构隧道三维实体模型中仅考虑1处裂缝病害和1处渗漏水病害。因此，本文计算主要是针对裂缝宽度、长度和渗漏水面积、位置等4个量化参数开展研究。

各计算因素的水平选取如下：

(1)以实际裂缝病害的最大宽度为参考，选取数值模拟中裂缝病害的宽度为3个水平，分别为1，3，5 mm；

(2)以实际裂缝病害的长度为参考，选取数值模拟中裂缝病害的长度为3个水平，分别为50，100，150 mm；

(3)参考文献[13]，[27]对渗漏量分别为0.1，0.15，0.5，1.0 L/(m2·d)时所计算的渗透系数，将渗漏水病害的渗透系数设置为3水平，分别为1×10-6，5×10-6，9×10-6m/s；

(4)根据盾构隧道渗漏水病害经常发生的位置(环缝、纵缝、十字缝)，给出了渗漏水病害位置的3个水平，分别用H、Z、S三个字母进行指代，其中，H代表环缝渗漏水，Z代表纵缝渗漏水，S代表十字缝渗漏水，具体的数值模拟位置如图11所示。

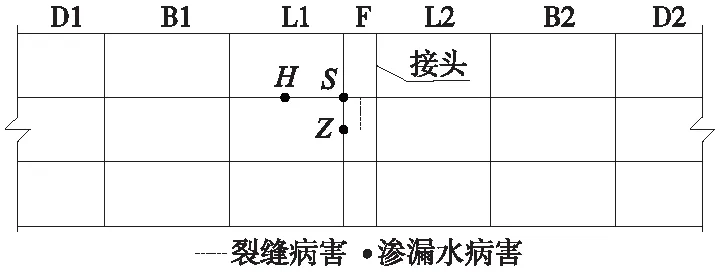
图11 裂缝和渗漏水病害的模拟位置示意(F为封顶块、L为邻接块、B为标准块、D为封底块)

需要特别说明的是，裂缝病害的模拟位置是设置在封顶块的内表面中心处，且裂缝病害的一端与环缝相接。之所以将裂缝病害的一端与环缝相接，是由于实际衬砌表面的裂缝病害大都是起始于管片拼缝，极少发现裂缝病害出现在衬砌表面的内部。这种特征与公路隧道衬砌上的裂缝病害相差较大。

表3列出了本文研究中各计算因素的水平。为了减少计算次数，优化计算结果，提高数据可靠性，采用标准正交表L9(34)设计计算工况。计算工况共有9个，具体如表4所示。

表3 计算因素水平

表4 计算工况

4 计算结果及其分析

根据确定的计算方案，采用ABAQUS有限元分析软件，实现不同工况下盾构隧道衬砌结构的应力计算。文献[13]在研究盾构隧道接头渗漏水对衬砌结构既有裂缝病害演化的研究中，采用裂尖应力作为计算指标，能够有效地评判隧道某一位置发生渗漏水病害时的最危险裂缝位置。为此，采用裂尖最大应力作为计算指标。裂尖最大应力是指隧道衬砌管片顶部内侧受拉区域中预留裂缝病害处的最大Mises应力值。在超载和长期渗流固结的作用下，裂缝病害处会发生一定程度的应力集中现象。根据数值模拟的计算结果发现，工况1～工况3尚未出现应力集中现象；工况4～工况9存在一定的应力集中现象。不同工况的裂尖最大应力计算结果如表5所示。不同计算工况下盾构隧道衬砌结构的Mises应力云图如图12所示。

图12 不同计算工况下衬砌结构Mises应力云图

表5 不同工况的裂尖最大应力

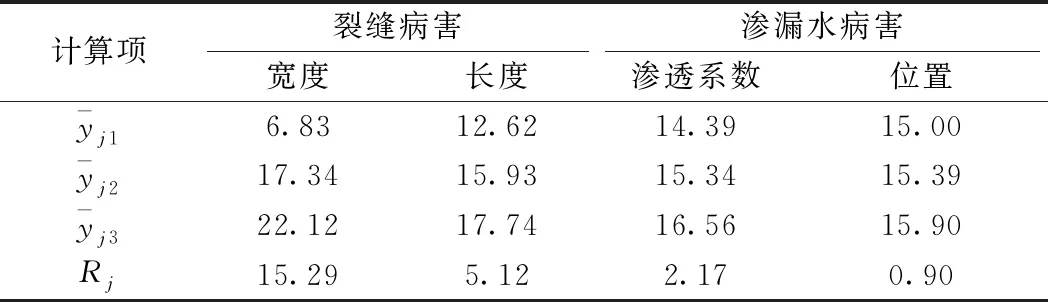
表6 极差分析法的计算结果 MPa

为了分析病害参数在不同水平下裂尖最大应力的变化规律，图13分别给出了不同病害参数水平下裂尖最大应力的变化曲线。随着裂缝宽度和长度、渗漏水的渗透系数等3个参数的单调增大，裂尖最大应力均呈现出单调增大的趋势。当渗漏水病害的位置依次取环缝、纵缝、十字缝时，裂尖最大应力也均呈现出单调增大的趋势。

经过以上计算分析，得到了裂缝宽度、长度与渗漏水病害的渗透系数、位置等4个参数的数值变化对隧道衬砌结构裂尖最大应力的影响规律，揭示了裂缝和渗漏水病害共同存在情况下衬砌结构服役性能的变化规律。

图13 不同病害参数水平下裂尖最大应力的变化曲线

5 讨论

图14给出了地铁盾构隧道衬砌表面实际的裂缝和渗漏水病害图像。从图14可以看出，裂缝病害大多发生在顶部管片边角处；渗漏水病害以腰部管片拼缝处发生渗流为主。

在荷载的作用下，盾构隧道衬砌结构普遍呈现出“横鸭蛋”式的变形(水平直径增大，竖向直径减小)。衬砌顶部区域的管片处于内侧受拉，腰部区域的管片处于外侧受拉。内侧受拉容易导致混凝土拉应力超过极限拉应力，致使管片上出现可被肉眼观测到的裂缝病害。在螺栓的约束下，虽然裂缝病害的长度不大，但通常会有较大的宽度，说明裂缝宽度是描述结构服役性能的一个主要参数。饱和软土地层中管片外侧受拉时，会导致管片接头处张开量增大，降低接头抗渗性能，从而引发渗漏水病害。渗漏量越大，隧道周围土体中孔压降低越快，使得土层有效应力增大，隧道外荷载显著增加，从而产生的裂尖最大应力也越大。以上分析与本文的研究结论相一致，一定程度上验证了结构病害数值模拟的有效性。