保积n元-Hom-李超代数的对偶表示
2021-01-18田丽军关宝玲
田丽军, 关宝玲
(1. 齐齐哈尔大学 通信学院, 黑龙江 齐齐哈尔 161006; 2. 齐齐哈尔大学 理学院, 黑龙江 齐齐哈尔 161006)
n-李超代数[1-2]是一类更广的结构, 包括n-李代数 (n元-Nambu-李代数)、n元-Nambu-李超代数和李超代数. 一般的Hom-代数结构与向量域上的拟形变和离散化有联系. 这些拟形变产生了拟李代数---- 一个斜对称性和Jacobi等式被扭的广义李代数结构. 文献[3-8]分别讨论了Hom-李代数、 Hom-李超代数、 Hom-李双代数、 Hom-李2-代数和拟Hom-李代数; 文献[9]介绍了n元-Hom-Nambu-李代数, 它是线性映射扭恒等式李型n元-代数的推广, 包括广义李型n元代数, 如n元-Nambu代数、n-ary-Nambu-李代数和n元-李代数[10-12]. 本文考虑保积n元-Hom-李超代数, 把保积n元-Hom-李代数的对偶表示推广到保积n元-Hom-李超代数的情形.
1 预备知识
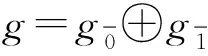
|[x1,…,xn]|=|x1|+…+|xn|,
(1)
[x1,…,xi,xi+1,…,xn]=-(-1)|xi||xi+1|[x1,…,xi+1,xi,…,xn],
(2)
其中|x|表示g中齐次元素x的2-次数, 则三元组称为n元-Hom-李超代数.
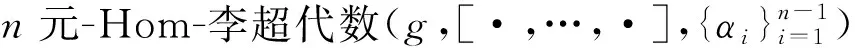
定义2[13]设(g,[·,…,·],α)是n元-Hom-李超代数,X=x1∧…∧xn-1∈∧n-1称为g的基本物体. 对所有的z∈g,X·z∶=[x1,…,xn-1,z], 显然有|X|=|x1|+…+|xn-1|. 设X=x1∧…∧xn-1和Y=y1∧…∧yn-1是g的基本物体. 一个双线性映射[·,·]α: ∧n-1×∧n-1→∧n-1定义如下:


(4)
ρ(X)·Vβ⊆Vβ+|X|, ∀β∈2,
(5)

(6)
则称ρ为V上g的阶化表示,2-阶化表示空间(V,ν)称为阶化g-模. 其中:表示其下的元省略.
2 主要结果
下面考虑保积n元-Hom-李超代数的对偶表示. 保积n元-Hom-李代数的对偶表示可参见文献[14]. 设(V,ρ,β)是保积n元-Hom-李超代数(g,[·,…,·]g,α)的表示, 其中β是可逆的, 即β∈GL(V). 定义ρ*: ∧n-1g→gl(V*)为
〈ρ*(X)(ξ),u〉=-(-1)|X||ξ|〈ξ,ρ(X)(u)〉, ∀X∈∧n-1g,u∈V,ξ∈V*.
(8)
定义ρ★: ∧n-1g→gl(V*)为
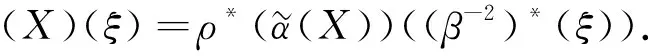
(9)
如果(V*,ρ★,(β-1)*)是(g,[·,…,·]g,α)的一个表示, 则称其为(V,ρ,β)的对偶表示.
定理1设(V,ρ,β)是保积n元-Hom-李超代数(g,[·,…,·]g,α)的表示, 其中β是可逆的. 则(V*,ρ★,(β-1)*)是g在V*上的对偶表示当且仅当下列条件成立:
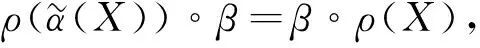
(10)
∀xi,yi∈g, 1≤i≤n-1,u∈V.
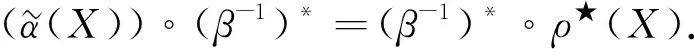
直接计算可得
因此有
即

通过计算可得
由式(10),(11), 有
又有
因此(V*,ρ★,(β-1)*)是保积n元-Hom-李超代数(g,[·,…,·]g,α)的一个表示.
必要性. 由于(V*,ρ★,(β-1)*)是g的表示, 根据定义有
由充分性的证明可知, 对∀xi,yi∈g, 1≤i≤n-1,u∈V, 有
比较式(12)和式(13)可得
证毕.
