浅析高中数学建模思想培养策略
2021-01-17王钰琦
王钰琦
【摘要】随着社会的变化,人们对数学和人才培养质量也不断提出新的要求。加之新的教育理念、教育方法、教育技术快速地涌进一线教学,数学建模的教学也处在不断地变化甚至是挑战之中。本文立足于高中数学教学角度,分析了高中数学建模思想培养策略,希望具有一定参考价值。
【关键词】高中数学;建模思想;课堂教学
引言:随着不断的变化和认识,数学建模已经不再是陌生的事物。由于数学建模可以简化数学问题,更容易地分析数学数据解决数学问题。近年来,数学建模教学在我国中学教学中得到了广泛的应用。许多从事数学教学的积极参与到数学建模教学领域的研究中,寻找答案来解决数学教学中存在的问题。
一、选取内容,渗透模型
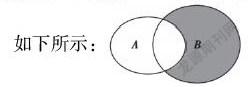
建模思想,是学生所应掌握的重要思想,能使他们更好地应用数学模型解决实际问题。日常教学中,为了向学生渗透建模思想,要精心筛选适合的教学内容。在教学内容选取中,为了保证每一位学生都能养成良好建模能力,要根据他们的接受能力,选择相对基础的内容,用基础性内容帮助学生顺利理解数学模型。同时,要精心筛选适合学生心理、年龄和认知水平的教学内容,以奠定好他们学习数学建模的基础,为他们营造一个良好的模型建立体验环境。另外,在对教学内容进行筛选时,要尽量选取趣味十足的内容,以唤醒他们建模兴趣,使他们具备良好的建模思想。如在《集合的基本运算》一课教学时,可精心选取“并集”这一基础性教学内容向学生渗透建模思想。在“并集”基础性知识教学中,先请学生类比实数的加法运算,对集合“相加”进行分析,说一说A={1,3,5},B={2,4,6},C={1,2,3,4,5,6}中集合C与集合A、集合B之间的关系。经过一段时间的观察、类比、思考,学生们将初步总结出并集概念。接着,可为学生完整补充出A∪B并集概念,引出A∪B={x|x∈A,或x∈B}这个并集模型,并用Venn图表示公式。
如下所示:
待学生掌握了并集概念以后,请他们自主建立模型,用并集运算符号表示上述A、B、C之间的关系。随即,学生们将建构出A∪B=C这样一个数学模型。在这里,通过选取基础性教学内容,让学生对建模思想有了初步认识。上述教学活动,考虑到学生们已经掌握了实数加法运算,在“并集”这一基础性内容教学中,层层递进,有目的地向学生渗透了集合“相加”数学模型构建思想,为他们布置了一个自主构建并集模型的任务,使他们在教材内容学习中深刻认识到了数学模型构建重要性,初步形成了建模思想,学会了通过类比、观察、思考等活动构建模型。
二、组织活动,巩固模型
活动的组织,利于巩固学生对数学模型的掌握。实际教学中,要根据具体的教学内容,组织形式多样、丰富多彩的数学活动,丰富学生数学建模体验。在数学活动具体组织过程中,要保证活动内容新颖,有一定智力价值。如此,能更好地实现对学生建模思想的培养。同时,在数学活动组织中,要充分考虑学生们的兴趣点,要突出实践性,以保证学生通过洞察与探究数学模型实现建模思想良性发展。课后,是巩固学生数学模型应用的有利时机。因而,在《指数函数》一课教学时,为了加深学生对指数函数模型这样一个数学模型的理解。课后,可组织一次实践动手操作活动。活动中,向学生提出这样一个问题:某种放射性物质不断变化为其他物质,每经过1年,剩留的这种物质是原来的84%,大约经过几年剩留量是原来的一半?问题驱动下,鼓励学生先建立一个物质剩留量关于经过年数的函数模型,再尝试动手绘制图象,通过观察图象得出正确结论。在这个过程中,学生们将运用自身已掌握的课堂知识,在设该物质最初量为1的基础上,假设经过x年还剩y,由此推导出经过1年,y=1×84%=0.84。经过第2年,y=0.84×84%=0.842。经过x年,y=0.84x(x>0)。接着,作出函数图象。结合图象,观察到y=0.5时,x≈4,最终得出经过4年物质剩留量是原来的一半。在这里,通过组织实际动手操作活动,引导学生建立指数函数模型,绘制指数函数图象,观察图象,增进了他们对指数函数模型的了解。同时,上述教学活动,为巩固学生日常学习中对数学模型的应用,结合“指数函数”知识教学内容,为学生搭建了一个良好的实际操作平台,鼓励他们自主动手构建指数函数模型,根据自身已掌握的知识,画出指数函数图象模型,并对图象模型展开多角度观察,认真提取图象模型中关键信息,最终应用模型解答出具体问题答案。
三、拉近距离,培养建模思想
例如,在“统计”这章内容的教学中,为了更好地培养学生对数学知识的应用能力,教师可以通过为他們布置实践作业的形式来更好地增强他们的数学学习体验。例如,教师可以创设生活情境:“请同学们在课下调查你所在小区居民的养狗情况,可以根据自身的实际情况进行调查,并以统计图的形式呈现,得出自己的结论。”如此一来,学生在应用知识的过程中也能逐步加深对知识的了解,从而激发学习兴趣。在此过程中,学生通过调查、分析、计算和建模这几个步骤,能够领悟建模思想在数学学习中的应用价值,从而有效培养自身对建模思想的实际应用能力。
结论:综上可知,基于核心素养导向下,要重视对学生建模思想进行培养。建模思想具体培养中,要用心筛选适合的模型思想渗透内容。同时,要重视创设适合的教学情境,并引导学生合作探究如何建构模型,与他们一起分析模型的构建问题,组织好数学模型应用活动,使学生真正养成良好数学建模思想,提高学科核心素养。
参考文献:
[1]林毅,周莹.新旧高中数学课标中必修课难度的定量比较研究[J].教学与管理,2020(30):26-28.
[2]何荣发,蒲锦泉.高中数学建模的实践与思考——以“饮料罐的优化设计”为例[J].福建中学数学,2020(10):42-45.
