复杂水力条件下平原区河系洪水预报模型应用探讨

陈瑜彬 香天元

摘要：针对平原区河系水力条件复杂，传统水文水力学模型建模资料需求高、流程复杂、模拟效果欠佳等问题，将平原区河系虚拟为一个水库模型，提出新安江模型、分段馬斯京根模型与水库调洪演算模型相耦合的平原区河系实用洪水预报模型。选取滁河流域晓桥站为研究对象，采用2010～2020年洪水样本对模型进行率定与检验，并以2020年大洪水为例开展应用探讨。结果表明：该洪水预报模型资料局限性低、建模过程简易，能较好地模拟平原区河系的水位过程，可为平原区河系水文预报提供参考。

关 键 词：洪水预报模型; 平原区河系; 滁河流域; 2020年大洪水

中图法分类号： TV697.3

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.12.004

0 引 言

河道水位是平原区洪水防御的重要技术指标。然而平原区河系通常存在水系纵横交错、水力条件复杂，水流上承汇流作用、下受回水顶托影响，水位预报难度较大[1-2]，因此，开展平原区河系水位预报意义重大。平原区河道水位预报普遍面临两方面难题：① 在暴雨洪水期间，因下游回水顶托影响，实际行洪能力被严重制约，行洪速度缓慢、水位被迫抬升、涨水历时长，峰现时间明显滞后，呈现显著的雨洪不对应[3]，这对传统洪水预报模型的适用性形成了巨大挑战;② 平原区大多资料条件有限[4]，除了相对充足的降水资料，水文资料多以水位观测资料为主，流量资料仅有部分巡测记录，此外沿程河道大断面资料也存在较大局限性，这严重制约了洪水预报模型的构建及应用。因此，在有限资料条件下，构建一个具有普适性的实用洪水预报模型，解决复杂水力条件下平原区河系的洪水预报问题，成为水文从业人员亟需解决的技术问题。

目前，国内外许多学者围绕复杂水力条件下平原区河系洪水预报问题开展了大量的研究，提出了许多新模型新方法，大体可归为两类：① 基于统计学范畴的经验模型[5-6]，其代表模型有P～HM相关图模型、P+Pa～HM相关图模型等，此类模型对资料要求较低，建模简单，能快速预报洪峰水位，但通常精度较低、不确定性较大，难以准确预报水位过程和峰现时间;② 具有相对明确物理参数的机理模型[7-8]，其代表模型有水力学模型、水文与水力学耦合模型等，此类模型通常能较好地模拟洪水发展过程，预报精度相对较高，但此类模型对资料条件要求高，建模复杂，对资料条件受限的区域实用性不强。因此，本文针对资料局限、建模复杂、精度不高、过程模拟不全等问题，提出了耦合新安江模型、分段马斯京根模型与水库调洪演算模型的平原区河系实用洪水预报模型，选取滁河流域晓桥站为研究对象，采用2010～2020年洪水样本对模型进行率定与检验，并以2020年大洪水为例开展应用探讨，以期为复杂水力条件下的平原区洪水预报提供参考。

1 平原区河系实用洪水预报模型构建

平原区河系存在河道比降小，槽蓄能力大，出口控制断面流量受上游径流汇入及下游回水顶托共同影响等特征，其规律表现在：当上游及区间来水（入流）大于出口断面流量（出流）时，断面水位上涨;反之，当上游及区间来水小于断面流量时，断面水位下降，断面水位的涨落与上游及区间来水存在直接关系。因此，根据入流、出流以及出口断面水位的关系，本文将平原区河系虚拟为有一定调节能力的水库（以下简称为“虚拟水库”），采用新安江模型计算集水面积内降雨径流（即区间来水），叠加采用分段马斯京根模型演算至出口断面的上游来水，得到水库入流过程，并采用水库调洪演算模型计算出口断面水位及出流过程，形成耦合新安江模型、分段马斯京根模型与水库调洪演算模型[6]的平原区河系实用洪水预报模型，模型结构如图1所示。

平原区河系实用洪水预报模型的应用关键在于模型参数的拟定，其中水库调洪演算模型的基础是联解水量平衡方程与蓄泄关系，需拟定出口断面水位流量关系线（即虚拟水库的泄流曲线）和槽蓄曲线（即虚拟水库的库容曲线）。考虑平原区资料条件，需严格按照泄流曲线拟定、新安江模型与分段马斯京根模型参数率定、库容曲线拟定的次序构建模型。

1.1 泄流曲线拟定

根据出口断面的资料情况，可选用多项式最小二乘法拟定[9]或经验公式计算[10]两种方法。

（1） 多项式最小二乘法拟定。有水位观测资料及实测流量记录的，采用多项式最小二乘法拟定泄流曲线（即断面水位流量关系线），其多项式拟合公式为

yi=a0+a1（xi-x-）+a2（xi-x-）2+…+

am（xi-x-）m（1）

式中：xi为水位观测值，yi为流量测量值，i=1，2，3，…，n;x-为xi的平均数;m为拟合多项式的项数，要求m≤n且m≤20，一般m取2或3。

（2） 经验公式计算。有水位观测资料及断面几何形状参数的，采用谢才-曼宁公式计算流量，其计算公式为

Q=ω·1nR16R·J（2）

式中：ω为过水断面面积;n为糙率，对于天然河道取值为0.020～0.200;R为水力半径;J为水力梯度。

对闸门控制的断面宜采用水闸过流计算公式，文献[11-12]有介绍，在此不再赘述。

1.2 新安江模型与分段马斯京根模型参数率定

虚拟水库的入流过程为上游来水与区间降雨径流所形成的合成流量，可采用新安江模型与分段马斯京根模型计算获得，也可依据库容曲线采用水量平衡计算获得，前者多用于计算预报入库，后者多用于推算实况入库。平原区河系的水文资料以水位、雨量为主，在虚拟水库的库容曲线拟定前，难以获得虚拟水库的实况入库资料。因此，在率定新安江模型与分段马斯京根模型参数时，应以水位过程为参照对象，通过POA等优化算法[13]，对去量纲的模拟入流INQi与实测水位Hi的时序序列进行比对，以两者的纳什系数最大值max{NSE}为优化求解目标，其相应参数则为最优参数，基于该参数，可使得模拟入流过程的起涨时间与实测水位过程的起涨时间基本一致。

1.3 库容曲线拟定

虚拟水库的库容曲线拟定是平原区河系实用洪水预报模型构建的重点，也是难点，采用试错法拟定，主要计算步骤如下（假定计算时段长为DT，单位为h）：

（1） 选择出口断面次洪持续上涨过程为样本。

（2） 依据拟定的泄流曲线，采用线性插值的方法以水位查算流量，得到出流过程（OTQi）。

（3） 采用新安江模型与分段马斯京根模型计算入流过程（INQi）。

（4） 用入流过程（INQi）减去出流过程（OTQi），得到滞留过程（DQi），保留大于0的DQi连续过程，并与所选的持续上涨水位（Hi）过程比较，若两过程的时间基本一致，则进入步骤（5）;否则，重新调整新安江模型与分段马斯京根模型参数，返回步骤（3）。

（5） 对滞留过程（DQi）逐时计算时段水量（DWi），计算公式为DWi=DQi×DT×3600/1000000。

（6） 求时段水量DWi的累积过程Vi，计算公式为Vi=ij=0DWj，得到样本（HiVi）。

（7） 采用多项式最小二乘法拟合样本（HiVi），得到库容曲线（H～V）。

为了获得准确且可靠的库容曲线，可选择大、中、小不同代表性的典型洪水过程样本，分别拟定库容曲线，再通过坐标平移的方式将这些库容曲线绘在一起，最后综合分析得到一条可以提供给平原区河系实用洪水预报模型使用的库容曲线。

1.4 验证计算指标

为了评判平原区河系实用洪水预报模型计算效果，采用平均绝对误差（MAE）和纳什效率系数（NSE）[14]分别对模拟与实测过程的水位和拟合程度进行控制。MAE越接近于0，表示模拟水位与实际水位相差越小。NSE取值在0～1之间，其值越接近1，表明模拟过程与实测过程拟合程度越优。MAE与NSE计算公式如下：

MAE=1nni=1|Hsim，i-Hobs，i|=1nni=1ei（3）

NSE=1-ni=1（Hobs，i-Hsim，i）2ni=1（Hobs，i-H-obs）2（4）

式中：Hsim，i和Hobs，i分别表示模拟和实测的水位序列，m;ei为绝对误差，ei=Hsim，i-Hobs，i;H-obs为实测水位过程的均值，m。

2 应用实例

2.1 流域概况

本研究选取滁河流域晓桥站为研究对象开展模型的验证。滁河位于江淮之间，系长江下游左岸一级支流，干流全长224 km，流域面积约8 000 km2。流域内水系发达，水流错综复杂，既受上游径流汇入作用又受长江干流下游回水顶托影响。流域内有雨量观测站37个，主要水库站9个，主要水文水位站14个（见图2），除水库站没有长系列资料外，基本都可以提供长序列的雨量或水位观测资料，但流量资料只有少许。其中，晓桥站位于江苏省南京市浦口区永宁镇，该站是滁河水旱灾害防御的关键控制站，为国家重点水文站，本文将以此为对象开展分析。

基于滁河河系主要控制站的空间拓扑关系和水力联系，结合本文提出的实用洪水预报模型，构建滁河河系的洪水预报体系（见图3），其中晓桥站虚拟水库的入库流量主要由上游襄河口来水和区间来水两部分组成。按模型结构需要率定新安江模型、分段马斯京根模型的参数和拟定水库调洪演算模型的泄流曲线与库容曲线，现选取2010～2018年多场次洪水过程开展模型率定，采用2015年6月、2016年7月、2018年8月、2020年7月4场洪水过程进行检验，并采用该模型开展2020年大洪水过程的应用实例分析。

2.2 模型率定及检验

基于2010～2018年实测资料，模型计算步长采用1 h，率定各站虚拟水库的新安江模型、分段马斯京根模型参数和拟定各站虚拟水库的水库调洪演算模型的泄流曲线与库容曲线，以此完成各站预报模型的构建。其中晓桥站的新安江模型与分段马斯京根模型参数见表1，参数取值满足其物理意義，符合该流域实际应用的取值范围，较为合理。晓桥站的泄流曲线和库容曲线如图4所示，可以发现，所拟定的库容曲线与真正意义上的水库库容曲线形状存在较大差异，其主要原因在于：虚拟水库库容曲线主要基于所拟定的泄流曲线，以模型模拟的涨水过程与实测水位过程的吻合程度为主要判别标准，并以水位预测准确为最终目的，通过试错分析得到，实质为理论计算曲线，故可能与实际测量的河道槽蓄曲线在形态上存在较大差异。

对率定期及检验期洪水样本的水位误差进行分析，结果见表2。

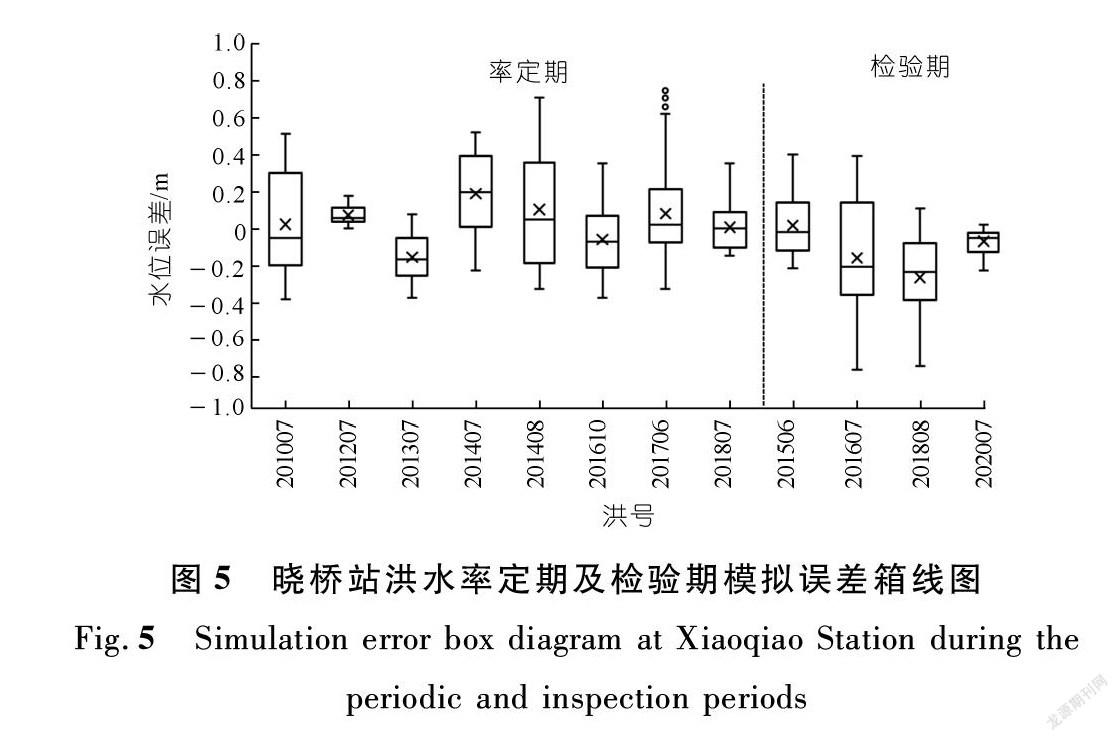
从洪水模拟效果统计表2来看，率定期采用的8个次洪样本的纳什效率系数NSE均值为0.87，绝对误差MAE均值为0.18 m，洪水峰时相对误差为2.6 h;检验期NSE为0.85，MAE为0.20 m，洪水峰时相对误差为1.8 h，模拟效果总体较好。根据上述计算结果，绘制箱线图（见图5）。通过图5可以发现：率定期中值分布范围在[-0.18，0.19]，误差上下限范围[-0.39，0.75];检验期中值分布范围在[-0.25，-0.03]，误差上下限范围[-0.79，0.39]。按率定期、检验期分别统计满足洪峰水位误差在0.2 m以内、峰时绝对值在6 h以内的合格率，并结合纳什效率系数绘制三维雷达图（见图6）。由三维雷达图可以发现，无论从洪峰、峰时还是洪水过程3个维度来看，模拟效果均呈现均衡的状态，因此，可以说明该模型在平原区滁河控制站晓桥站的模拟效果总体较好。

对检验期2015年6月、2016年7月滁河两次明显涨水过程的模拟效果进行分析，如图7～8所示，“201506”洪水峰时误差为16 h，纳什效率系数NSE为0.96，洪峰水位误差为-0.02 m，说明其峰时模拟效果相对滞后，但洪峰水位与洪峰过程总体模拟效果较好;而“201607”洪水峰时误差为-10 h，NSE为0.66，水位误差为-0.09 m，洪水过程与峰现时间的模拟效果一般，但洪峰水位模拟较好。

2.3 应用及探讨

2020年长江发生流域性大洪水，6月下旬至7月下旬，累积面雨量较同期均值偏多1.5倍。受强降雨影响，流域多站发生超历史洪水，晓桥站超警，六合超保证。其中，7月11～19日，滁河连续发生3次移动性的强降雨过程，16～19日为最强过程，在实际运用中基于该模型结合专家经验校正，较为准确地完成了预报。在7月19日08：00制作的预报时，模型输入为19日前实况降雨以及19～21日欧洲中心降雨数值预报，预报分析结果如图9所示。可以看出19日预报结果与实测水位吻合度较高，其纳什系数NSE和平均相对误差MAE分别为0.90和0.08 m，其模拟洪水洪峰水位为11.99 m，峰现时间为20日00：00，实测洪峰水位为12.00 m，峰现时间为20日01：00，模拟峰值较实测仅偏低0.01 m，模拟峰时较实测仅提前1 h，可以看出其洪峰量级和峰现时间预报效果较好。此次洪水期间，晓桥站上游破圩分洪，分别于7月19日02：49、03：26对全椒荒草三圩（在距襄河口闸3.07 km上游左岸干堤处）、荒草二圩（在距襄河口闸4.87 km上游左岸干堤处）实施爆破泄洪[15]，破圩后襄河口虚拟水库的容积被动增大，故在模型实时计算时对库容曲线进行了修正，以期获得襄河口准确的水位及下泄流量预报过程，进而为晓桥站提供可靠的预报入流过程。与此同时，长江干流长时间处于高洪水位，对滁河分流入长江的分洪道（如晓桥水文站上游驷马山引江水道）有明显的顶托作用，分流入江流量较小，故模型实时计算时不考虑分洪道分流入江的影响。在此次预报实践应用中，及时准确的预报成果为成功应对滁河“202007”洪水提供了强有力的防洪决策支持。

在平原区河系实用洪水预报模型的近年实际应用中可发现，通过将平原区河道虚拟为水库模型，同时结合实时校正技术，可显著提升平原区洪水的预报效果，较传统预报方案（仅有洪峰水位相关图方案）略优，不仅可以预报洪峰水位，还可以实现水位过程计算。但同时该模型也具有一定的局限性，即针对虚拟水库所拟定的“泄流曲线”并不能完全反映平原区河系的闸门操控特性，如不同闸门开度可能会导致同水位量级流量不同，进而影响部分场次洪水的模拟效果，因此该模型仍有进一步改进的空间。再者，该模型只针对平原区河系开展了有益尝试，对于其他下垫面条件的河系的适用性还有待进一步探索实践。

3 结 语

本文提出了基于耦合新安江模型、分段马斯京根模型与水库调洪演算模型的平原区河系实用洪水预报模型，该模型一定程度解决了传统水文水力学模型资料要求高、建模复杂、精度不高、过程模拟不全等问题，并在2020年长江流域性大洪水中，在长江下游重要一级支流滁河流域开展了实践应用并取得了较好的预报效果，为滁河流域的洪水调度决策提供了重要依据。由于该模型资料局限性低、建模过程简易、能较好地模拟平原区河系的水位过程，具有较强的推广应用价值，因此对于此类平原区河系水文预报具有较高的参考价值。

参考文献：

[1] 白立影，朱慧娈.平原地区洪水预报问题研究[C]∥第五届中国水论坛论文集，南京，2007.

[2] 芮孝芳，姜广斌，程海云.考虑回水顶托影响的水位预报研究[J].水科学进展，1998，9（2）：124-129.

[3] 何翠敏，刘菊，柏正林.安徽滁河雨洪特性及与长江洪水遭遇组合分析[J].水科学与工程技术，2015（4）：6-9.

[4] 张真奇，夏自强.洪水预报水文水力学模型研究[J].河海大学学报（自然科学版），2002（5）：83-86.

[5] 张端虎.相关图洪水预报方案电算处理方法探讨[J].水利水文自动化，2009（1）：47-50.

[6] 包为民.水文预报[M].4版.北京：水利水电出版社，2011.

[7] 季益柱，龚荣山，焦创，等.基于降雨径流的平原河网水动力模拟[C]∥全国水力学与水利信息学大会.中國水利学会论文集，北京，2013.

[8] 孙映宏，姬战生，王玉明.MIKE11在平原河网地区防洪分析中的应用[J].水利水电科技进展，2008，28（增1）：37-40.

[9] 戴凌全，戴会超，蒋定国，等.基于最小二乘法的河流水位流量关系曲线推算[J].人民黄河，2010，32（9）：37-39.

[10] 刘亚坤.水力学[M].北京：中国水利水电出版社，2008.

[11] 中华人民共和国水利部.水闸设计规范：SL 265-2001[S].北京：中国水利水电出版社，2001.

[12] 张晓波，郑雄伟.平原河网的开敞式水闸过流计算方法[J].中国农村水利水电，2013（9）：104-107.

[13] 宗航，李承军，周建中，等.POA算法在梯级水电站短期优化调度中的应用[J].水电能源科学，2003，21（1）：46-48.

[14] NASH J E，SUTCLIFFE J V.Review flow forecasting through conceptual models part I：a discussion of principles[J].Journal of Hydrology，1970，10（3）：282-290.

[15] 张锦堂，洪建智，朱琼，等.2020年滁河洪水调度实践与分析[J].中国防汛抗旱，2021，31（3）：32-35.

（编辑：谢玲娴）

Discussion on application of flood forecasting model for river system in plain area under complex hydraulic conditions

CHEN Yubin，XIANG Tianyuan

（Hydrology Bureau，Changjiang Water Resources Commission，Wuhan 430010，China）

Abstract：

For flood forecasts in plain river systems under complex hydraulic conditions，traditional hydrological and hydraulic models have problems such as high demand for modeling data，complex processes，and poor simulation results.In this paper，by taking the plain river system as a virtual reservoir model，we proposed a practical flood forecasting model for the river system in the plain area，in which the Xinan River model，the segmented Muskingen model and the reservoir flood regulation model were combined.The Xiaoqiao Station in the Chuhe River Basin was selected as the research object，and the model was calibrated and tested with flood samples from 2010 to 2020，and the flood in 2020 was taken to explore application.The results show that the flood forecasting model has low data limitation and simple modeling process，and can better simulate the water level process of the river system in the plain area，which can provide reference for river hydrological forecasting in plain areas.

Key words：

flood forecasting model;river system in the plain area;Chuhe River Basin;extraordinary flood of Changjiang in 2020