基于健康监测数据的简支梁桥钢筋锈蚀分析

郭 强

（山西交控集团 大同北高速公路管理有限公司，山西 大同 037000）

在桥梁管理系统中，桥梁健康监测作为提供桥梁状况持续信息的手段应用越来越普遍。由于其初始成本较高，与单纯进行传统的检测手段相比，其附加值和长期的显著优势需要得到验证，以便使其成为桥梁管理中常见做法的一部分。然而，目前传感器数据与评估的桥梁安全性或可靠性之间的联系还不强。提高健康监测数据在桥梁管理中的方法之一是将其应用在桥梁风险概率评估模型中，这样就有可能利用这些数据来提高对桥梁安全性的评估[1-2]。近几十年来，桥梁风险概率评估一直是各种研究的热点。人们普遍认为，根据新结构的设计标准对现有桥梁进行加固是保守的，可能导致不必要的更换或修复。使用风险概率评估并量化适合桥梁状态的实际风险有助于避免不必要的成本和资源消耗。显然，准确量化和限制概率模型中涉及的不确定性是很重要的。限制不确定性或改进此类模型的一种方法是在桥梁使用寿命期间收集有关桥梁的新信息，例如，在检查期间收集损伤指标数据，并通过前后分析更新概率模型。

不同的监测技术和周期性数据采集在结构安全评估领域有不同的用途。利用桥梁能够服役到现在或在验证荷载作用下运营状况的事实，可以修正结构承载力的估算结果。桥梁健康监测系统可以通过分析已经经历过的实际荷载，并修正评估模型，来提高桥梁安全性的评估准确度[3-4]。本文利用基于健康监测数据的损伤指标，对锈蚀引起的钢筋损失进行了过程更新。本文的目的是评估损伤指标，并比较它们在桥梁锈蚀损伤状态信息质量方面的有效性。这是通过贝叶斯更新将它们合并到概率锈蚀模型中来实现的。

1 基于桥梁SHM系统的损伤评估指标

本文讨论了基于不同SHM系统的损伤评估指标。损伤指标是在概率背景下建立的，即监测期间的随机环境交通条件，因此假设监测期间没有交通限制。所有损伤评估的目标是提供修正桥梁安全评估结果的方法。

1.1 基于应变的损伤指标

应变监测成本低，可以准确测量桥梁的局部应变响应。近年来，基于光纤的应变监测方法发展迅速，被认为是最有前途的长期应变监测工具。它们的主要优点是耐锈蚀性、对电磁干扰不敏感。在本研究中采用光纤应变计，应变在主梁底面跨中布置。

1.2 基于挠度的损伤指标

与应变不同，某一点的挠度不仅受该点的位移影响，还受整个结构的抗弯刚度分布的影响。目前各方面性能和精度都较为可观的方法是使用摄像机和图像处理技术来监测挠度。这种方法成本低廉，是一种快速发展的新技术。这种方法是使用一个摄像机跟踪桥上一个点的历史位移，在短跨径简支桥梁的实际应用情况下，可以安装摄像机，对准聚焦在通常出现最大挠度的跨中位置附近的点。在一定交通条件下可以准确快速地获得跨中挠度数据的时间历程。

1.3 基于转角的损伤指标

测斜仪用于测量转角的变化角度，包括桥梁的转动变形。基于加速度测量的特殊测斜仪目前已经存在，并且精度较高。与挠度或应变相比，倾角监测的一个显著优点是，即使传感器被放置在桥梁的支点上，也可以从信号中提取有用的信息，安装位置通常比其他区域（如中跨）更容易接近。

2 退化钢筋混凝土结构的随机建模

2.1 钢筋混凝土桥梁的刚度

钢筋混凝土桥梁的刚度可以用其几何参数和材料参数来计算，这些参数通常是随机的。在设计新桥时，可根据设计规范定义的这些参数计算保守的非理想值。通过这种方法，概率问题被转化为一个非单调问题，在设计阶段使用起来简单得多，只会产生最小的额外成本。然而，对于现有的桥梁，更精确的概率方法通常是保守的、高成本的。同时，本研究仅考虑抗弯刚度的时间变化是通过退化过程即钢筋锈蚀来解释的。

2.2 锈蚀模型

锈蚀是钢筋混凝土结构寿命中最重要的劣化过程。由于钢筋面积的损失，它会导致横截面的弯矩承载力迅速损失。在本研究中，仅考虑均匀锈蚀，对于锈蚀模型，其他参数也可以视为空间变化，例如梁的几何特性、表面氯化物含量或混凝土保护层厚度，但为了简单起见，并且由于预计它不会对损伤指标的比较产生重大影响，因此本文不考虑这一点，用钢筋锈蚀面积的随机变化过程表示锈蚀模型。

3 贝叶斯更新

3.1 基本假定

如前所述，锈蚀是钢筋混凝土结构的主要劣化过程。锈蚀的影响可分为：钢筋区域的收缩、钢筋和混凝土之间黏结强度的降低以及钢材极限强度的降低。钢筋锈蚀也可能导致混凝土开裂和剥落，从而导致非线性劣化率[5]。然而，为了确定安全性和监测数据之间的基本关系，锈蚀模型尽可能简单。因此，为了模拟，本文只考虑了锈蚀的面积损失效应。

锈蚀模型涉及大量的不确定性和对不同变量的依赖性，这些不确定性和依赖性在高置信度下难以获得，并且随时间而变化。当在同一结构上的不同时刻进行监测时，有可能获得有关锈蚀演变发展的一些信息。本文利用损伤指标来获取桥梁抗弯刚度变化的信息，从而间接反映钢筋锈蚀引起的面积损失。

3.2 分布函数

在此基础上，可得到锈蚀模型的先验分布。在检查时，假设桥梁的年龄和环境的侵蚀性是已知的，因此通过随机锈蚀模型，可以获得实际钢筋面积损失的一些估计值。本文采用蒙特卡罗模拟方法，得到了给定时刻剩余钢筋面积的经验分布。然后，利用建立良好的分布拟合技术可以找到在某一时刻最适合模拟数据的分布和参数。此拟合分布可用作模型修正过程的先前分布。

3.3 贝叶斯定理

应用Bayes定理，结合新获得的健康监测数据，改进先验模型是可能的。这种情况下的先验分布是钢筋锈蚀面积损失的概率密度函数，新数据来自损伤指标。根据贝叶斯定理，改进的概率密度函数可以写成：

式中：π(θ)是参数向量为θ的先验分布；x是新观测的向量；p(x/θ)是给定θ的x的条件概率密度函数。后者也被称为似然函数。等式的分母是一个标准化常数，因此后验概率密度函数与似然函数和前验概率密度函数的乘积成正比。

3.4 马尔可夫链蒙特卡罗方法

后验分布的解析解只存在于特定情况下，即先验分布和似然分布是共轭的。本文利用Metropolis-Hastings算法应用马尔可夫链蒙特卡罗（MCMC）方法。原则上，它使用马尔可夫链随机游走直接从后验分布中采样[6]。该算法在马尔可夫链随机游动的每一步随机选择6个值，以预先定义的超优先级为条件，并根据接受规则接受或拒绝。

4 实例分析

4.1 分析步骤

总体分析步骤可按图1所示进行。

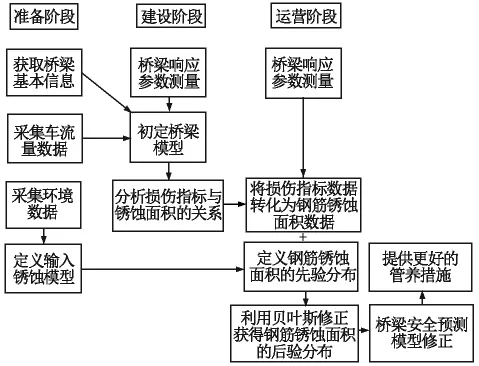
图1 总体分析步骤

4.2 工程概况

本文考察的桥梁为一座20 m跨径的钢筋混凝土空心板简支梁桥，桥型简单且不影响本研究的重点方法。初始状态健康桥梁（t=0）的随机变量见表1。运营期间（t=x）可使用从锈蚀模型中获得的一定程度的钢筋损耗。假设桥梁的年龄和环境的侵蚀性是已知的。因此，可以在概率和时间相关的情况下计算桥梁的锈蚀损伤程度。

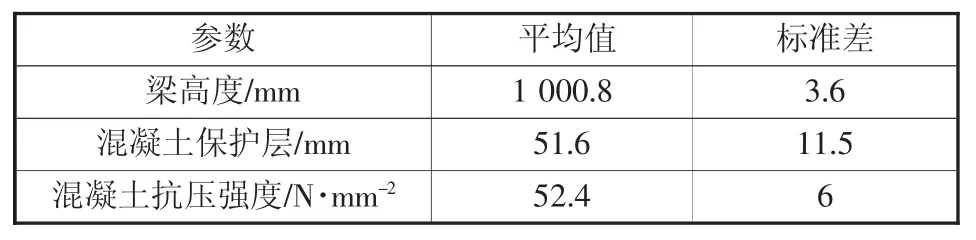
表1 用于初始状态建模抗弯刚度的随机参数

4.3 监测程序和损伤指标

该桥监测了应变、挠度和倾角参数，在相同的交通条件下，忽略桥梁几何结构、材料特性等相关变量的不确定性，各个监测参量考虑一个测点。因为是简支梁的缘故，本研究忽略温度对传感器精度和桥梁荷载响应的影响。因此，结果的变化仅由环境车流量的变化和假设的传感器分辨率引起。比较不同的损伤指标，可以了解它们对损伤的敏感性以及不同交通条件的影响。考虑15%～30%的钢筋面积损失和20～50组数据采集（每次重复两个小时的数据收集）。这意味着结构中的锈蚀程度相当于钢筋面积损失的15%～30%，收集相当于40～100 h的数据。

利用3年的动态称重（WIM）数据和荷载响应数据，建立了基于不同监测值的损伤指标模型，模拟实桥交通。该WIM数据来自2016年至2019年间。这些数据包含有关车轴数量、车轴间距、车轴重量和车速等信息。分别为每辆汽车提取响应信息，在获得不同车辆的单独响应后，将损伤指标计算为数据区间的平均值或两小时内单个信号峰值的平均值，如表2所示。

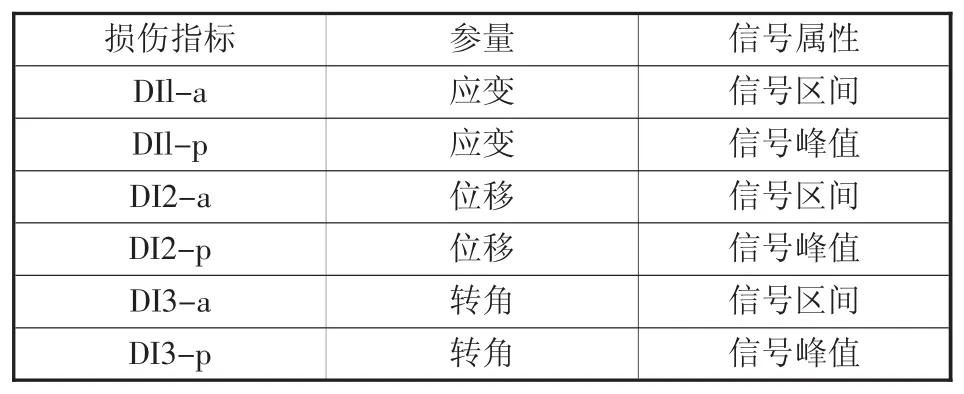
表2 损伤指标

将数据库划分为11个子集，对应11个不同的锈蚀等级，即0、5%、10%、…、50%。50%的锈蚀度是非常高的，线性弹性行为的假设在这一点上可能不再适用，但它被包括在内，以便可以看到损伤增加的趋势。将数据库划分为子集可确保与每个锈蚀等级对应的数据是独立的。由于原始数据库由3年的数据组成，每个子集对应3/11年的数据（大约450个2 h的工作时间流量块）。

图2展示出了3种不同损伤水平的DI3-a（转角）值的分布直方图。相对于健康桥梁（As=0%），可以看出，在环境噪声和交通荷载随机的前提下，DI3-a也有相当大的变化。随着损伤的增加，该图向右移动，反映了由于刚度降低而导致的转角增加，说明损伤指标确实能够反映钢筋锈蚀的变化情况。

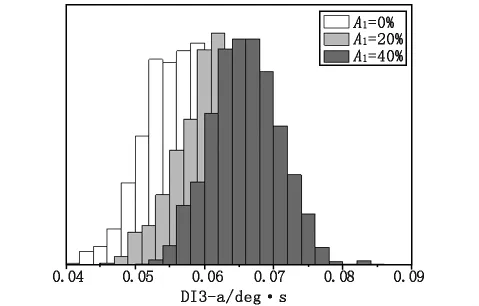
图2 不同锈蚀度下转角分布直方图

Al=0%、Al=20%和Al=40%的直方图分布具有明显差异。在图3中绘制出经过数据标准化处理后，所有6组数据的平均值、平均值±1个标准差（SD）的损伤指标。对于所有6种损伤指标，趋势是单调的，平均值在50%损伤水平下增加或减少一倍。

通过图3可知，所有6种损伤变化的趋势是单调递增的，在50%锈蚀水平下，平均值增加约一倍；然而在大多数情况下，损伤指标的可变度是非常高的，其中DI1-a具有最高的可变性。监测指标显示出的变化幅度很大程度上是由监测中的环境噪声水平驱动的。这些监测指标可直接用于触发任何检查或维护操作。例如，触发警报的阈值情况可能是一个标准差数值大小的概率钢筋锈蚀面积达到20%。

4.4 贝叶斯更新

可以使用图3的平均值曲线计算损伤指标并将其转换为锈蚀面积数据。然后，利用给定年份对应的锈蚀面积分布和选择的锈蚀模型作为先验分布，并将实时测量得到的锈蚀面积数据转换成MCMC。用这种方法可以得到每个测量集合的锈蚀面积的后验分布。然而为了在本研究中进行测试，还按照以下步骤分析监测数据：

a）定义案例分析中的“实际”锈蚀面积。

b）提取6个损伤指标的直方图如图2所示，对应实际锈蚀面积。

c）利用核密度估计来更好地表示所有可能的监测数据。

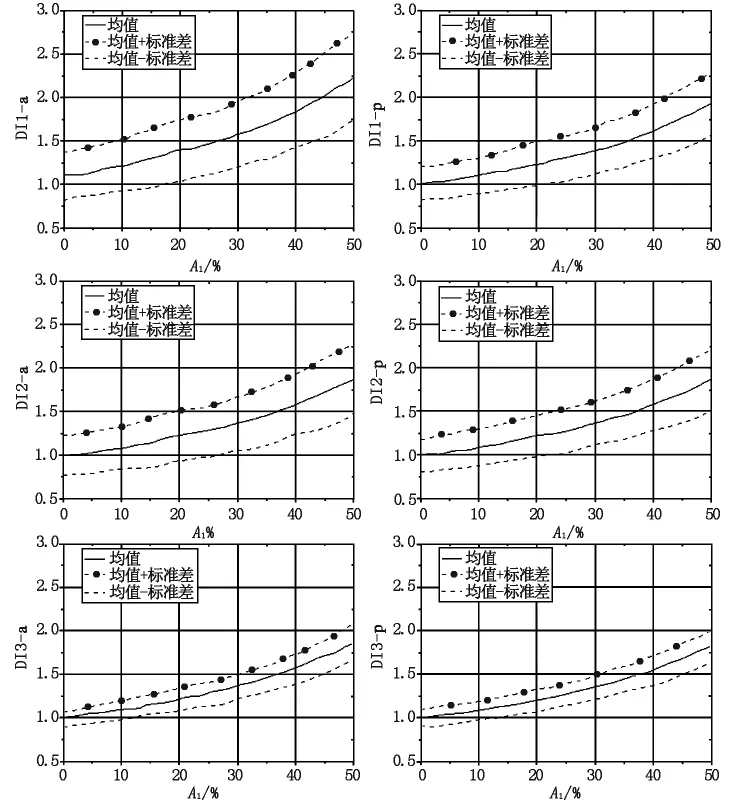
图3 钢筋面积损失在0%到50%之间的6种损伤指标标准化后的变化趋势

d）从每个监测数据样本的监测指标密度分布中随机抽样。

假设MCMC退化时间设置为100年，单位坐标设置为20，每次更新考虑步骤的1 500个净数据量的Markov链随机游动。合格率随模拟而变化，但保持在0.15到0.35之间。后验参数取1 500个链点随机游走样本的平均值，从而得到伽马分布的k和λ参数。使用20和50组监测数据，在两个获得的后验密度分布示例基础上直接建立后验伽马分布，如图4所示。

图4 锈蚀面积的先验分布和更新后的两个后验分布示例

4.5 结果

对于本案例研究（图4），使用先前分布的期望值约为35%。当先验的期望值与实际值相距较远时，更新后的估计值明显偏高。然而，当期望先验值已经很好时，更新可以降低估计值。分析结果见表3。

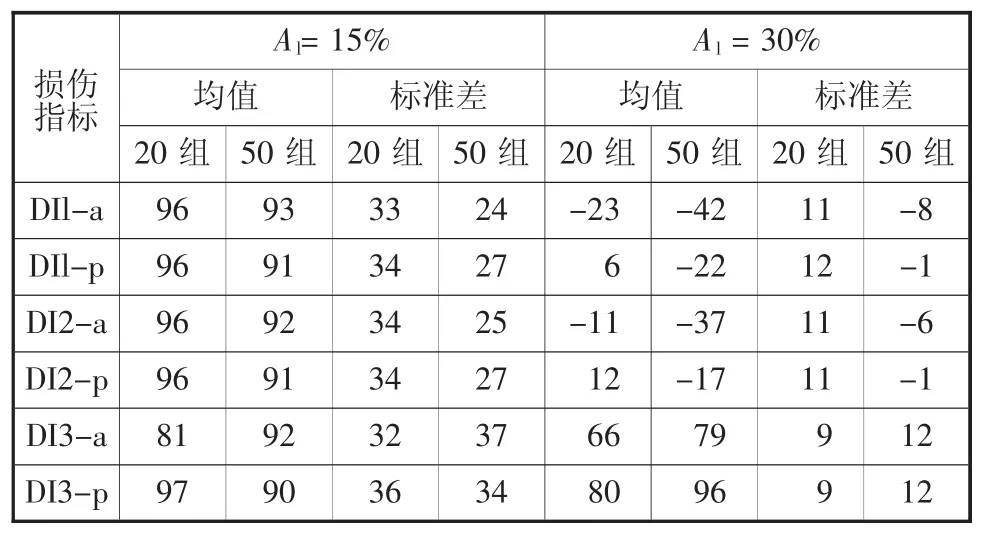
表3 改进了平均值和标准差的先验估计

可以看出，当实际Al=15%时，在所有情况下，更新显示出与先前估计相比的改进，并且在许多情况下，实际值在预期值的一个标准偏差内。对于Al=30%的情况，DI3-a和DI3-p的表现优于其他指标。比较20次和50次监测的结果，可以看出，随着数据量的增多标准差会降低，因为采集次数越多，数据的分布范围就越广。监测数据越多，结果就越稳定，平均值和标准差的变化越小。

观察关于Al分布的标准差可以看出，当锈蚀面积实际值等于15%时，所有损伤指标的质量（表中的正值）都比先前的估计值有所改善，而当实际值=30%时，它们在所有情况下都不能发生改善（表中的负值）。特别是对于DI1和DI2，当使用20组监测数据而不是使用50组监测数据时可以获得改善。对于DI1和DI2的20组监测数据，标准差结果更好，因为进行的测量越多，测量数据的传播范围就越广。然而，对于DI3，当测量数据的分布较小时，可以通过更多的监测数据获得更好的结果。可以看出，当有50组监测数据时，不同的损伤指标之间有很大的差异。另一方面，当只有20组监测数据时，损伤指标的表现彼此类似。

可以看出，监测数据越多，结果就越稳定，平均值和标准差的变化越小；然而，这并不一定会带来更好的结果。增加监测数据量分析时，只有当监测数据本身是完美的，才能获得几乎完美的模型。由于模型所涉及的不确定性和随机性，每个损伤模型在性能方面都有一个限制，超过这个限制，增加监测数据量本身并不能改善甚至可能恶化更新的总体质量。

5 结语

本文提出了一个利用不同健康监测数据更新桥梁安全评估的框架。对一座钢筋混凝土空心板梁桥进行了概率建模。基于锈蚀模型，模拟结构随时间变化的特征。基于应变、挠度和转角监测的各种损伤指标，在随机动态交通条件下进行分析，并用于更新锈蚀钢筋面积损失的概率分布。比较了不同损伤指标的后验分布。利用所提出的框架，可以评估和比较来自不同监测指标的数据。比较的关键是损伤指标对损伤的敏感性和结果的可变性。这可以是建立桥梁健康评估系统的第一步，最终结果也有利于更优化的健康监测系统设计。