基于MPL神经网络的地震作用下砂土液化评估及预测*

杜 星 孙永福③ 宋玉鹏 宋丙辉 赵晓龙 宋莎莎④ 王 越

(①自然资源部，第一海洋研究所，青岛 266061，中国)(②青岛海洋科学与技术国家实验室，海洋地质过程与环境功能实验室，青岛 266235，中国)(③国家深海基地管理中心，青岛 266237，中国)(④南京大学，地理与海洋科学学院，南京 210023，中国)

0 引 言

地震引发的砂土液化是一种极具破坏性的地质灾害现象，液化发生后会破坏农田、道路、桥梁以及各种民用建筑、水利设施，给社会经济和人类生命安全都造成巨大的危害。因此，地震作用下的砂土液化一直是岩土工程领域和灾害地质领域研究的热点问题之一。由于地震的发生是不可避免的，因此对场地进行地震液化的可能性评估和预测是该问题研究的重点方向。

当前进行地震液化的判别方法主要分为两大类：一是以地震现场砂土液化灾害调查资料为基础建立的经验分析法，二是基于现场或室内试验建立的试验分析方法(张源等， 2019)。其中经验分析法主要包括常用于规范的标准贯入法、临界孔隙比和能量判别法(Ishac et al.， 2010)等； 试验法主要包括Seed-Idriss简化法(Seed et al.， 1971)、剪切波速法(Dobry et al.，1982)、静力触探法(Robertson et al.， 1988， 蔡国军等， 2008， 李兆焱等， 2010， Robertson， 2015)、动单剪试验、振动台试验(Ling et al.，2003， Ha et al.，2011， Varghese et al.， 2014)以及动三轴试验(周键等，2011， Yu et al.，2012， Qing et al.，2017)等。近年来，基于机器学习的研究方法在地球科学领域的应用逐渐兴起，传统的地质研究正逐渐向数据深度挖掘、大数据和人工智能领域靠拢，例如在地层序列(周翠英等， 2019)、滑坡(汪发武， 2019， 杨帆等， 2019)等方面的研究。在地震液化的研究中，蔡煜东等(1993)较早地应用BP神经网络进行了砂土液化预测。 Xenaki et al.(2003)、 刘红军等(2004)、 Hanna et al.(2007)、 李标等(2008)、 Ramakrishnan et al.(2008)、 Juang et al.(2010)、 Xue et al.(2017)分别基于神经网络理论进行了扩展研究，通过对现有液化数据和资料进行学习和训练，建立沉积物参数、地震参数与液化情况的非线性耦合关系，并尝试将神经网络与遗传算法(Xue et al.， 2017)、傅里叶变换(Bi et al.，2018)等算法相结合。

目前已提出的用于解决地震液化问题的神经网络大部分是朝着模型设置复杂化的方向发展，尽管模型种类丰富但受数据量的影响精度提升有限。为了在简化模型构建的同时满足地震液化预测的精度，本文在当前地震液化和人工神经网络研究的基础上，通过对神经网络参数和内置传递函数进行详细试验和判别，建立基于MPL神经网络的地震作用下砂土液化判别模型，并详细讨论每个输入参数对液化结果预测的影响程度以探究是否可以对模型进行简化。

1 神经网络算法

人工神经网络(Artificial Neural Networks， ANN)是一种典型的有监督机器学习算法，通过模仿自然界生物神经元之间电信号的传递并由大量节点之间相互连接组成。其中，多层感知器网络(Multilayer Perceptron， MLP)是当前最流行的前馈人工神经网络之一。典型的MLP神经网络通常包含输入层、隐藏层(一层或多层)以及输出层(图1)。输入层与输入变量有相同数量的节点数； 隐藏层包含了神经元之间连接的权重值以及相应的阈值函数，用来传递和处理信号； 输出值即为最终要得到的数据。

图1 前馈神经网络示意Fig.1 Illustration of feedforward neural network

前馈神经网络在数学上的表示为：

(1)

(2)

式中：x为输入参数；ωih和ωho分别为输入层-隐藏层权重、隐藏层-输出层权重；bih和bho为偏差参数；M为隐藏层的节点数；d为输入层的节点数；Tr(z)为传递函数，该传递函数对求和输入进行非线性转换。

算法的目标为通过一系列的训练，减小计算值与真实值之间的误差，误差E可定义为：

(3)

式中：p为训练模式总数；Ep为第p次训练模式的误差。由下式得到：

(4)

式中：N为输出节点总数；k为第k次输出节点的输出；tk是第k次输出节点的目标输出。

每计算出一次误差后，将向前进行反馈并更新权重值，使网络更能接近实际的表达值，直至所有训练数据训练完毕。对于一组训练数据通常会进行多次训练，每训练一次称为一个世代(Epoch)，一般训练达到设定的参数条件后停止。

2 砂土液化预测网络建立

2.1 研究数据

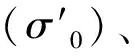
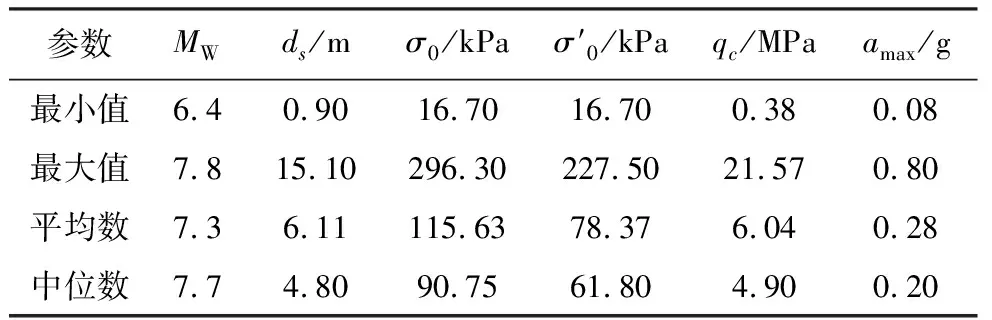
表1 地震作用下砂土液化参数统计Table1 Parameter statics of earthquake-induced sand liquefaction

2.2 神经网络构建

在神经网络构建时隐藏层的层数和节点数非常重要，目前为止还没有研究能够明确地得出一个研究问题中最佳的隐藏层数和节点数。因此在进行具体问题的神经网络构建时，需要根据实际数据的参数进行合理的尝试并得到较为优化的网络。由于输入参数为6个，因此本文中的砂土液化预测网络输入节点数目为6(图2)。另外，因为砂土液化网络得到的结果为液化(1)或不液化(0)两种结果，所以输出节点数目为1。

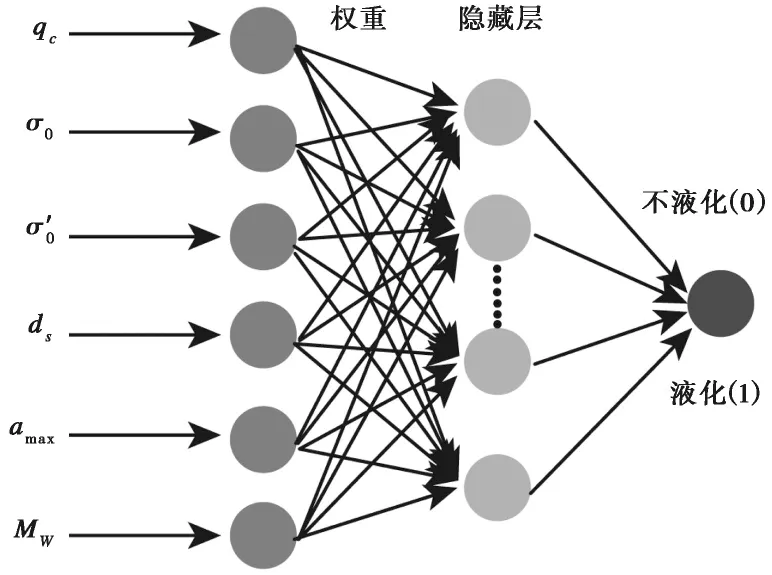
图2 砂土液化判别神经网络结构Fig.2 Structure of sand liquefaction assessment neural network

隐藏层节点数经验判别公式为：

(5)

式中：m为隐藏层节点数目；n为输入层节点数目； l为输出层节点数目；a为1～10间的常数。

根据上式得出最佳隐藏层节点数应在4～14个之间，为增加准确率本文将扩大试验范围，对4～18个隐藏层节点数均进行试验。首先定为一层，节点数将会进行不同参数的试探，当一层隐藏层计算结果误差较大时将增加隐藏层数量，直至得出满足问题精度需要的结果。

网络输入参数为基于CPT测试获得的6组相关参数； 数据分割即为将所有数据分割成训练数据、验证数据(用以优化网络参数)、以及完全独立的检验数据，本文采用了最常用的70%-15%-15%分割方法，即使用70%的数据训练网络， 15%的数据优化网络参数， 15%的数据用于检验网络的准确性； 网络结构为6-x-1类型； 常用训练函数类型主要有Levenberg-Marquardt、Bayesianregularization、Scaledconjugategradient3种。目前的理论仍无法直接确定不同问题的最优参数设置，只能根据具体情况进行试探。详细网络模型参数设置见表2，第1组试验用来确定最优的网络隐藏层节点数目，训练函数采用了最常用的Scaledconjugategradient； 第2～4组试验暂定网络结构为6-11-1，分别使用不同的训练函数组成了3个不同的网络用来确定最优的传递函数。通过对不同试验组进行多次试验，分析统计准确率后可以得到满足地震作用下砂土液化判别的最佳网络。使用确定的最佳结构和训练函数的网格对研究数据进行训练并验证其准确率。

表2 神经网络试验参数设置Table2 Parameter settings of neural network experiments

3 结 果

通过对不同隐藏层节点数的15个网络结构分别进行20次训练后，去掉最大值和最小值获得的准确率统计结果见图3。其中，各节点最大准确率均达到100%，表明网络进行了多次运算后有一定几率对训练数据的预测很准确； 网络检验结果最低准确率中最大为82.35%，隐藏层节点数为5、15、16、17和18； 平均准确率中最高为91.5%，网络节点数为8和15； 中位准确率最高为94.12%，网络节点数为8、11、12、14、15和17。综上所述，适用于本研究中地震作用下砂土液化预测的最佳隐藏层节点数应为15。

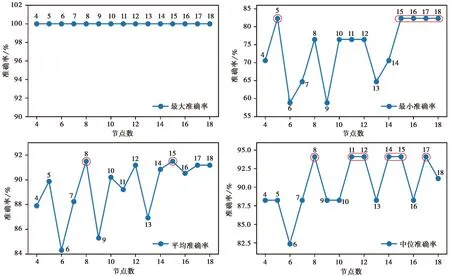
图3 不同隐藏层节点网络准确率统计Fig.3 Accuracy statistics of neural networks with different hidden layer nodes图中，红圈表示该条件下准确率最高的节点数对应数值

当隐藏层节点数相同时，分别对3个网络使用不同训练函数的网络进行了20次训练并进行了验证，准确率统计结果见表3。当使用Levenberg-Marquardt与Scaledconjugategradient函数时，网络训练速度较快； 使用Bayesianregularization函数时，网络训练速度较慢，时间通常为另两种函数的数十倍。同时，无论是最高准确率、最低准确率、平均和中位准确率，Levenberg-Marquardt函数得到的都是最大值。因此，选定Levenberg-Marquardt函数作为本研究中神经网络的训练函数。综上所述，试验结果表明当隐藏层节点数为15、训练函数为Levenberg-Marquardt时，构建的地震作用下砂土液化神经网络模型准确率最高。

表3 不同训练函数准确率统计Table3 Accuracy statistics of different training functions

在使用研究得到的最佳网络进行训练和验证后，得到结果如图4所示。当训练达到第6世代时，验证集存在最小均方误差，因而此时不同网格层之间的权重为最佳结果。使用最终获得的网络对25个检验数据预测并与实际结果进行比对，准确率结果见图5和表4。网络对于12个未液化的案例预测结果显示11个未液化、1个液化，准确率为91.7%，对13个发生液化的案例预测准确率为100%，总体25个案例预测准确率为96%。

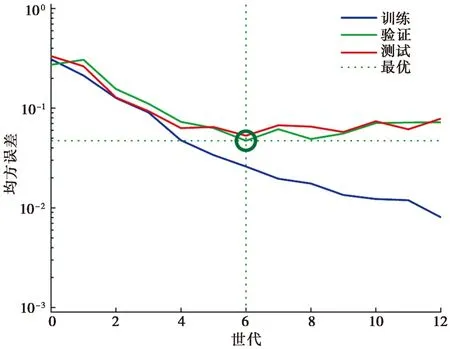
图4 训练过程Fig.4 Training process其中，蓝、绿、红线分别代表了不同世代的训练集、验证集、测试集均方误差，虚线表示验证集最优位置。神经网络精度随着世代增加通常表现为先提高后降低的趋势，存在中间位置的最优世代

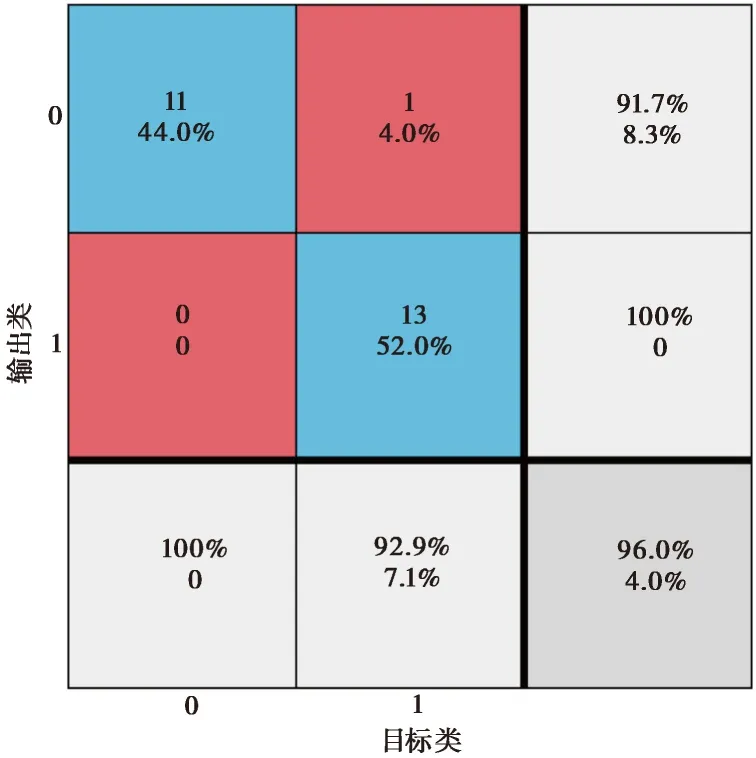
图5 液化结果预测Fig.5 Prediction of liquefaction results其中， 0表示未液化， 1表示液化，同一行或列中蓝色代表预测准确的数目及准确率，红色代表预测错误的数目及错误率，浅灰色代表某一类的准确率，深灰色代表所有样本的准确率

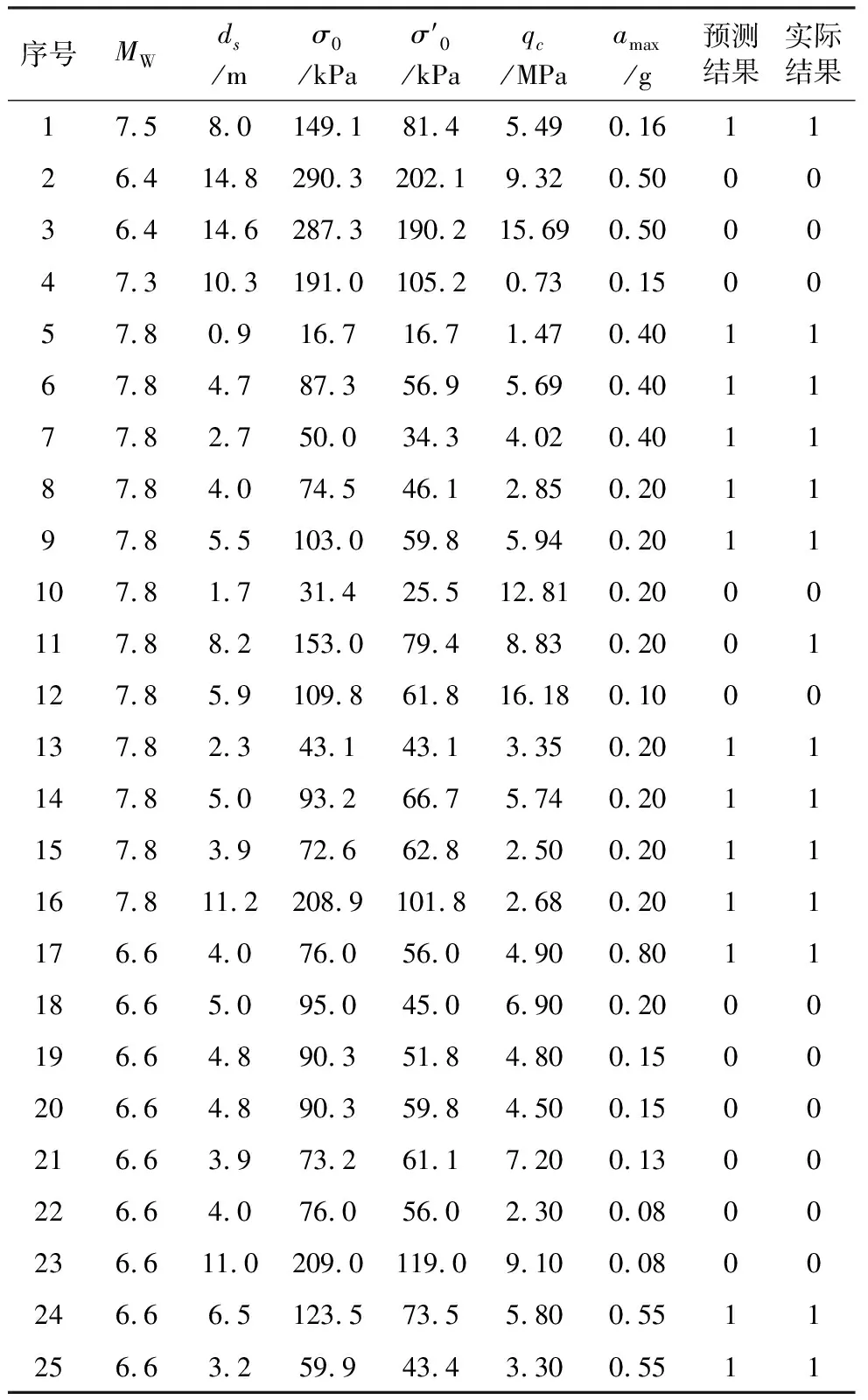
表4 预测结果与实际结果比较Table4 Comparison between prediction results and actual results

4 讨 论

4.1 网络准确性

由于神经网络训练特点为在训练过程中不断通过每一组数据来调整节点间的权重，使得即使相同的数据、算法和参数每次训练得到的网络都略有不同，因此并不存在对于一个问题的最好网络算法，只有相对满足需求和精确度的网络算法。本文针对研究问题特点，选定了隐藏层节点数目、训练函数2个参数来确定最终的网络结构。其中隐藏层节点数目设置为4～23个，在其他参数不变的情况下分别对20个不同结构的网络训练20次，为减小个别极端情况造成的误差，统计时分别去掉了一个最大值和一个最小值。虽然每次训练所得网络测试的准确率都不相同，但是在多次测试结果的统计下仍然能够判断出最适合本研究的隐藏层节点数目。当网络其他参数保持一致，训练函数不同时可构成3个不同网络。使用研究数据分别对3个网络进行20次训练后，可以明显地观察到Levenberg-Marquardt函数无论是在准确率还是训练时间上都占有明显的优势。

使用隐藏层节点数为15、训练函数为Levenberg-Marquardt时的网络对研究数据训练后验证正确率显示为96%，只有1组数据预测错误，这表明训练后的网络能够较好地对基于CPT数据的地震作用砂土液化问题进行学习和预测。准确率为96%并不表示网络无法达到更高的准确率，而是因为验证数据有限，每预测错一个结果正确率就下降4%。由于地质灾害的发生难以确定，能够准确监测并获得有效数据的更少，因而用于神经网络研究的数据量相对较少。尽管当前众多学者均尝试使用各类改进的神经网络模型对地质灾害问题进行预测，并得到了相对较高的准确率(Zhu et al.，2017; Bi et al.， 2018; Hulbert et al.，2019)，但是模型的适用性仍然受到地质灾害数据量过小的影响，这也是当前无法解决的问题之一。另外，由于本文网络使用了基于CPT测得的6个参数进行预测，今后想要使用该网络预测其他区域的液化情况也需要使用上述6个参数，这对于无法提供如此多的参数的地区并不适用。如何解决部分参数缺失条件下的网络预测是今后必要的研究方向。

4.2 输入参数影响程度研究

为研究基于CPT获得的6个参数对于神经网络的准确率影响程度，并探究是否可以在不影响准确率的情况下通过减少输入参数的数目来简化神经网络，开展了以下试验。如表5所示，每组分别去掉了一个参数用以检验缺失该参数情况下的网络准确率，如果去掉某参数后预测准确率下降越大则说明该参数越重要，反之则说明不重要，可考虑简化网络结构。

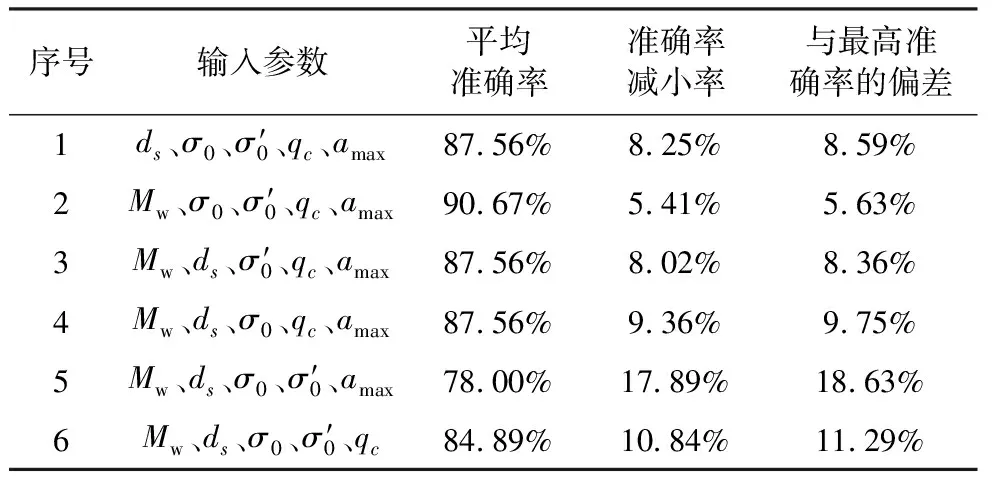
表5 输入参数研究Table5 Study of input parameters

地震震级(Mw)和地表归一化峰值水平加速度(amax)均表示了地震的作用强度，是地震液化问题必不可少的参数。其中，地震震级表示了地震整体烈度，若震源较深或者研究区距离震中很远则无法明确地对表征地震。而地表归一化峰值水平加速度表示了研究区地表受地震影响的程度，相对震级来说更加能够表征地震作用强度，因此缺失了地表归一化峰值水平加速度后准确率下降程度高于缺失地震震级。其余几个参数均表示了研究区沉积物物理力学性质，贯入深度、总垂向应力、有效垂向应力、锥端阻力对准确率的影响程度依次增高表明了从中可获得的沉积物物理力学性质的表征程度依次增高。

5 结 论

本文以神经网络方法为技术手段，对1964～1984年在世界各地发生的166组地震引发的液化数据进行了训练和学习，建立了锥端阻力、总垂向应力、有效垂向应力、贯入深度、地表归一化峰值水平加速度、地震震级与是否发生液化之间的非线性耦合关系。研究表明，使用神经网络方法能够对地震作用下的砂土液化问题进行准确的预测评价，当网络中含有6个输入层节点、15个隐藏层节点、1个输出层节点、训练函数为Levenberg-Marquardt时预测效果较好，对检验数据预测的准确率可高达96%。不同地质参数对神经网络预测结果准确率的影响程度不同：锥端阻力、地表归一化峰值水平加速度对网络预测结果影响较其他参数最为显著，在地震液化问题中起着重要的作用； 地震震级、总垂向应力、有效垂向应力对于网络预测准确率影响处于中等位置； 贯入深度对结果精度影响最小。