基于EPS板减载的不同矢跨比高填黄土明洞土压力及影响因素离散元分析*

赵亮亮 宁贵霞 李 盛 姚玉相 马 莉 韩国强

(①兰州交通大学土木工程学院， 兰州 730070， 中国)(②兰州工业学院土木工程学院， 兰州 730050， 中国)

0 引 言

在西部铁路建设中，为缓解城市用地紧张，高填明洞的应用日益普遍。在实际工程中常常出现因明洞结构型式受力不合理而导致洞顶纵向开裂等问题。为保证明洞结构安全，合理的减载措施必不可少。但当填土高度过大时，仅仅通过减载方式不能完全达到工程的要求，所以有必要通过结构型式优化的方式来进一步增加填土高度，改善结构受力。因此，对不同矢跨比下高填黄土减载明洞土压力的研究具有重要意义。

国内外学者对高填方明洞减载进行了研究，并取得了一定的成果。美国衣阿华州立大学的Marston(1930)最早提出并验证了高填方涵洞(管)结构的ITI卸载法，即在其顶部铺设可压缩柔性材料进行土压力减载； 随后，Larsen et al.(1962)、顾安全(1981)、Valestad et al.(1993)、Okabayashi et al.(1994)、Dancygier et al.(1996)和白冰(1997)通过在结构物顶部铺设柔性材料，研究了结构-土相互作用的影响，进一步得出在结构物顶部铺设柔性材料可以起到很好的减载效果； Lee et al.(2007)采取室内试验和有限元模拟了不同减载措施的减载效果； 姚玉相(2019a)等使用离散元软件，研究了不同减载措施对土拱效应的影响； 李盛等(2014a， 2014b， 2016a， 2016b， 2016c， 2018a)， Li et al.(2019)通过模型试验和有限元软件数值模拟，对高填黄土减载明洞进行了一系列研究，提出了很多有效的减载措施，分析了影响高填黄土明洞土拱效应的各种因素。

有关明洞截面型式的研究，王焕等(2018)通过数值模拟和室内试验的方法，研究了矩形和拱形两种明洞截面型式土压力及土体位移差异性规律，为沟谷地区高填黄土明洞结构截面设计提供了参考； 徐湉源等(2017)和王明年等(2017)分别采用现场测试和数值分析方法对高填方双层衬砌明洞的土压力和结构内力进行研究，得到明洞上方和两侧土体的沉降差分布规律； 高振(2014)使用ANSYS软件研究边坡坡度、沟底与结构的宽度比、结构处于沟底的位置及回填土容重对高回填明洞土压力的影响，拟合出以容重和回填土高度为基本参数的高回填明洞的非线性土压力计算公式； 匡亮等(2013)、杨雄等(2013)和谭永杰等(2017)通过数值计算研究了沟谷山区大跨度高回填明洞衬砌结构受力特性、结构变形及结构选型。

上述研究现状表明，前人已对明洞减载和选型进行了大量研究。但是，对于不同矢跨比下高填黄土减载明洞土压力的变化规律鲜有报道。故本文利用离散元软件PFC2D，分析了EPS板减载下，不同矢跨比明洞顶垂直土压力、竖向位移、明洞侧面水平土压力及颗粒间接触的变化规律，并得到土压力最小时减载明洞的最佳矢跨比。在此基础上，研究了槽宽比和边坡坡角对土压力的影响规律，以期为减载明洞结构选型提供参考。

1 模型建立与细观参数选取

1.1 模型建立

利用PFC2D(颗粒流)程序建立数值模型的过程中，为获得更高精度的初始应力状态模型，减小生成初始模型时的水平土压力，本文采用改进的多层压实法(IMCM)生成初始模型。整个模型中，模型箱总高H=1.3m，明洞宽D=0.2m，沟槽底部宽度B=0.6m，边坡坡角β=70°，明洞高度随着矢跨比的增大而增大，当矢跨比(S/D)为0.4时，明洞高度h=0.18m，以此类推，当矢跨比为0.5、0.6、0.7、0.8、0.9时，明洞高度分别是0.20m、0.22m、0.24m、0.26m、0.28m，其结构示意图如图1。

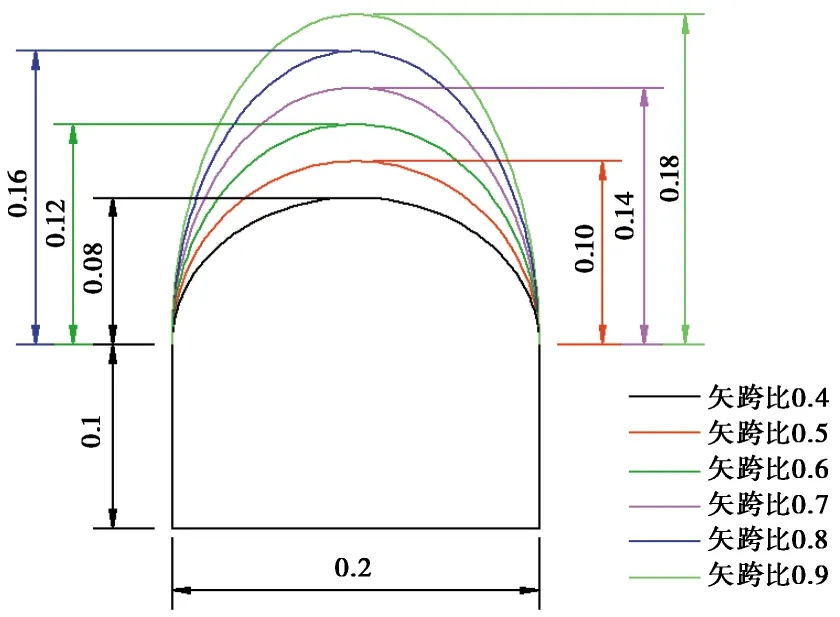
图1 矢跨比变化(单位：m)Fig.1 Variation of height-span ratios(unit：m)

数值模型图如图2所示。在图2中用墙单元(wall)来模拟地基、明洞和沟槽壁。此外，为测量模拟压实过程中各个位置的垂直土压力、水平土压力及颗粒竖向位移的变化，在模型中设置了一定数量的测量圆，其半径为3cm，位置如图2所示。其中，A-A截面测量圆监测洞顶的垂直土压力； B-B截面测量圆监测明洞两侧的水平土压力； C-C截面测量圆监测洞顶的颗粒竖向位移。

图2 拱形明洞离散元模型数值模型(单位：m)Fig.2 Discrete element method model for arched cut- and -cover tunnel(unit：m)

在填土过程中，选用黄土作为填料，由于其属于黏性材料，故在颗粒流PFC2D软件分析模型中，颗粒间选择线性接触黏结模型(Linear Contact Bond Model)，颗粒与墙体间选择线性接触模型(Linear Contact Model)。

1.2 细观参数选取

本文涉及的材料有填土材料和减载材料，填土材料选用李盛(2015)所研究的相对压实度R=85%，黏聚力c=31.11kPa，φ=28.24°的黄土。而且，由于其大小(姚玉相等， 2019b)和形态(赵洲等， 2019)对土压力都有影响，故在本文中选取粒径为6～10mm的圆形颗粒来模拟。根据姚玉相等(2019a)的研究，减载材料EPS板高为0.15m、宽为0.30m时减载效果最佳，故本文选此EPS板尺寸进行研究。建模时通过线性接触模型的圆盘(disk)颗粒单元来模拟，其颗粒半径服从标准正态分布曲线。

在参数获取的过程中，为了颗粒集合表现的宏观特性与预设的宏观特性一致，本文建立数值双轴试验模型，通过不断调整颗粒集合的细观参数进行反演算，最终确定本文的细观参数详见表1。

表1 PFC2D颗粒流模型细观参数Table1 Micro-parameters of PFC2D particle flow model

2 矢跨比影响规律分析

为了分析矢跨比对EPS板减载明洞的影响，模型保持边坡坡角β=70°，槽宽比B/D=3.0，分别对矢跨比S/D=0.4、0.5、0.6、0.7、0.8、0.9 6种情况进行数值分析，然后根据图2中布置的测量圆，使用程序自带的测量圆命令，分别对6种不同矢跨比的拱形明洞测量圆位置处的垂直土压力、水平土压力及颗粒竖向位移进行监测和记录，分析其变化规律。同时，使用“等效荷载法”对洞顶范围内平均垂直土压力和明洞侧面平均水平土压力进行分析，并研究洞顶配位数、孔隙率及明洞接触力的大小，最终得到明洞设计的最佳矢跨比。

2.1 土压力分析

2.1.1 垂直土压力分析

由图3可知：EPS减载下，由于EPS板的向下变形，导致内土柱沉降大于外土柱沉降，出现土拱效应，荷载向明洞两侧转移，洞顶受力减小，使得A-A截面处垂直土压力沿水平方向大致呈平缓-增大-减小的趋势。在洞顶范围内(距洞顶左右10cm范围)，当矢跨比在0.4～0.9之间变化时，该截面处垂直土压力随矢跨比的变化几乎不发生变化。在该范围外，垂直土压力变化较为明显，按矢跨比从小到大依次为：0.8、0.9、0.7、0.6、0.5、0.4，并在距洞顶左右各约20cm处不同矢跨比下的垂直土压力达到最大值。

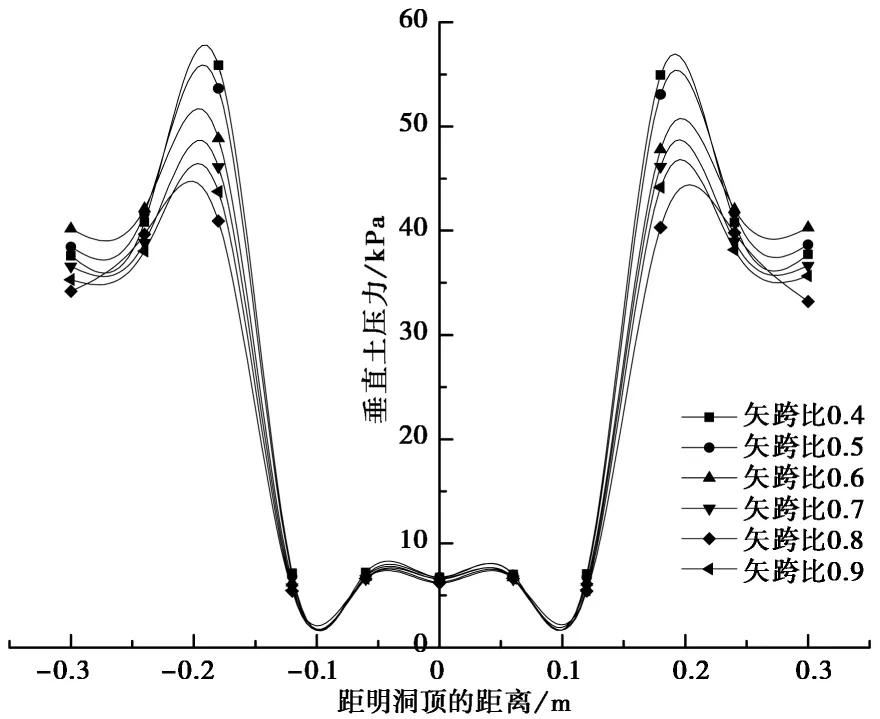
图3 不同矢跨比模型A-A截面处颗粒垂直土压力变化Fig.3 Variations of vertical earth pressure with different height-span ratio models at section A-A

2.1.2 水平土压力分析

由图4可知：B-B截面处水平土压力沿洞壁竖直向上呈增大-减小-增大-减小的趋势。在0.4倍的洞高范围内，水平土压力先略微增大，随后又逐渐减小，在0.4倍洞高处不同矢跨比下的水平土压力几乎达到相等，并在该范围内的水平土压力随矢跨比的增大而减小。在此范围外，当矢跨比0.4时，在0.8倍洞高处达到最大值，随后由于EPS板的减载作用又急剧减小； 当矢跨比在0.5～0.9之间时，在0.9倍洞高处达到最大值随后又不断减小。

图4 不同矢跨比模型B-B截面处颗粒水平土压力变化Fig.4 Variations of horizontal earth pressure with different height-span ratio models at section B-B

使用“等效荷载法”计算的不同矢跨比洞顶范围内平均垂直土压力和明洞侧面平均水平土压力如图5所示。据图分析可知：洞顶范围内平均垂直土压力先减小后增大，在矢跨比0.8时达到最小值6.04kN。明洞侧面平均水平土压力先增加后减小，在矢跨比0.8时达到最大值22.66kN。故认为0.8为EPS减载后明洞的最佳矢跨比。

图5 不同矢跨比模型颗粒平均土压力变化Fig.5 Variations of average earth pressure with different height-span ratio models

2.2 位移分析

当矢跨比在0.4～0.9之间变化时，位移分布云图相似，故此处仅以矢跨比0.8时为例进行说明。由图6可知：随着填土高度的增大颗粒位移逐渐增大。在明洞周围，内土柱沉降小于外土柱沉降，等沉面呈倒“V”形分布。在明洞上方，内土柱沉降大于外土柱沉降，等沉面呈“V”形分布。

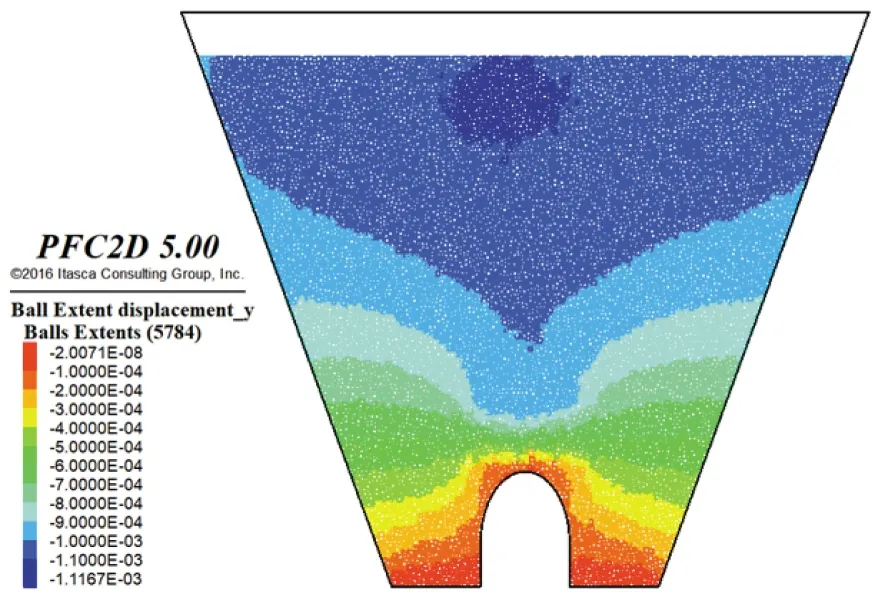
图6 矢跨比0.8颗粒竖向位移云图变化Fig.6 Vertical displacement nephogram of height-span ratio 0.8

为了得到颗粒竖向位移的差异，取不同矢跨比下C-C截面处颗粒竖向位移进行对比，如图7所示，EPS减载下，该截面处颗粒竖向位移呈中间大两头小的变化规律，即明洞轴线处颗粒竖向位移最大，越靠近沟槽壁竖向位移越小，这与图6位移云图的变化规律相吻合。在矢跨比0.4～0.9的范围内，竖向位移按矢跨比从大到小依次为：0.8、0.9、0.7、0.6、0.5、0.4。另外，洞顶范围内相对位移差随矢跨比增大依次为：0.075mm、0.080mm、0.083mm、0.089mm、0.091mm、0.089mm，在矢跨比0.8时达到最大值0.091mm，说明洞顶垂直土压力越小，颗粒相对位移差越大。

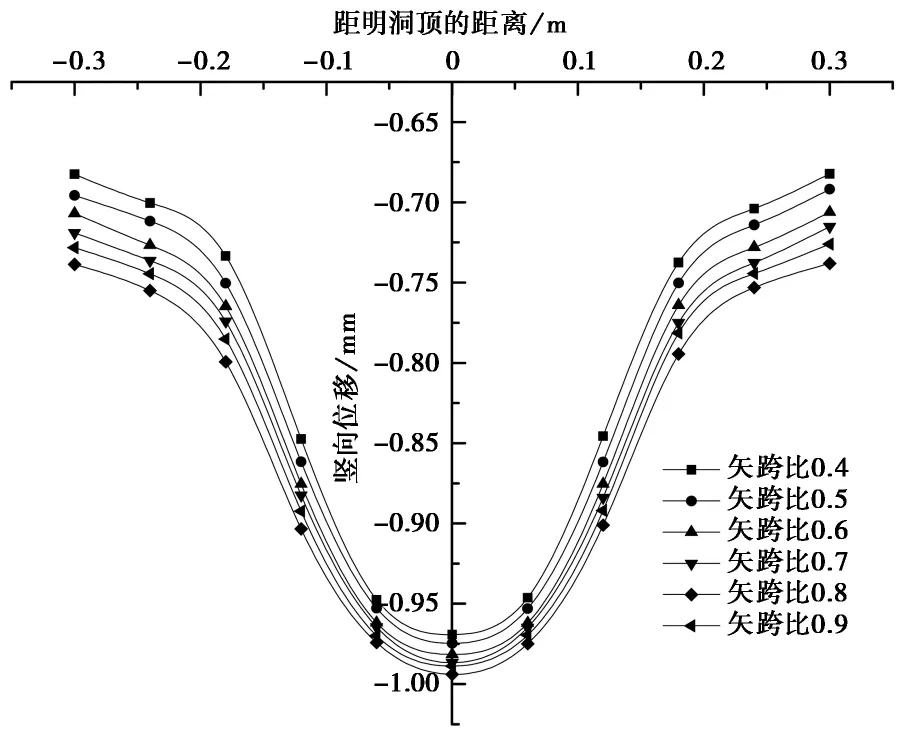
图7 不同矢跨比模型C-C截面处颗粒竖向位移变化Fig.7 Variations of vertical displacement with different height-span ratio models at section C-C

2.3 颗粒间接触分析

2.3.1 配位数与孔隙率分析

配位数是指模型中平均每个颗粒相接触的颗粒数目，是评价一个颗粒体系接触是否良好、密实性好坏的重要指标。孔隙率是指模型中孔隙面积与整个模型面积的比值。由图8可知：明洞顶土颗粒配位数与孔隙率成反比关系，配位数越小，孔隙率越大。在矢跨比0.4～0.8范围内，配位数在不断减小； 在0.8～0.9范围内，配位数逐渐增大，矢跨比0.8时达到最小值4.16。而孔隙率则在矢跨比0.4～0.9范围内先增大后减小，在矢跨比0.8时达到最大值0.147。这与图5所示变化规律相吻合，即平均垂直土压力与配位数成正比，与孔隙率成反比； 平均水平土压力与配位数成反比，与孔隙率成正比。

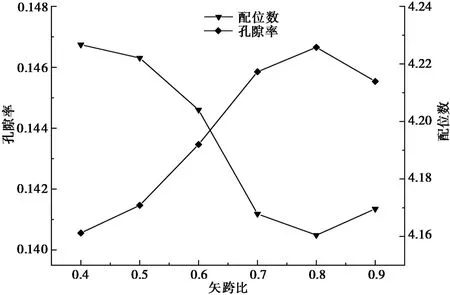
图8 不同矢跨比明洞顶颗粒配位数与孔隙率变化Fig.8 Variations of coordination and porosity on top of cut- and -cover tunnel with different height-span ratios

2.3.2 接触力链分析

接触力的分布实质是土体中荷载传递特征的体现，图中黑线和红线分别表示压力和拉力，出现拉力是因为填土本身就具有黏性，颗粒间存在黏聚力。线的粗细代表接触力的大小，线条组成的网络结构形式代表力的分布和荷载的传递方向。由图9可知：EPS板减载下，力链偏转角较大，明洞土体内部产生明显的土拱，土拱拱脚主要位于明洞两侧洞壁及底部上，并且，明洞两侧的接触力链较明洞顶上方分布更密集，接触线条更粗，颗粒间接触力更大。当矢跨比从0.4增加到0.8时，模型内部接触力链逐渐变得稀疏，接触力逐渐减小； 当矢跨比超过0.8，继续变化到0.9时，模型内部接触力链相较于矢跨比0.8时的接触力链变得稠密，接触力增大。再次说明EPS板减载后明洞存在一个最佳矢跨比0.8。

图9 不同矢跨比颗粒间的接触力链分布Fig.9 Distribution of contact force chain for soil particles with different height-span ratiosa.矢跨比0.4； b.矢跨比0.8； c.矢跨比0.9

3 最佳矢跨比明洞影响因素分析

采用第2节中矢跨比S/D=0.8的离散元模型，通过改变槽宽比B/D(李盛等， 2018b)和边坡坡角β(李伟龙， 2015)的大小，分析洞顶水平面垂直土压力、颗粒竖向位移、明洞侧面水平土压力及颗粒接触的变化规律，从而得到以上各参数在最佳矢跨比下明洞土压力的影响程度。

3.1 槽宽比B/D对土压力的影响

为了研究槽宽比B/D的变化对明洞土压力的影响，模型计算中保持边坡坡角β=70°，通过调整沟槽宽度B来实现槽宽比B/D的不同比例，B/D分别为1.5、2.0、3.0、4.0。

3.1.1 土压力分析

使用“等效荷载法”计算的不同槽宽比洞顶范围内平均垂直土压力和明洞侧面平均水平土压力如图10所示。由于槽宽比越大，边坡对明洞顶土体的约束作用减弱，明洞顶内外土柱之间颗粒的摩擦逐渐减小，楔紧作用变弱，导致随槽宽比的增大，洞顶范围内平均垂直土压力逐渐增大，依次为：6.32kN、6.46kN、6.72kN、6.91kN，明洞侧面平均水平土压力逐渐减小，依次为：25.21kN、24.04kN、21.90kN、19.12kN。

图10 不同槽宽比模型颗粒平均土压力变化Fig.10 Variations of average earth pressure with different ratios of groove width model

3.1.2 位移分析

图11所示为不同槽宽比条件下C-C截面处颗粒竖向位移差的变化规律。由图可知，当槽宽比在1.5～4.0之间变化时，随槽宽比的增大，颗粒竖向位移不断差减小。其大小随槽宽比减小依次为0.087mm、0.078mm、0.075mm、0.074mm。

图11 不同槽宽比模型C-C截面处颗粒竖向位移差变化Fig.11 Variations of vertical displacement difference with different ratios of groove width model at section C-C

3.1.3 配位数与孔隙率分析

如图12所示，随着槽宽比的增大，明洞顶土颗粒配位数减速增大，孔隙率加速减小，这与图10所示平均土压力变化规律相吻合，即平均垂直土压力越大，平均水平土压力越小，配位数就越大，孔隙率就越小。

图12 不同槽宽比明洞顶颗粒配位数与孔隙率变化Fig.12 Variations of coordination and porosity on top of cut- and -cover tunnel with different ratios of groove width

3.2 边坡坡角β对土压力的影响

为了研究边坡坡角变化对明洞土压力的影响，模型计算中保持槽宽比B/D=3，边坡坡角β分别为60°、70°、80°、90°。

3.2.1 土压力分析

使用“等效荷载法”计算的不同边坡坡角洞顶范围内平均垂直土压力和明洞侧面平均水平土压力如图13所示。由于边坡坡角越大，明洞填土量越小，导致垂直土压力随着边坡坡角的增大减速减小，减小率依次为：7.22%、5.71%、2.57%，明洞侧面平均水平土压力减速增大，增长率依次为：46.80%、36.74%、27.26%。

图13 不同边坡坡角模型颗粒平均土压力变化Fig.13 Variations of average earth pressure with different slope angle models

3.2.2 位移分析

由图14可知：不同边坡坡角条件下C-C截面处颗粒竖向位移差随边坡坡角的增大不断增大，其大小随边坡坡角增大依次为0.078mm、0.085mm、0.108mm、0.116mm。

图14 不同边坡坡角模型C-C截面处颗粒竖向位移差变化Fig.14 Variations of vertical displacement difference with different slope angle models at section C-C

3.2.3 颗粒间接触分析

3.2.3.1 配位数与孔隙率分析

如图15所示，随着边坡坡角的增大，明洞顶土颗粒配位数不断减小，孔隙率不断增大，两者互成反比关系，这与图13所示平均土压力变化规律相吻合，即平均垂直土压力越小，平均水平土压力越大，配位数就越小，孔隙率就越大。

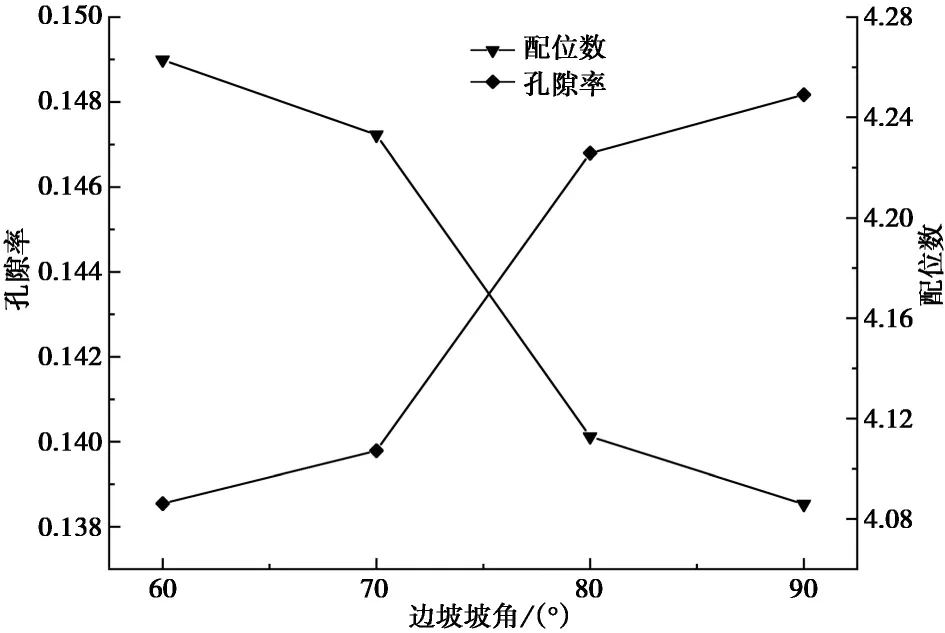
图15 不同边坡坡角明洞顶颗粒配位数与孔隙率变化Fig.15 Variations of coordination and porosity on top of cut- and -cover tunnel with different slope angles

3.2.3.2 接触力链分析

边坡坡角60°和90°下土体颗粒间接触力链的变化如图16所示。由图可知，随着边坡坡角的增大，明洞两侧及高层填土区的接触力链越来越稀疏，土压力逐渐减小，并且边坡坡角越大，接触力链偏转角逐渐减小，当达到90°时接触力垂直于明洞两侧底部。

图16 不同边坡坡角颗粒间的接触力链分布Fig.16 Distribution of contact force chain for soil particles with different slope anglesa.边坡坡角60°； b.边坡坡角90°

4 结 论

针对不同矢跨比拱形明洞，本文利用离散元PFC2D软件进行数值模拟，研究了EPS板减载下不同矢跨比拱形明洞顶垂直土压力、颗粒竖向位移、明洞侧面水平土压力及颗粒间接触的变化规律，进一步明确了不同槽宽比和边坡坡角对最佳矢跨比明洞土压力的影响规律。主要结论如下：

(1)EPS板减载下，拱形明洞各个截面的垂直土压力、水平土压力、竖向位移及接触分布的变化规律不同。洞顶水平面垂直土压力沿洞顶水平方向向两侧呈“U”形变化； 明洞侧面水平土压力沿竖向呈斜“S”形变化； 洞顶水平面颗粒竖向位移沿洞顶水平方向向两侧呈“V”形减小。

(2)当矢跨比在0.4～0.9范围内时，洞顶范围内平均垂直土压力先减小后增大，在0.8时达到最小值6.04kN； 明洞侧面平均水平土压力和洞顶范围内颗粒竖向位移差先增大后减小，在0.8时达到最大值22.66kN、0.091mm； 配位数先减小后增大，孔隙率先增大后减小， 0.8时分别达到最小值、最大值4.16和0.147。

(3)在最佳矢跨比0.8下，减小沟槽宽度、增加边坡坡角，洞顶范围内平均垂直土压力逐渐减小，明洞侧面平均水平土压力逐渐增大，接触力链逐渐变得稀疏。故减小槽宽比、增大边坡坡角，土压力越小，明洞受力越合理。