基于Mamdani FIS的中吉乌铁路方案线中段滑坡易发性预测*

杨晨晨 张 志 崔振昂 夏 真

(①中国地质调查局广州海洋地质调查局， 广州 510700， 中国)(②中国地质大学(武汉)地球物理与空间信息学院， 武汉 430074， 中国)

0 引 言

滑坡易发性预测作为一种对滑坡的空间分布和发生概率进行预测的方法，其预测结果可为滑坡灾害风险管理、滑坡预防监测及工程规划等工作提供重要的科学依据。滑坡易发性预测的方法可根据所依据的理论基础的差异，分为确定性模型和非确定性模型。确定性模型是基于物理知识，将传统的斜坡破坏力计算模型与空间基础信息相结合，对区域滑坡易发性进行预测分析(王志旺等， 2012)。确定性模型需要大量的岩土力学和水文学参数，但是这些参数的值往往会随着采样点空间位置的变化而变化，不适合大范围内的滑坡易发性研究(van Westen et al.，2006)。因此，基于物理特征的确定性模型难以应用于区域滑坡的易发性预测上。

非确定性模型以统计学知识为基础，将影响边坡稳定性的因子按照一定权重叠加，通过统计分析滑坡与其敏感因子之间的关系来预测其易发性。根据对滑坡敏感因子权重取值方法的不同，非确定性模型主要分为以信息量法、逻辑回归、人工神经网络、支持向量机为代表的知识驱动模型和以模糊数学和层次分析法为主的数据驱动模型。张俊等(2016)基于GIS与信息量-快速聚类模型对三峡库区万州区滑坡易发性进行了评价； 樊芷吟等(2018)采用信息量模型、Logistic回归模型以及两种模型耦合对汶川县地质灾害易发性进行评价，结果表明采用耦合模型较信息量或 Logistic 单一模型评价结果更加合理、精度更高； 伍宇明等(2014)基于贝叶斯理论和马尔科夫蒙特卡罗模型构建了小流域滑坡稳定性的优化模型，解决了滑坡稳定性评价中参数难以确定的问题。 Devkota et al.(2013)应用证据权法、确定性系数法、逻辑回归模型方法对尼泊尔Mugling-Narayanghat road 地区的滑坡进行了研究，并将几种方法的预测精度进行对比； Althuwaynee et al.(2014)基于决策树模型对韩国Pohang-Kyeong Joo 流域进行了滑坡易发性预测，并将预测结果与多元逻辑回归模型分析的结果进行了对比； Ayalew et al.(2005)基于逻辑回归模型分别对日本Kakuda-Yahiko 山区和美国Colorado 中西部地区开展了滑坡易发性分析，并将不同研究区内的预测结果进行对比。

知识驱动模型虽然可将模糊的信息进行量化，但是其过分依赖专家的主观经验和知识，这将影响滑坡易发性预测结果的可靠性。以客观数据为基础的数据驱动模型可以有效地削弱其主观性，但是数据驱动模型忽略了专家知识在区域滑坡地质成因与规律方面的作用。而Mamdani模糊推理系统(Mamdani FIS)中既有专家主观意见的参与，但又不完全依赖于专家意见(肖治宇等， 2011)。

与地球科学中常用的统计方法比，模糊推理系统(Mamdani FIS)在解决复杂的地学问题时大大减小结果的不确定性。Grima(2000)认为FIS有如下的优势。

(1)FIS通过使用模糊“if-then”规则明确表达专家知识；

(2)FIS通过专家解决问题的方式来处理主观不确定性(模糊性和不准确性)；

(3)FIS具有一定的数学基础。

虽然该模型在工程地质的研究中有了较为成熟的研究，但是Mamdani模糊推理系统用于滑坡的易发性预测的研究相对较少，应用于道路工程稳定性分析的研究更是少之又少。Akgun et al.(2012)基于Mamdani FIS模型，实现了土耳其北部Sinop 地区及其附近滑坡敏感性评价； 张纫兰等(2014)利用模糊推理模型对三峡库区巴东—秭归研究区内的滑坡进行易发性评价研究； 蒋钰峰等(2019)基于GIS技术，分析对比川藏铁路三江并流区的地形地貌参数，用于山区铁路选线的分区评价。

中吉乌铁路方案线，起自中国南疆铁路喀什站，途经吉尔吉斯斯坦的卡拉苏，终点为乌兹别克斯坦的安集延站，是我国西北地区通往中亚、南欧国家的一条国际通路(余绍淮等， 2012)，是一带一路基础建设的重要组成部分。铁路沿线地质条件复杂，穿越活动构造带，崩塌、滑坡、泥石流等不良地质体发育，冰水沉积物、冰碛物等均可能对铁路的安全造成威胁。因此，利用GIS结合Mamdani FIS模型进行了滑坡易发性预测，并对预测结果进行评估，为铁路选线提供一定建议。

1 研究区概况

中吉乌铁路路线设计方案分南、北两个路线走廊，本文研究区为北线AK53-AK130、南线AK61-AK131段，地理位置如图1。研究区位于天山构造带，区域构造方向呈近东西向展布。铁路方案线横穿NW—SE向的特拉斯—弗加恩斯基(Talas-ferganskiy)断裂带，构造作用强烈。早志留世至早二叠世，除局部泥盆世中有基性火山岩外，主要为碳酸盐岩沉积，相对而言，费尔干纳东部地区岩性不如西部地区稳定。侏罗纪地层主要为粉砂岩、石灰岩和石膏夹层。白垩纪至第四纪地层有少量出露，为碳酸盐岩和碎屑沉积为主，厚度达千米。区内为高原剥蚀侵蚀地貌，沟谷河流遍布。铁路线穿越费尔干纳山脉，地形起伏落差大，年降雪量丰富，常见自然积雪、风吹雪、雪崩等雪灾，此外融雪型洪水、泥石流，山体滑坡和山崩等次生灾害发育。

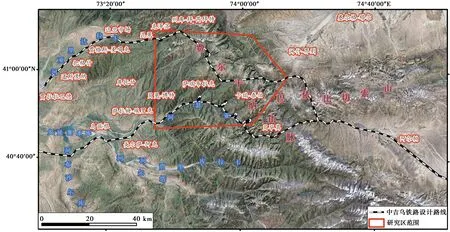
图1 研究区地理位置图Fig.1 Location of the study area

2 Mamdani FIS模型

Mamdani FIS模型是模糊控制中常用的方法，该模型计算过程和推理过程如下所示：

(1)Mamdani FIS的推理过程

Mamdani FIS模型由输入、推理规则if-then语句和输出3部分组成，其具体推理过程如图2所示。

图2 Mamdani FIS推理过程示意图Fig.2 Generalized sketch of the Mamdani FIS structure

(2)Mamdani FIS的计算过程

①将输入对推理规则的隶属度作为参考，对执行程度进行估算。

αi=μAi1(X1)∧μAi2(X2)∧…∧μAin(Xn)

②对每一个规则使用最小值 t-norm 推导其模糊集：

③取最大值作为输出的模糊集

④对模糊集合去模糊化，得到一个离散值。

将Mamdni FIS用于中等尺度的滑坡易发性预测时，采用了若干影响因子进行模糊推理，得到预测结果，之后使用历史滑坡数据对结果进行精度评价。

3 提取滑坡敏感性因子

通过基于地学知识的人机交互遥感调查与实地验证发现研究区内共有滑坡189处，如图3所示。

图3 研究区内历史滑坡点分布图Fig.3 Distribution of historical landslides in the investigation area

控制滑坡发生的因素众多，各因素间相互影响和制约，且对滑坡发生的贡献率不同，故区域滑坡危险性评价时需科学选择参评因素。地层岩性、构造、岸坡结构等因素会对滑坡发育产生一定的作用。李晓等(2008)确定性分析了影响滑坡的相关因素的敏感程度，以此来揭示滑坡的空间分布特征。根据统计分析，在滑坡易发性预测中，影响因子被选取比例最高的是岩性，之后依次是坡度、高程、坡向、断层、人类活动、水系、植被、坡形、降雨因子等(王得双等， 2017)。

除岩性因子外，本文采用单因素方差分析对提出的滑坡因素进行筛选。首先假设单因素方差分析中样本均值相等，分析得到P值和F值，普遍情况下，当P值<0.05时，所作假设被驳回，参与分析的样本可以被区分； 当P值>0.05时，则无法拒绝假设，此时样本不可以被区分。根据单因素方差分析原理，分别选取一定数量的滑坡点与非滑坡点，对两者对应因素值进行比较和方差分析。如果滑坡点与非滑坡点因素方差分析相似性较强，则说明该因素在滑坡与非滑坡特征分析中意义不大，因而在预测中可以忽略其影响(兰恒星等， 2012)。

本文根据研究区概况，从地质环境背景、地形因素和生态环境因素3类滑坡影响因子中选取9种因子。地质环境背景包括岩性、断层和节理，地形因子主要考虑高程、坡度、地面曲率、地形湿度指数(topographic wetness index，TWI)和地表斜坡强度指数(surface slops intensity，SPI)的影响，生态环境因素中只考虑归一化植被指数的作用。

3.1 地质环境背景

3.1.1 地层岩性

前人研究表明，地层岩性与滑坡的发生有着密切的联系。岩石类型、软硬程度及层间结构对岩体机械强度和耐风化能力起着决定性作用，进而影响坡体的稳定性。基于前人研究成果，将岩性分为高易发区、中易发区和低易发区3类，如表1所示。

表1 地层岩性与易发性关系表Table1 Relationships between landslide and lithology

各类岩层中均有滑坡灾害的发育，但是硬岩地层，如花岗岩、碳酸盐岩和砂砾岩等地层中地质灾害最为发育； 软岩地层如泥页岩、千枚岩、砂板岩等地层中地质灾害发育次之(黄润秋等， 2008)。

3.1.2 构造

地质构造的分布情况及规模决定了区域岩体结构面分布情况。岩体稳定性与断裂带分布状况密不可分。断裂带周围地质体完整性较差，断裂带的长期活动发育会使其发生不同程度的位移和形变，进而使得岩体的连续性和稳定性遭到破坏。

研究区构造活动强烈，利用遥感数据解译出区域断裂带1条，一般性断裂235条，活动断裂2条。断裂密度见图4b，分析结果如表2。

图4 研究区各滑坡影响因子示意图Fig.4 Landslide conditioning parameters used in this study

表2 影响因子与滑坡关系表Table2 Relationships between landslide and factor of influence

节理是具有“应力感”的地质构造，同时也是孕育崩塌、滑坡等地质灾害的重要影响因子。区内共解译出节理545条，进行密度分析，见图4c，分析结果如表2。

3.2 地形因素

地形地貌在滑坡的发育过程中起着极为重要的作用，滑坡的空间分布与地形形态和地貌类型有着密切的关系。滑坡与地形之间的关系是可直接识别滑坡并判断其是否可能发生(王恭先等， 2004)。

(1)基于DEM数据，提取了高程信息，见图4d。其中，绝大部分的滑坡集中在海拔3,000 m以下的地区。

(2)一般情况下，坡度对滑坡的发育具有控制作用。在坡度较大的斜坡上，岩土体处于临空状态，稳定性极差，容易产生滑坡； 而在地形起伏不大的山坡，岩土体相对稳定，滑坡不易发生(肖桐等， 2007)。基于研究区DEM数据提取了坡度信息，见图4e。其中，绝大部分的滑坡集中分布在30°～50°范围内。

(3)地面曲率描述的是地形形态，定量的表示地形曲面结构。基于研究区内的DEM数据，提取地面曲率信息，见图4f。

(4)地形控制边坡稳定性，决定土壤湿度和地下水流的空间分布(Yilmaz， 2010)，因此，可通过地形指数来表达土壤湿度指数，地形湿度指数TWI(Topographic Wetness Index)值可通过公式TWI=ln(As/tanβ)获得。式中，As表示地表水在单位长度上所流经的上游区的面积；β表示地形坡度(°)，计算结果见图4g，分析结果如表2。

(5)地表径流强度指数SPI(Stream Power Index)，其值的大小可以定量的表示表面水流潜在的侵蚀能力。值可通过公式SPI=Astanβ获得，计算结果见图4h。

3.3 生态环境因素

植被覆盖度对滑坡发生的可能性有着直接的影响。植被的根茎对坡面具有固结作用，可大幅减少坡面的破坏。一般情况，植被覆盖越高的地方，滑坡发生的可能性越低(李凯等， 2014)。

研究区归一化植被指数由Landsat8遥感影像数据计算获得，见图4 。

4 Mamdani FIS模型的应用

4.1 定义输入、输出变量

本文中将影响滑坡的因子作为输入变量。不同地区的影响滑坡的因子主次不同，因此输入模型之前需对研究区内滑坡影响较大的因子(文海家， 2004)。将前文中选取的9种相关因子作为输入变量，同时将研究区内滑坡易发性分为5个等级，作为输出变量。因此本文中Mamdani FIS模型为一多输入、单输出的模型。

4.2 输入输出变量模糊化

模糊预测之前，先将输入变量中的定性因子地层岩性进行标准化，其他的8个定量因子进行归一化处理后作为输入量，将滑坡易发性输出为5个等级，这样输出和输入的变量的值域都将为[0-1]。将模糊系统中常用的三角隶属函数分配给每个变量。岩性因子的输入设置为3个离散隶属函数，分为高易发区、中易发区、低易发区，其他8个因子均以Min-Max形式的两个隶属函数形式输入。

4.3 建立模糊规则if-then规则库

构建模型的重要内容就是建立模糊规则if-then语句，在该过程中，规则的设定可以将专家知识转化为语言表示，是一个模糊控制的过程。规则建立时，参考专家意见确定了以下7条原则：

(1)在滑坡发生因子中，如果岩性输入为高易发，则滑坡易发性输出为高易发或极高易发；

(2)在滑坡发生因子中，如果岩性输入为低易发，则滑坡易发性输出为极低易发；

(3)除岩性因子外的其他8个因子中，如果有6个及以上因子输入为高，则滑坡易发性输出为极高易发；

(4)除岩性因子外的其他8个因子中，如果有5个因子输入为高， 3个输入为低，则滑坡易发性输出为高易发；

(5)除岩性因子外的其他8个因子中，如果有4个因子输入为高， 4个输入为低，则滑坡易发性输出为中等易发；

(6)除岩性因子外的其他8个因子中，如果有2或3个因子输入为高，其他输入为低，则滑坡易发性输出为低易发；

(7)除岩性因子外的其他8个因子中，如果有1个因子输入为高，其他输入为低，或全部输入为低，则滑坡易发性输出为极低易发；

根据以上原则，本文模型中3类9种因子输入后共产生768条if-then语句，构成了模型中滑坡易发性预测的规则。

5 预测结果及评价

5.1 结果分析

地质环境、地形因素和生态环境因素中的9个因子通过Mamdani FIS模型运算，得到研究区内滑坡易发性预测值。将预测值导入至ArcGIS中得到预测的滑坡易发性指数分布图(图5)。

图5 研究区滑坡易发性指数图Fig.5 Landslide susceptibility index map in the investigation area

为了在视觉效果上更好地区分滑坡易发性程度，将滑坡易发性指数进行重分类成图。分位数、标准差分类、相等间隔、确定间隔和自然间断是常用的栅格数据重分类方法。其中，当数据点的分布具有明显的波谷波峰时，适用自然间断法和分位数法。本文中的滑坡易发性指数分布如图6所示，数据有明显波峰，因此采用自然断点法将分布图重分类为：极高易发区、高易发区、中等易发区、低易发区、极低易发区(图7)。

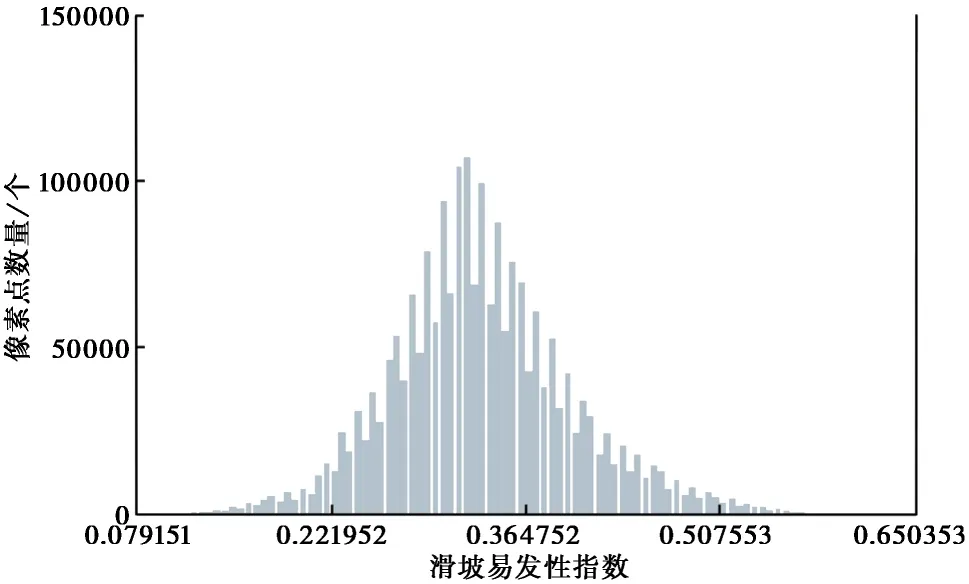
图6 研究区滑坡易发性指数直方图Fig.6 Histogram of the landslide susceptibility index in the investigation area

图7 研究区滑坡易发性指数分级图Fig.7 Landslide susceptibility grading map in the investigation area

极高易发区主要分布在南线AK103-AK131段，和北线AK71-AK78、AK115-AK121段，该地区地质构造极为活跃，且岩性多为片岩，特拉斯—弗加恩斯基(Talas-ferganskiy)断裂带贯穿其中，对其影响较大。铁路穿过极高易发区，而且该区域内存在多处古滑坡，工程施工会破坏其稳定性，对铁路安全造成一定威胁；

高易发区主要分布在南线的AK74-AK102段北侧、北线的费尔干纳山脉东部。费尔干纳山脉东部特拉斯—弗加恩斯基(Talas-ferganskiy)断裂带主干断裂的边缘破碎带、小断层较发育。南线AK74-AK102段位于亚瑟河中游河谷地带，受活动断层影响，地貌不断抬升，河流向源侵蚀加强，使得区域内滑坡等地质灾害有扩大的趋势，对铁路安全有一定影响。

中等易发区主要分布在南线AK81-AK110段南侧以及高易发区外侧区域。南线AK81-AK110段亚瑟河南侧发育多处小滑坡，但是该段铁路线位于河流北侧，河流南侧各种滑坡体对铁路无显著影响。

低易发区和极低易发区主要分布在研究区西部的萨瑞布拉克以及贝曼—博特地区，该区域内海拔较低，地势平缓，构造活动相对较稳定。

根据滑坡易发性预测的结果，统计各个等级下滑坡发生的密度和比率(表3)。由表3可看出，滑坡比率、密度随着易发性等级的增高逐渐增大，易发性等级的空间划分与历史滑坡数据的空间分布情况相符，表明预测划分结果理想，具有一定实践意义。

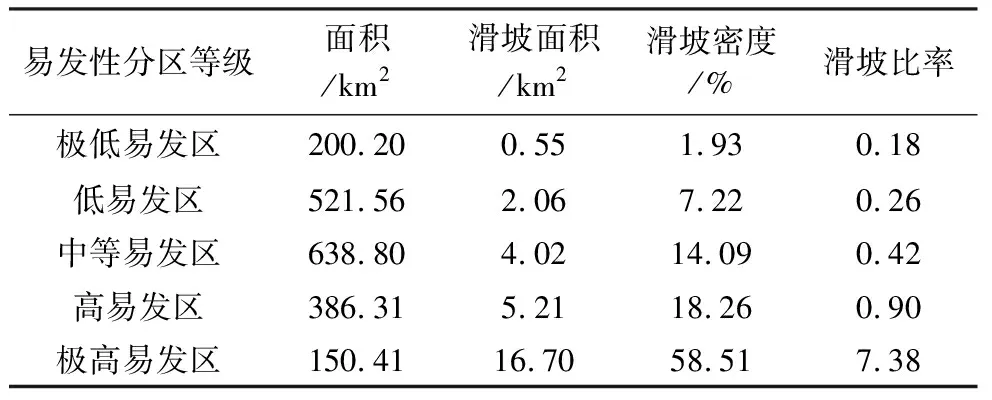
表3 研究区滑坡易发性指数分级统计表Table3 Landslide susceptibility statistics in the investigation area

5.2 精度评价

对模型中滑坡易发性预测结果进行精度评价，以此验证实验模型与预测结果准确性与可信度。利用遥感解译和野外验证获取的滑坡数据作为标准对预测结果进行检验。选取受试者工作特征曲线(Receiver Operating Characteristic Curve， ROC 曲线)进行验证。

选取受试者工作特征曲线(Receiver Operating Characteristic Curve， ROC 曲线)进行验证，该曲线以特异性为横坐标，以灵敏度为纵坐标，且其下方的面积为AUC(area under curve)值可作为准确性评价的指标(李凯等， 2019)。

基于ROC曲线方法，随机选取研究区内800个采样点对滑坡易发性指数进行验证，结果如图8所示，AUC值为0.859，高于张纫兰等(2014)基于Mamdani FIS模型对三峡库区滑坡易发性预测的0.828(张纫兰等， 2014)。与白俊(2013)采用滑坡敏感性系数(CF)分析法对中吉乌铁路沿线滑坡敏感性评价结果对比(白俊， 2013)，分区效果基本一致。可见Mamdani FIS模型对于研究区内滑坡易发性预测具有较高的显著性。

图8 基于ROC的研究区滑坡易发性指数验证图Fig.8 Verification map of landslide susceptibility index in the investigation area based on the ROC

6 结 论

(1)本文结合中吉乌铁路方案线北线AK53-AK130、南线AK61-AK131区段内滑坡的形成条件、影响因素、空间分布特征，选取地质环境、地形和生态环境3个体系中的9个影响因子，基于Mamdani FIS模型获得滑坡易发性等级图，使用ROC曲线对结果验证，得到AUC值为0.859，对于历史滑坡具有较高的诊断作用，因此，该成果可为其他类似工程选址选线提供指导作用。

(2)滑坡极高易发区和高易发区分布在研究区东北部的费尔干纳山脉附近以及南部的亚瑟河流域。南线的AK99-AK131段为研究区的主要滑坡区段，其中部分为古滑坡，滑坡体相对较稳定，但是工程实施后极有可能诱发二次滑坡灾害，而且该区段内的滑坡体松散物为泥石流的发育提供了物源，危险性极大。

(3)本文中研究区滑坡易发性的敏感因子基于GIS和RS技术获取，预测推理模型则参考专家意见构建。该模型可避免繁琐的数据处理过程和大量的野外工作，具有突出的优点。

(4)滑坡易发性预测是多学科交叉的应用，但是在本文中缺少对滑坡机理和诱发机制的分析，且文中没有考虑降雨、人类活动等对滑坡影响的诱发因素，如何。将降雨、人工干扰因素应用于模型，是后期研究中亟待解决的问题。

致 谢衷心感谢王少军教授、张志教授对本文的指导和珍贵的意见，尤其文中模型规则制定中专家意见离不开二位教授等各位专家的指导。在审稿过程中，审稿人对论文的修改提出了翔实具体的修改意见，在此一并表示感谢。