考虑滑床摩擦弱化的大光包滑坡运动机制DDA数值模拟研究*

刘伦杰 富海鹰 张迎宾② 王金梅 王庆栋 相晨琳 程谦恭

(①西南交通大学土木工程学院，成都 610031，中国)(②西南交通大学交通隧道工程教育部重点实验室， 成都 610031，中国)(③西南交通大学地球科学与环境工程学院， 成都 610031，中国)

0 引 言

自公元前780年有地震记载以来(国家地震局震害防御司， 1995)，大量的震害调查结果表明，地震滑坡(Earthquake-induced landslides)常常导致严重的人员伤亡和巨大的财产损失(Keefer， 2002)。2017年8月8日四川九寨沟MS7.0级地震诱发大量山体滑坡，造成了严重的生态破坏，给当地旅游业带来了沉重打击(戴岚欣等， 2017； Fan et al.，2018)。2014年8月3日15时，云南省鲁甸县发生MS6.5级地震，引发了大量的山体滑坡，造成了严重的财产损失(许冲， 2015)。2013年甘肃岷县漳县MS6.6级地震触发滑坡约2300余处(许冲等， 2013a)。2008年汶川发生MS8.0级地震，此次地震触发了大约20万处滑坡，滑坡造成的死亡人数占总伤亡人数的三分之一(Huang et al.，2013； 许冲等， 2013b，2019； 胡厚田等， 2018)。地震滑坡灾害中，大型高速滑坡灾害尤为突出，常表现出体量巨大、速度超快、滑距超远、能量巨大和流动性异常等特点(Huang et al.，2014)，这常常是造成人员伤亡和财产损失的重要原因(汪发武， 2019)。国外关于高速远程滑坡运动机理的研究最早要追溯到1881年Buss和Him研究elm岩崩。在之后的研究中，许多学者对于滑坡的高速机理提出了许多相应的理论，Kent(1966)提出“圈闭空气导致流体化说”； Shreve(1968)提出“气垫层说”； Habib(1975)等学者提出“孔隙水压力说”； 许靖华(K.J.Hsü)(1975)提出“无黏性颗粒流说”； Erisman(1979)提出“岩石自我润滑说”等(沈伟等， 2016)。国内对高速远程滑坡的运动机理研究起步较晚，刘汉超等(1986)认为碎屑间相互碰撞传递的动量是高速远程运动的原因。黄润秋等(1989)认为滑坡高速远程运动是与“滚动摩擦”有关。卢万年(1991)运用“空气动力擎托”进行了定量的分析。总的来说，目前许多学者认为造成高速远程滑坡的原因是摩擦系数的降低。

在高速远程滑坡的研究中，数值模拟是重要的手段。其主要用于获取滑坡的运动距离，堆积范围和厚度等信息，以用于评价高速远程滑坡的危害等。数值模拟主要包括离散介质模型、连续介质模型和耦合模型(沈伟等， 2016)。其中非连续变形分析(DDA)方法(离散介质模型的一种)是石根华博士于1985提出(Shi et al.，1985)，该方法能非常有效地分析非连续块体的失稳破坏过程，并且DDA具有完全运动性特性，严格的平衡要求，正确的能量守恒，因此其能准确地计算高速远程滑坡的全过程。

基于上述优点，许多学者运用DDA研究了大量的高速远程滑坡，如瓦伊昂滑坡(Sitar et al.，1997)和集集地震触发的草岭滑坡(Wu et al.，2011)，汶川地震触发的滑坡(大光包滑坡，东河口滑坡)等(Zhang et al.，2013，2014)。上述文献中在运用DDA研究高速远程滑坡时，整个计算过程很少考虑摩擦力的变化，即摩擦力为常数。然而大量的试验证明了岩石在滑动过程中摩擦系数并非常数(邢爱国等， 2002； Han et al.，2007，2010； Beeler et al.，2008； Dong et al.，2009， 2013)。由此可推知，在大型滑坡中特别是高速远程滑坡中摩擦系数并非常数，而摩擦系数的弱化是导致滑坡高速远程运动的主要原因。因此，在高速远程滑坡的运动机制研究中，有必要考虑滑床摩擦系数的弱化。虽然已有少量学者在研究中考虑了滑床摩擦系数的变化对滑坡运动特征的影响，并获得了一些有益的成果(Lucas et al.，2014； Song et al.，2016)，但鲜有文献将摩擦弱化的具体原因应用于高速远程机制的研究中，尤其在大型地震滑坡的数值模拟研究中更为少见。本文通过Hu et al.(2019)所提供的热分解及动态结晶的现场证据，根据地震中断层间摩擦弱化机制(闪速加热导致热分解及粉末润滑)(Rice， 2006； Han et al.，2010)，对大光包滑坡可能的摩擦弱化机理进行详细的论述。并基于上述摩擦弱化机制及在岩石高速摩擦试验基础上所提出的经验公式(Han et al.，2010)，在DDA中引入摩擦系数随速度变化的摩擦经验公式，用于模拟汶川地震诱发的大光包滑坡在运动过程中摩擦的弱化。

1 大光包滑坡特征及地质背景概况

2008年05月12日，汶川MS8.0级地震触发大量大型高速滑坡，其中大光包滑坡是汶川地震触发规模最大的滑坡，面积约为7.12 km2，估算体积高达11.59×108im3(黄润秋等， 2008，2014； 殷跃平等， 2011； 崔圣华等， 2019)。图1展示了震前大光包的三维地形图，从图中可以看出其陡坡和两翼。结合滑坡处震前的三维地形图及文献可得知大光包从西部到东部的海拔，即最高点大光包的峰顶为海拔大约达到3047 m，最低点为黄洞子山谷海拔约为1450 m(Huang et al.，2012)。大光包山体之上的滑体自高程3047 m溃滑而下后，高速的滑体掠过坡底黄洞子沟，扑向对面的平梁子(顶部高程约2050 m)，滑动距离长达约4.5 km，堆积体宽度达2.2 km，堆积体最大厚度大约达到600 m(Huang et al.，2012)。图2展示了大光包滑坡的轮廓及汶川地震发生前后大光包滑坡沿主滑方向(N60°E)的剖面图(即N60°E滑前和滑后的地形)。

图1 大光包滑坡震前3D地形图(改自Zhang et al.，2013)Fig.1 3D topography model of Daguangbao landslide(Pre-earthquake)(modified from Zhang et al.，2013)

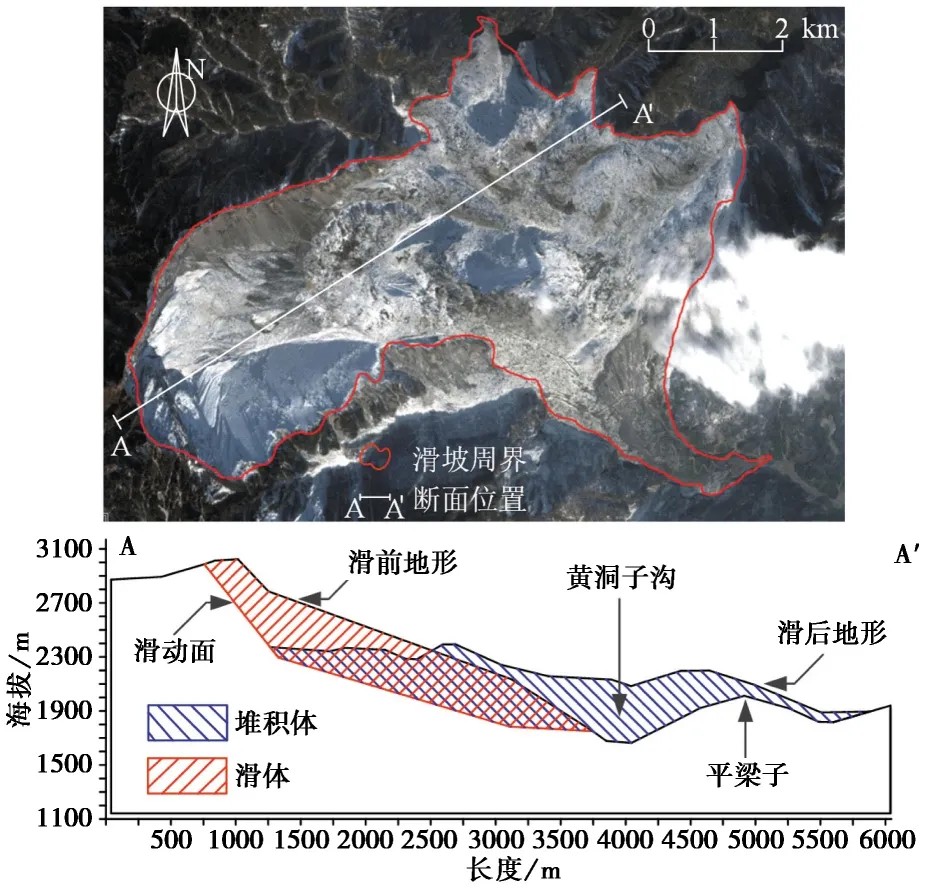
图2 大光包滑坡俯视图及N60°E剖面图(改自Zhang et al.，2013)Fig.2 Image of Daguangbao landslide in bird’s-eye view and profile in N60°E(modified from Zhang et al.，2013)

在3 km的水平方向上高度差约为1600 m(图2和图3)，沿主滑方向上，滑坡地的地形能分为3个部分：第1部分为大光包峰顶，其海拔变化约为2700～3047 m，斜坡的倾角为50°～60°； 第2部分为斜坡中部，其斜坡倾角为30°，海拔高度差约为2000～2700 m； 第3部分海拔高度变化约为1500～2000 m，斜坡倾角为40°～50°(黄润秋等， 2008； Huang et al.，2012)。

图3 大光包滑坡地质平面图及A-A′剖面图(改自Zhang et al.，2013)Fig.3 Geological map of Daguangbao landslide and A-A′ profile(modified from Zhang et al.，2013)

大光包地区的地质图如图3所示。滑坡地区的地层主要包括碳酸盐岩。但其受LMSF断裂带逆冲推覆和长期剥蚀的影响，可将地层主要分为下面几类：(1)飞仙关组(Tf2，Tf1)，紫红色粉砂岩、粉砂质泥岩夹少量介壳灰岩、泥晶灰岩； (2)梁山组(Pl)，阳新组(Py1)和吴家坪组(Pw)，其中主要由灰-深灰色中-厚层含燧石泥晶灰岩和生物碎屑岩等组成； (3)石炭系总长沟组(Cz)，紫红色粉砂岩； (4)泥盆系沙窝子组(Ds)，白云岩夹灰岩； (5)震旦系灯影组(Zd1，Zd2和Zd3)，红色泥岩、灰岩等(黄润秋等， 2008； Huang et al.，2012)。

2 摩擦弱化机制概述

如前所述在高速远程滑坡中，导致摩擦系数减少的机制有很多，但是其不一定能解释在某种条件下的单一滑坡，通过Hu et al.(2019)所提供的热分解及动态结晶的现场证据，本文根据地震学中断层间摩擦弱化机制，应用闪速加热导致热分解形成粉末润滑这一机理来解释大光包滑坡运动过程，并将其引入DDA中进行运动过程的模拟计算。在岩石上的高速滑动试验中证实了地震中摩擦随着滑动速度增加而减弱的特征，导致急剧的速度弱化特征的微观机理是闪速加热。通常两个粗糙块体表面实际的接触只有名义接触的一小部分，因此这微小的接触将产生高应力，滑动将在微接触上摩擦生热。如果滑动足够快，在该条件下能防止传导散热，即接触面在极短的时间内因摩擦生热温度急剧升高，从而导致热效应，如熔融，水蒸发和其他的物理相的转换等，这会降低微接触的局部抗剪强度，在宏观上则表现出摩擦系数随滑动速度的降低(Rice， 2006； Beeler et al.，2008； Goldsby et al.，2011)。由于微观尺度和效应，闪速加热适用于粗糙、不规则或不均匀的表面，因此Lucas et al.(2014)认为其适用于滑坡。De Paola et al.(2011)认为在微接触处达到闪速温度，会激活化学反应，导致颗粒尺寸减小，产生临界流体等，最终导致摩擦系数减小。根据碳酸盐岩的物理化学性质可知，其在高温环境下容易分解，因此在碳酸盐岩的高速摩擦中，微接触接触面的闪速加热是碳酸盐岩摩擦弱化的关键，是激活热分解的起因(Han et al.，2007； De Paola et al.，2011)，热分解之后由于脱碳，白云岩再结晶形成MgO和CaO细小颗粒造成摩擦系数降低(Han et al.，2010； Hu et al.，2019)，滑动过程中摩擦系数在达到稳定时，稳态摩擦系数与速度的经验公式(以下叫速度弱化摩擦经验公式)如下(Han et al.，2010)：

式中：μss为速度为v时的稳态摩擦系数(可近似为有效tanφ′；φ′为有效内摩擦角，基于速度变化的强度参数)；μss，max是小滑移速率下的稳态摩擦系数；μss，min即速度趋于无限大时的稳态摩擦系数；vc是临界速度，速度为0时，μss即为μss，max， 速度趋于无限大时，μss即为μss，min。

3 DDA及摩擦系数修改

3.1 DDA概述

DDA是在块体理论上发展起来的，通过块体间的接触和对单个块体的位移约束形成一个系统通过总平衡方程求解基本未知量(块体形变量)。块体间的接触通过罚方法处理为接触力与其他外力——摩擦力、体积力、惯性力等一同加入总平衡方程中：

式中：kij与fi都是通过最小势能原理求出。kij是6×6的子矩阵，其中子矩阵kii与块体的材料和kij(i不等于j)有关；fi是6×1的子矩阵，是分配给块体i的荷载。di是6×1的子矩阵，是块体i的形变量。

在DDA的接触中采用罚方法和Mohr-Coulomb准则与最大抗拉强度准则来控制块体间的接触，即罚方法用于防止块体之间有嵌入和重叠，Mohr-Coulomb准则与最大抗拉强度准则用于判断块体的接触状态：锁定，滑动，张开。从接触原理可以看出，在DDA中，摩擦力和黏聚力在接触中起着重要的作用。二维DDA中的接触大体可分为3种情况：角对角、角对边和边对边，如图4。边对边的接触可以转换成两个角对边的接触。例如，图4a中，P1P2和P3P4是两条边，它们是接近平行的，边P1P2和P3P4的接触可转换为两个角对边的接触：角P4对边P1P2接触，角P2和P3P4接触。

图4 接触类型Fig.4 Types of contactsa.边对边接触； b.角对角接触； c.角对边接触

块体间的剪切强度由Mohr-Coulomb准则控制。块体间接触力通过罚方法在块体间加刚性弹簧，保证块体间无重叠和嵌入，并且通过“开-闭迭代”保证块体间无张拉。根据法向与切向刚性弹簧的状态，接触状态可以分为3种：

(1)“张开”，即接触力沿边的垂直方向的分量Rn为拉时(Rn=-kndn<=0)。

(2)“滑动”，即接触力的垂直分量Rn是压时，接触力沿进入线的剪切分量Rs足够大已致发生滑动(Rs>Rntanφ+cl)。

(3)“锁定”，即接触力的垂直分量Rn是压且接触力沿进入线的剪切分量Rs小于库仑定律所得的摩擦力(Rs<=Rntanφ+cl)。

注：kn是法向接触弹簧刚度，dn是法向嵌入距离，φ为内摩擦角(在滑动模拟中近似为有效内摩擦角，常强度参数； tanφ近似为摩擦系数)，c是单位距离的黏聚力，l是接触处计算的黏聚长度。

3.2 DDA摩擦系数修改

由上可以看出DDA中其摩擦力保持不变，这对一般的工程问题，其精度已足够，但是对于其他问题，例如高速远程滑坡，摩擦系数并非常数，而此时采用基于库仑定律的DDA进行计算就得不到比较准确的结果。为此，本文基于Han et al.(2010)所提理论及其所提到的经验公式，将其嵌入子程序以解决滑面摩擦系数为常数的问题。

在DDA开始运算远行接触程序时，本文通过DDA的接触算法找到滑块滑动时滑块与基座的接触，当DDA程序在添加摩擦力矩阵时，我们加入速度弱化摩擦经验公式，其算法流程图如图5(图中n2为滑块与基底的接触数)。根据流程图可知，修改后的DDA主要包括三步，即首先根据DDA程序查找出所有接触后，先判断该接触状态是否为滑动，如果不是则继续运行原DDA程序，如果是进入第二步，根据前面所说的根据已找到的滑块滑动时滑块与基座的接触，计算块体间的相对滑动速度后运用速度弱化摩擦经验公式，进行运算后，更新滑块与基座之间的摩擦系数，最后再运行DDA的其他模块。

图5 基于速度的摩擦弱化在DDA程序中的实现流程图Fig.5 Flow chart of velocity-depending frictional weakening in DDA

4 模拟计算

4.1 修改验证

为了验证摩擦系数修改后的DDA程序的有效性、准确性，本文拟采用以下模型进行模拟计算。

验证模型为简单的滑块模型，即由两个块体组成，其几何尺寸如图6(坡角为30°)，可以抽象地模拟简单的滑坡。验证模型主要用于验证修改后DDA的有效性和准确性。本文对DDA程序的修改主要为了模拟计算滑坡过程中滑面上由于闪速加热导致热分解形成粉末润滑造成的摩擦系数降低，为此计算设计验证模型以初步验证修改后DDA的有效性和准确性。选取Han et al.(2010)所提及的卡拉拉大理岩作为本次验证模拟的材料，其物理参数如表1，摩擦弱化参数选择为Han et al.(2010)所述。最终模拟结果如图7。从图7可以看出DDA所计算的摩擦系数基本符合理论计算值，因此修改后的DDA是有效、准确的。

图6 滑块DDA模型Fig.6 DDA model of sliding block

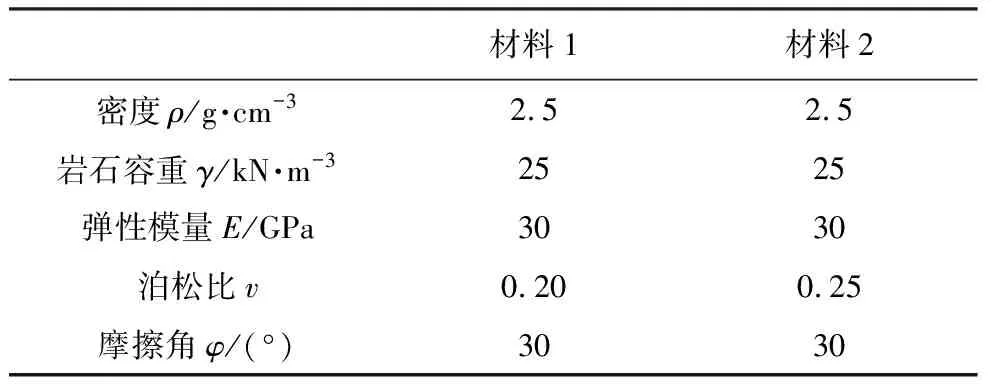
表1 验证模型的物理参数Table1 Physical parameters of materials of verified model

图7 卡拉拉大理岩摩擦系数与速度的关系Fig.7 Friction coefficient of Carrara marble versus sliding velocity

4.2 大光包滑坡模拟

4.2.1 滑坡模型及材料参数

根据第1节图2可知大光包滑坡的主要滑动方向为N60°E，A-A′方向的剖面即为此方向。据此DDA模型选取该方向进行研究，其DDA模型如图8。本文参照殷跃平等(2012)及《工程地质手册》(第五版)，DDA模型中物理参数的选取如表2。

图8 大光包滑坡DDA模型Fig.8 DDA model of Daguangbao landslide

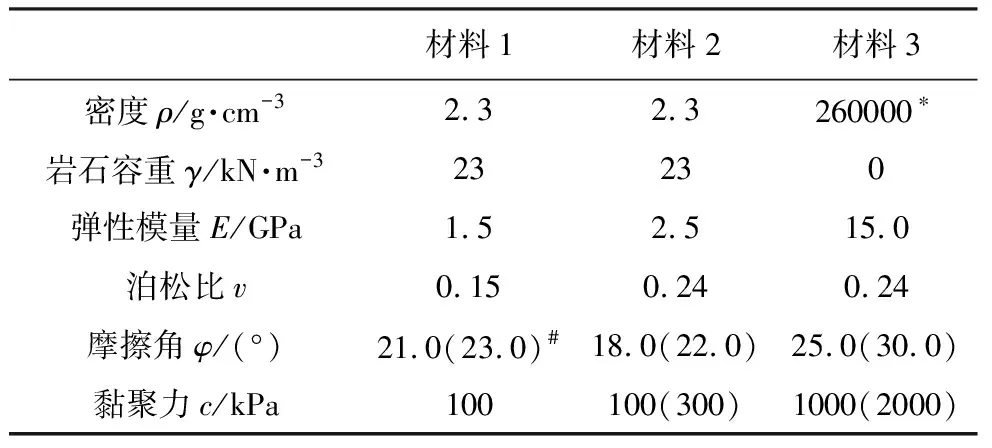
表2 大光包滑坡的物理参数Table2 Physical parameters of materials of Daguangbao landslide

大光包滑坡是汶川地震诱发的最大规模的滑坡，由于大光包滑坡靠近断层，地震动记录的选取必须考虑近断层的特性。Zhang et al.(2015)在地震动记录的选取上提出如下标准：(1)记录地震动的台站必须尽可能的靠近大光包； (2)所选取的地震动记录应尽可能地反映地震动的特性，如由加速度积分产生的残余位移应接近实际地震的残余位移； (3)台站应尽可能地靠近断层。根据上述标准选取中国地震局提供的MZQP台站(注：靠近大光包滑坡与断层的同时，并且能更好的反应地震动特性)所记录的地震动进行校正后作为输入模型的地震动。并将水平地震动(EW，NS)沿主滑方向(N60°E)根据等式a=aE-W×sin60°+aN-S×cos60°(a为水平方向合成地震动，aE-W为MZQP台站记录的EW方向地震动，aN-S为MZQP台站记录的NS方向地震动)进行投影后作为水平方向的输入，垂直方向上的输入则运用MZQP台站的UD方向的记录，输入的地震动如图9。

图9 DDA模拟中输入的地震动时程Fig.9 Inputted ground motion time-histories in DDA simulation

大光包滑坡主要为白云岩，其岩体间的摩擦也主要为白云岩与白云岩之间的摩擦。虽然目前对大多数的碳酸盐的摩擦都集中在断层上，但断层的摩擦与滑坡的摩擦类似(Lucas et al.，2014； Tsao， 2014)。Hu et al.(2019)根据现场证据估计在滑坡高速摩擦时，其温度至少达到了850 ℃； Tsao(2014)在试验中也记录到温度达到了900 ℃。可以得知大光包滑坡在滑动过程中其温度由于闪速加热会迅速达到很高的温度。Hu et al.(2019)通过电子显微镜观察到白云岩的热分解，CO2热液流体穿透细裂缝及矿物的动态再结晶，并且通过高速旋转剪切试验对其进行了证实，因此上文所提弱化机理能用于模拟大光包滑坡的运动过程。为此本文运用文献提供的基于白云岩(来自大光包滑坡)的一系列高速旋转摩擦试验数据进行模拟，其试验数据散点图及运用经验公式拟合图如图10(Dong et al.，2016)。其中，μss，max是小滑移速率下的稳态摩擦系数取0.570，μss，min即速度趋于无限大时的稳态摩擦系数取0.155，vc取为0.2(R2=0.97)。 将拟合后的μss， max，μss， min及vc输入修改后的DDA对大光包滑坡运动过程进行模拟， 并选取滑体前、中、后的块体进行监测(图8中J1、J2、J3)。

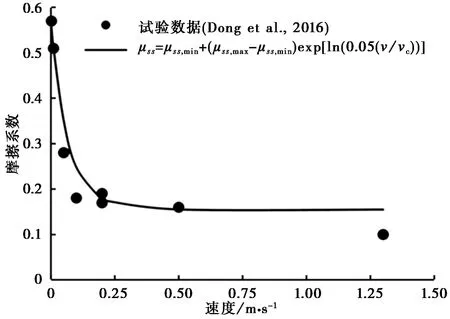
图10 白云岩试验数据散点图及拟合图Fig.10 Dolomite’s scatter plot and fitting plot of dolomite’s test data

4.2.2 结果分析与讨论

本文运用修改前、后的DDA对大光包滑坡运动过程进行模拟，滑坡从稳定到停止时的全过程的模拟结果对比如图11。

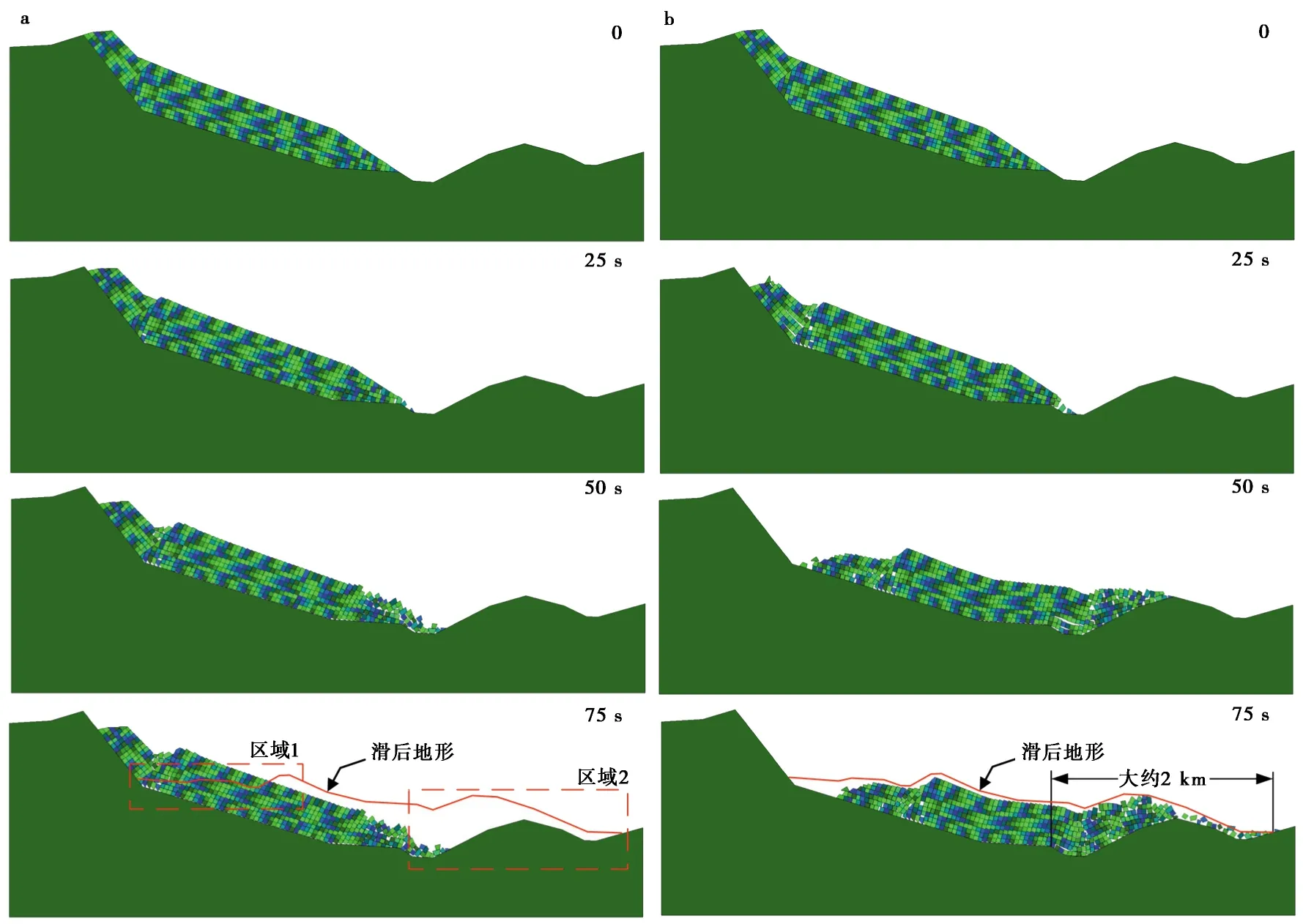
图11 大光包运动过程模拟(参数见表2)Fig.11 Simulation results of Daguangbao landslide(parameters shown in table 2)a.修改前DDA； b.修改后DDA(红实线表示滑坡最终的堆积轮廓)

图11a及图11b分别显示了DDA修改前后的模拟结果，结果表明，DDA模拟的大光包滑坡在到达75 s时基本趋于稳定。图11a中展示了修改前DDA模拟大光包滑坡的全过程，由图中0 s到75 s的结果可以看出大光包滑坡发生后，滑体并没有扑向平梁子，只是堆积在黄洞子沟，这与大光包滑坡野外调查的堆积特征不符(见图11a滑坡最终的堆积轮廓(图中红实线)及图中区域1与区域2(图中矩形红虚线))。而修改后DDA的模拟结果显示(图11b)，滑体掠过黄洞子沟后，大约在50 s左右，爬上对面的平梁子，经紧急制动后(黄润秋等， 2014)，最终形成的堆积形态与野外调查结果基本相符(见图11b滑坡最终的堆积轮廓(图中红实线))。并且前缘滑动距离较修改之前大，达到了约2 km。这也说明大光包滑坡在滑动过程中滑床摩擦系数可能不是常数。

图12显示了监测块体的速度时程，从图中可以看出在地震10 s左右坡体失稳，速度迅速增加，摩擦弱化，这是由于前10 s由于地震动的震荡作用导致坡体内应变能增加，在10 s左右由于应变能累积到一定程度，坡体开始失稳，累计的应变能迅速转换为动能，表现出剧动启程。直观地显示出修改后DDA速度整体大于修改前DDA。在修改前DDA中显示滑坡前缘的速度在10 m·s-1左右，修改后DDA中最大速度达到了约50 m·s-1，与文献中所估计的约45 m·s-1比较接近(黄润秋等， 2014)。在修改后DDA中与平梁子碰撞前(大约35 s)，前缘速度就达到了40 m·s-1，这表明速度弱化摩擦减少了滑动过程中能量的耗散，从全过程堆积形态图(见图11a与图11b中滑坡最终的堆积轮廓(图中红实线))更能说明由于滑动过程中摩擦系数的降低减少了能量的耗散。从修改后DDA速度时间图可以看出在与对面的相反的斜坡相撞后，由于后部滑体提供了大量的动能及未耗散的能量提供给滑体前缘，滑体前缘有明显的二次加速。中部监测块体则未出现明显的速度波动，因为中部监测块体在滑动过程未出现明显与滑体前缘类似的碰撞。从中部监测块体的速度可以看出修改后DDA的速度达到近40 m·s-1，较修改前高。从后部监测块体可以看出修改后DDA的整体速度大于修改前，最大速度也达到了约40 m·s-1。

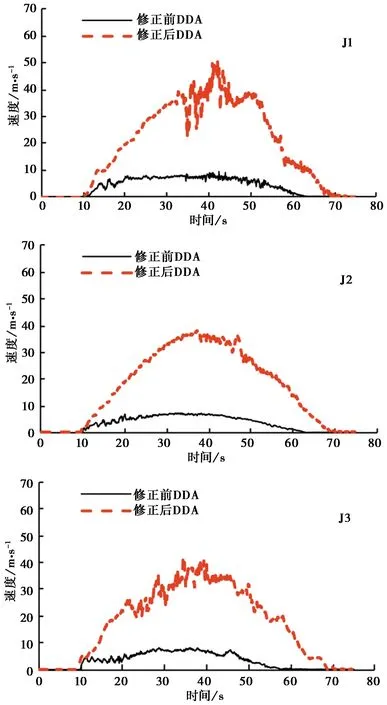
图12 监测点的速度时程Fig.12 Velocity histories of the observation points

图13显示了监测块体的相对位移的时程，修改后DDA在运动到75 s左右时位移基本不变，修改前DDA大约在60 s左右就稳定了(从此可以看出在时间上修改后DDA较修改前DDA滞后)，与修改前DDA相比其位移最终值更大，这也是符合野外测量值的，这也进一步说明大光包滑坡在滑动过程中滑床摩擦系数可能不是恒定的。

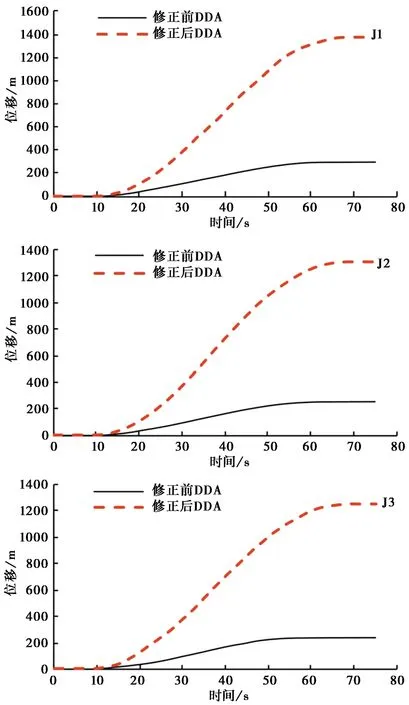
图13 监测点的位移时程Fig.13 Displacement histories of the observation points

当强度参数选取文献(殷跃平等， 2012)里建议范围的另一组值时(表2括号中的数值)，模拟对比结果如图14，从图中可以看出修改前DDA滑动很小，而修改后DDA模拟结果与实际基本相符合。对比修改后DDA对两组强度参数的模拟结果(图11b与图14b)，滑坡的最终堆积形态均与野外地质调查的实际形态非常接近，表明初始强度参数(滑体内的摩擦角及黏聚力)对滑坡的运动特征影响不大，而滑坡运动过程中滑床摩擦系数的弱化可能才是导致大光包滑坡高速远程运动的主要原因。

图14 大光包运动过程模拟(参数见表2)Fig.14 Simulation results of Daguangbao landslide(parameters shown in table 2)a.修改前DDA； b.修改后DDA(红实线表示滑坡最终的堆积轮廓)

5 结 论

本文通过Hu et al.(2019)所提供的热分解及动态结晶的现场证据，根据地震学中断层间摩擦弱化机制，应用闪速加热导致热分解形成粉末润滑这一机理来解释大光包滑坡的高速远程运动过程。并通过修改DDA程序中强度参数的输入方式，以基于速度变化的强度参数取代原DDA程序中的常数强度参数，实现了摩擦系数随接触两侧相对速度变化的动态调整，将修改后的DDA运用于大光包滑坡的模拟，结果表明：

(1)与原DDA相比，修改后的DDA由于考虑了滑床摩擦弱化能够更加合理地模拟滑坡的高速远程运动特征。

(2)与原DDA相比，修改后的DDA对大光包滑坡的模拟结果显示：滑坡在地震作用下失稳后，由于滑床摩擦弱化，更多的能量转化为动能，高速滑体掠过黄洞子沟后，爬上对面的平梁子，最终由于平梁子的“急刹车”作用，滑体停止运动。

(3)与原DDA相比，修改后的DDA对大光包滑坡运动过程和最终堆积形态的模拟结果与已有文献记载和野外调查结果相吻合。这也间接证明了大光包滑坡滑动过程中由于白云岩间摩擦闪速加热导致热分解及粉末润滑造成的摩擦系数降低，可能是造成大光包滑坡高速远程运动特征的重要原因。