无轴承同步磁阻电机最小二乘法转子位移自检测策略

张汉年，张 涛

(1. 南京信息职业技术学院 电子信息学院，南京 210023； 2. 淮阴工学院 自动化学院，江苏 淮安 223003)

0 引 言

无轴承(磁悬浮)电机突破了机械轴承支承的电机无法高速和超高速长时间运行这一瓶颈，也解决了电磁轴承支承的电机体积庞大等缺陷，实现了交流电机转子悬浮和旋转的集成化协同运行[1]。无轴承同步磁阻电机与普通型同步磁阻电机的不同点在于其定子铁心中按照设计要求放置极对数差为1的两套绕组：悬浮绕组和转矩绕组。与轴向叠片各向异性(ALA)、横向叠片(TLA)、永磁辅助型等其他结构类型的转子相比[2]，单一凸极转子无轴承同步磁阻电机制造工艺更为简单、成本优势明显、转子机械强度高，在高速运行、温差大等传动领域有着显著的优势。

要实现无轴承同步磁阻电机的高精度悬浮控制，必须根据转子悬浮状态实时调节悬浮力的大小，首要的是要引入转子径向位移反馈。无轴承同步磁阻电机需要在电机端盖上加装四个高性能电涡流位移传感器来检测转子径向位置，但由此带来一些问题：传感器检测系统复杂且价格昂贵、恶劣环境下传感器检测精度下降、传感器安装和维护难度大等。如果不用复杂且昂贵的位移传感器，只依据电机端电压和电流信号就能在线辨识位移信号进行转子位置闭环控制，将会给无轴承同步磁阻电机悬浮系统的工程设计及应用带来诸多益处。

在无轴承同步磁阻电机转子位移的估算和无位移传感器控制环节，不少学者进行了大量的研究，提出了很多典型的转子位移估算方法。文献[3]将模型参考自适应法应用到电机无位移传感器控制中，但模型参考自适应观测器对固有参数变化较为敏感，降低了系统的稳定性。文献[4]介绍了一种电机转矩绕组高频电压信号注入的转子位置信号提取方法，但对信号处理的技术要求很高。文献[5]通过建立电机精确的电感矩阵模型，导出转子位移与绕组电感之间的关系，但该方法受电机电感参数变化影响较大。最小二乘法可以解决交流电机定子电阻、电感以及转速等参数在线辨识问题，文献[6]将最小二乘法应用于永磁型无轴承电机电感参数的在线估计。本文采用最小二乘法对无轴承同步磁阻电机转子位移进行辨识，所提算法的有效性在仿真实验中得到了证明，实现了电机转子径向两自由度位移量的准确自检测。

1 电机最小二乘法转子位移自检测系统

1.1 最小二乘法位移自检测模型

无轴承同步磁阻电机在d、q坐标系下转矩绕组和悬浮绕组的磁链为

(1)

式中，ψ1d、ψ1q为d、q轴转矩绕组磁链，ψ2d、ψ2q为d、q轴悬浮绕组磁链，i1d、i1q为d、q轴转矩绕组电流，i2d、i2q为d、q轴悬浮绕组电流，L1d、L1q为d、q轴转矩绕组电感，L2d、L2q为d、q轴悬浮绕组电感(悬浮绕组不产生电磁转矩，该绕组对称分布，故L2d=L2q)，x、y为d、q轴转子径向位移，K1m、K2m为电机d、q轴悬浮力-电流转换常数[7]。其中常数K1m、K2m与凸极转子极弧(文中样机为30°)、电机铁心长度、绕组匝数和气隙长度等参数有关，由样机参数，K1m、K2m的估计值分别为60 N/A、26 N/A。

依据式(1)电机磁链方程，忽略电机定子绕组电阻压降和转子偏心位移引起的各绕组互感变化，可得如下电压方程

式中，u1d、u1q为d、q轴转矩绕组电压，u2d、u2q为d、q轴悬浮绕组电压，ω为机械角速度，d/dt为微分算子。

依据式(2)，可得以定子电流为状态变量的无轴承同步磁阻电机状态方程

(3)

其中，

在系统采样周期足够小的情况下，对式(3)进行离散化处理得

(4)

式中，i1d(t+1)、i1q(t+1)、i2d(t+1)、i2q(t+1)为t+1时刻d、q轴转矩绕组和悬浮绕组电流采样值，i1d(t)、i1q(t)、i2d(t)、i2q(t)为t时刻d、q轴转矩绕组和悬浮绕组电流采样值，u1d(t)、u1q(t)、u2d(t)、u2q(t)为t时刻d、q轴转矩绕组和悬浮绕组电压采样值。

假定Ts为系统采样周期，式(4)中，

依据最小二乘算法，直接令矩阵Θ、Y、Z如下

Y=[i1d(t+1)i1q(t+1)i2d(t+1)i2q(t+1)]T

Z=[i1d(t)i1q(t)i2d(t)i2q(t)u1d(t)u1q(t)u2d(t)u2q(t)]T

式(4)可改写成最小二乘法估计模型如下

Y=ΘZ

(5)

式中，Y为输出矩阵，Θ为辨识矩阵，Z为输入矩阵。

(6)

1.2 最小二乘转子位移估计算法

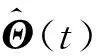
(7)

(8)

无轴承同步磁阻电机在两相静止α、β轴坐标系下，转矩绕组定子磁链分量ψ1α、ψ1β可采用如下估计模型

(9)

式中，u1α、u1β为α、β轴转矩绕组电压，i1α、i1β为α、β轴转矩绕组电流，R1s为转矩绕组定子电阻。

在d、q坐标系下，考虑两垂直方向转子所受径向扰动力Frd、Frq(含重量mg)，以及转子偏离中心位置时受到的不平衡单边磁拉力Fld、Flq，可得转子动态悬浮下的力学模型为

(10)

式中，Fld=kmx、Flq=kmy，其中km为单边磁拉力-位移常数[9]，它与电机的固有结构、气隙磁通密度、铁心长度、气隙长度等参数有关[10]。此处经估算，km=351 N/mm。

2 转速和转矩控制系统

无轴承同步磁阻电机转速和转矩控制由转矩绕组实现，其控制策略与普通同步磁阻电机相同，d、q坐标系下转速及转矩模型为

(11)

式中，pn为转矩绕组极对数，J为转动惯量，Tem为电磁转矩，TL为负载转矩。

3 系统仿真及实验

3.1 控制系统仿真

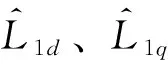
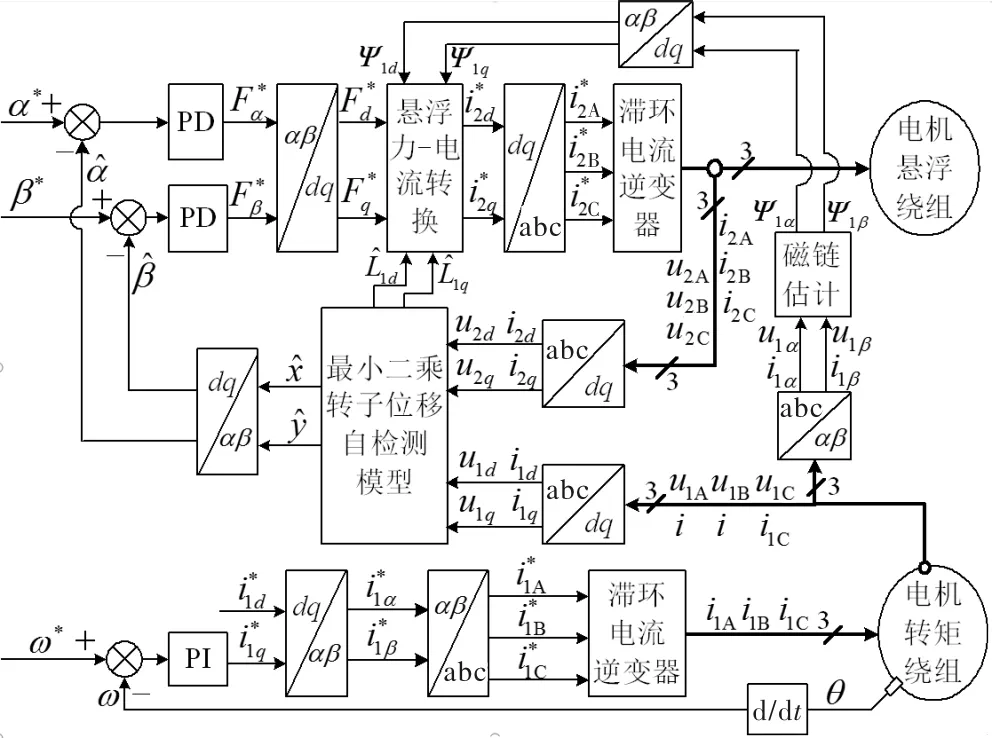
图1 最小二乘法转子位移自检测系统框图

基于图1，搭建无轴承同步磁阻电机最小二乘法转子位置自检测系统仿真模型，进行系统仿真研究，样机主要参数如表1所示。

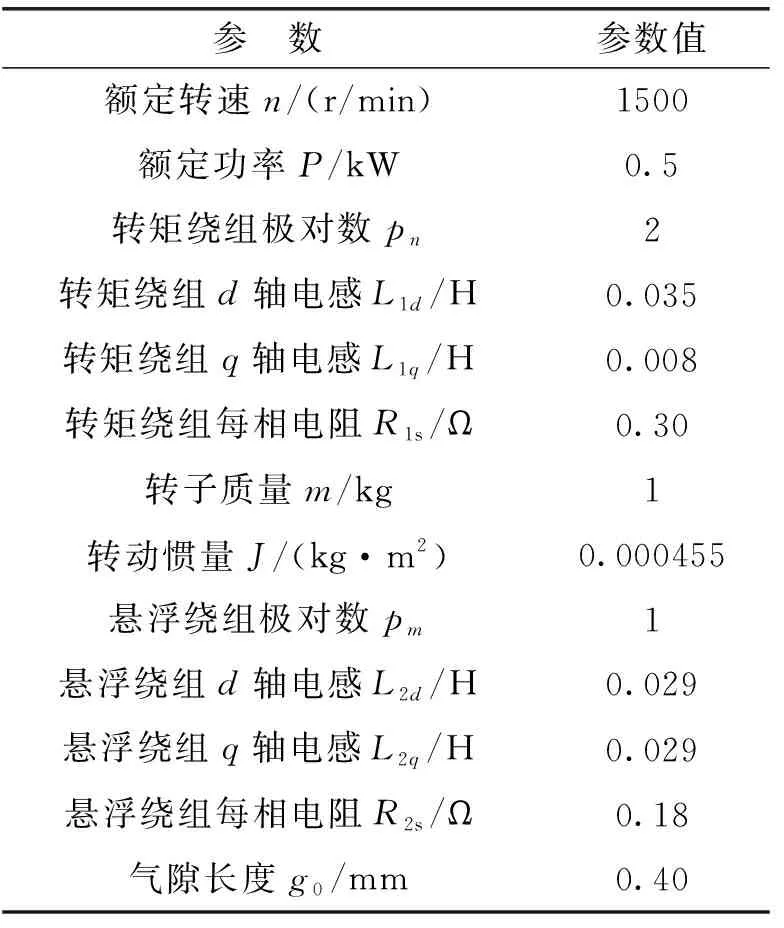
表1 无轴承同步磁阻电机参数

图2给出了样机转速动态突变过程及转子α轴径向位移比较曲线(过程中始终施加2 Nm的负载转矩)，电机转速的动态调节过程如图2(a)所示，初始转速设定为2500 r/min，到0.1 s时目标值降至1500 r/min，再到0.16 s时突增为2000 r/min。上述转速动态过程中同步开展转子位移自检测系统的仿真研究，仿真分别在传统位移传感器法和最小二乘法两种工况下进行，两种工况下转子 轴方向的起动位置均为α=-0.3 mm，如图2(b)所示，最小二乘法比传感器法的位移偏移量动态调节时间稍长，但位移最大波动幅值未超过±0.2 mm，且能在0.1 s内快速悬浮于设定的α=0位置。因β轴转子位移变化规律与α轴基本相同，此处仅给出α轴位移曲线。

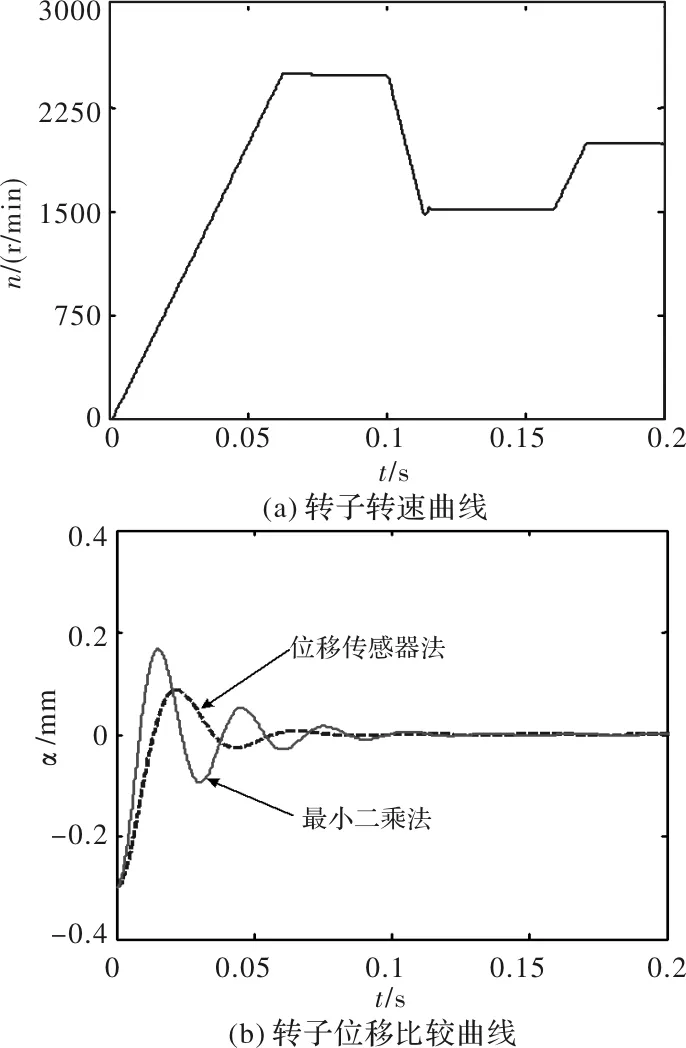
图2 转速调节过程仿真

图3为电机负载转矩变化过程及转子运动曲线(过程中转速恒定为2500 r/min)，图3(a)中转矩的动态过程设定为：0.12 s时电机由空载施加2 Nm负载转矩，到0.15 s时，负载扰动增加为2.8 Nm。上述过程中转子位置坐标以定子中心为原点，由图3(b)可知，在α、β轴方向转子初始偏心坐标为(0.3, -0.25)，目标位置设定为(0, 0)。电机转矩的突然减增对转子运动影响甚小，转子作顺时针方向振动并准确收敛至原点位置，转子位移自检测系统性能较佳。

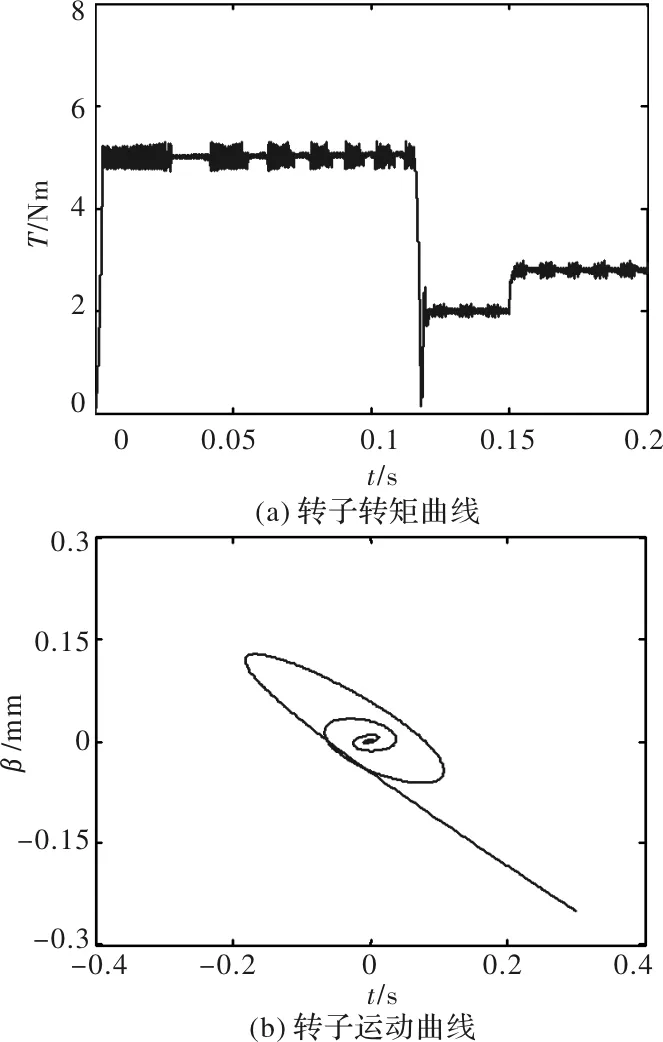
图3 转矩调节过程仿真

3.2 实验分析

图4给出了无轴承同步磁阻电机结构原理图，样机结构为两个自由度，转轴一端(固定端)连接调心球轴承，另一端(悬浮端)可以径向偏移。为避免非悬浮运行时电机转子碰擦定子绕组，转轴悬浮端安装安全备用轴承作防护性支承。测量基准环装配在转轴悬浮端，用于位移传感器精准测量转子径向位置偏移量。

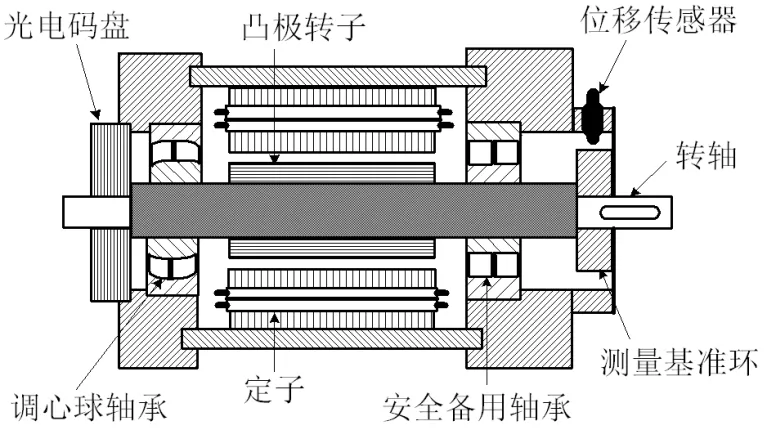
图4 样机结构原理图

图5给出了电机在额定转速1500 r/min稳态运行时沿α、β方向的转轴位移变化情况。由图发现，转轴在α、β方向的径向脉动范围始终在±125 μm以内,表明电机转轴悬浮端已经脱离了安全备用轴承的物理支承，证实了电机转子已处于平稳悬浮与旋转状态。

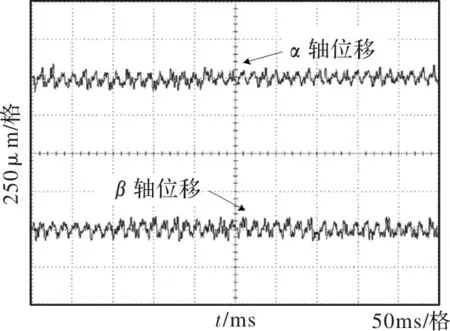
图5 电机稳态运行转子位移曲线

4 结 语

精确的转子位移参数测量是实现高品质悬浮控制性能的前提，针对无轴承同步磁阻电机转子受控悬浮需要安装四个高灵敏度、高价格位移传感器这一难题，设计了该电机最小二乘法转子径向两自由度位置自检测系统。该系统无需传统高精度位移传感器，通过对电机绕组磁链、电压和电流状态方程的变换推导，构建了最小二乘法位移在线估计模型，利用递推最小二乘法对电机的转子位移进行实时辨识。仿真实验证实了该方法的有效性，系统具有良好的稳态悬浮性能和较好的位移量检测精度。